The Prandtl number is a dimensionless similarity parameter to describe the transport of heat and momentum.
Definition
In the article on the different boundary layers, the importance of these boundary layers with respect to heat and mass transfer has already been discussed in more detail. Especially the transport of momentum within the hydrodynamic boundary layer influences the heat transport in the thermal boundary layer. Both transport processes are therefore of decisive importance for the entire heat transfer between wall and fluid.
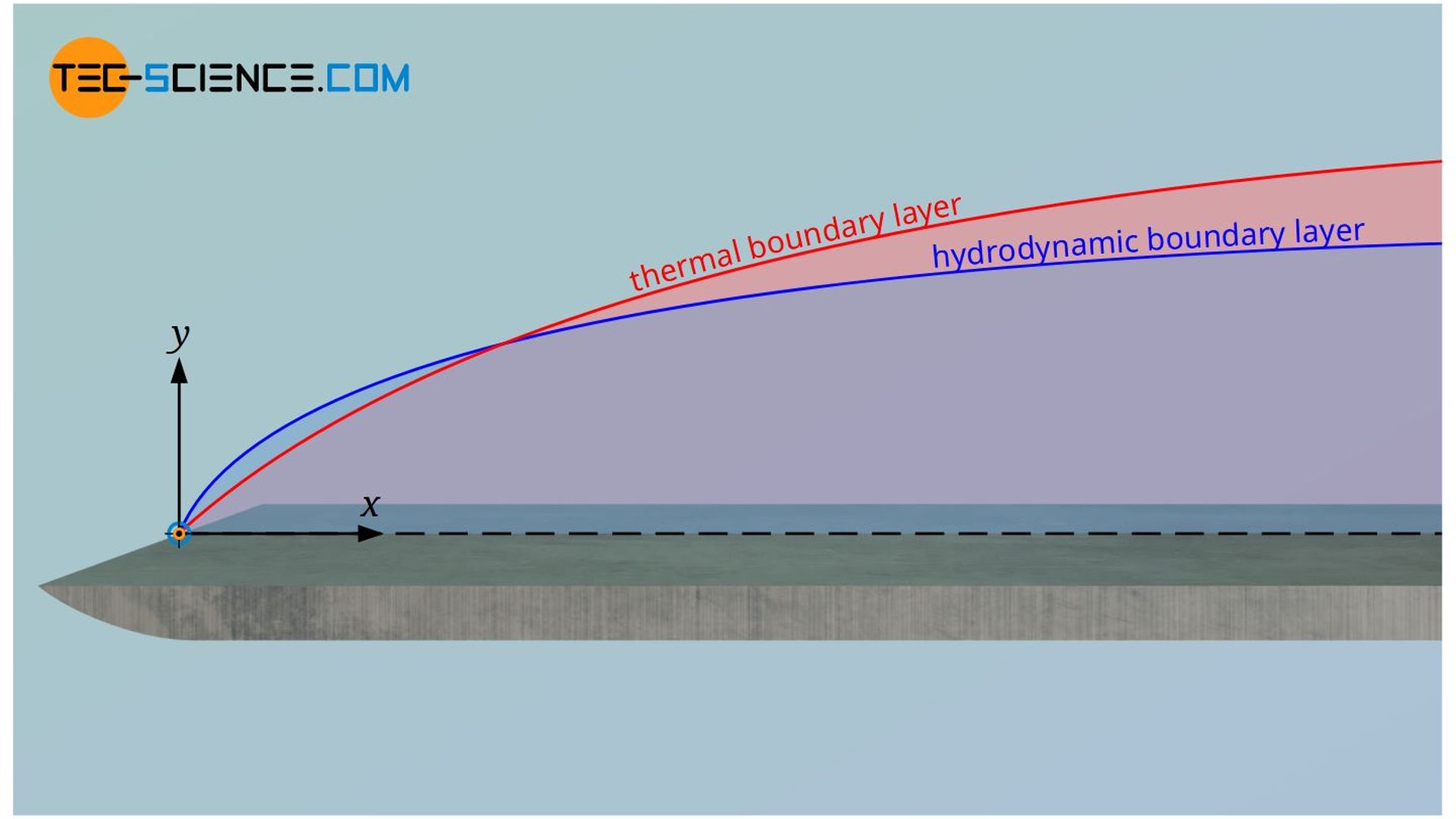
The ratio of the thickness between the velocity boundary layer and the temperature boundary layer is reflected in the so-called Prandtl number. The dimensionless Prandtl number Pr is defined as the ratio of momentum transport (expressed by the kinematic viscosity ν) and energy transport by thermal conduction (expressed by the thermal diffusivity “a”):
\begin{align}
&\text{Prandtl number} = \frac{\text{transport of momentum}}{\text{transport of heat energy}} \\[5px]
\label{pr}
&\boxed{Pr = \frac{\nu}{a}} \\[5px]
\end{align}
The kinematic viscosity ν can also be expressed by the quotient of dynamic viscosity η and density ϱ of the fluid (ν=η/ϱ). The thermal diffusivity “a” in turn can be expressed by the thermal conductivity λ, the density ϱ and by the specific heat capacity cp [a=λ/(cp⋅ϱ)]. The Prandtl number can thus also be determined as follows:
\begin{align}
\require{cancel}
&Pr = \frac{\nu}{a} =\frac{\eta \cdot c_p \bcancel{\rho}}{\bcancel{\rho} \cdot \lambda} \\[5px]
&\boxed{Pr = \frac{\eta \cdot c_p}{\lambda}} \\[5px]
\end{align}
For Prandtl numbers greater than 1, the transport of momentum dominates over heat transfer by thermal conduction. In this case, the velocity boundary layer is larger than the thermal boundary layer. For gaseous water (“steam”) with a relatively low thermal conductivity, both boundary layers are approximately the same size. In this case the Prandtl number is about 1.
Since the quantities contained in the formulas for determining the Prandtl number generally depend on temperature and pressure, the Prandtl number is influenced by both temperature and pressure. For gases, however, the temperature dependence is relatively small and the Prandtl number can usually be considered independent of temperature.
Importance of the Prandtl number for technical practice
At this point one can already see the practical significance of the Prandtl number. If one investigates the convective heat transport of a flowing fluid in a laboratory on a reduced scale, the knowledge gained can only be applied to the real scale if the Prandtl number is identical. This ensures that transport of momentum and energy take place to the same extent. In this case one can therefore assume similar conditions for heat transport.
One can also imagine a heated pipe that transfers heat to a fluid flowing. In this context, the Prandtl number describes how well heat is conducted through the fluid at the pipe wall and transported away by the flow. This is decisive for the entire convective heat transfer. Therefore, the Prandtl number (besides the Reynolds number) is of special importance for the calculation of the Nusselt number, which describes convective heat transfer.
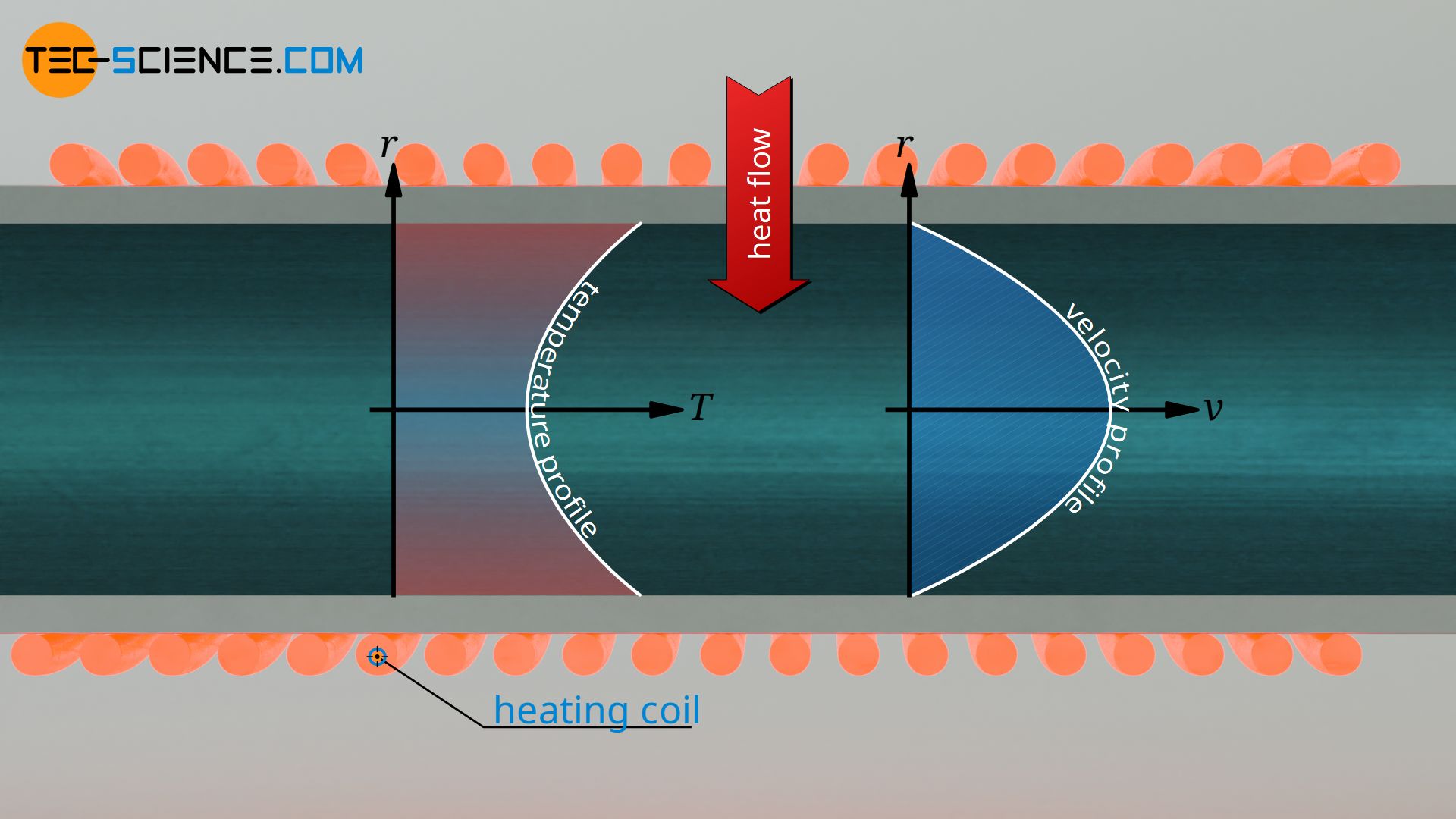
The Prandtl number is a dimensionless similarity parameter which describes heat and momentum transport. Only with identical Prandtl numbers, physically similar heat and momentum fluxes are obtained regardless of the size of the system.
Due to the very good thermal conductivity of metals, the thermal boundary layer of liquid metal as a fluid is usually thicker than the hydrodynamic boundary layer. The heat penetrates, so to speak, very strongly into the flow and therefore leads to a relatively large thermal boundary layer compared to the velocity boundary layer. The Prandtl number therefore approaches zero for liquid metals. Mercury, for example, only has a Prandtl number of 0.023 at room temperature.
For oils with increased viscosity, however, the hydrodynamic boundary layer is thicker than the thermal boundary layer. The relatively low thermal conductivity results in heat not penetrating the flow as strongly. At the same time, the high viscosity of the oil influences the flow over a wide range, i.e. a relatively large hydrodynamic boundary layer is formed. In these cases the Prandtl numbers are significantly higher than 1, e.g. glycerine, which is highly viscous at room temperature, has a Prandtl number of over 11,000. However, the Prandtl number decreases with increasing temperature due to the associated decrease in viscosity.
Péclet number
In practice, one often has to deal with pipe flows that are used for cooling or heating. The aim is to transfer as much heat as possible from the wall to the fluid (or vice versa). In this context the question arises whether large or small Prandtl numbers are advantageous.
Let us consider a flow in a pipe that is heated from outside. According to Fourier’s law of thermal conduction, a large heat flux between wall and fluid is obtained when the temperature gradient at the wall is very high.
Fluids that have a high thermal conductivity would, however, diffuse the heat very quickly in the fluid. This in turn would lead to the fluid having a uniform temperature across the entire pipe cross-section in extreme cases. In the case of high thermal diffusivity, the temperature of the fluid would therefore quickly adapt to the temperature of the pipe wall. However, there would then no longer be a drop in temperature at the wall and the heat flux would come to a standstill between the wall and the pipe.
A high thermal diffusivity therefore leads to a low heat transfer. Conversely, this means that low thermal diffusivity leads to large heat flows, since such fluids have a higher temperature gradient at the wall. According to the equation (\ref{pr}), low values of thermal diffusivity mean high Prandtl numbers. High Prandtl numbers are therefore advantageous for high convective heat transfers.
The temperature gradient on the wall is therefore always the decisive factor for the convective heat transfer. However, it is also influenced by the flow velocity. For Newtonian fluids a parabolic velocity profile is developed inside the pipe (see Hagen-Poiseuille equation). The higher the mean flow velocity, the faster the heat that has penetrated the fluid is transported away. The heat accumulates less at the wall, so to speak, which in turn leads to a greater temperature gradient. High flow velocities therefore also favor convective heat transfer. Since the flow velocity can be expressed by the Reynolds number, the following statement is valid:
High Prandtl numbers and high Reynolds numbers favor convective heat transport!
Thus, the product of Prandtl number and Reynolds number is a measure of the magnitude of convective heat transfer. Therefore a new dimensionless quantity can be defined, the so-called Péclet-number Pe:
\begin{align}
\require{cancel}
\label{pe}
&\boxed{Pe:= Pr \cdot Re}=\frac{\bcancel{\nu}}{a} \cdot \frac{v \cdot L}{\bcancel{\nu}} \\[5px]
&\boxed{Pe= \frac{v \cdot L}{a}} \\[5px]
\end{align}
In this formula, L denotes the characteristic length of the system, e.g. the diameter of a pipe or length of a plate. The Péclet number is a dimensionless similarity parameter which describes the ratio between momentum flux and heat diffusion. As already explained, the Péclet number has a significant influence on convective heat transfer in pipe flows (see article Calculation of Nusselt numbers).
Formula for the calculation of the Prandtl number for air and water
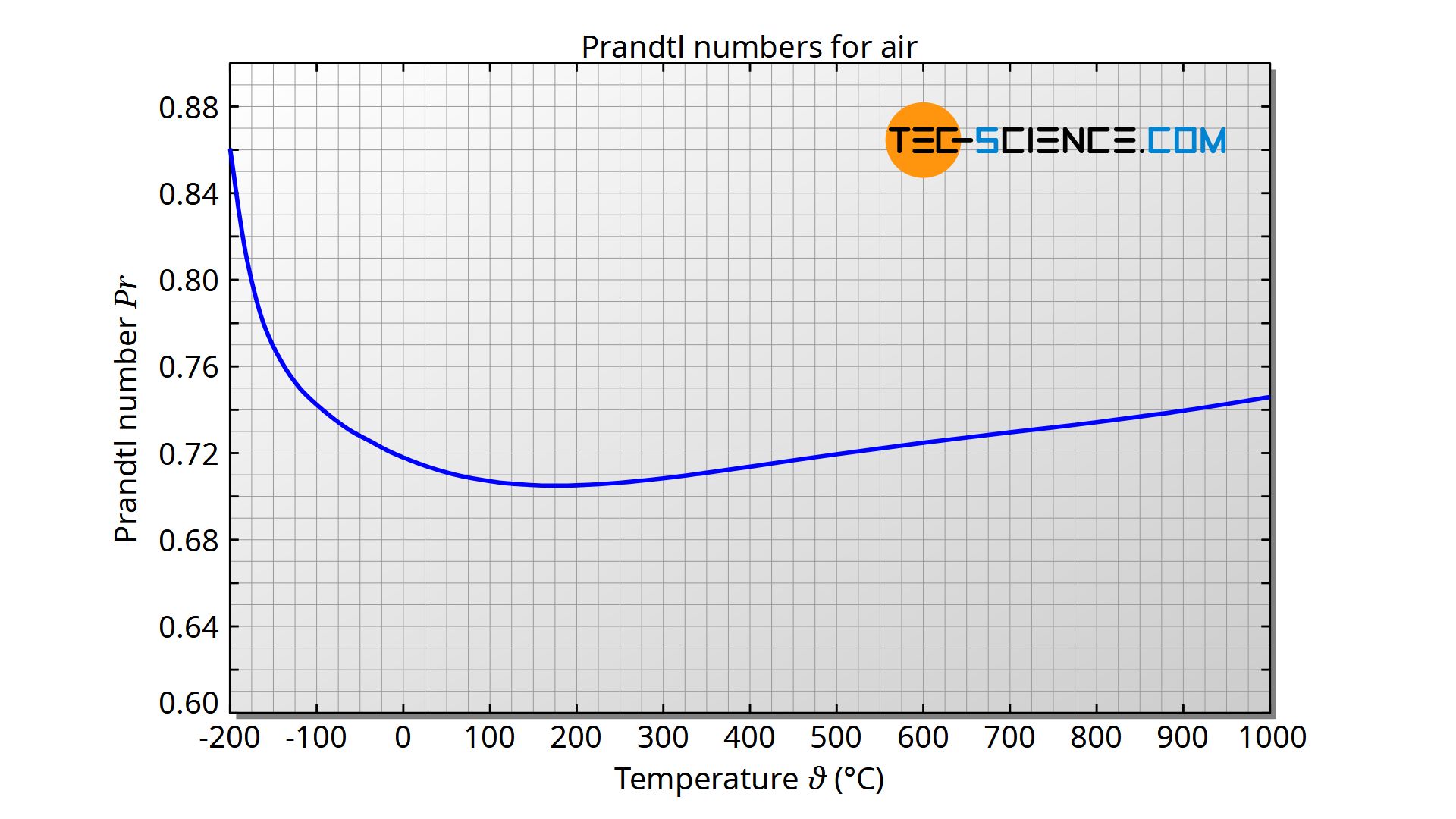
With a Prandtl number of 0.7, air is in a range where the hydrodynamic and thermal boundary layer are approximately equal. As already mentioned, the temperature dependence is relatively low. At an ambient pressure of 1 bar, the Prandtl number only varies by a maximum of 5 % in the range between -100 °C and +500 °C. Using the formula given below, the Prandtl number of air at 1 bar in the temperature range between -100 °C and 500 °C can be calculated with a maximum deviation of 0.1 % from the literature value. The temperature is to be used in the unit “degrees Celsius”.
\begin{align}
&\boxed{Pr_\text{air} = \frac{10^9}{1.1 \cdot \vartheta^3-1200 \cdot \vartheta^2 + 322000 \cdot \vartheta + 1.393 \cdot 10^9}}\\[5px]
&-100 °C <\vartheta < 500 °C \\[5px]
\end{align}
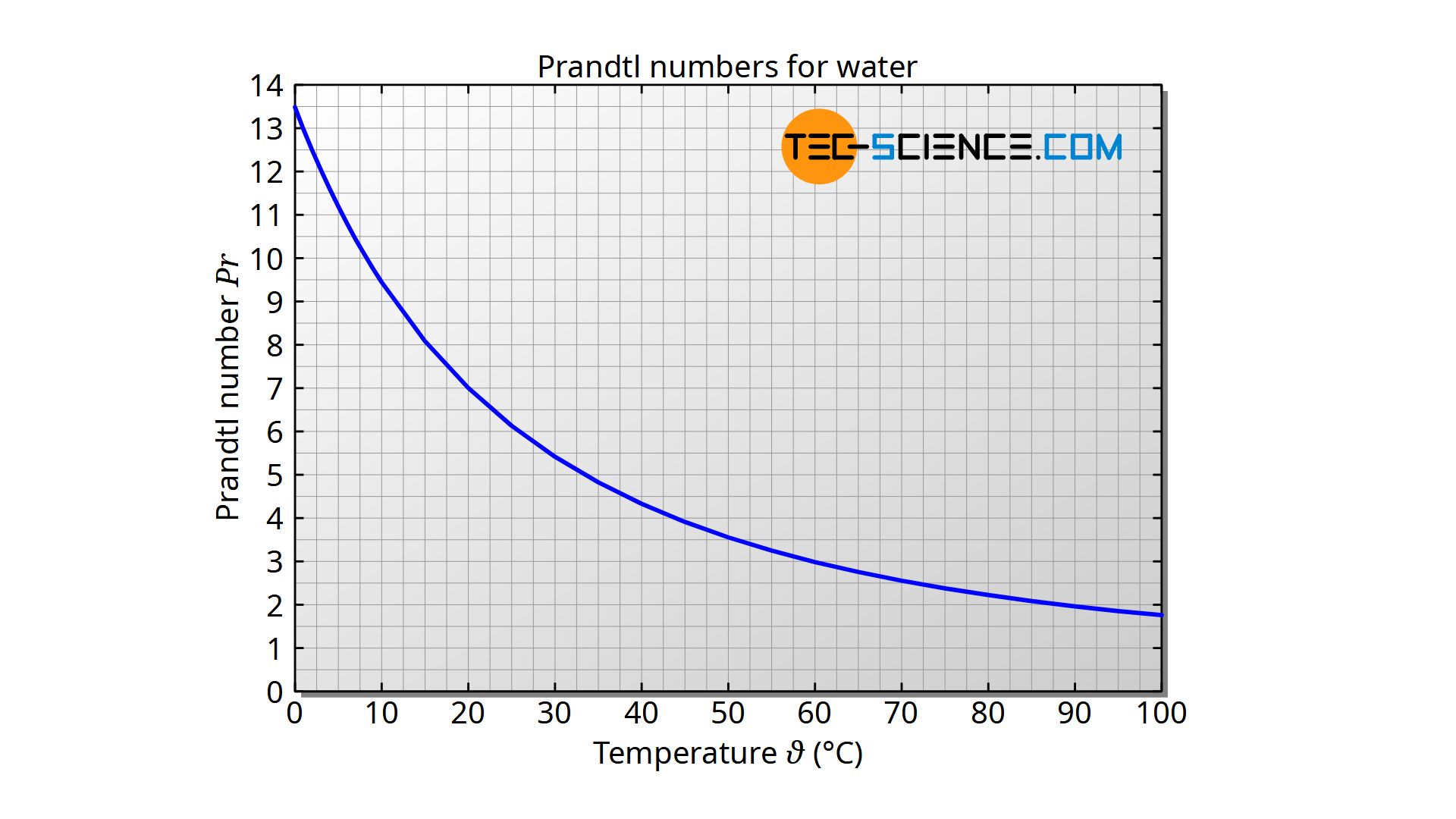
In the case of liquid water, the Prandtl number at a pressure of 1 bar ranges from 13.44 (at 0 °C) to 1.75 (at 100 °C). With the formula given below, the Prandtl number can be determined in the temperature range between 0 and 90 °C with a maximum deviation of 1 % from the literature value. The temperature is to be used in the unit “degrees Celsius”.
\begin{align}
&\boxed{Pr_\text{water} = \frac{50000}{\vartheta^2+155\cdot \vartheta + 3700}} ~~~0 °C <\vartheta < 90 °C\\[5px]
\end{align}