Learn more about calculating the final temperature of a drink when cooling with ice cubes in this article.
Introduction (Excel spreadsheet for calculation)
If you want to cool a warm drink relatively quickly in summer, you usually use ice cubes. The disadvantage, however, is that soft drinks are usually verwässern by the melting of the ice cubes. So wouldn’t it make sense to develop ice cubes that don’t melt? Or couldn’t one simply use copper cubes cooled in the freezer?

In order to answer this question, it will first be shown how the final temperature after complete melting of the ice cubes and mixing with the beverage can be calculated. For simplicity, it is assumed that heat is only transferred between the beverage and the ice cubes. In reality, the surroundings and the glass are also involved in the heat transfer that takes place, but this is neglected in the following.
The entire cooling process can basically be divided into three steps, which will be discussed in more detail below:
- Heating the ice cubes to melting temperature
- Melting of the ice cubes
- Mixing the melted ice with the drink

For all those who do not want to deal with the derivation of the formulas, the final temperature can be calculated directly using the following Excel spreadsheet:
Heating the ice cubes to melting temperature
Ice cubes from the freezer usually have a temperature of about -20 °C. If the ice cubes are added to the beverage, they first heat up to the melting temperature of 0 °C. Using the specific heat capacity of the ice of cice = 2.0 kJ/(kg⋅K) and the mass mice = 50 g, the required heat Qice for this heating process can be determined based on the temperature rise of ΔTice = 20 °C:
\begin{align}
&Q_\text{ice} = c_\text{ice} \cdot m_\text{ice} \cdot \Delta T_\text{ice} \\[5px]
&Q_\text{ice} = 2.0 \tfrac{\text{kJ}}{\text{kg⋅K}} \cdot 0.05 \text{ kg} \cdot 20 \text{ °C} = 2 \text{ kJ}\\[5px]
\end{align}
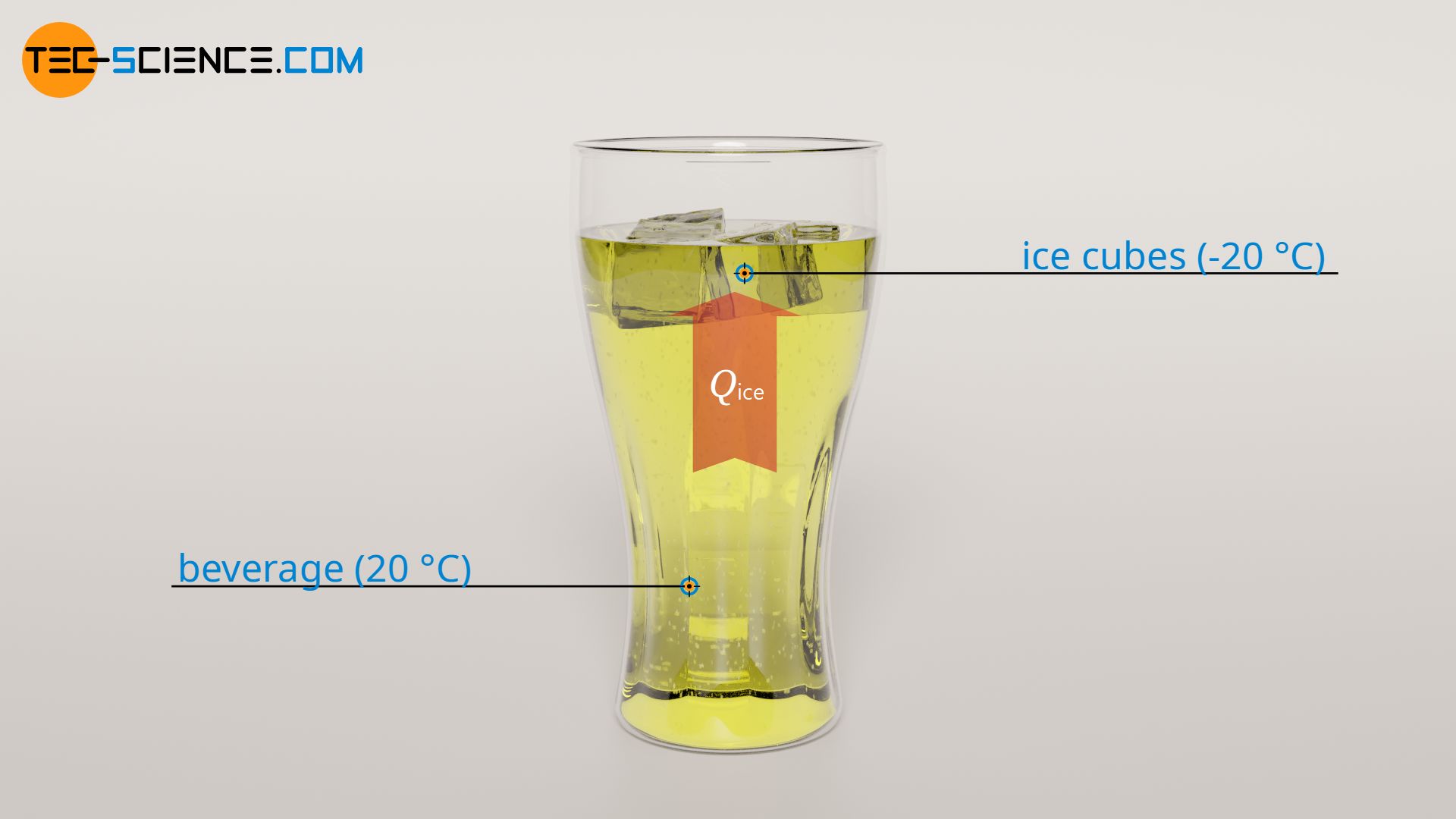
To heat the ice cubes to melting temperature, 2 kJ of heat must be added. This required heat is supplied by the beverage. This means that 2 kJ of heat energy is drawn from the beverage to heat the ice cubes. The temperature of the beverage obviously drops as a result. The amount by which the temperature of the beverage is changed (ΔT1) due to the release of heat Qice can be determined using the specific heat capacity of the beverage cbev and the mass of the beverage mbev. Since most beverages or soft drinks are almost entirely water, the specific heat capacity of water can be used (cbev = 4.2 kJ/(kg⋅K)):
\begin{align}
&Q_\text{ice} = c_\text{bev} \cdot m_\text{bev} \cdot \Delta T_\text{1} \\[5px]
&\Delta T_\text{1} = \frac{Q_\text{ice}}{c_\text{bev} \cdot m_\text{bev}} \\[5px]
&\Delta T_\text{1} = \frac{2 \text{ kJ}}{4.2 \frac{\text{kJ}}{\text{kg⋅K}} \cdot 0.5 \text{ kg}} \approx 1 \text{ °C} \\[5px]
\end{align}
Due to the heating of the ice cubes to melting temperature, the temperature of the beverage decreases by 1 °C. As the temperature of the beverage was 20 °C at the beginning, it now has a temperature of 19 °C.
Melting of the ice cubes
When the ice cubes are heated to melting temperature, they begin to melt. During melting so-called latent heat of fusion Qf is necessary to break the intermolecular bonds. This latent heat of fusion can be determined using the specific latent heat of fusion of ice with qf = 334 kJ/kg and the mass of the ice cubes to be melted of mice = 50 g:
\begin{align}
&Q_\text{f} = q_\text{f} \cdot m_\text{ice} \\[5px]
&Q_\text{f} = 334 \frac{\text{kJ}}{\text{kg}} \cdot 0,05 \text{ kg} = 16.7 \text{ kJ} \\[5px]
\end{align}
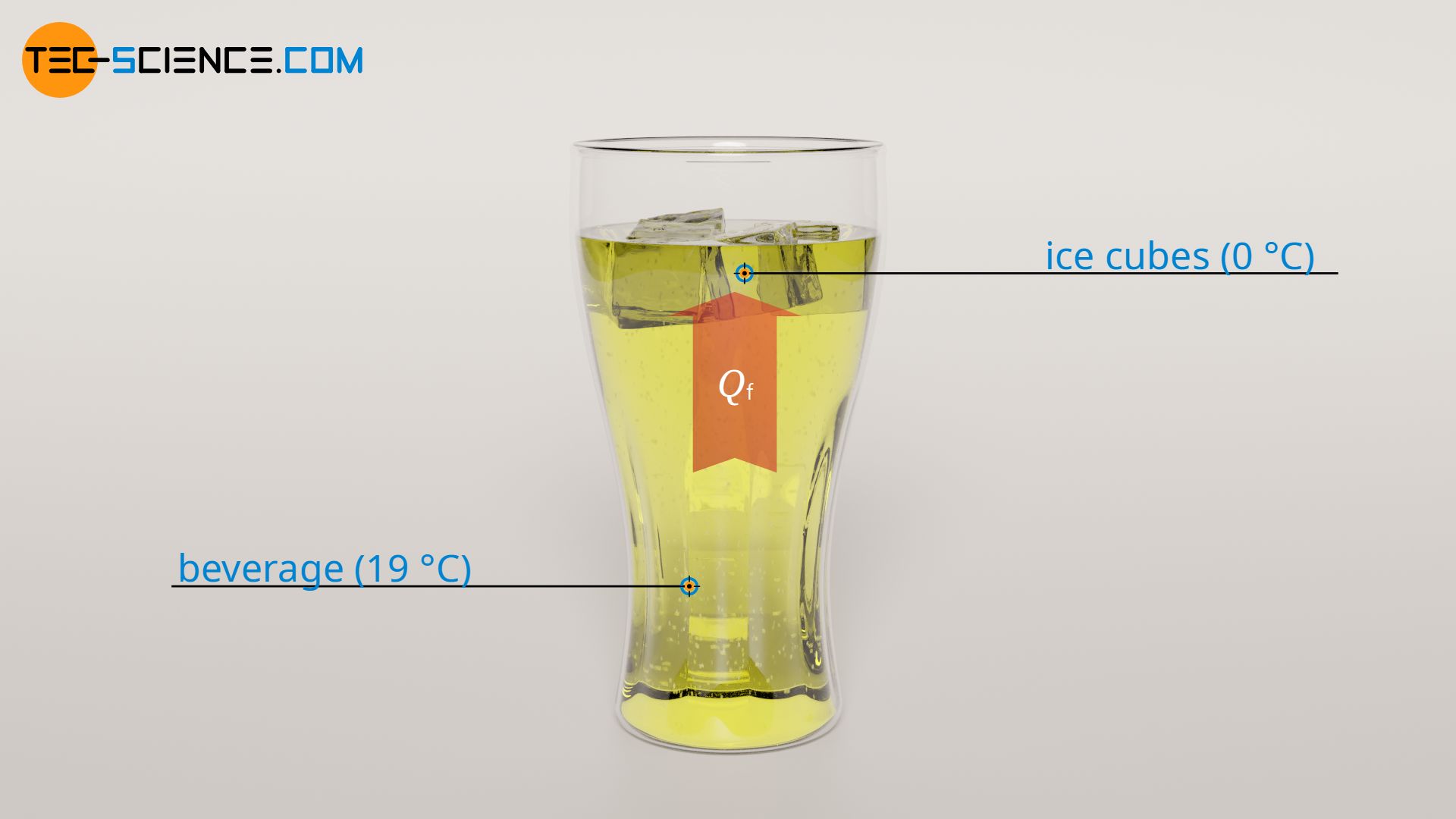
To completely melt the ice cubes, 16.7 kJ of heat energy is required. This amount of heat is also supplied by the beverage. Thus, 16.7 kJ of heat energy is drawn from the beverage during melting. This is significantly more than during the heating of the ice cubes. Accordingly, the associated temperature change of the beverage (ΔT2) is also higher:
\begin{align}
&Q_\text{f} = c_\text{bev} \cdot m_\text{bev} \cdot \Delta T_2 \\[5px]
&\Delta T_2 = \frac{Q_\text{f}}{c_\text{bev} \cdot m_\text{bev}} \\[5px]
&\Delta T_2 = \frac{16.7 \text{ kJ}}{4.2 \frac{\text{kJ}}{\text{kg⋅K}} \cdot 0.5 \text{ kg}} \approx 8 \text{ °C} \\[5px]
\end{align}
Due to the melting of the ice cubes, the temperature of the beverage decreases by 8 °C. Since the temperature of the beverage before melting was 19 °C, it now has a temperature of 11 °C.
Mixing the melted ice with the beverage (final temperature)
Although mixing of the 0 °C cold melted water with the beverage takes place at the same time as the ice cubes melt, this process can be considered separately from an energy point of view. This means that first the ice cubes are completely melted, as considered in the previous section. Afterwards the mixing between 0 °C cold melted water (Tw) and 11 °C cold beverage (Tbev) is considered. The final temperature of the mixture can be calculated with the Richmann’s law of mixtures:
\begin{align}
\boxed{T_\text{f} = \frac{c_\text{bev} \cdot m_\text{bev} \cdot T_\text{bev} + c_\text{w} \cdot m_\text{w} \cdot T_\text{w}}{c_\text{bev} \cdot m_\text{bev} + c_\text{w} \cdot m_\text{w}}} ~~~\text{Richmann’s law} \\[5px]
\end{align}

For the specific heat capacity of the melted ice cubes cw, as for the beverage, the specific heat capacity of water with cw= 4.2 kJ/(kg⋅K) is used (in this case the specific heat capacities cancel each other out in the above formula). The mass of the melted water mw is equal to the mass of the ice cubes with mw = 50 g. The final mixing temperature Tf can thus be determined as follows:
\begin{align}
\require{cancel}
&T_\text{f} = \frac{\cancel{c_\text{bev}} \cdot m_\text{bev} \cdot T_\text{bev} + \cancel{c_\text{w}} \cdot m_\text{w} \cdot T_\text{w}}{\cancel{c_\text{bev}} \cdot m_\text{bev} + \cancel{c_\text{w}} \cdot m_\text{w}} \\[5px]
&T_\text{f} = \frac{ m_\text{bev} \cdot T_\text{bev} + m_\text{w} \cdot T_\text{w}}{m_\text{bev} + m_\text{w}} \\[5px]
&T_\text{f} = \frac{ 0.5 \text{ kg} \cdot 11 \text{ °C} + 0.05 \text{ kg} \cdot 0 \text{ °C}}{0.5 \text{ kg} + 0.05 \text{ kg}} = 10 \text { °C} \\[5px]
\end{align}
The mixing thus causes the temperature of the beverage to drop again by ΔT3 = 1 °C to a total of 10 °C.
Conclusion
If we look at the cooling of the beverage, which was divided into three steps, the following temperature change of the beverage can be seen in the respective cases:
- Temperature change due to the heating the ice cubes: ΔT1 = 1 °C
- Temperature change due to the melting of the ice cubes: ΔT2 = 8 °C
- Temperature change due to mixing of the melted water: ΔT3 = 1 °C
Obviously, the largest temperature change is due to the melting of the ice cubes. This is because of the relatively large heat of fusion of water compared to the small amounts of heat transferred during the heating of the ice cubes or mixing. It is therefore essential for the cooling effect that the ice cubes melt! In this respect, a compromise must always be made between the desired cooling and the watering down of the beverage by the melted ice cubes.

If one were to use the aforementioned copper cubes instead of ice cubes, which one cools to -20 °C in the freezer, one would only obtain a final temperature of the beverage of 16.7 °C. Copper obviously does not melt when added to a beverage. It is only a “mixing” that can be described by Richmann’s law of mixtures. The copper cubes have a specific heat capacity of 0.385 kJ/(kg⋅K) and a mass of 0.488 kg (with identical volume to the 50-gram ice cubes):
\begin{align}
\require{cancel}
&T_\text{f} = \frac{c_\text{bev} \cdot m_\text{bev} \cdot T_\text{bev} + c_\text{co} \cdot m_\text{co} \cdot T_\text{co}}{c_\text{bev} \cdot m_\text{bev} + c_\text{co} \cdot m_\text{co}} \\[5px]
&T_\text{f} = \frac{ 0.5 \text{ kg} \cdot 4.2 \frac{\text{kJ}}{\text{kg⋅K}} \cdot 20 \text{ °C} + 0.488 \text{ kg} \cdot 0.385 \frac{\text{kJ}}{\text{kg⋅K}} \cdot (-20 \text{ °C})}{0.5 \text{ kg} \cdot 4.2 \frac{\text{kJ}}{\text{kg⋅K}} + 0.488 \text{ kg} \cdot 0.385 \frac{\text{kJ}}{\text{kg⋅K}}} \\[5px]
&T_\text{f} = 16.7 \text{ °C} \\[5px]
\end{align}






