In this article you will find formulas for calculating the local and average Nusselt numbers for forced flows over plates and in pipes with circular cross sections.
Nusselt number
The definition and importance of the Nusselt number as a similarity parameter has already been explained in detail in the linked article. With this parameter, the heat transfer coefficient can be calculated as a function of the characteristic length of the system. Thus, the heat flux can be determined on the basis of the temperature difference between wall and fluid. The heat flux represents the heat flow per unit area that is transferred from the wall to the flowing fluid (for heated walls) or from the flowing fluid to the wall (for heated fluids).
\begin{align}
\label{qq}
&\boxed{\dot q = \alpha \cdot \Delta T} \\[5px]
&\boxed{\alpha = Nu \cdot \frac{\lambda_f}{L}} \\[5px]
\end{align}
\begin{align}
\notag&\dot q ~&& \text{heat flux} \\[5px]
\notag&\alpha ~&& \text{heat transfer coefficient} \\[5px]
\notag&\Delta T~&& \text{temperature difference between wall and fluid} \\[5px]
\notag&Nu~&& \text{Nusselt number} \\[5px]
\notag&\lambda_f~&& \text{thermal conductivity of the fluid} \\[5px]
\notag&L~&& \text{characteristic length of the system} \\[5px]
\end{align}
The characteristic length corresponds to the inner diameter of the pipe in the case of a pipe flow or to the length of a plate in the direction of flow in the case of a plate which is flowed around by a fluid. In the cases where a fluid flows around an object, the fluid temperature for calculating the temperature difference refers to the temperature in the freestram (Tf,∞). For fluids in pipes, the adiabatic mixing temperature (Tf) is taken as the basis to calculate local heat transfer, i.e. the temperature that would be obtained if the fluid were ideally mixed at the point of interest.
Dependence of the Nusselt number
In principle, the Nusselt number is not a material constant, but is determined to a large extent by the properties of the flow with regard to velocity and thermal conduction. The flow velocity is characterized by the dimensionless Reynolds number Re. The the thermal conductivity is also taken into account with a dimensionless parameter, the so-called Prandtl number Pr. The Prandtl number describes the transport of momentum between the flowing fluid layers in relation to the transport of heat by thermal conduction. Thus, the following functional dependence applies to the Nusselt number in general:
\begin{align}
&\overline{Nu}= \overline{Nu} (Re, Pr) \\[5px]
\end{align}
Note that when using the Reynolds number, the type of flow plays a decisive role, i.e. whether the flow is laminar or turbulent. In turbulent flows, the Nusselt numbers generally assume very large values, since the mixing caused by the turbulences leads to an increased transport of momentum and energy transverse to the flow direction. This results in a large heat flow.
In the following, the calculation of the Nusselt numbers will be shown for the following cases:
- flow around a flat plate
- flow through a pipe with circular cross-section
The calculations are essentially based on the VDI Wärmeatlas (7th edition, 1994). The formulas apply exclusively to forced flows by pumps or fans and not to free convection.
Calculation of the Nusselt number for flat plates
Laminar flow
For Reynolds numbers smaller than 10,000 and Prandtl numbers between 0.6 and 2000, the average Nusselt number for a laminar flow around a flat plate which is isothermally heated or cooled can be calculated using the following formula:
\begin{align}
\label{nul}
&\boxed{\overline{Nu}_\text{lam}= 0.664 \cdot \sqrt{Re} \cdot \sqrt[3]{Pr}} \\[5px]
& Re<10^5 ~~\text{and}~~0.6<Pr<2000 \\[5px]
\end{align}

The material values for calculating the Reynolds and Prandtl numbers refer to the mean temperature of the flowing fluid. If T1 denotes the temperature of the fluid at the beginning of the plate and T2 the temperature at the end, then the mean temperature is calculated with the following formula:
\begin{align}
\label{mean}
T_m = \frac{T_1+T_2}{2}
\end{align}
In order to ensure a laminar flow around the plate, the edge should be as streamlined as possible. Otherwise a sharp edge will cause vortices and thus turbulences in the boundary layer.
Turbulent flow
If the flow around the isothermally heated or cooled plate is a turbulent flow, the following formula can be used to calculate the average Nusselt number at constant wall temperature. This formula is based on the studies of Petukov (High Temperature I, 1963) and Schlichting (Grenzschicht-Theorie, 1958).
\begin{align}
\label{nut}
&\boxed{\overline{Nu}_\text{tur}= \frac{0.037 \cdot Re^{0.8}\cdot Pr}{1+2.443 \cdot Re^{-0,1} \left(Pr^{\frac{2}{3}}-1\right)} } \\[5px]
&5 \cdot 10^5 <Re<10^7 ~~\text{and}~~0.6<Pr<2000\\[5px]
\end{align}

The Reynolds numbers are, by definition, above the critical Reynolds numbers in turbulent flows. For the validity of the above formula, the Reynolds numbers should therefore lie in the range between 5⋅105 and 107. The Prandtl numbers should be in the range between 0.6 and 2000 for the formula to be valid. The material values for determining these dimensionless parameters refer to the mean temperature of the fluid [see formula (\ref{mean})].
Laminar and turbulent flow
In practice, even with moderate Reynolds numbers the flow is not completely laminar in many cases. The reason for this is the mostly non-streamlined edge of the plate. Furthermore, in practice the plate is never flowed against exactly parallel, i.e. the flow already contains a low degree of turbulence. After a region where the flow is almost laminar, the flow therefore changes into a turbulent flow. A laminar sublayer is developed along the entire plate.

For the critical Reynolds number Recrit, from which a transition from laminar to turbulent flow is to be expected, applies:
\begin{align}
&\boxed{Re_\text{crit}= \frac{v_\infty \cdot x_\text{crit}}{\nu}=5 \cdot 10^5} \\[5px]
\end{align}
In this formula, v∞ denotes the flow velocity of the freestream.
For flows with laminar-turbulent transition with Reynolds numbers between 10 und 107 the average Nusselt number ist calculated with the following formula:
\begin{align}
\label{nuu}
&\boxed{\overline{Nu}= \sqrt{\overline{Nu}_\text{lam}^2 + \overline{Nu}_\text{tur}^2}} \\[5px]
&10 < Re < 10^7 ~~\text{and}~~0.6<Pr<2000\\[5px]
\end{align}
The Nusselt numbers Nulam and Nutur are to be calculated with the formulas (\ref{nul}) and (\ref{nut}).
Taking into account the direction of the heat flow and the temperature dependence of the material properties
When calculating the Nusselt numbers, it must always be taken into account whether heat is transferred from the fluid to the plate or vice versa. Depending on the case, there is a different temperature distribution in the fluid despite identical fluid temperatures (which is related to the temperature of the freestream). This has an effect on the material properties of the fluid.
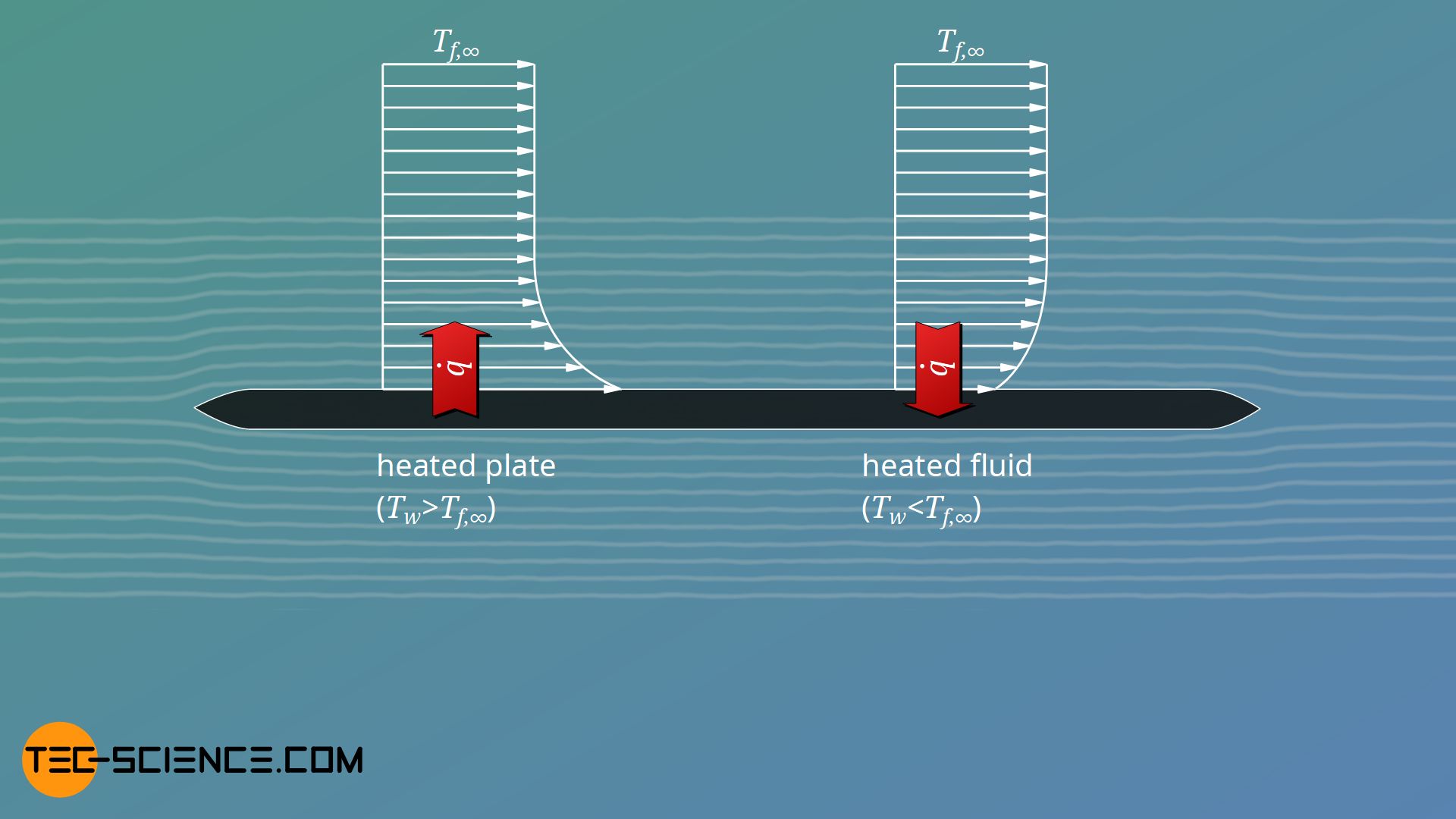
For example, the viscosity of liquids decreases with increasing temperature. This influences the velocity boundary layer and thus the heat transfer. For liquids, these dependencies can be taken into account by the factor given below, which is to be applied to the calculated Nusselt numbers:
\begin{align}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{Pr}{Pr_w}\right)^{0.25} } ~~~~~\text{for liquids}\\[5px]
\end{align}
Not only the direction of the heat flow, but also the general dependence of the material values on the temperature is taken into account in this way. The Prandtl number Pr refers to the mean liquid temperature, whereas the Prandtl number Prw refers to the material values of the liquid at wall temperature. For gases, the factor for taking into account the temperature dependence is usually based directly via the ratio of the temperatures between fluid and wall, since for gases the Prandtl number is not strongly influenced by the temperature:
\begin{align}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{T_f}{T_w}\right)^{0.12} } ~~~~~\text{for gases}\\[5px]
\end{align}
Calculation of the Nusselt number for forced pipe flows
Definition of the average heat transfer coefficient
In the following we consider the flow of a fluid through a heated or cooled pipe with the constant wall temperature Tw. The temperature of the fluid at the beginning of the pipe is denoted by T1 and at the end of the pipe by T2. However, the fluid at the end of the pipe does not have a uniform temperature profile. The temperature T2 therefore refers to the adiabatic mixing temperature.
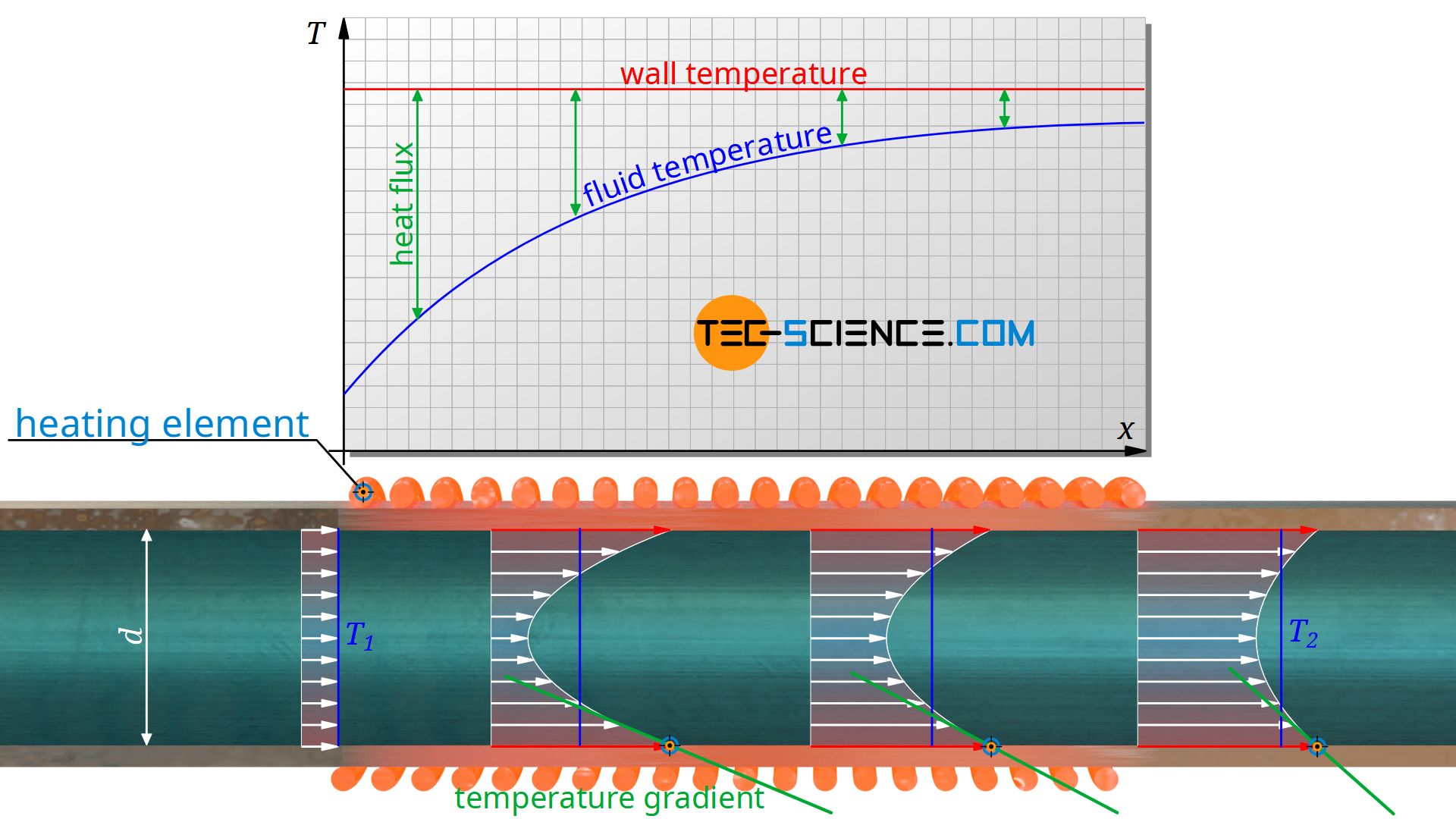
To calculate the convective heat transfer according to equation (\ref{qq}) the temperature difference between wall and fluid is decisive. However, the fluid temperature changes over the length of the pipe. For an isothermally heated pipe, the temperature of the fluid increases permanently as it flows through it. At the beginning, more heat is transferred due to the relatively large temperature difference between wall and fluid than towards the end of the pipe. The temperature difference is therefore defined as a logarithmic temperature difference ΔTln:
\begin{align}
&\boxed{\Delta T_\text{ln}:=\frac{\Delta T_\text{in}-\Delta T_\text{out}}{\ln\left(\frac{\Delta T_\text{in}}{\Delta T_\text{out}} \right)}} ~~~~~\text{logarithmic temperature difference} \\[5px]
&\Delta T_\text{ln}=\frac{(T_\text{w}-T_1)-(T_\text{w}-T_2)}{\ln\left(\frac{T_\text{w}-T_1}{T_\text{w}-T_2} \right)} \\[5px]
\end{align}
With α as the mean heat transfer coefficient, the average heat flux of the pipe can be calculated with the following formula:
\begin{align}
&\boxed{\overline{\dot q} = \overline{\alpha} \cdot \Delta T_\text{ln} } \\[5px]
\end{align}
The average heat transfer coefficient is determined by the average Nusselt number (the inner diameter d of the pipe corresponds to the characteristic length):
\begin{align}
&\boxed{\overline{\alpha} =\overline{Nu} \cdot \frac{\lambda_f}{d}} \\[5px]
\end{align}
Definition of the profile factors
For pipe flows, the temperature profile and thus the Nusselt number does not only depend on the Reynolds number and the Prandtl number. It must also be taken into account which inner diameter d the pipe has in relation to its length l. The average Nusselt number Nu therefore generally depends on the following average profile factor β:
\begin{align}
&\boxed{\overline{\beta}:=Re \cdot Pr \cdot \frac{d}{l}} ~~~~~\text{average profile factor} \\[5px]
&\boxed{\overline{Nu}=\overline{Nu}(\overline{\beta})} \\[5px]
\end{align}
The length l does not necessarily refer to the entire pipe, but basically only to that section within which a heat transfer between pipe and fluid takes place. For the sake of simplicity, however, l is usually called pipe length.
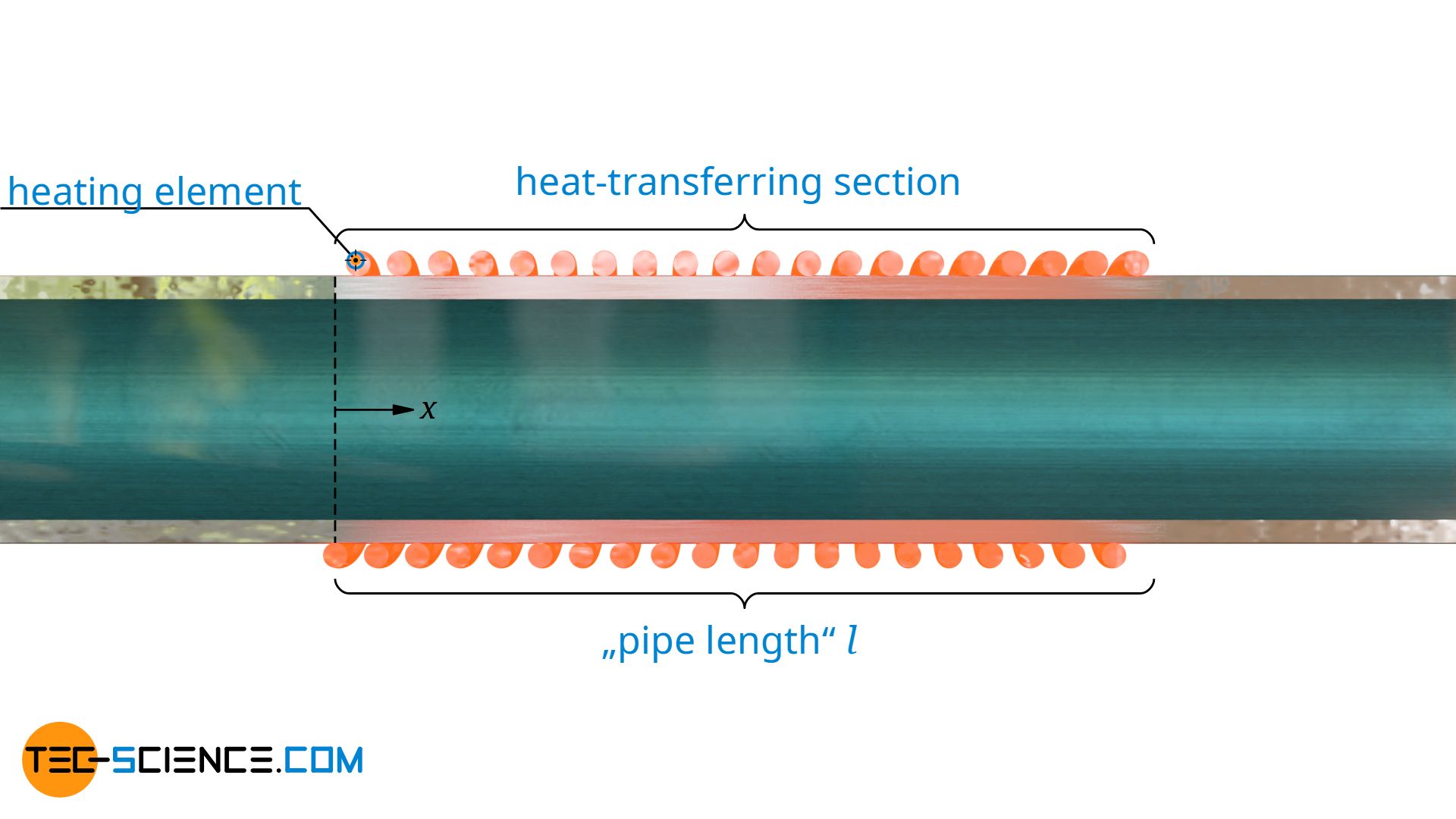
For calculating the local Nusselt number Nu, only the distance x up to the point of interest is to be used as the characteristic length. Thus, the local profile factor β is calculated with the formula given below.
\begin{align}
&\boxed{\beta:=Re \cdot Pr \cdot \frac{d}{x}} ~~~~~\text{local profile factor} \\[5px]
&\boxed{Nu=Nu(\beta)} \\[5px]
\end{align}
The material values for the calculation of the Reynolds and Prandtl numbers again refer to the mean temperature of the fluid. If T1 denotes the temperature of the fluid at the beginning of the heat transfer and T2 the temperature of the fluid at the end of the heat transfer (mixing temperature), then the mean temperature is calculated with the following formula:
\begin{align}
T_m = \frac{T_1+T_2}{2}
\end{align}
The product of Reynolds number and Prandtl number is also called Péclet-number Pe. The profile factor can therefore also be defined by the Péclet-number:
\begin{align}
&\boxed{Pe:=Re \cdot Pr}= \frac{v \cdot L}{a} &&~~~~~\text{Péclet number} \\[5px]
&\beta=Pe \cdot \frac{d}{l} &&~~~~~\text{average profile factor} \\[5px]
&\beta=Pe \cdot \frac{d}{x} &&~~~~~\text{local profile factor} \\[5px]
\end{align}
Note that the Péclet-number is only determined by the mean flow velocity v, the thermal diffusivity “a” of the fluid and the characteristic length L of the system. It is not dependent on the viscosity of the fluid! In this respect, the viscosity of the fluid is not important for the heat transfer in pipes explained below.
Limit values of the Nusselt numbers
In the article on the Nusselt number, it was shown that, depending on the boundary condition and under the prerequisite of a hydrodynamically and thermally fully developed pipe flow, the Nusselt numbers approach the following asymptotes:
\begin{align}
\label{366}
&\boxed{Nu_{\infty}= 3.660} &&~~~\text{for constant wall temperature}\\[5px]
\label{4364}
&\boxed{Nu_{\infty}= 4.364} &&~~~\text{for constant heat flux at the wall}\\[5px]
\end{align}
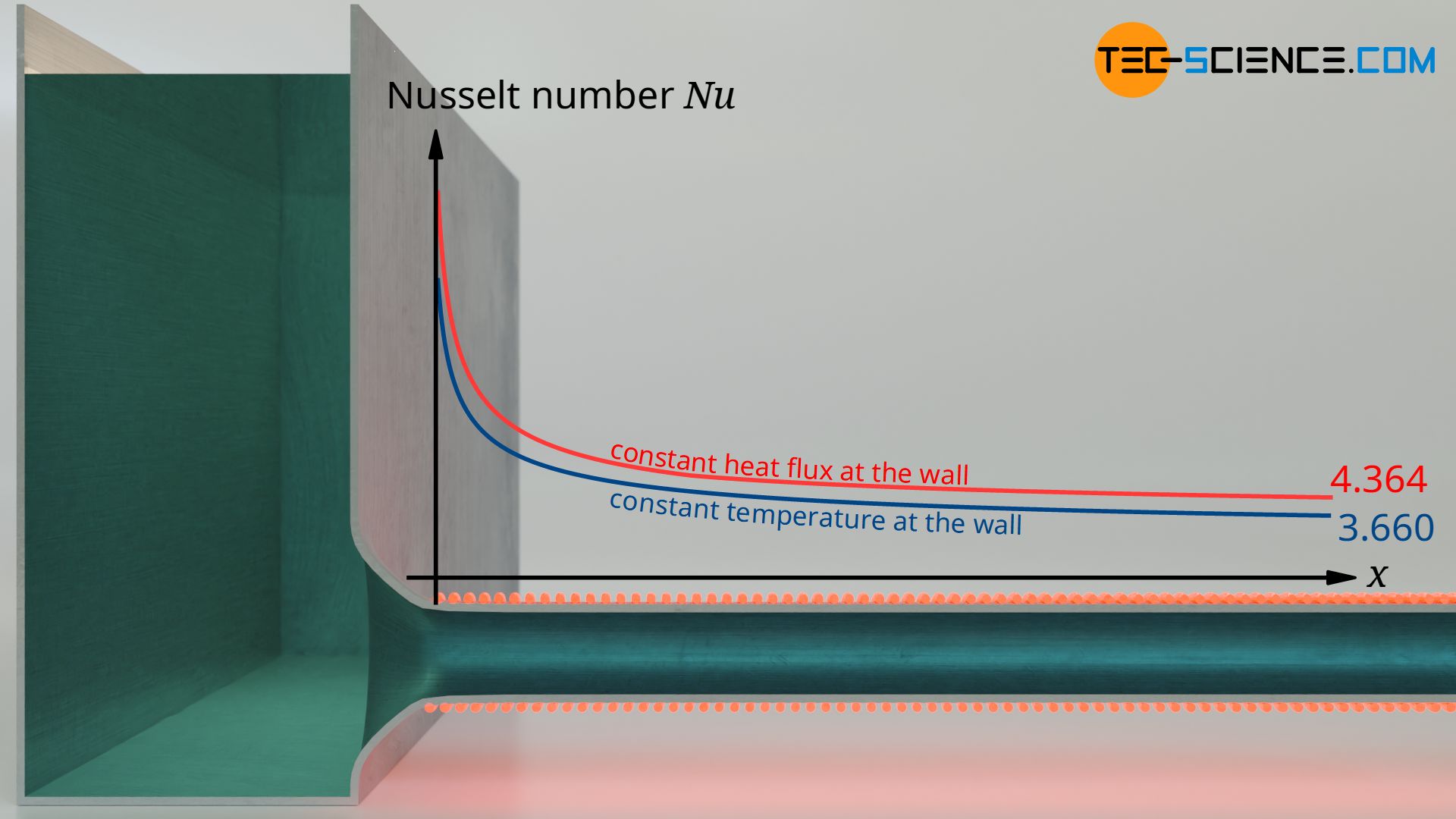
This is remarkable in that neither the Reynolds number nor the Prandtl number influences these asymptotes. However, these limit values only apply to fully developed flows, which in practice are generally not given for finite pipe lengths.
Laminar flow at constant wall temperature
Fully developed hydrodynamic flow (long pipes)
The average Nusselt number Nu for a hydrodynamically fully developed flow (fully developed velocity profile) can be calculated with the following formula using the average profile factor β:
\begin{align}
\label{nu_lg}
&\boxed{\overline{Nu}= \sqrt[3]{49.371 + \left(1.615 \cdot \sqrt[3]{\overline{\beta}}-0.7 \right)^3} } \\[5px]
&\overline{\beta}=Re \cdot Pr \cdot \frac{d}{l}\\[5px]
\end{align}
A fully developed flow is present, for example, if the fluid has already flowed through a sufficiently long pipe section before it reaches the actual heat-transferring pipe section of length l.
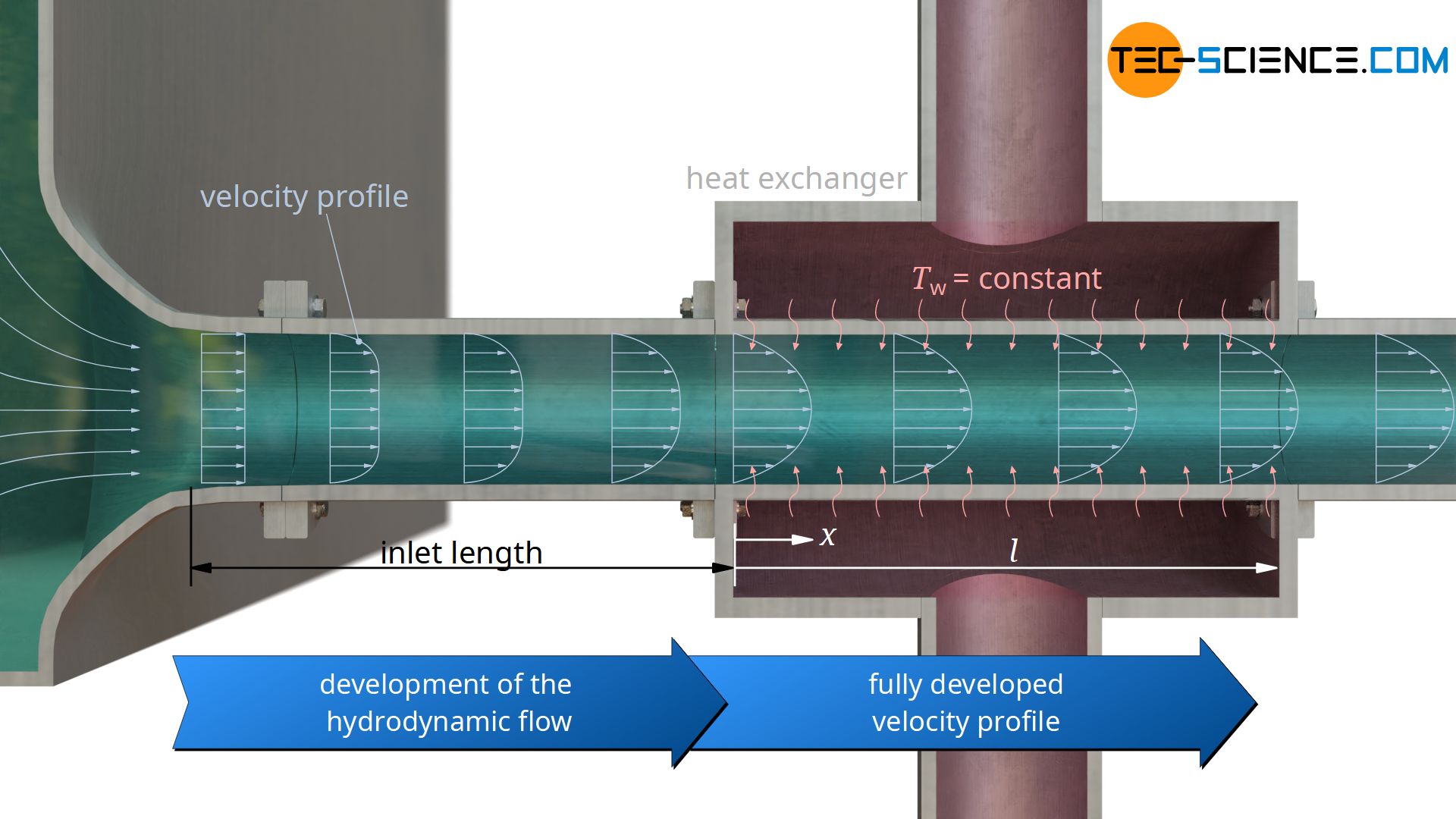
The local Nusselt number Nu at a certain position x, measured from the beginning of the heat transfer, can be determined by means of the local profile factor β:
\begin{align}
\label{nu_ll}
&\boxed{Nu= \sqrt[3]{49.371 + \left(1.077 \cdot \sqrt[3]{\beta}-0.7 \right)^3} } \\[5px]
&\beta=Re \cdot Pr \cdot \frac{d}{x} \\[5px]
\end{align}
Note that the profile factors in the formulas above are close to zero for very long pipes. In these cases, the Nusselt number approaches more and more the asymptote of 3.660 [see equation (\ref{366})]:
\begin{align}
& \lim \limits_{l \to \infty}\beta \rightarrow 0 ~~~\Rightarrow~~~ Nu\rightarrow 3.660 \\[5px]
\end{align}
Taking into account the development of the flow (short pipes)
In the following we consider a fluid that flows through a pipe and is heated or cooled from the beginning of the pipe. For this purpose, we can imagine a large tank from which liquid flows out through an attached pipe that is heated. In this case, the hydrodynamic flow profile (velocity profile) will only be fully developed after a certain distance (inlet flow).
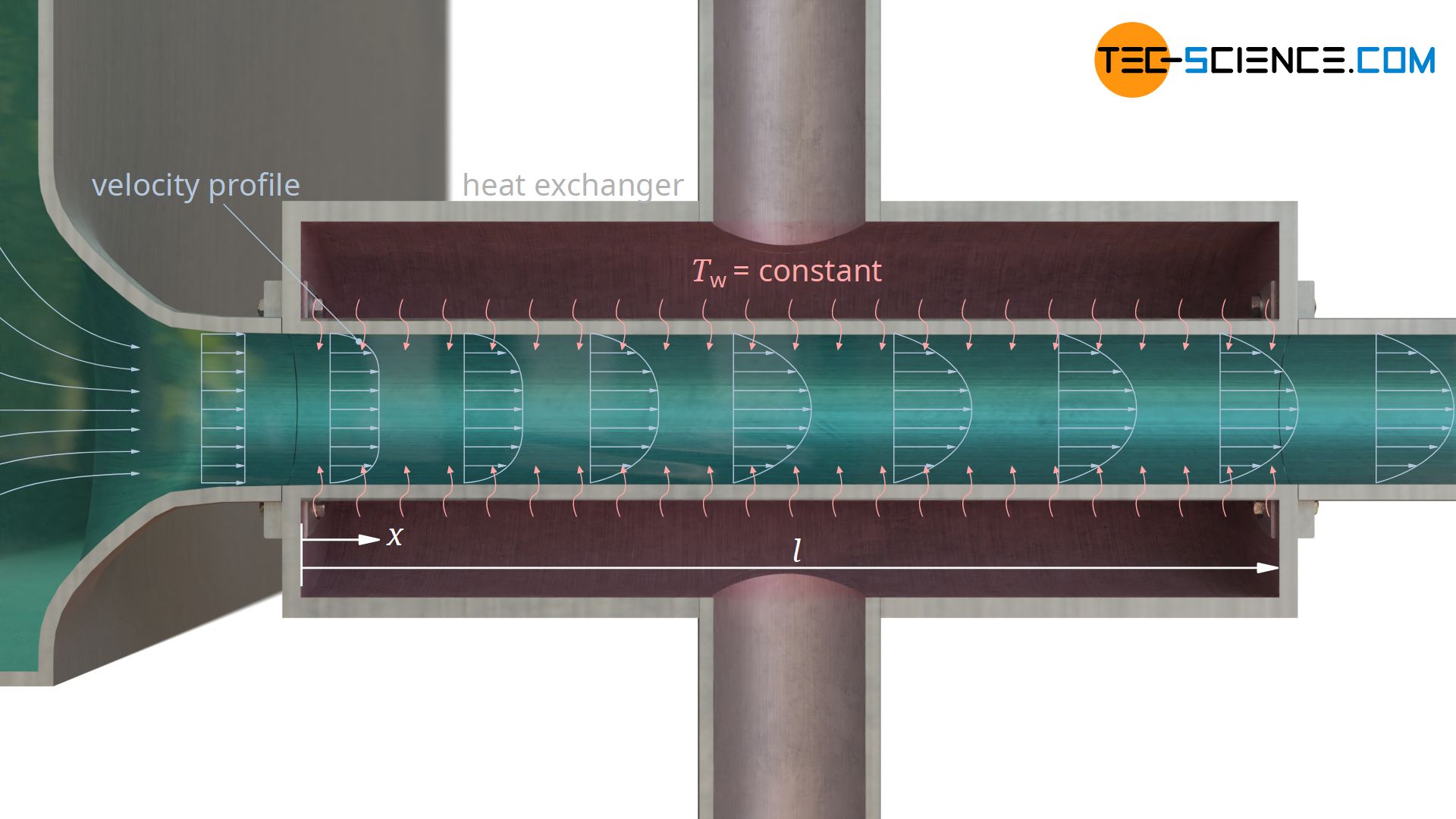
The reason for this is due to the viscosity of the fluid and the associated fluid friction. This leads to a deceleration of the fluid at the wall and to an acceleration in the middle of the pipe due to the conservation of mass. For a Newtonian fluid with constant viscosity, a parabolic velocity profile would develop over the inlet length (Poiseuille flow). In this case, however, this can no longer be assumed, since the fluid does not have a constant temperature across the cross-section when heated or cooled. Thus, the viscosity is also no longer constant.
Regardless of the exact velocity profile, it is a fact that a different profile is present within the inlet length than when the flow is fully developed. However, the velocity profile influences the temperature profile and thus also the entire heat transfer. For this reason, different Nusselt numbers apply when taking into account the development of the flow than with an already developed flow.
This is particularly important for short pipes, where the inlet length has a relatively large proportion of the total pipe length. It can be assumed that due to the higher flow velocity at the wall, much more heat is transported away from the wall than in a fully developed flow, where the flow velocity at the wall has dropped to zero (non-slip condition). The temperature gradient at the wall is thus greater with a non-developed flow, which results in a higher heat transfer and thus higher Nusselt numbers.
If a flow is not fully developed, larger Nusselt numbers can be assumed than if the a flow is fully developed!
For fluids with small Prandtl numbers, which by definition have a relatively high thermal diffusivity compared to their viscosity (e.g. liquid metals such as mercury), the influence of the development of the flow on the Nusselt number is less pronounced. This is because with such fluids, the heat is transferred away from the wall very quickly anyway due to the high thermal conductivity; the influence of the velocity profile does not play the decisive role here.
Conversely, this means that for fluids with relatively large Prandtl numbers, the influence of the development of the flow is relatively strong. In order to take this fact into account, the equations (\ref{nu_lg}) and (\ref{nu_ll}) are therefore modified by the terms marked in red, which are explicitly dependent on the Prandtl number.
The local Nusselt number can be calculated with the formula given below, taking into account the development of the flow:
\begin{align}
&\boxed{Nu= \sqrt[3]{49.371 + \left(1.077 \cdot \sqrt[3]{\beta}-0.7 \right)^3 + \color{red}{\sqrt{\frac{0.03125}{1+22 \cdot Pr}\cdot \beta^3}} } } \\[5px]
&\text{mit}~~~\beta=Re \cdot Pr \cdot \frac{d}{x}\\[5px]
\end{align}
The following formula is used to calculate the average Nusselt number:
\begin{align}
&\boxed{\overline{Nu}= \sqrt[3]{49.371 + \left(1.615 \cdot \sqrt[3]{\beta}-0.7 \right)^3 + \color{red}{\sqrt{\frac{2}{1+22 \cdot Pr}\cdot \beta^3}} } } \\[5px]
&\text{mit}~~~\beta=Re \cdot Pr \cdot \frac{d}{l}\\[5px]
\end{align}
Because in the equations above the profile factor in the term marked in red influences the Nusselt number with the third power, this term is close to zero very fast for large values of x or l. Thus, the Nusselt numbers come closer and closer to the Nusselt numbers for a fully developed flow according to equation (\ref{nu_ll}) or (\ref{nu_lg}).
Taking into account the direction of the heat flow and the temperature dependence of the material properties
Since the Prandtl numbers for liquids are relatively strongly dependent on temperature, it again makes a difference whether the fluid transfers heat to the pipe or whether the pipe transfers heat to the fluid. Depending on this, different temperature profiles are obtained in the fluid, which have an effect on the Prandl numbers.
Hufschmidt and Burck (International Journal of Heat and Mass Transfer, 1968) therefore introduce a correction factor that takes into account the direction of the heat flow and the temperature dependence of the material values. This factor is to be applied to the calculated average Nusselt numbers:
\begin{align}
\label{temp}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{Pr}{Pr_w}\right)^{0.11} } ~ \text{valid for liquid}\\[5px]
\end{align}
The Prandtl number Pr refers to the mean liquid temperature, while the Prandtl number Prw refers to the material values at wall temperature.
Due to the relatively small effects in the case of flowing gases, there is usually no correction factor. According to the VDI Wärmeatlas (7th edition, 1994) the influence of the temperature on the Nusselt number for air, nitrogen and helium as less than 10 % as long as the gas and wall temperatures do not differ from each other by more than a factor of 2 (for the unit Kelvin!).
Laminar flow with constant heat flux at the wall
Fully developed hydrodynamic flow (long pipes)
In the following, we consider a fully developed flow through a pipe with a constant heat flux at the wall. This is the case with electrically heated pipes, for example. The local Nusselt number at a location x, measured from the start of heating or cooling, can be calculated with the following formula:
\begin{align}
\label{96}
&\boxed{Nu= \sqrt[3]{84.11 + \left(1.302 \cdot \sqrt[3]{\beta}-1 \right)^3} } \\[5px]
& \beta=Re \cdot Pr \cdot \frac{d}{x}\\[5px]
\end{align}
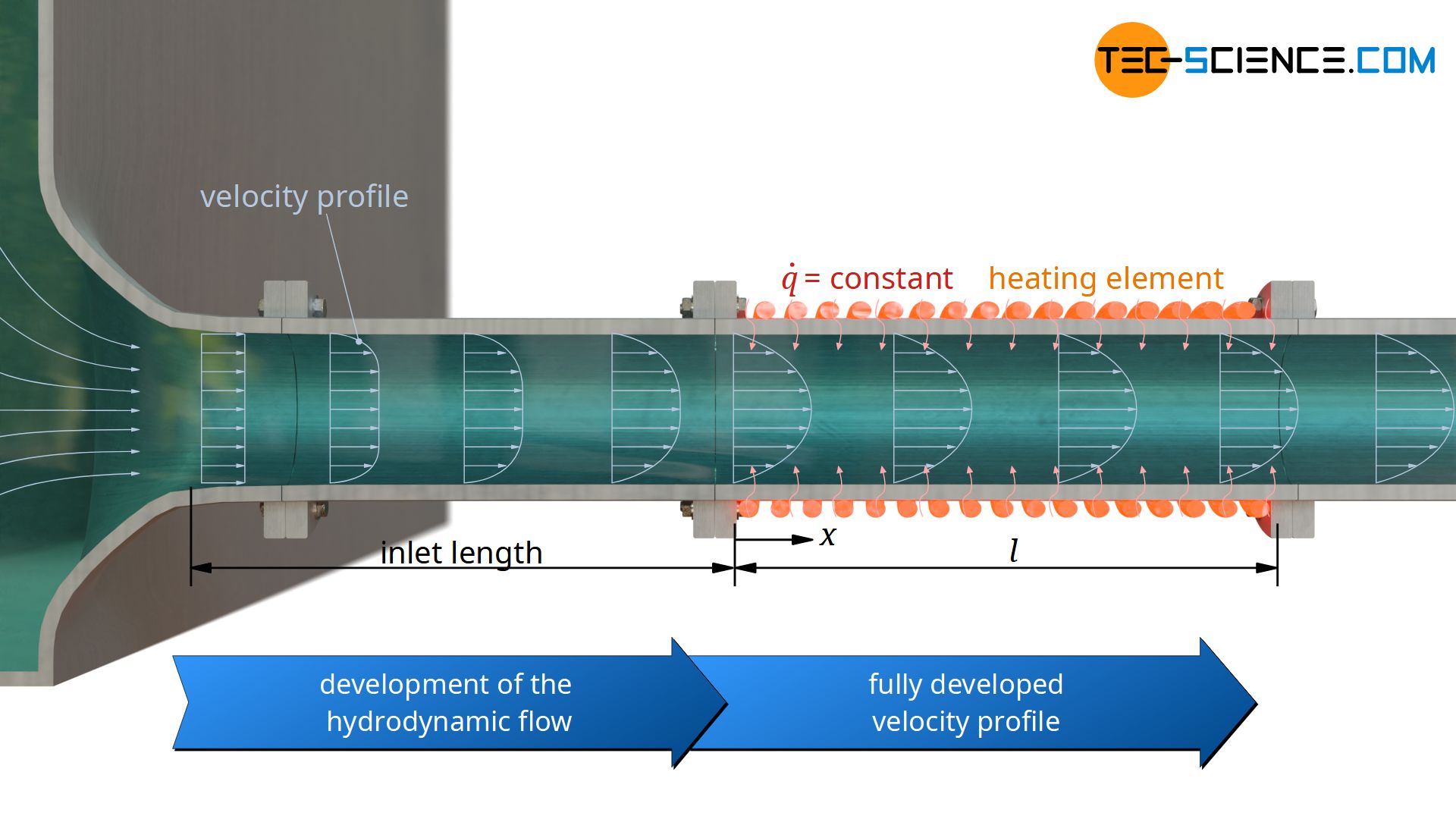
The integration of the local Nusselt numbers results in the average Nusselt number, which can also be determined with the following formula:
\begin{align}
\label{97}
&\boxed{\overline{Nu}= \sqrt[3]{83.326 + \left(1.953 \cdot \sqrt[3]{\overline{\beta}}-0.6 \right)^3} } \\[5px]
&\overline{\beta}=Re \cdot Pr \cdot \frac{d}{l}\\[5px]
\end{align}
Again, it should be noted that for long pipes the profile factors are close to zero. In these cases the Nusselt numbers approach the asymptote of 4.364 [see equation (\ref{4364})]:
\begin{align}
& \lim \limits_{l \to \infty}\beta \rightarrow 0 ~~~\Rightarrow~~~ Nu\rightarrow 4.364 \\[5px]
\end{align}
Taking into account the development of the flow (short pipes)
Even under the condition of constant heat flux, the development of the flow must again be taken into account, if such a development is present inside the pipe. For Prandtl numbers greater than 0.7, the following formulas can be used to calculate the local or average Nusselt number:
\begin{align}
&\boxed{\overline{Nu}= 0.924 \cdot Pr^{-\frac{1}{6}} \cdot \sqrt{\overline{\beta}}} ~&&\overline{\beta}=Re \cdot Pr \cdot \frac{d}{l}\\[5px]
&\boxed{Nu= 0.462\cdot Pr^{-\frac{1}{6}} \cdot \sqrt{\beta}} ~&&\beta=Re \cdot Pr \cdot \frac{d}{x}\\[5px]
&Pr>0.7
\end{align}
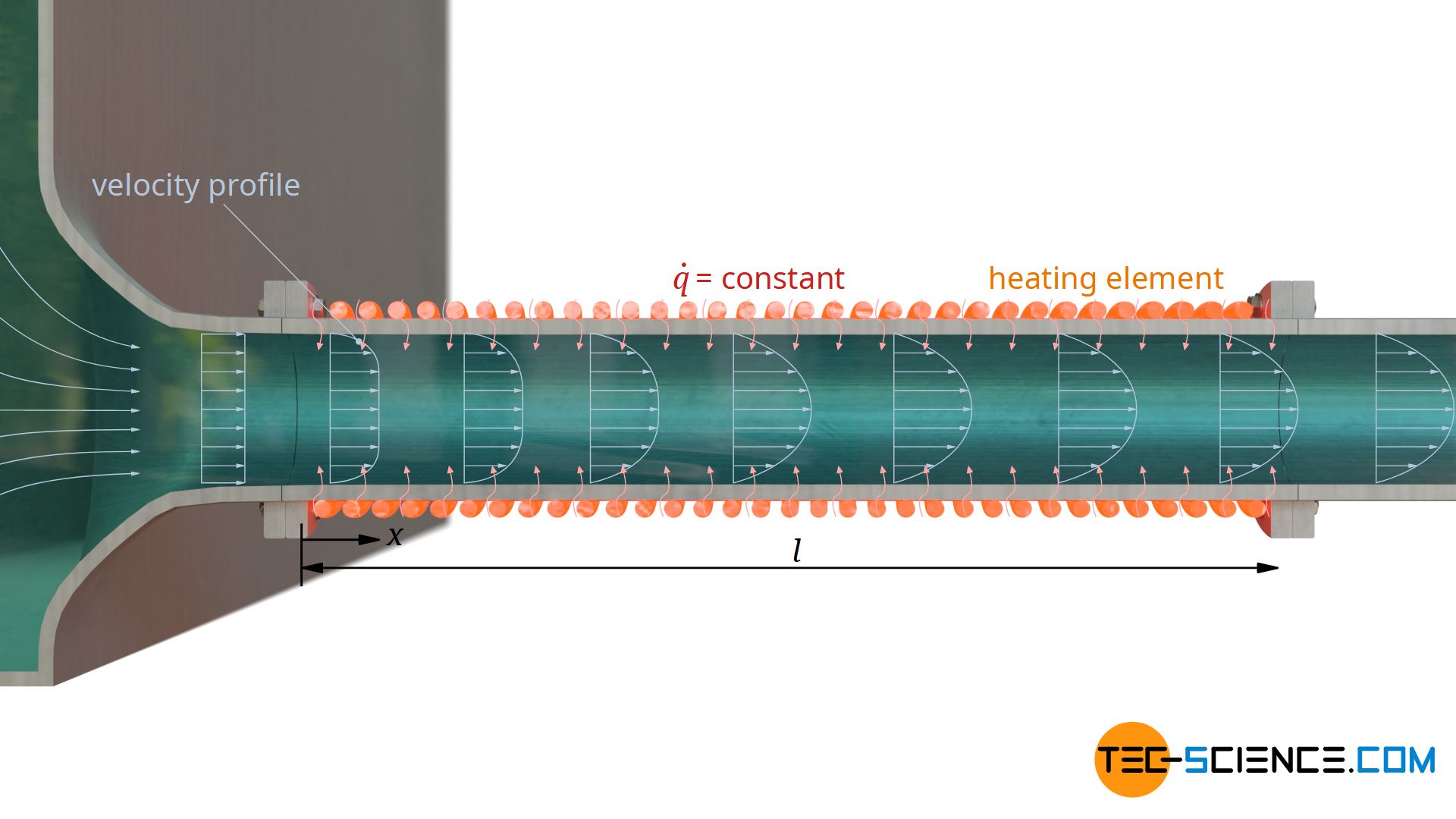
Again, the calculated Nusselt numbers for large values of x and l come closer and closer to the values from equation (\ref{96}) or (\ref{97}), since the influence of the inlet length becomes more and more negligible. However, as one can also see, the Nusselt numbers obtained by taking the development of the flow into account converge to zero for further increasing values of x or l. This makes little sense, however, because the limit for the Nusselt numbers is 4.364 according to the equation (\ref{4364}).
The formulas above are therefore only valid as long as they result in larger values than the calculations with the formulas (\ref{96}) or (\ref{97}). If smaller values are obtained, then the equations (\ref{96}) or (\ref{97}) are valid, even for not fully developed flows!
Taking into account the direction of the heat flow and the temperature dependence of the material properties
For liquids, the influence of the temperature-dependent material values on the average Nusselt number is again considered with a correction factor according to equation (\ref{temp}). For gases, the influence is usually negligible.
Turbulent flow
In turbulent flows, the fluid mixes very strongly at the wall, so that in practice it is not necessary to differentiate between the conditions of constant wall temperature and constant heat flux when calculating the Nusselt numbers.
In this context, the turbulence of the flow significantly influences the heat transfer and thus the Nusselt number. The roughness of the pipe wall plays a decisive role here, which in turn has an effect on the pressure loss along the pipe. The Nusselt number is therefore given as a function of the pressure loss coefficient ζ.
According to Gnielinski (Neue Gleichungen für den Wärme- und den Stoffübergang in turbulent durchströmten Rohren und Kanälen. Forschung im Ingenieurwesen 41, 1975) and Filonenko (Hydraulischer Widerstand von Rohrleitungen, 1954) the following formula can be used to calculate the average Nusselt number:
\begin{align}
&\boxed{\overline{Nu} = \frac{\frac{\zeta}{8} \cdot (Re-1000) \cdot Pr}{1+12.7 \cdot \sqrt{\frac{\zeta}{8}} \cdot (Pr^\frac{2}{3}-1 )} \cdot \left[1+\left(\frac{d}{l}\right)^\frac{2}{3}\right]} \\[5px]
&~~~\boxed{\zeta=\left(1.82\cdot \log_{10}(Re) -1.64\right)^{-2}} \\[5px]
\end{align}
If pressure loss coefficients are not known, the following formulas can also be used for approximate calculations for the average Nusselt numbers:
\begin{align}
&\boxed{\overline{Nu} = 0.0214 \left(Re^{0.8}-100 \right)\cdot Pr^{0.4}\cdot \left[1+\left(\frac{d}{l}\right)^\frac{2}{3} \right]} ~~~0.5<Pr<1.5\\[5px]
&\boxed{\overline{Nu} = 0.0120 \left(Re^{0.87}-280\right)\cdot Pr^{0.4}\cdot \left[1+\left(\frac{d}{l}\right)^\frac{2}{3} \right]} ~~~1.5<Pr<500\\[5px]
\end{align}
The dependence of the material values on the temperature can in turn be taken into account for liquids by the ratio of the Prandtl numbers at the mean temperature (Pr) and the wall temperature (Prw):
\begin{align}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{Pr}{Pr_w}\right)^{0.11} } ~ \text{valid for liquids}\\[5px]
\end{align}
For gases, the Prandtl numbers are only slightly dependent on temperature. The temperature influence on the heat transfer is therefore taken into account directly via the relationship between mean gas temperature Tm and wall temperature Tw:
\begin{align}
&\boxed{\overline{Nu}^*= \overline{Nu} \cdot \left(\frac{T_m}{T_w}\right)^{n} } ~ \text{valid for gases}\\[5px]
\end{align}
\begin{align}
&n=0 && \text{für}~~ T_m>T_w ~\text{(gas is cooled down by the wall)}\\[5px]
&n\neq 0 && \text{für}~~T_w>T_m ~\text{(gas is heated by the wall)}\\[5px]
\end{align}
If the gas transfers heat to the wall, i.e. the gas is cooled, the influence of temperature on the Nusselt number is relatively small. The exponent is therefore zero (n=0). In the case that the wall transfers heat to the gas, i.e. the gas is heated, the exponent is strongly dependent on the type of gas. The exponent can be either positive or negative depending on the pressure and temperature.






