Viscosity of liquids and gases

The viscosity of a fluid is a measure of the internal resistance to flow! It is caused by intermolecular forces and transport of momentum within the fluid.

Introduction

If one looks at the flow behavior of water in comparison to honey, large differences are noticeable. If one pours these substances for example on an inclined plane, then honey flows clearly more slowly than water. Honey shows so to speak a high flow resistance, is thus less flowable. This characteristic of the flow resistance is called viscosity in the technical language.

Not only liquids show a viscous behavior, but also gases. With gases the viscosity is however less pronounced. Such viscous substances such as liquids and gases are also generally referred to as fluids (lat. fluidus for “to flow”).

Viscosity is a measure of the internal flow resistance of a fluid!

Derivation of viscosity

How can viscosity be described mathematically? First of all, it makes sense to think about what the actual cause of viscosity is. One can imagine the fluid for this purpose as being composed of many small layers. Due to the intermolecular forces of attraction of the molecules, these layers adhere to each other. These attractive forces act like frictional forces, which are one of the reasons for the viscous behavior of the fluid. The viscosity is therefore often referred to as internal friction. For this reason, each layer prevents the adjacent fluid layer from flowing. The viscosity can therefore be formulated more precisely:

The viscosity is a measure of the strength of adhesion between the fluid layers!

Viscosity can thus be defined by the force required to move these imaginary fluid layers against each other. For this purpose, the fluid is thought to be enclosed between two horizontal plates. The lower plate is fixed and the upper plate is movable. When the upper plate is moved, the fluid layers must be sheared off against each other. This requires a more or less strong force depending on the viscosity. The variables influencing this force are explained below. Such a flow between two surfaces moving relative to each other is also called Couette flow.

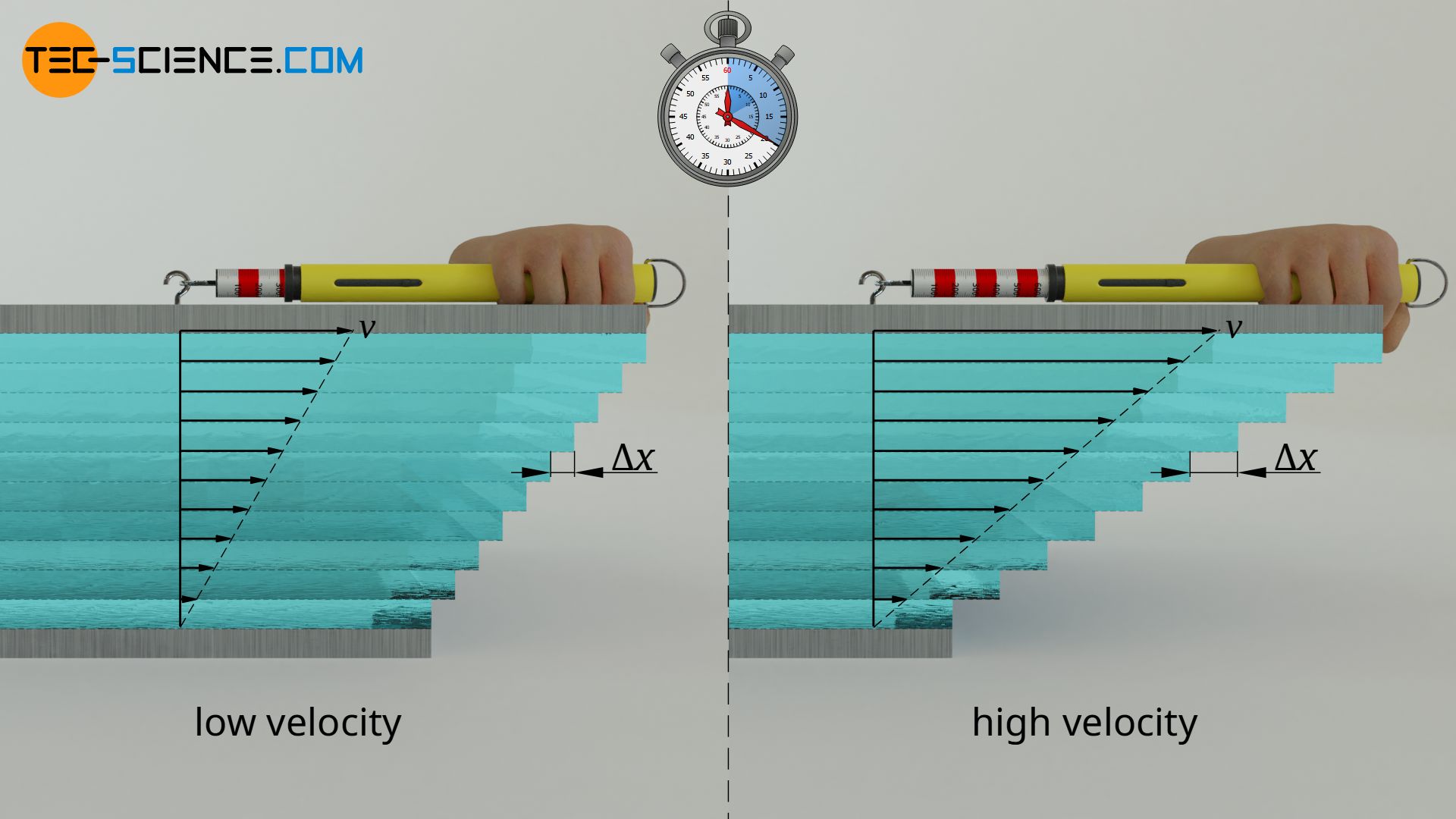
Influence of speed

Not only within the fluid act forces (cohesion), but also between fluid and wall (adhesion). The fluid thus sticks at both plates. This is also called no-slip condition. At the downside plate thus the speed of fluid layer is zero and increases linear up to speed of the upper plate. The higher the speed of the upper plate, the more the fluid layers must obviously be shifted against each other per time unit and the higher the force required for this is.

Binding forces within a substance are called cohesion, while binding forces between two different substances are called adhesion!

Theoretically, in addition to the upper plate, the lower plate could also move at a certain speed. In this general case, the difference in velocity Δv of the two plates determines the force F. Within certain limits, a proportional relationship can be seen:

\begin{align}
& F \sim \Delta v \\[5px]
\end{align}

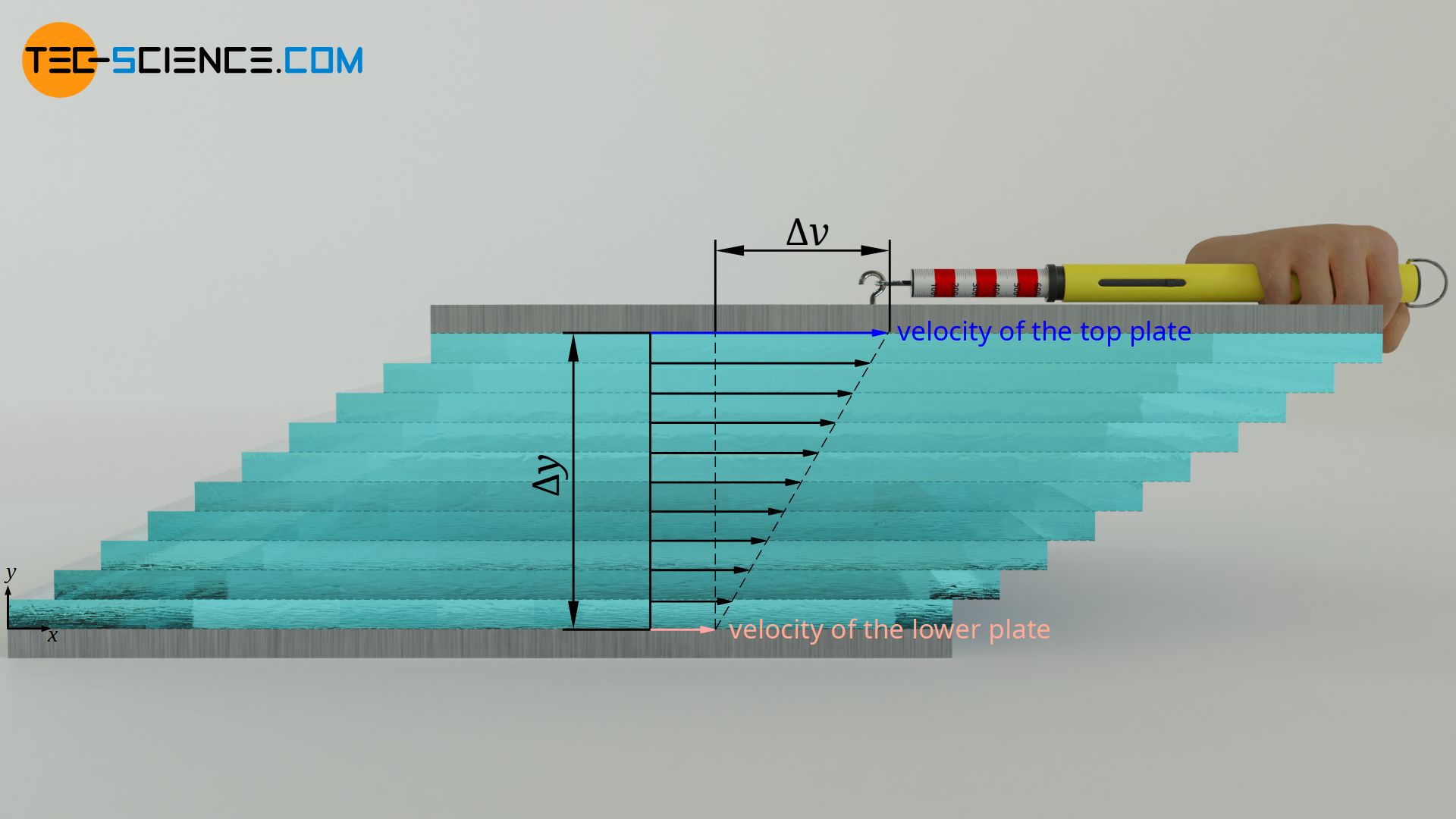
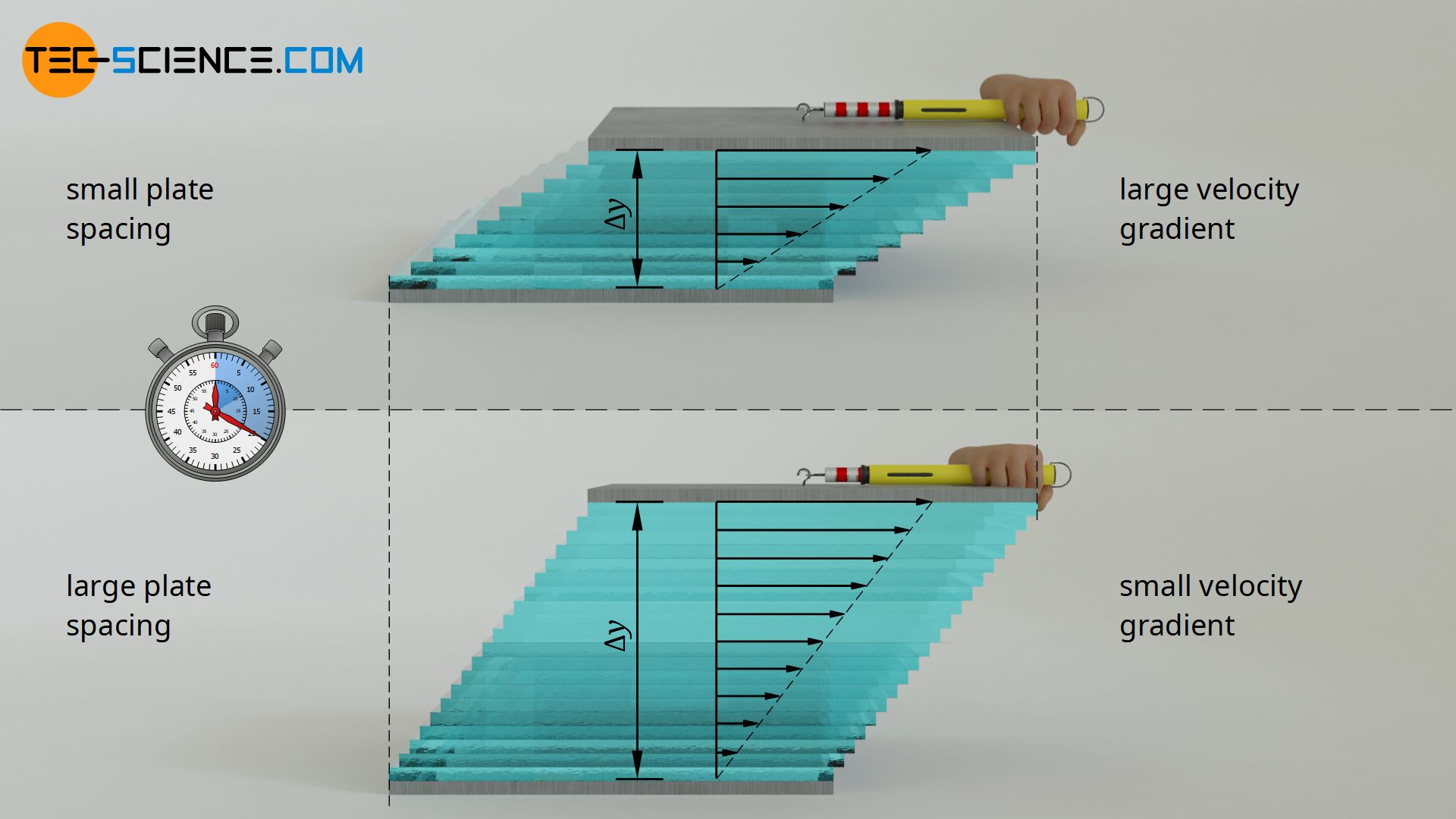
Influence of the distance between the plates (thickness of the fluid)

The magnitude of the displacement and thus the force, however, is not only determined by the difference in speed, but also by the distance between the plates. The greater the distance for a given speed difference, the smaller the displacement of the individual fluid layers per time unit. There is a reciprocal relationship between plate distance Δy and displacement or force F:

\begin{align}
& F \sim \frac{1}{\Delta y} \\[5px]
\end{align}

Influence of the area of the plate

The required force is also influenced by the surface area of the plate or the area the fluid layers. The larger the area, the more bonds are obviously present between the individual fluid layers and the greater the force required to move the fluid layers against these bonding forces. Required force F and area A are proportional to each other, because after all, twice the area means twice the number of bonds:

\begin{align}
& F \sim A \\[5px]
\end{align}

Newton’s law of fluid motion

The force F required to displace the fluid layers against each other, is thus proportional to the velocity difference Δv and the fluid area A, and inversely proportional to the thickness of the fluid layer Δy. The following qualitative relationship therefore applies to the required force:

\begin{align}
& F \sim A \cdot \frac{\Delta v}{\Delta y}\\[5px]
& \underbrace{\frac{F}{A}}_{\tau} \sim \underbrace{\frac{\Delta v}{\Delta y}}_{\dot \gamma}\\[5px]
&\tau \approx \dot \gamma \\[5px]
\end{align}

The quotient on the left side of the equation describes the force per unit area required to shear the fluid layers against each other. This quantity is therefore also called shear stress τ. The quotient on the right side describes the change in speed in the fluid per unit length (perpendicular to the direction of fluid motion), i.e. the so-called velocity gradient. This velocity gradient is often also referred to as shear rate γ* because it describes the speed with which the individual layers move relative to each other.

\begin{align}
&\boxed{\tau:=\frac{F}{A}} ~~~\text{ shear stress} \\[5px]
&\boxed{\dot\gamma:=\frac{\Delta v}{\Delta y}} ~~~\text{ shear rate (velocity gradient)} \\[5px]
\end{align}

The stress required to shear the fluid off is therefore proportional to the shear rate. The proportionality constant between these quantities is finally called (dynamic) viscosity η. The unit of viscosity is Pa·s (Pascal second), whereas for liquids and gases the unit mPa·s (millipascal second) is usually used due to the low viscosities. The proportional relationship between shear rate and shear stress is also known as Newton’s law of fluid motion. Fluids that satisfy this law are called Newtonian fluids (more about this later).

\begin{align}
\label{t}
&\boxed{\tau= \eta \cdot \dot \gamma} ~~~[\eta]=\frac{\text{N}\cdot\text{s}}{\text{m²}}=\text{Pa}\cdot\text{s} ~~~~~\text{Newton’s law of fluid motion}\\[5px]
\end{align}

Consequently, higher viscosity values mean greater shear stress required to shear the fluid layers against each other and the greater the internal flow resistance of the liquid.

The (dynamic) viscosity describes the mathematical relationship between shear rate and shear stress of fluids. This is also known as Newton’s law of fluid motion.

The definition of viscosity presumes that the movement of the fluid can be divided into individual layers that shift against each other. Such a “layered flow” is also called laminar flow. However, at high flow velocities, turbulence is formed in the fluid and the flow becomes turbulent. In this case, however, the definition of a viscosity makes no sense. The validity of the viscosity is therefore limited to laminar flows. More information about laminar and turbulent flows can be found in the article Reynolds number (laminar and turbulent flow).

Temperature dependence of viscosity

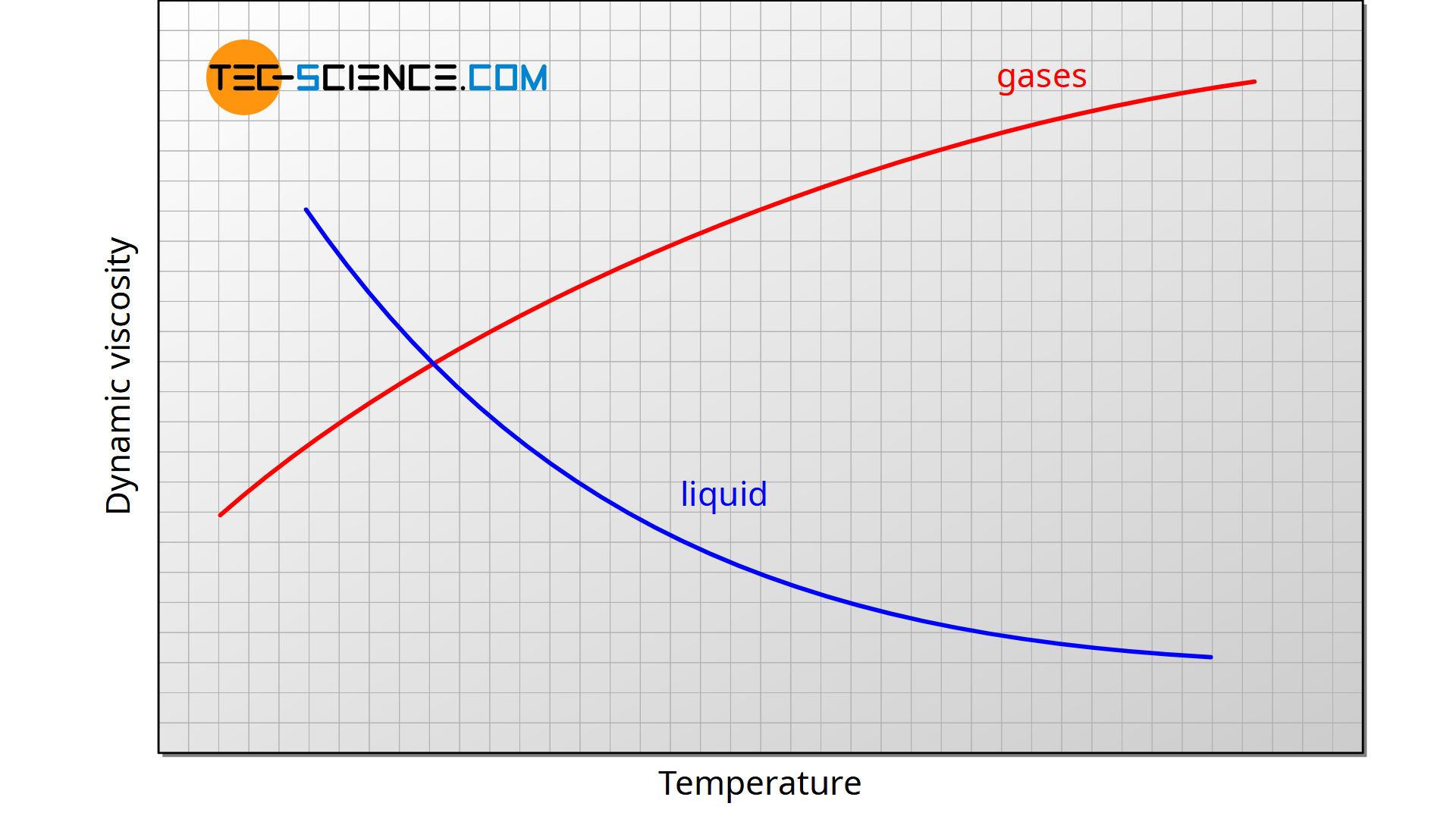
The viscosity is generally pressure and above all temperature dependent. With liquids, viscosity decreases with increasing temperature. This behavior is very clearly shown with honey or butter, for example. If these substances are heated, they become more flowable, almost like “real” liquids, i.e. the viscosity decreases. But also water shows a pronounced temperature dependence. For example, water has a viscosity of 1.5 mPa·s at 5°, at 20 °C the viscosity has decreased by a third to 1.0 mPa·s.

This phenomenon can be explained by the increase in atomic spacing due to thermal expansion, which is associated with an increase in temperature. If the atomic spacings increase due to an increase in temperature, the intermolecular forces of attraction decrease. You can illustrate the situation with two magnets. At small distances the magnets attract each other relatively strongly. With increasing distance, the attractive forces decrease. Although the atomic forces are not magnetic forces, but electrostatic forces, the laws are similar in both cases. Transferred to the atoms of a fluid, this means that the fluid layers no longer adhere so strongly to each other as the distance between the molecules increases.

For Newtonian fluids, the temperature dependence can be described in good approximation mostly by an exponential function. In principle, this also applies to the pressure dependence, which only plays a noticeable role at high pressures. The following equation is a good approximation of the temperature dependence. In it, η₀ denotes a fictitious reference viscosity and “a” and “b” constants, and T denotes temperature (H. Vogel: Das Temperaturabhängigkeitsgesetz der Viskosität von Flüssigkeiten. 1921).

\begin{align}
&\boxed{\eta(T) \approx \eta_0 \cdot \text{e}^{\left( \LARGE \frac{a}{T+b}\right)}}~~~\text{valid for liquids} \\[5px]
\end{align}

Gases usually show a different relationship between viscosity and temperature. For these substances, the viscosity generally increases with rising temperature. This is due to the increased exchange of momentum between the individual gas layers, which determines the viscosity in addition to the intermolecular attraction forces. With liquids, this exchange of momentum plays a subordinate role, which is why it does not have a decisive influence on the viscosity of liquids. More detailed information can be found in the article Viscosity of an ideal gas.

For gases, the dependence of viscosity can be described with the following equation. In this equation η₀ denotes the reference viscosity at a reference temperature T₀ and c a substance-dependent Sutherland constant (W. Sutherland: The Viscosity of Gases and Molecular Force. 1893).

\begin{align}
&\boxed{\eta(T) \approx \eta_0 \cdot \frac{T_0+c}{T+c}\cdot \left(\frac{T}{T_0}\right)^\frac{3}{2}}~~~\text{valid for gases} \\[5px]
\end{align}

Formulas for calculating the viscosity of air and water

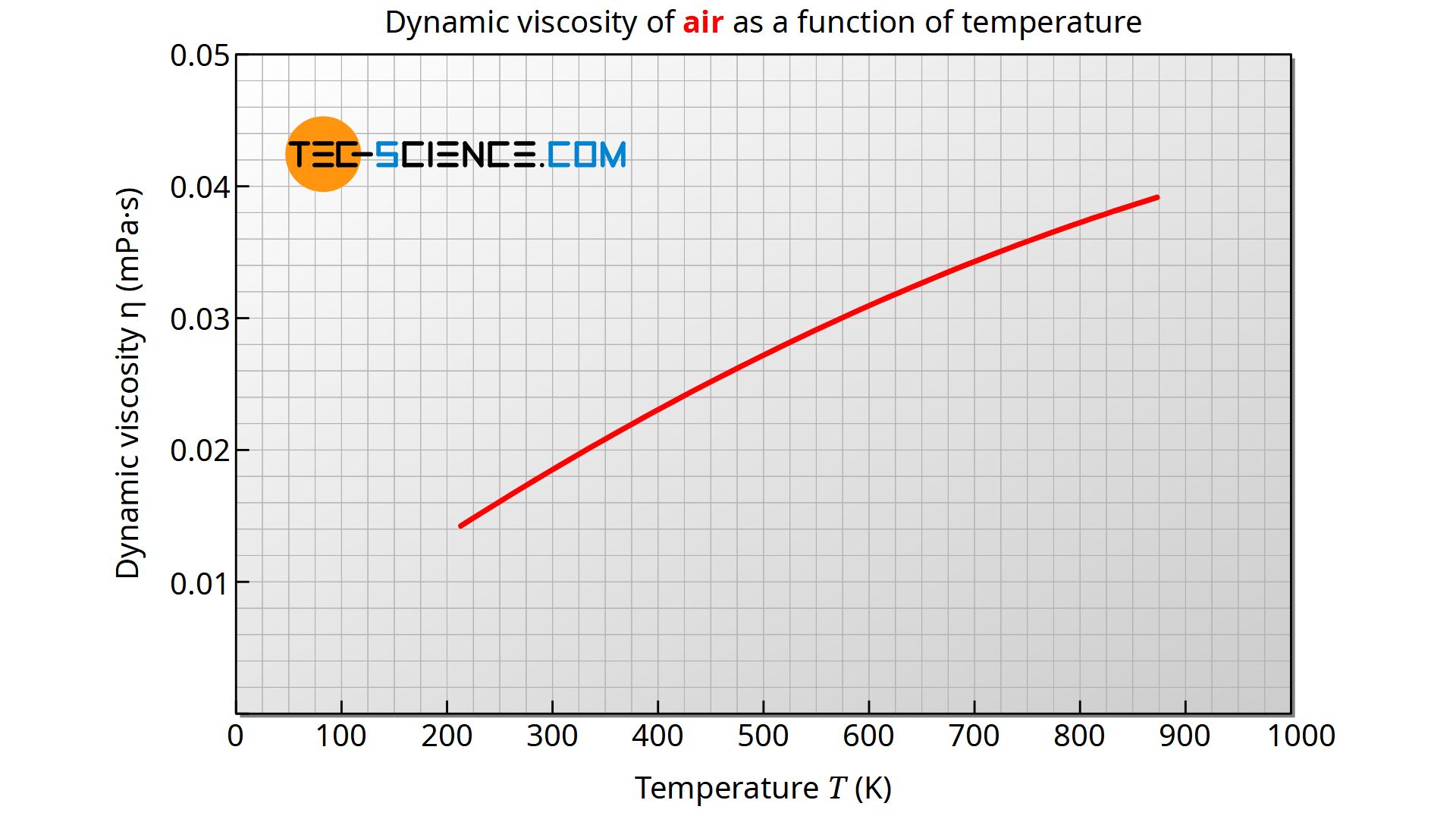
In many practical cases, the flowing fluids are air (e.g. in wind tunnels) or water (e.g. in pipes). For air at 1 bar pressure, the dynamic viscosity in the temperature range between -20 °C and 400 °C can be determined in good approximation using the formula given below. The deviations from the literature values are less than 1 %. The temperature shall be used in the unit Kelvin to calculate the viscosity in the unit Pa·s.

\begin{align}
&\boxed{\eta_{\text{air}}(T) = 2.791\cdot 10^{-7} \cdot T^{0.7355}}~~~\text{Pa·s} \\[5px]
\end{align}

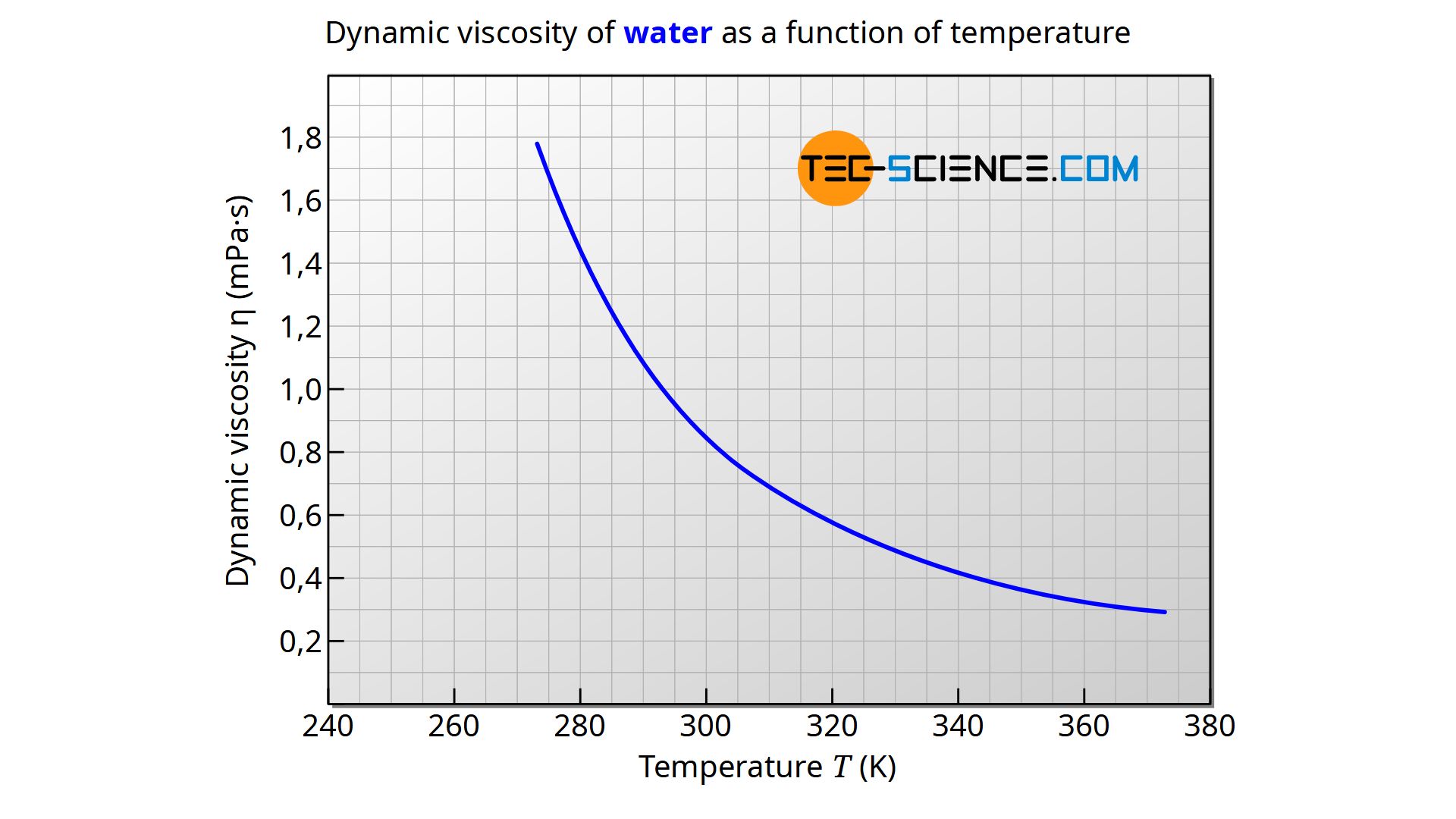
The dynamic viscosity of water at 1 bar pressure can be determined in the temperature range between 0 °C and 100 °C with a deviation of less than 1 % from the literature values using the formula given below. The temperature must be used in the unit Kelvin, so that the result is given in the unit Pa·s.

\begin{align}
&\boxed{\eta_{\text{water}}(T) = \frac{1}{0.1\cdot T^2-34.335 \cdot T+2472}}~~~\text{Pa·s} \\[5px]
\end{align}

The decreasing viscosity at elevated temperature can even be “heard” in the case of water! If you pour cold water into a glass, the tone is significantly higher than with hot water. The cause is the lower viscosity of the hot water, which leads to larger bubbles when pouring. The size of these bubbles in turn affects the sound, so that cold water with a higher viscosity is audibly different from hot water with a lower viscosity.

Dynamic and kinematic viscosity

When talking about viscosity, this usually means the dynamic viscosity η as defined in the previous section. The flow behavior of liquids or gases are not only determined by the viscosity of a fluid, but also by its density. For the characterization of the flow behavior it is therefore useful to consider the viscosity in relation to the density. If the viscosity is related to the density of the fluid, then we also speak of kinematic viscosity ν (Greek small letter Nu). The unit of kinematic viscosity is m²/s.

\begin{align}
&\boxed{\nu= \frac{\eta}{\rho}} ~~~\text{ kinematic viscosity} ~~~[\nu]=\frac{\text{m²}}{\text{s}} \\[5px]
\end{align}

The kinematic viscosity puts the viscosity of a fluid in relation to its density and is a measure of how “pasty” a fluid is. It is determined by the quotient of dynamic viscosity and density!

A high kinematic viscosity means that the fluid has a very high viscosity compared to its density. Colloquially one would say that the fluid behaves relatively pasty. In contrast to dynamic viscosity, kinematic viscosity is relatively strongly dependent on pressure even at low pressures, especially in the case of compressible gases.

As already indicated, the kinematic viscosity plays a major role in the flow behavior of a fluid. It is a decisive factor in determining how susceptible a flowing fluid is to turbulence. It therefore has a great influence on the speed at which a fluid changes from laminar flow to turbulent flow (see article Reynolds number (laminar and turbulent flow)).

Note on terminology: The kinematic viscosity describes the flow behavior, i.e. the kinematics of the flow. Dynamic viscosity, on the other hand, describes the acting forces, i.e. the dynamics of the flow.

Newtonian and non-Newtonian fluids

For many fluids, the viscosity is actually a material constant in very good approximation, which is only dependent on temperature and pressure. For such Newtonian fluids, the viscosity and thus the flow behavior is independent of the shear rate. In a diagram showing the relationship between shear stress and shear rate, a straight line through the origin is obtained. According to equation (\ref{t}), the slope of this line corresponds to the viscosity of the fluid and this is constant in every point. Water, gases and many oils can be regarded as such Newtonian fluids.

With Newtonian fluids, the flow behavior (viscosity) is constant regardless of the shear rate!

However, there are also fluids whose viscosity depends on the shear rate. The flow behavior of such non-Newtonian fluids changes depending on the shear rate. Blood, ketchup and toothpaste, for example, are among them. Since the viscosity is no longer a constant for such substances, the flow behavior can no longer be described by equation (\ref{t}).

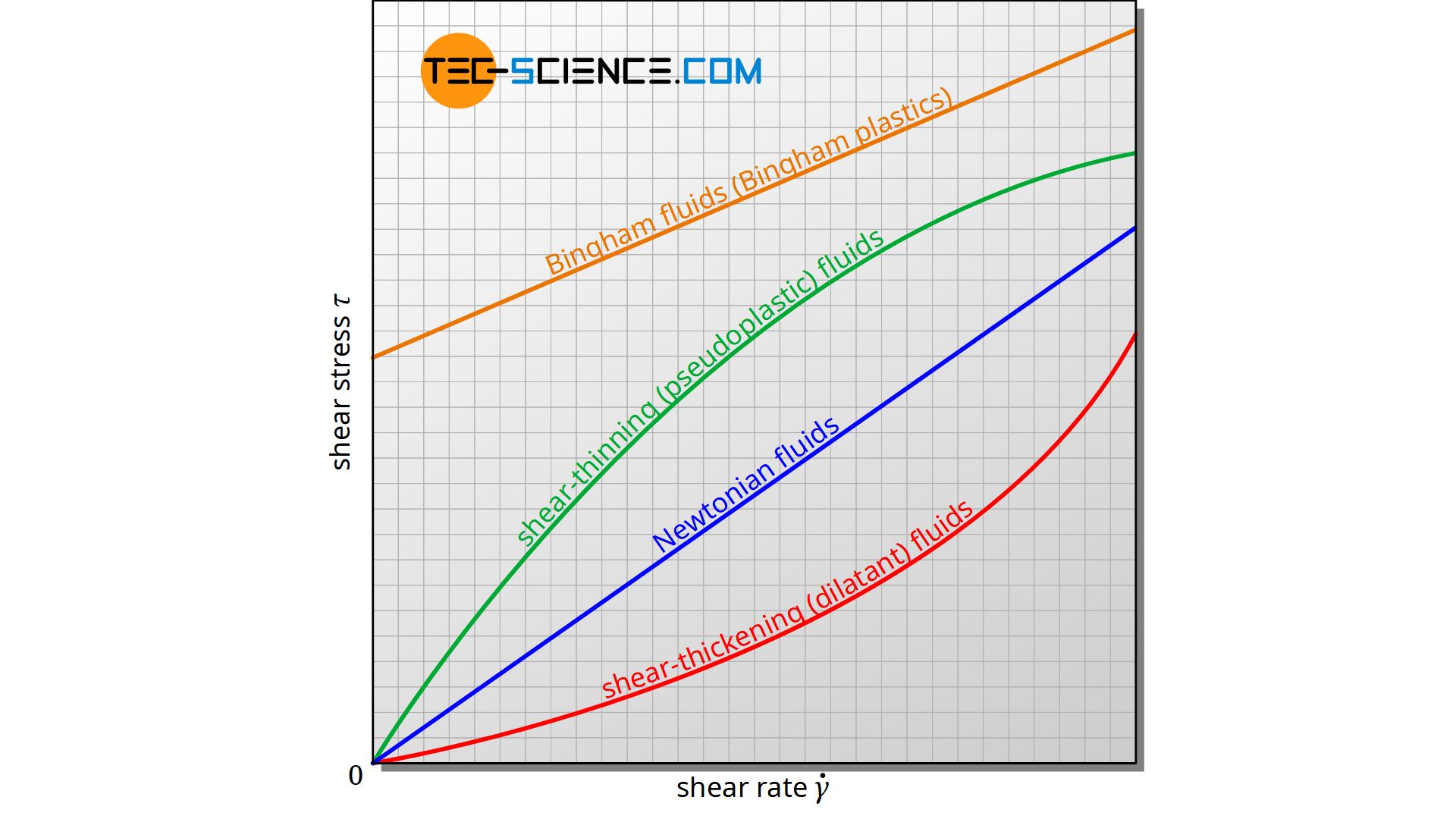
Shear-thickening (dilatant) fluids

If the flow resistance of a fluid increases with increasing shear rate, the fluid behaves more viscous, so to speak. This is why we speak of a shear-thickening fluid. Such a fluid is also called a dilatant fluid. The increasingly viscous flow behavior of such a fluid is shown in the diagram as an increasingly steeper rising curve.

Shear-thickening (dilatant) fluids show an increase in flow resistance with increasing shear rate!

A dilatent fluid can be produced relatively easily at home. For this you add about 2 parts of water to about 3 parts of starch and mix it well. If you now slowly move a spoon through this slurry (low shear rate), the mixture behaves relatively liquid. However, if you try to move the spoon very quickly through the mixture (high shear rate), it will thicken and partly begins to crumble like a solid. The crumbled parts then become liquid again.

Dilatancy can be described mathematically with the following approach. In this equation, K and n are material-based constants, whereby the flow index n is greater than 1.

\begin{align}
\label{d}
&\boxed{\tau= K \cdot \left(\frac{\text{d}v}{\text{d}y}\right)^n} \\[5px]
\end{align}

Shear-thinning (pseudoplastic) fluids

Conversely, we speak of a shear-thinning fluid if the fluid behaves more fluid with increasing shear rate, i.e. the viscosity decreases. Such a fluid is also called a pseudoplastic fluid. In the diagram, the curve of such a fluid becomes increasingly flatter.

Shear-thinning (pseudoplastic) fluids show a decrease in flow resistance with increasing shear rate!

An example of a shear-thinning fluid is quicksand. This is what makes quicksand so dangerous, because if you panic and make rapid movements, the water-sand mixture liquefies and you sink in very quickly. In this case it is better to stay as calm as possible and only make slow movements. Blood is also one of the shear-thinning fluids.

The flow behavior of pseudoplastic fluids can also be described with equation (\ref{d}), whereby in these cases the flow index n is less than 1. By the way, this equation also applies to Newtonian fluids with a flow index of n=1 and K as dynamic viscosity!

Bingham Fluids

However, there are also fluids that require a certain minimum shear stress in order to shear the fluid layers off in the first place. Below this minimum shear stress the fluid does not start to flow. Such fluids are also known as Bingham fluids oder Bingham plastics. Examples are toothpaste, mayonnaise or ketchup.

Bingham plastics require a minimum shear stress to make the fluid flow!

In the case of a toothpaste, such a flow behavior becomes very clear. If you turn the toothpaste tube upside down, it will not run out of the opening by itself. You first need a certain minimum force by pressing the tube so that the toothpaste flows out. Even when trying to get ketchup out of a glass bottle, it turns out that simply turning the bottle upside down is usually not enough. First you have to tap the bottom of the bottle with your hand, i.e. apply a minimum shear stress so that the ketchup flows out.

Bingham plastics can be represented in the diagram as a curve with a y-intercept τ₀ (minimum shear stress). They can be described by the following equation, with n as the flow index (n=1 for a straight line):

\begin{align}
\label{b}
&\boxed{\tau= K \cdot \left(\frac{\text{d}v}{\text{d}y}\right)^n + \tau_0} \\[5px]
\end{align}