The Lewis number is a dimensionless similarity parameter to describe heat and mass transport.
The Lewis number always comes into play when a flowing fluid is transferring both heat by conduction and mass by diffusion (diffusion of heat and mass, so to speak). The Lewis number puts the thickness of the thermal boundary layer in relation to the concentration boundary layer. It is determined from the ratio of the thermal diffusivity “a” and the diffusion coefficient D:
\begin{align}
&\text{Lewis number}= \frac{\text{transport of heat}}{\text{transport of mass}} \\[5px]
\label{le}
&\boxed{Le = \frac{a}{D}}=\frac{\lambda}{D \cdot c_p \cdot \rho} \\[5px]
\end{align}
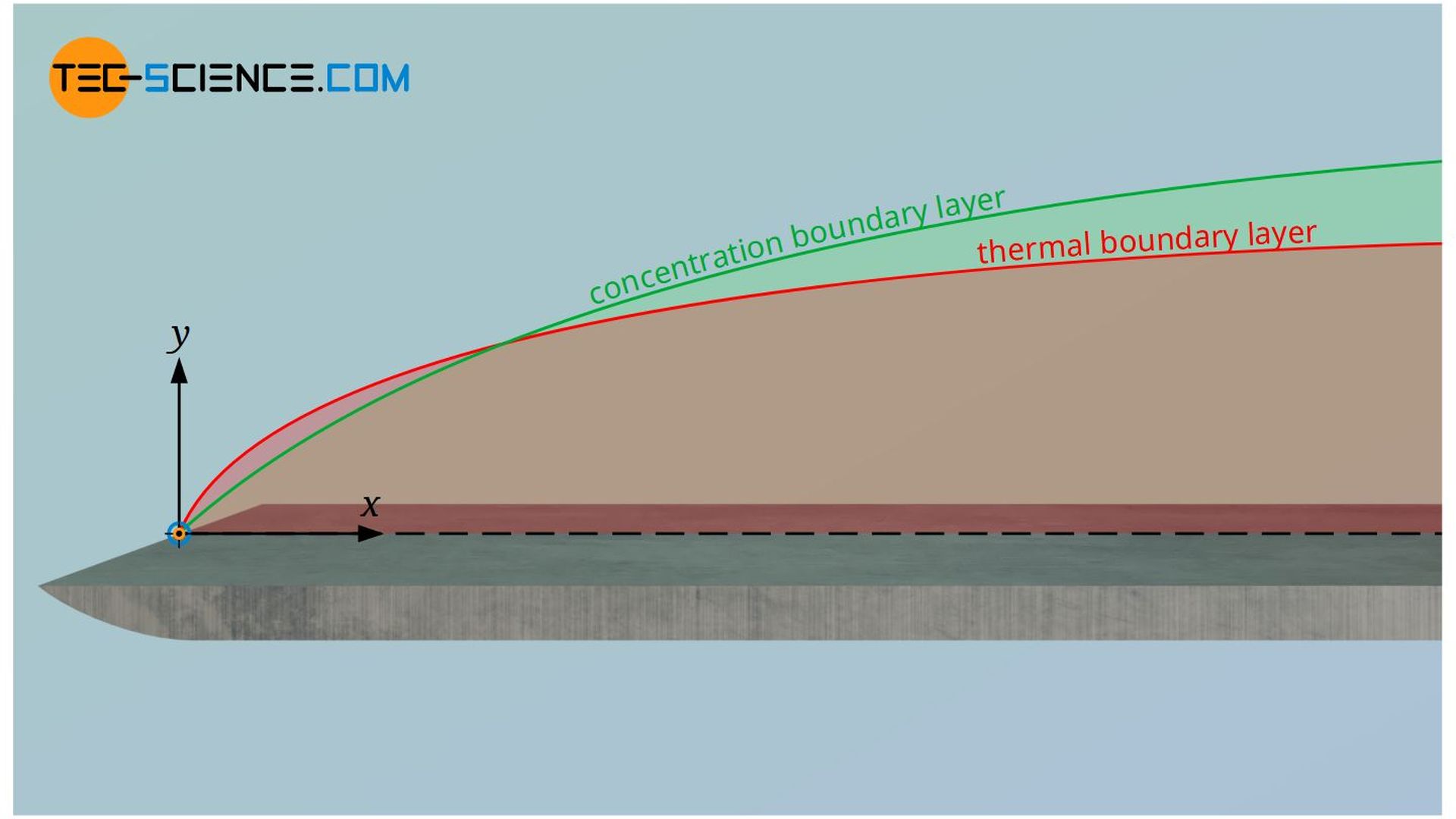
Since the thermal diffusivity can by definition be calculated from the thermal conductivity λ, the density ϱ and the isobaric specific heat capacity cp, the Lewis number can also be determined with these quantities. Furthermore, the Lewis number can also be determined from the ratio between the Schmidt number Sc and the Prandtl number Pr:
\begin{align}
&\boxed{Le = \frac{Sc}{Pr}} \\[5px]
\end{align}
Heat and mass transfer are physically similar in systems of different sizes only if the Lewis numbers are identical. In this way, it is possible to make statements for the real system on the basis of scaled-down models.
In the table below the three important dimensionless similarity parameters are summarized. In the article Dimensionless numbers of the boundary layers, the parameters are explained in more detail.
| Prandtl number Pr | Schmidt numer Sc | Lewis number Le |
| Ratio of momentum transport to energy transport | ratio of momentum transport to mass transport | ratio of heat transport to mass transport |
| \begin{align} \notag &\boxed{Pr = \frac{\nu}{a}}=\frac{\eta \cdot c_p}{\lambda} \\[5px] \end{align} | \begin{align} \notag &\boxed{Sc = \frac{\nu}{D}} =\frac{\eta}{\rho \cdot D}\\[5px] \end{align} | \begin{align} \notag &\boxed{Le = \frac{a}{D}}=\frac{\lambda}{\rho \cdot c_p \cdot D} \\[5px] \end{align} |






