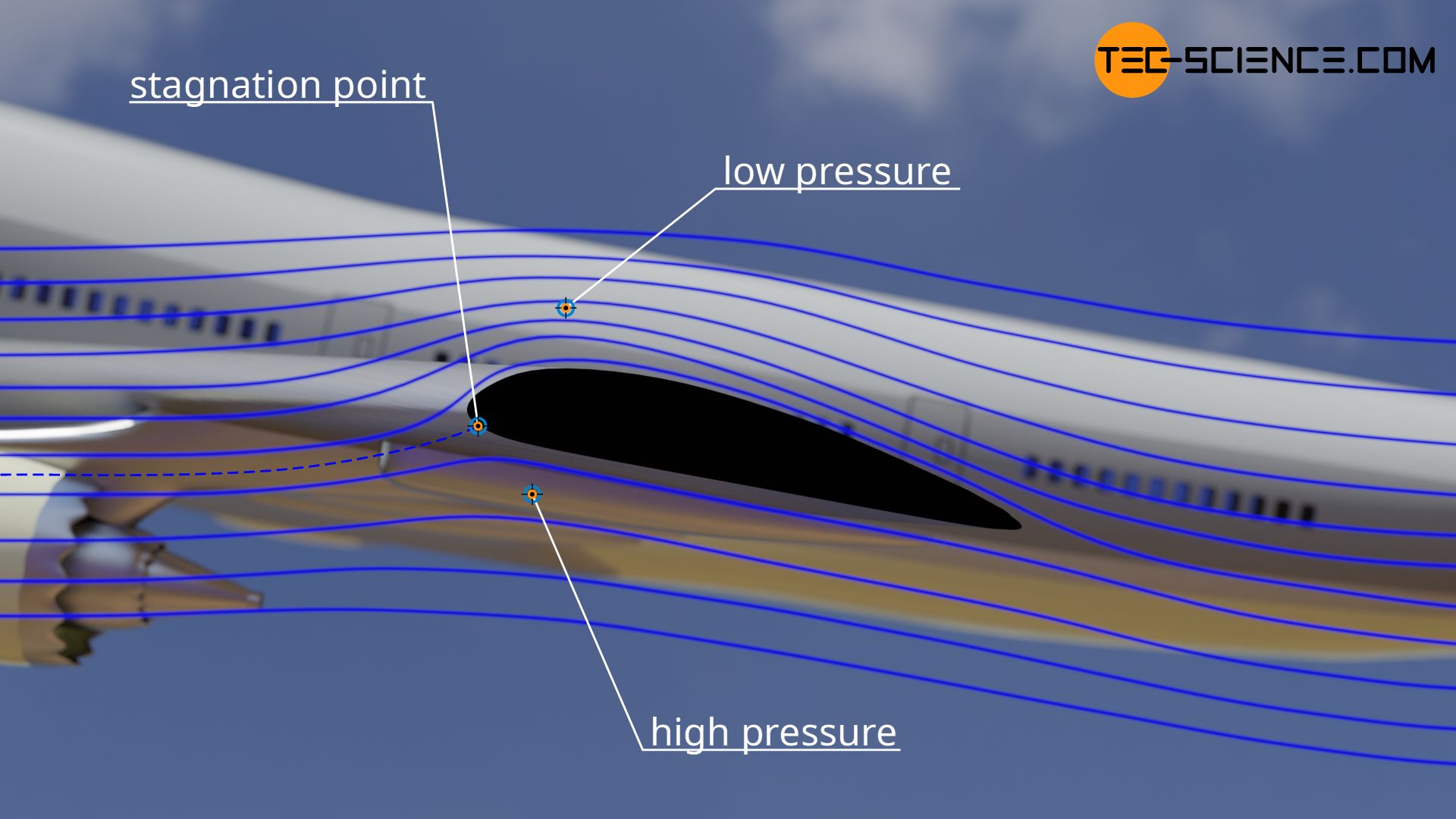
Drag is the force of resistance that a moving body experiences in a fluid due to frictional and pressure forces.
Introduction
In the article on boundary layers, it was explained, using the example of a plate with a flow around it, that shear stresses act within the hydrodynamic boundary layer. These lead to a deceleration of the fluid; directly at the wall even to a complete standstill. A typical velocity profile is formed within the boundary layer.
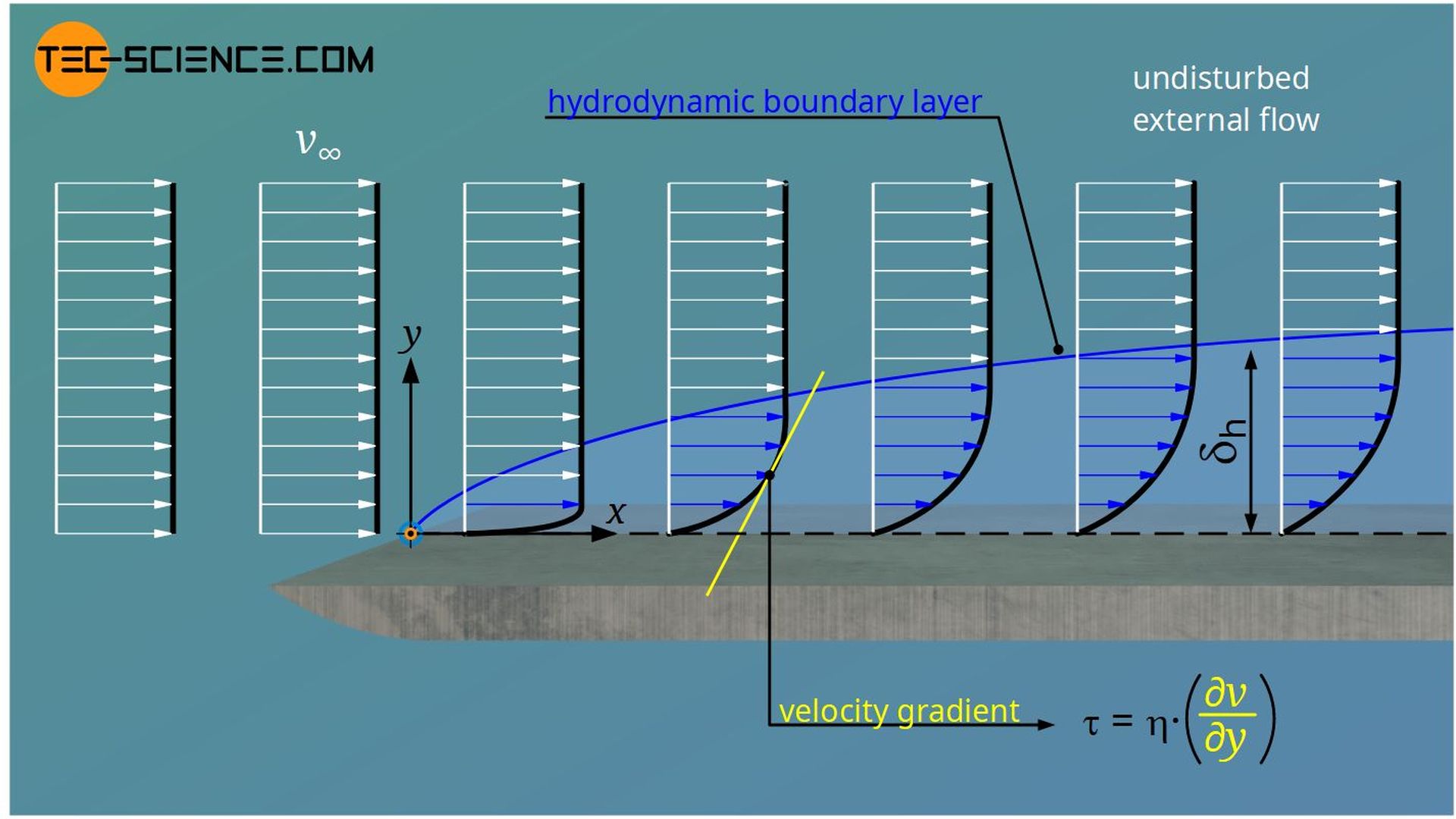
Now we turn the situation around in our minds. Instead of letting the fluid flow around the stationary plate, we now move the plate through a fluid at rest. Because of the shear stress, the fluid now tries to slow down the plate. The processes involved are described in more detail in the following sections.
A closer look reveals that it does not matter whether it is a resting object around which a fluid flows or a resting fluid through which an object is moved. One can imagine a camera fixed to the moving object and recording how the object moves through the fluid. If you look at the recorded video, you end up with exactly the same situation as with a stationary object with a fluid flowing around it. The fact that the two perspectives are identical is exploited in wind tunnels, for example. There it is not the model of an airplane that is moved through the resting air, but the air is moved around the stationary model.

Skin friction drag (shear stress drag)
Let us now look at the plate mentioned above, which moves through a resting fluid at constant speed. Again it is true that the fluid adheres directly to the plate due to the no-slip condition. The adhesive fluid layer consequently moves with the plate. However, this fluid layer also adheres to the fluid layer above it. Thus the adherent fluid layer is slowed down and with it the plate itself. In the case of air, this frictional force is known as air resistance (although there is another force that plays a role, which we will discuss later).
The occurrence of the frictional force can also be explained as follows. The adherent fluid layer is connected to the fluid layer above by intermolecular forces. If the plate is moved through the fluid, the entire (initially resting) fluid layers are gradually set in motion. This acceleration of the fluid layers requires a certain force. This force must be applied continuously, since new fluid layers must be set in motion again and again if the plate is to be moved through the surrounding fluid at a constant speed. This force to be applied corresponds to the frictional force mentioned in the previous argumentation – it is just another point of view.
Wall shear stress
For the frictional force that is exerted on the plate by the fluid, the shear stresses directly on the wall are decisive. This is because they ultimately indicate the tangential force that acts per unit area between the fluid and the solid surface. In this case one also speaks of the wall shear stress. The frictional force is therefore also called shear stress drag. For Newtonian fluids, the wall shear stress τw can be determined using Newton’s law of fluid friction:
\begin{align}
&\boxed{\tau_w = \eta \cdot \left(\frac{\partial v_x}{\partial y}\right)_\text{wall}}
\end{align}
Besides the viscosity of the fluid η, the velocity gradient of the flow ∂v/∂y|wall, which is directly present at the wall, is obviously of great importance. The gradient is mainly determined by the processes taking place in the boundary layer. Thereby it is decisive whether the boundary layer is laminar or turbulent. The figure below shows the flow around a plate where the laminar flow becomes unstable and thus turbulent.

The skin friction drag (viscous drag) of a body around which flow passes is due to the viscosity of the fluid and the associated wall shear stress!
Influence of the type of flow on the wall shear stress
In the article on the Hydrodynamic boundary layer it has already been explained in detail that the velocity profile increases more steeply with turbulent boundary layers, since vortices leads to an increased transfer of momentum between the fluid layers. This means in particular that the velocity gradient at the wall is greater than in a laminar flow. The figure below shows the velocity profile in the laminar flow and in comparison in the turbulent flow.
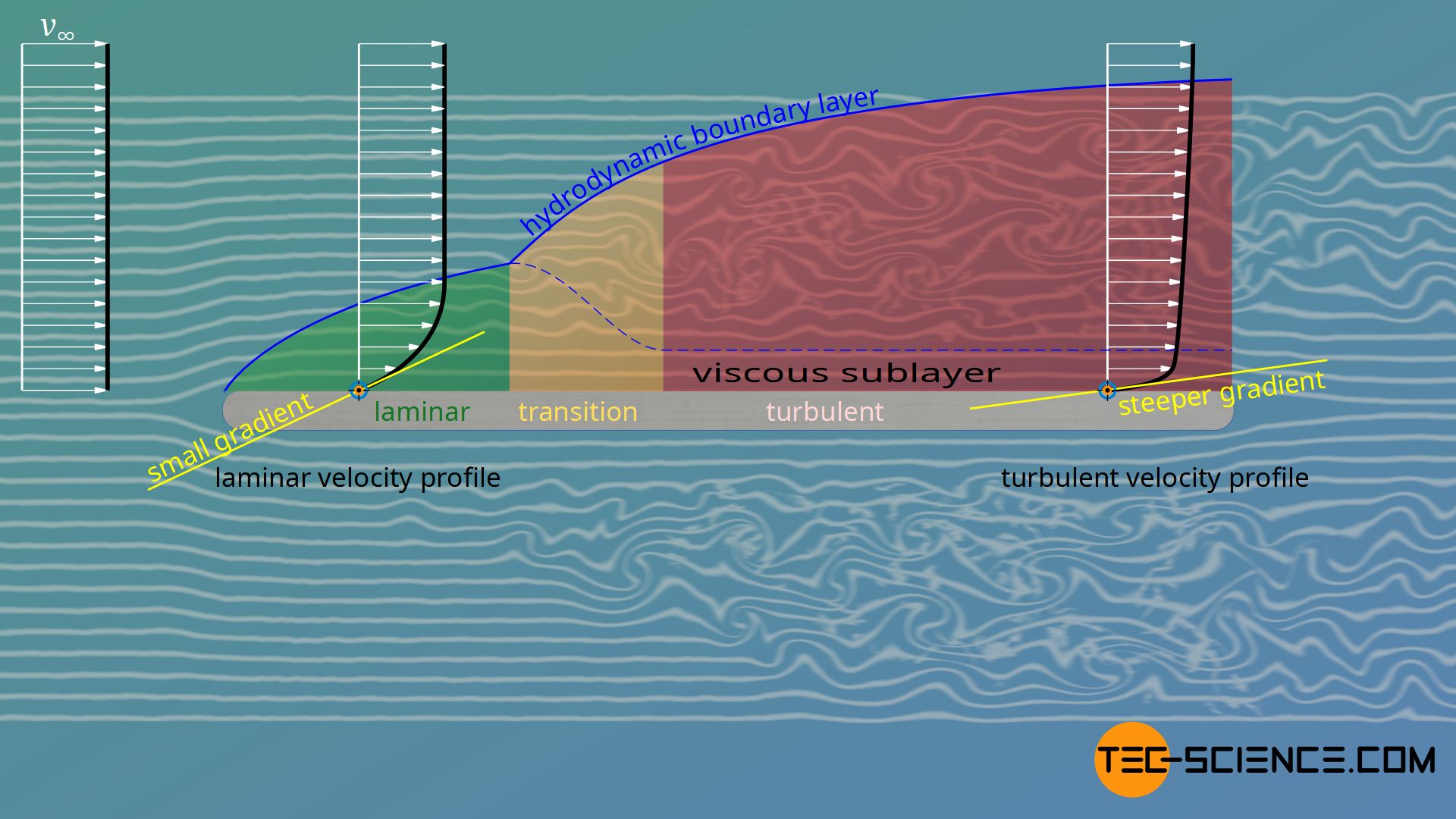
Due to the larger velocity gradients, higher wall shear stresses act in turbulent boundary layers. These higher shear stresses ultimately mean higher drag. Note that even with a turbulent boundary layer, a laminar sublayer forms directly on the wall (also called viscous layer). Newton’s law of fluid friction therefore remains valid even in the case of a turbulent boundary layer; at least directly on the wall.
Turbulent boundary layers have larger velocity gradients at the wall, which leads to a higher wall shear stress (higher friction drag) due to the viscous layer!
The increased drag caused by turbulent flows around cars, for example, are attempted to be prevented by avoiding turbulence as far as possible and therefore making the body as streamlined as possible.
Pressure drag (form drag)
In the case of streamlined bodies, almost the entire drag is due to the frictional force or the wall shear stress between the fluid and the wall. In fact, there is another phenomenon that influences the overall drag. For example, the pressure in the fluid in front of the plate is not necessarily the same as behind the plate. In general, there are pressure differences. How does this happen?
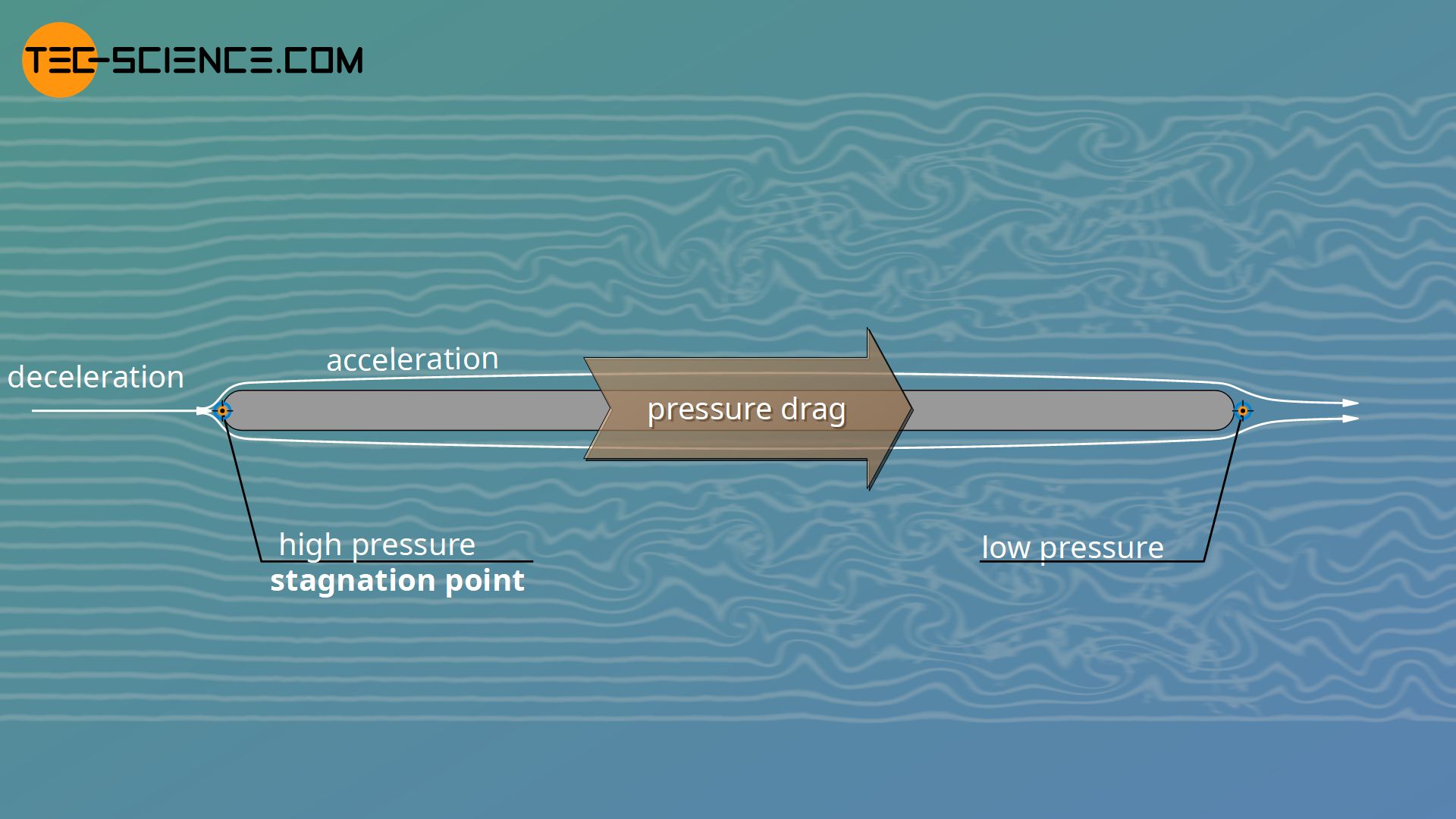
Let us consider the flow of the fluid around the plate. In front of the plate, the pressure is generally higher because the fluid is stagnated there. This is why one also speaks of a so-called stagnation point. A stagnation point is characterized by the fact that the fluid hits the surface perpendicularly and is theoretically slowed down to zero.
Due to the Brownian motion, the fluid molecules at the stagnation point does not really remain motionless in place. Rather, sooner or later the molecules will diffuse out of the stagnation point and be accelerated again by the surrounding fluid. Moreover, the stagnation point is a single point without expansion (singularity), while the fluid molecules have a certain size. The fluid particles can therefore not be located exactly at this point to actually be completely decelerated to zero.
Let’s look at the situation from an energy perspective. The kinetic energy of the fluid has been completely converted into pressure energy at the stagnation point (see also the article Bernoulli’s principle). More precisely: the dynamic pressure of the flow is converted into static pressure. The resulting pressure is also known as stagnation pressure.
The stagnation point is the point in a flow field at which the fluid flows perpendicular to an object and is theoretically decelerated to zero. The resulting static pressure is called stagnation pressure; it is a consequence of the conversion of kinetic energy into pressure energy.
After the fluid has been slowed down at the stagnation point by increasing the static pressure, it is then directed around the plate. In the process, it accelerates and pressure energy is now converted back into kinetic energy. As a result, static pressure decreases again, so that pressure behind the plate is lower than in front of the plate.
Thus, the greater static pressure in front of plate is tempted to push the plate backwards (in the direction of the flow). Besides the skin friction drag, this becomes noticeable as a further kind of drag. In this context one also speaks of pressure drag. The pressure drag is significantly influenced by the form of the body around which the flow passes, since the shape has an effect on the speed (kinetic energy) of the flow and thus determines the distribution of static pressure around the body.
The pressure drag (form drag) of a body around which a fluid flows is a consequence of the different static pressures caused by different speeds of the fluid.
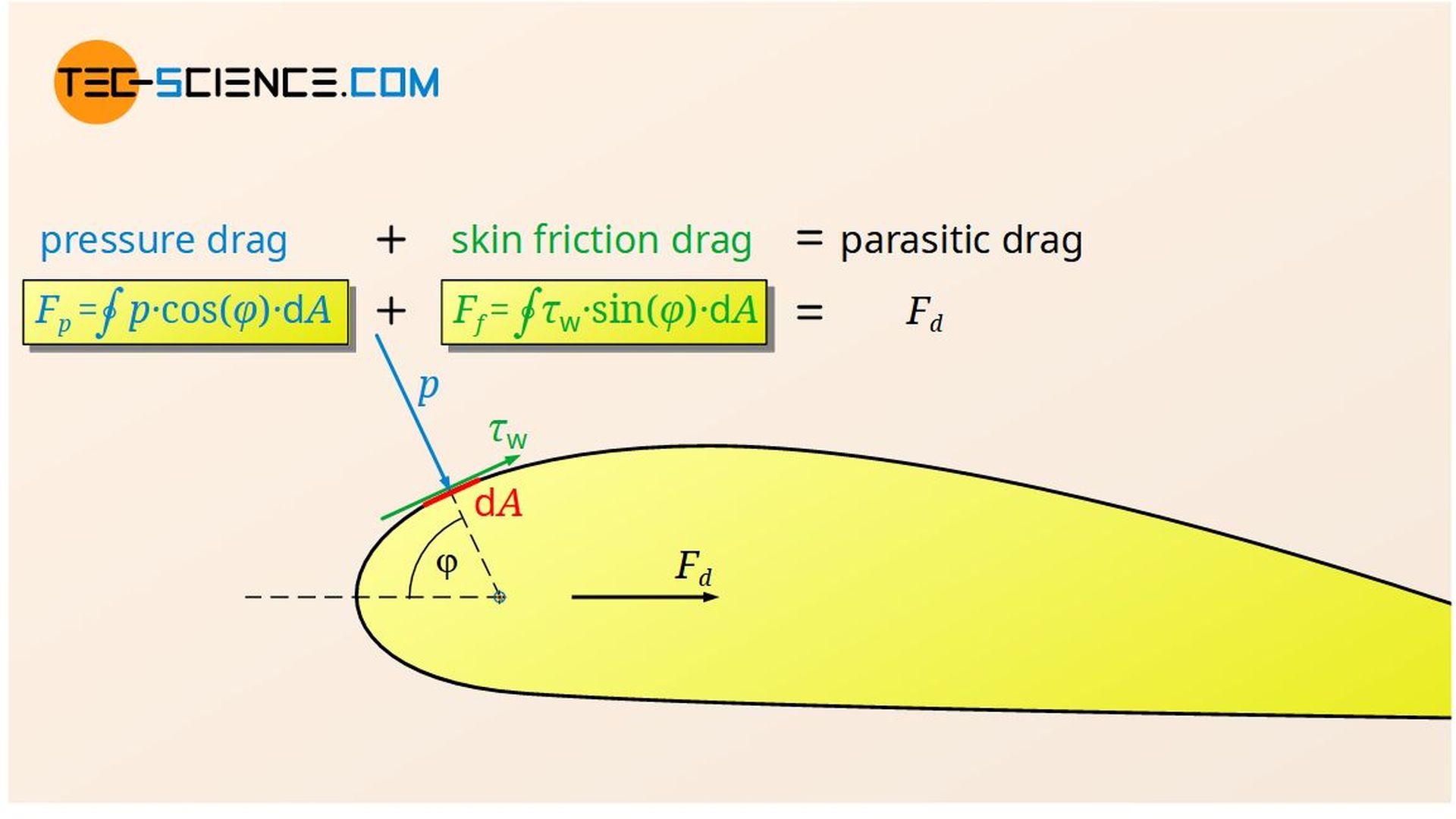
Note that the skin friction drag mentioned in the previous section is ultimately due to shear stresses (shear stress drag), while the pressure drag acts perpendicular to the surface and thus as normal stresses (normal stress drag). The force parallel to the surface is therefore decisive for the drag in the case of friction drag and the force perpendicular to the surface in the case of pressure drag.
For a analytical determination of the pressure drag for arbitrarily shaped bodies, the pressure distribution over the entire surface must be considered and no longer only the pressure in front of and behind the object. The same applies to the skin friction drag, for which the distribution of the velocity gradient over the entire surface must be considered.
Influence between external flow and boundary layer
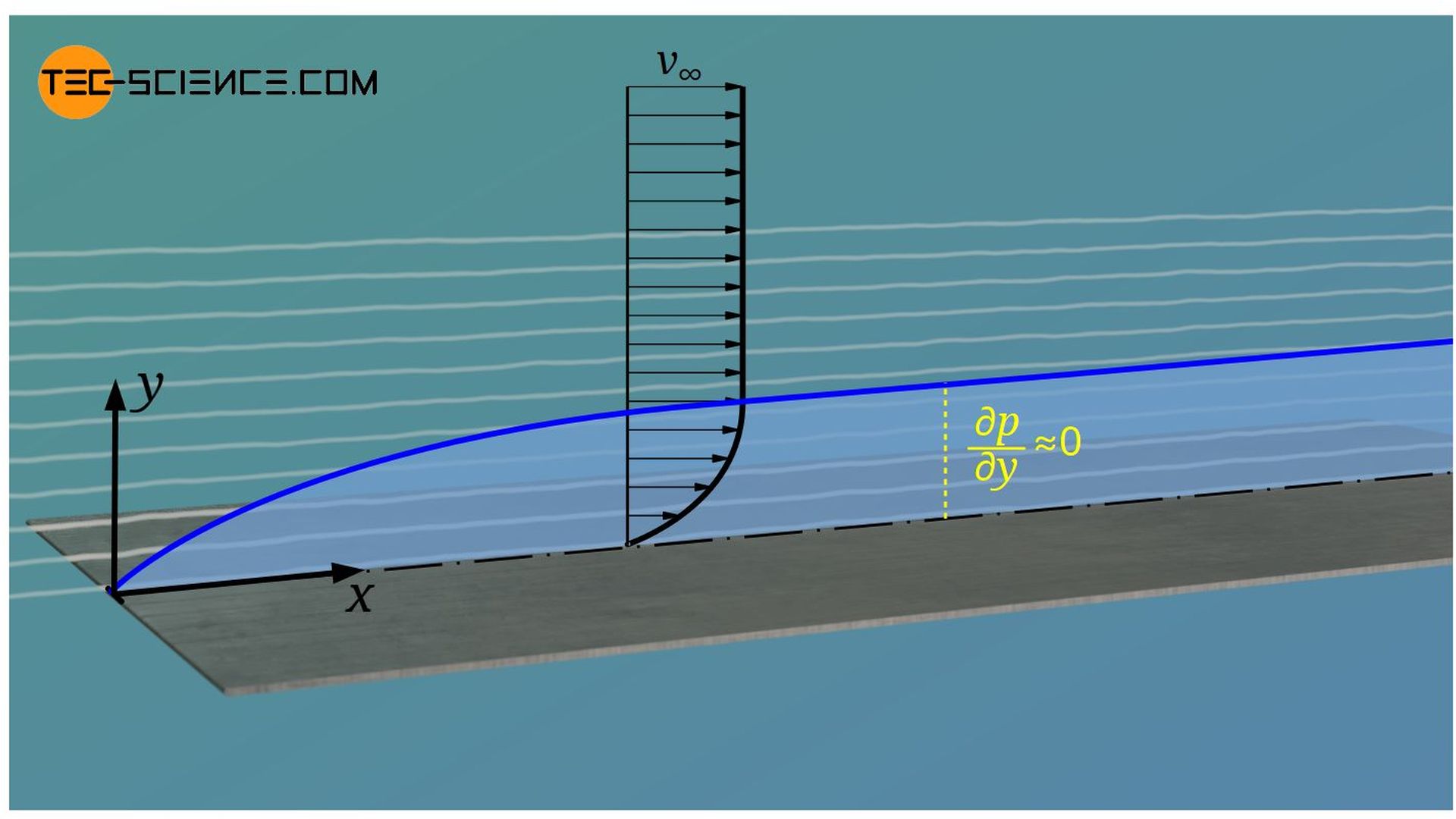
The pressure drag is determined by the static pressure acting on the surface of the body being flowed around. The undisturbed external flow imposes its static pressure on the boundary layer! In vertical direction to the plate the (static) pressure gradient is therefore close to zero (∂p/∂y=0), i.e. the pressure within the boundary layer hardly changes in y-direction. The boundary layer and the outer flow thus influence each other.
The flow within the boundary layer displaces the outer flow. Conversely, the outer flow imposes its (static) pressure on the boundary layer and thus influences its course!
Overall drag (parasitic drag)
Summary: A body that is flowed around by a fluid experiences a drag that has two causes. On the one hand, frictional forces act as a result of the viscosity and on the other hand, pressure forces act as a result of different flow speeds. Both types of drag, i.e. skin friction drag and pressure drag, finally form the so-called parasitic drag which is ultimately the overall drag. Sometimes the parasitic drag is also referred to as profile drag.
The parasitic drag (profile drag) of a body generally consists of the skin friction drag (“shear stress”) and the pressure drag (“normal stress”)!
In order to keep the overall drag as low as possible, it is therefore particularly important to prevent the fluid from stagnating on the body surface. This is achieved by a body shape that is as streamlined as possible. The overall drag is thus lower, and is mainly due to the friction drag.
The more streamlined a body is formed, the lower the influence of the pressure drag and the greater the influence of the skin friction drag!
Note that basically any form of energy dissipation results in a decrease in static pressure (Bernoulli’s principle). So as long as frictional forces are acting, pressure drag can never be avoided. This is particularly important in turbulent flows that occur immediately behind an obstacle. Such turbulences mean a high energy dissipation and thus a strong reduction of static pressure. The pressure drag increases strongly in these cases.
As is usual in fluid mechanics, dimensionless similarity parameters are introduced to describe the different types of drag independently of the size of the system. In this way it is possible to draw conclusions about the real system, for example by using scaled-down models in wind tunnel. These dimensionless numbers are called drag coefficients. This is discussed in more detail in the linked article.