Definition of the specific heat capacity
The specific heat capacity c describes the relationship between a transfer of heat Q and the associated temperature change ΔT of a substance of mass m:
\begin{align}
\label{q}
& \boxed{Q = c \cdot m \cdot \Delta T} \\[5px]
\end{align}
In the article Specific heat capacity (derivation and definition), the derivation of this formula is shown using the example of the heating of water. In the following, important limitations of this formula are explained in more detail.

Heat loss
When experimentally determining the specific heat capacity of water by heating it with an immersion heater, a larger value is generally determined than the substance actually has.

The reason for this is that the heat given off by the immersion heater is not completely transferred to the water. Part of this heat is also used to heat the vessel and the surroundings. This means that the water only benefits from less heat energy than theoretically calculated on the basis of the electrical output of the immersion heater. More information on this and a way to avoid this systematic error can be found in the article Calorimeter to determine the specific heat capacities of liquids.
Heating vs. cooling
As already noted, formula (\ref{q}) was derived on the basis of a heating process. However, due to the conservation of energy, this relationship between heat transfer and temperature change also applies to a cooling process, where the temperature is to be decreased by a certain amount ΔT. In this case, the amount of heat Q, which is also determined according to formula (\ref{q}), must be transferred by the substance to the surroundings (released by the substance, so to speak).

Since the temperature change is negative when a substance is cooled, there is also a negative sign for the amount of heat to be released. The sign of the heat thus indicates whether heat is transferred from the surroundings to the substance (heating) or heat is transferred from the substance to the surroundings (cooling). A positive value means that heat must be supplied to the substance. If the heat has a negative sign, the amount of heat must be released from the substance.
The specific heat capacity describes the relationship between heat and temperature change not only for a heating, but also for a cooling!
Limitation of validity in the case of phase transitions
Formula (\ref{q}) is only valid as long as the state of matter of a substance does not change, e.g. no phase transition takes place. At phase transitions the relationship between heat and temperature change is no longer valid in this form! This already shows the everyday experience with the boiling of water. During vaporization, the temperature of the water remains constant at 100 °C despite further heat input, until at some point all the water has vaporized. Obviously, for phase transitions formula (\ref{q}) is no longer valid!

The specific heat capacity is only valid as long as no phase transition takes place!
Of course, heat must also be transferred to or by a substance during a phase transition in order to drive the process. The calculation of such latent heats is described in more detail in the article Specific heat of vaporization (latent heat).
Dependence of the specific heat capacity on the state of matter and on the temperature
The specific heat capacity is actually not constant for a substance, but depends decisively on the state of matter. For example, the specific heat capacity of water drops by around half when water is no longer liquid but gaseous. Gaseous water is present, for example, in the pipelines of steam driven power plants, where the water is heated to over 500 °C.
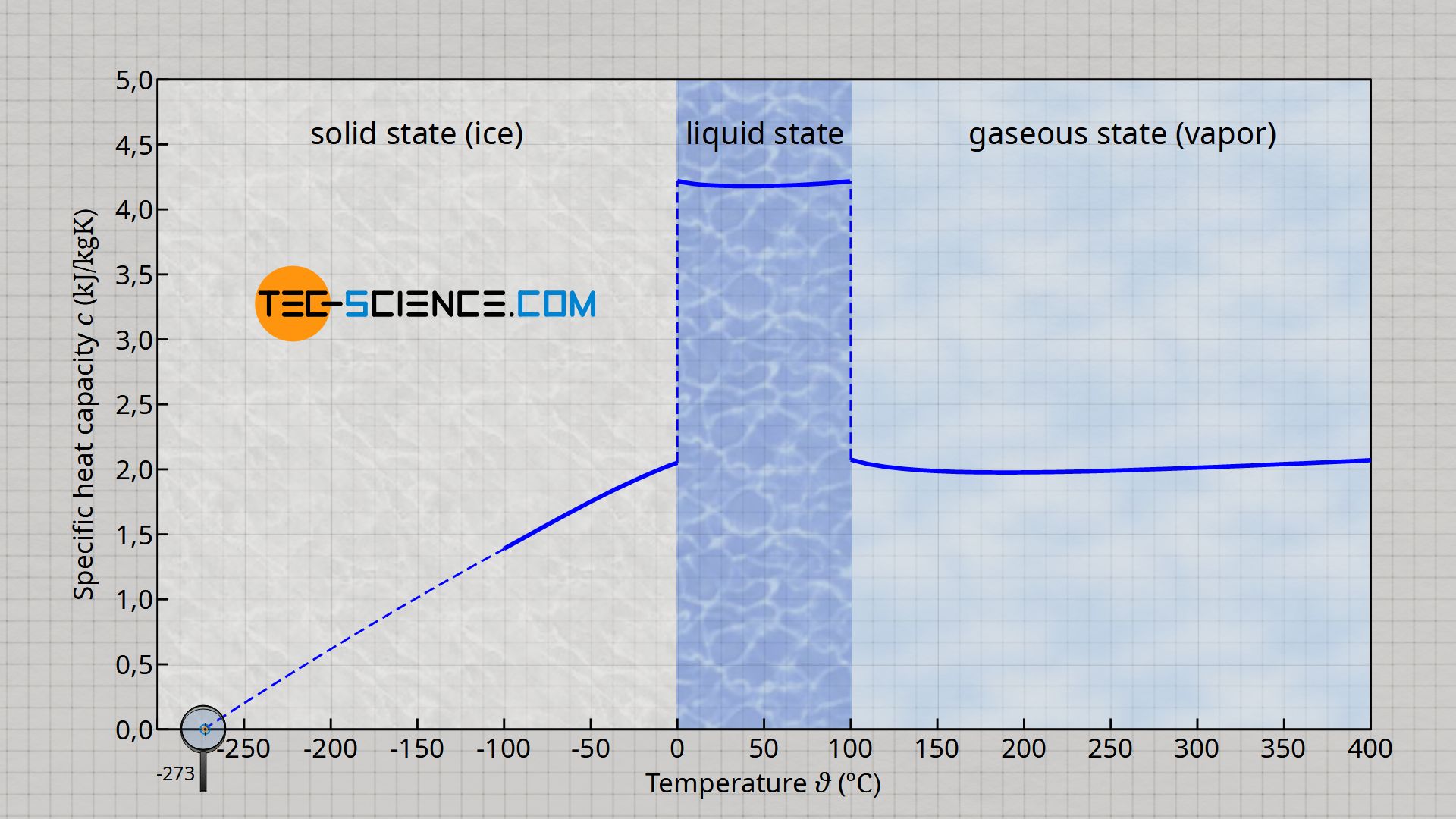
Furthermore, the specific heat capacity can depend to a greater or lesser extent on the temperature. In the case of water, such a temperature dependency is especially given in the solid state (ice). Up to absolute zero, the specific heat capacity of ice decreases continuously. More information on this can be found in the article Specific heat capacity of water.
Dependence of the specific heat capacity on the process of heat transfer
When heating or cooling a substance, a distinction must generally be made between whether heat is transferred at constant pressure (isobaric process) or at constant volume (isochoric process). Depending on the process, the specific heat capacity and thus the temperature change caused by a certain amount of heat differs.
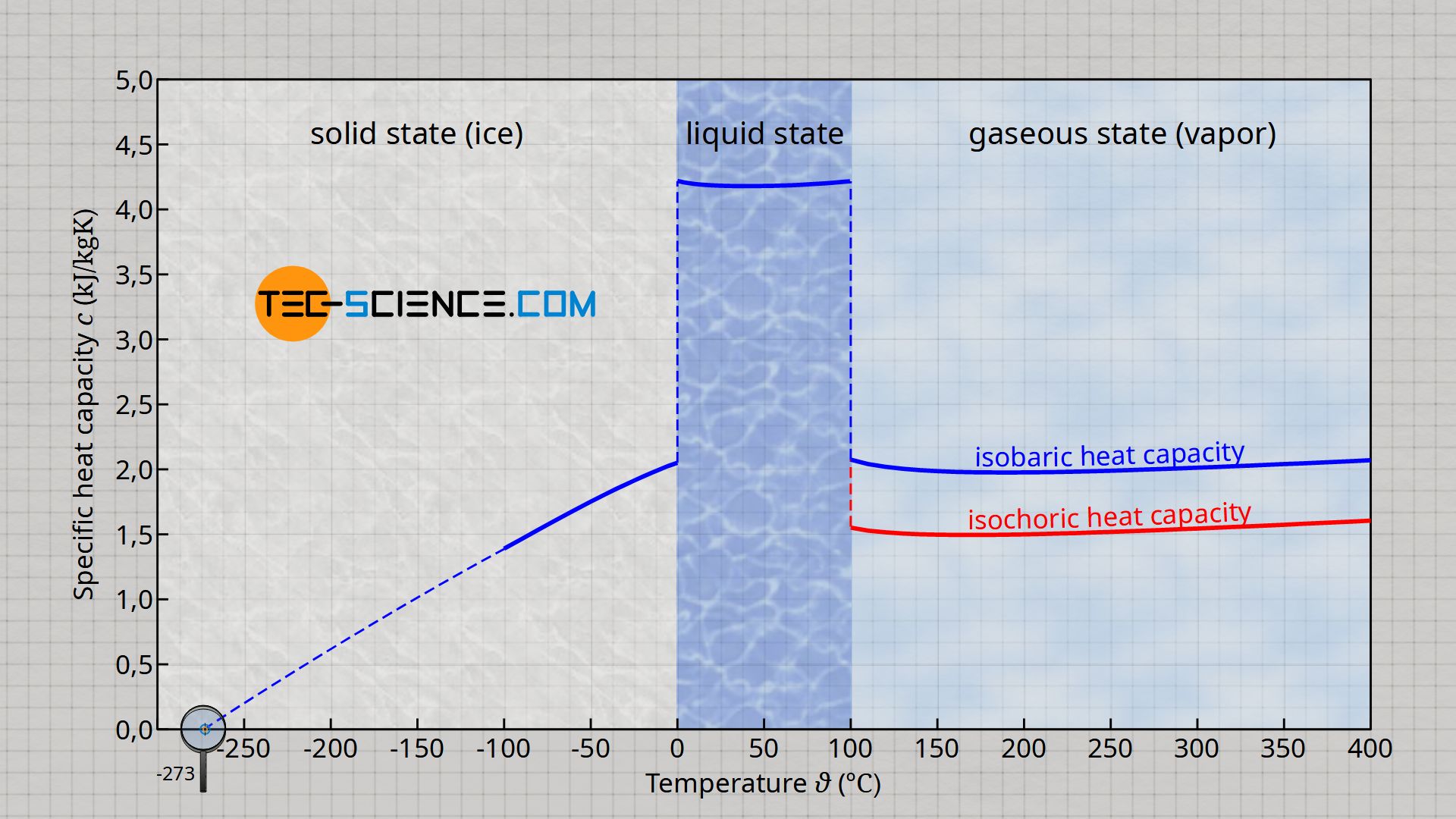
With an isobaric process, more heat must be transferred for the same temperature increase, since the heat is not completely used for the increase in temperature (increase of the internal energy), but a part is converted into work required for the expansion of the substance. With an isochoric process, on the other hand, the heat can be used completely to increase the temperature. Thus, the same temperature change already occurs with a less amount of heat.
For this reason, a distinction is made between the specific heat capacity of an isochoric process cv and the specific heat capacity of an isobaric process cp, where cp>cv. This distinction must be made especially for compressible substances such as gases, which change their volume very strongly with temperature. For more information, see the article Specific heat capacity of gases (at constant volume or pressure).
In the case of incompressible substances such as solids and liquids, such a distinction between isobaric and isochoric heat transfer does not usually have to be made. On the one hand, these substances change their volume only slightly when heated or cooled, so that the two values often hardly differ from each other. On the other hand, heat transfer for these substances usually takes place under the condition that they can expand freely. Thus, the heat is transferred usually at constant ambient pressure and thus corresponds to an isobaric process. In the case of liquids and solids, therefore, only the specific heat capacity of the isobaric process is usually relevant anyway, which is then simply denoted by c.
Misleading terminology of “capacity”
In connection with the specific heat capacity, the term capacity is intended to describe the ability of a substance to absorb heat without any noticeable change in temperature. In other words, a very high heat absorption capacity without a significant change in temperature.
The term capacity is in this respect somewhat misleadingly chosen, because in thermodynamics heat is not considered a state quantity, but a process quantity. There is no capacity of a substance in the sense of a storage of heat! The absorbed heat is stored at an atomic level as internal energy!
Calorie
The quantity calorie, which is still in use in connection with the energy content of food, has its origin in the heating of water. The amount of heat required to raise the temperature of 1 g of water by 1 °C was defined as 1 calorie (cal). Thus, 1 cal corresponds to an amount of heat energy of 4.2 J.
One calorie corresponds to the amount of heat that heats water of mass 1 g by 1 °C (1 cal ≙ 4.2 J)!
The more commonly used unit in food industry is the kilocalorie (kcal), which corresponds to an energy value of 4.2 kJ (also referred to as food calorie or Calorie with C as a capital letter!).






