Due to compressibility of gases, a distinction must be made between the isobaric and the isochoric specific heat capacity.
Differentiation between isochoric and isobaric heat transfer
Unlike liquids or solids, gases are special when it comes to the specific heat capacity. For these substances, the way in which the heat is transferred must be taken into account. Two cases must be distinguished, which will be demonstrated by an experiment in the following:
- heat transfer at constant volume (isochoric process)
- heat transfer at constant pressure (isobaric process)
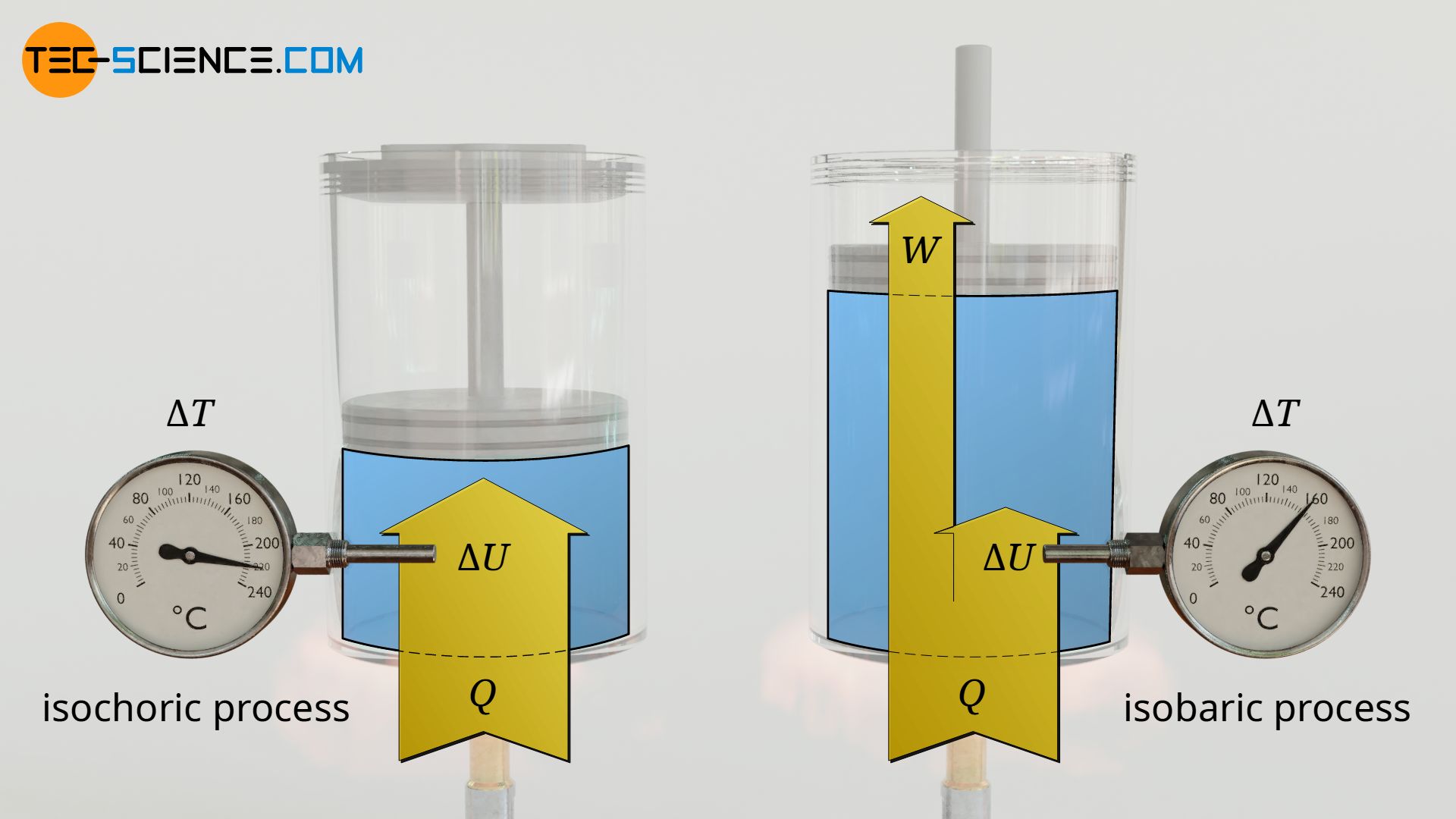
Experimental setup
In the first case, the confined gas volume is kept constant during heating. This is done by locking the piston in the cylinder. This causes the gas pressure in the cylinder to increase during heating (as is the case, for example, with pressure cookers). Such a thermodynamic process in which the volume remains constant is called an isochoric process.

A process in which the volume of a confined gas does not change is called an isochoric process!
In the second case, the gas pressure is kept constant during heating. This is achieved by allowing the pistons to move freely in the cylinder this time. This allows the gas to “yield” to the otherwise increasing pressure by increasing its volume so that the pressure remains constant (as is approximately the case, for example, in diesel engines during combustion of fuel). A thermodynamic process in which the pressure remains constant is called an isobaric process!
A process in which the pressure of a confined gas does not change is called an isobaric process!
Observation
The reason why these two processes have to be distinguished in the case of gases can be seen if the gas is heated and the temperature increase is observed in each case. For this purpose, in both cases the gas is heated with a Bunsen burner for the same period of time. Thus, it can be assumed that the same amount of heat was absorbed by the gas.
However, it can be seen that the temperature increase is significantly greater for the isochoric process than for the isobaric process. Another difference in the observation of the two experiments is that in the isobaric process, the gas volume expands due to the heating and thus pushes the piston upwards.
Evaluation
What is the reason for the different temperature change in the two cases?
While with the isobaric process work was obviously done by the gas to push the piston upwards against its weight (and against the ambient pressure!), no work was done by or on the gas with the isochoric process. Thus, in the isobaric process, the transferred heat energy is not fully used to increase the kinetic energy of the gas molecules (= increase in temperature!). Part of the transferred heat energy is converted into work and is thus not available for increasing the temperature. That part of the heat energy which leads to the increase of the kinetic energy of the molecules and thus to the increase in temperature benefits the so-called internal energy ΔU.
The temperature increase is therefore lower for an isobaric heating, although the same amount of heat was absorbed by the gas. The relationship between transferred heat and the temperature change are therefore different for the isochoric process and the isobaric process. This leads to the fact that the specific heat capacities for gases are different depending on the thermodynamic process (heat is therefore a so-called process quantity).
Note: Since the gas volume obviously has to change during the isobaric process in order to keep the pressure constant, the work done by the gas (or the work done on the gas in the case of compression/cooling) is also referred to as pressure-volume work. Note that the gas would have to do work even if the piston was weightless. In this case, the gas would only have to expand against the surrounding air pressure (1 bar), but even this requires work.
Conclusion
As has been shown, with isobaric heating the same amount of heat thus leads to a smaller temperature change than with isochoric heating. Conversely, this means: To obtain the same change in temperature, more heat must be supplied during isobaric heating to compensate for the work done in the process. Consequently, the specific heat capacity is always larger in the isobaric case compared to the isochoric process!
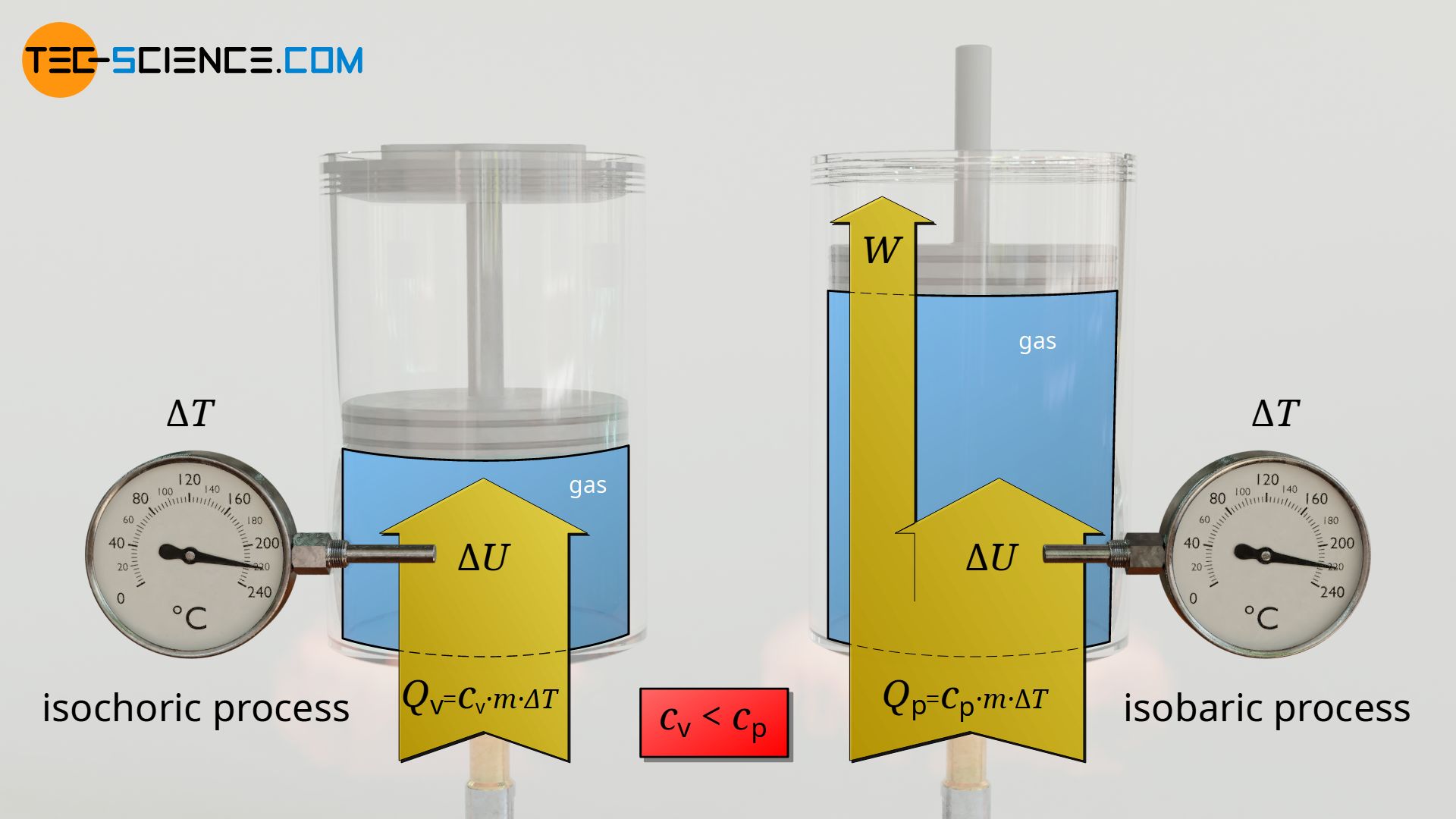
The specific heat capacity at constant pressure (isobaric process) is always larger compared to the specific heat capacity at constant volume (isochoric process), because work has to be done!
For the purpose of distinction, the specific heat capacity at constant pressure is therefore denoted by cp and at constant volume by cv. For air, for example, cp is 1.005 kJ/(kg⋅K) and cv equals 0.718 kJ/(kg⋅K).
\begin{align}
& \boxed{Q_\text{v} = c_\text{v} \cdot m \cdot \Delta T} ~ \text{isochoric process} \\[5px]
& \boxed{Q_\text{p} = c_\text{p} \cdot m \cdot \Delta T} ~ \text{isobaric process} \\[5px]
& \boxed{c_\text{p} > c_\text{v}} \\[5px]
\end{align}
More detailed investigations show that the specific isobaric heat capacity cp is larger than the specific isochoric heat capacity cv by the amount of the specific gas constant Rs.
\begin{align}
&\boxed{c_\text{p} = c_\text{v} + R_\text{s}}
\end{align}
Differentiation for incompressible substances such as liquids and solids
Note that the distinction between cp and cv is only relevant for substances which are in principle able to do pressure-volume work. In practice, this only applies to compressible substances such as gases, as these can change their volume very strongly under pressure. For solids and liquids such a distinction is obsolete, since they are incompressible in contrast to gases. Such substances can practically not change their volume under pressure and consequently cannot do any kind of pressure-volume work. The low thermal expansion is negligible. Therefore, the specific heat capacity for solids and gases is only denoted by the symbol c (without any index).






