The specific heat capacity indicates how much heat must be absorbed by a substance of mass 1 kg in order to increase its temperature by 1 K (1 °C).
Introduction
The temperature of a substance can be increased by absorbing heat or by releasing heat. The extent to which the temperature changes depends on the kind of substance. Compared to many other substances, water, for example, reacts to a heat input only with a relatively small temperature increase.This also applies to cooling: when heat is released, the temperature of water decreases very little compared to many other substances.
Such a “slow” behavior of water to react to a heat transfer is very clearly shown in the climate of some regions. In regions that are located near large amounts of water, temperature fluctuations over the course of the year are significantly smaller than in regions without large amounts of water in the vicinity. Water masses obviously change their temperature much less compared to land masses when they are heated in summer or cooled in winter (see climograph of Aberdeen and Green Bay in the figure below).
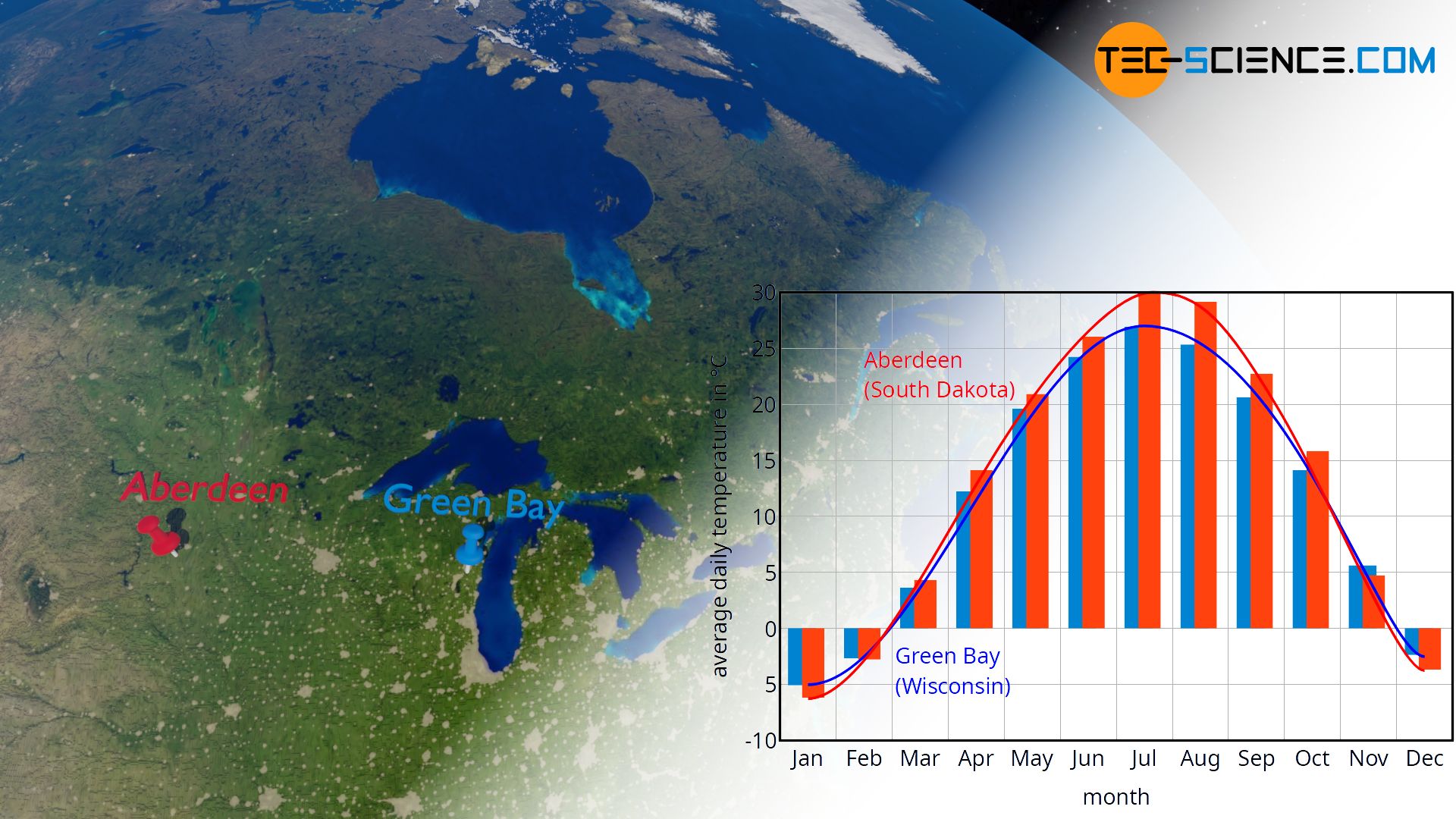
The question arises how to calculate the temperature change for a given amount of heat to be absorbed or released for the different substances. Or, to put it the other way round: what amount of heat must be transferred in order to achieve a certain change in temperature?
Influencing quantities
For a given substance, two quantities determine the amount of heat to be transferred to cause a desired temperature change. One is the temperature change itself. It can be assumed that the greater the desired temperature change, the more heat must be transferred. This is already evident from everyday experience when heating water on a hotplate. The more the water is to be heated, the more heat must be transferred, i.e. the longer the water must stay on the hotplate.

Another influencing factor is the mass of the substance to be heated. It can be assumed that the greater the mass to be heated, the more heat must be absorbed by the substance. This is also shown by everyday experience when heating water on a hotplate. Heating a large amount of water takes much longer than heating a smaller amount of water, i.e. for large amounts of water, more heat must be transferred to achieve the same temperature change as for a small amount.
Experimental setup
In order to systematically investigate the above-mentioned parameters influencing the amount of heat, water is used as an example in the following. For this purpose, a certain mass of water is heated with an immersion heater and the temperature change is measured over time. The experiment is then repeated with different masses of water.

The overall heat transferred up to a certain point in time is determined by the electrical power of the immersion heater. The electrical power is completely converted into heat and thus equals the rate of heat flow (= “heat energy per unit time”). If the electrical power of the immersion heater is 500 W, for example, 500 J of heat energy is supplied to the water each second, neglecting heat losses. Thus, from the electrical power P, one can determine the amount of heat Qt transferred up to the time t using the following formula:
\begin{align}
\label{q}
& Q_\text{t} = P \cdot t \\[5px]
\end{align}

The temperature change measured during the experiment as a function of time can then be converted into a dependence on the transferred heat using this formula (temperature change as a function of heat).
Evaluation
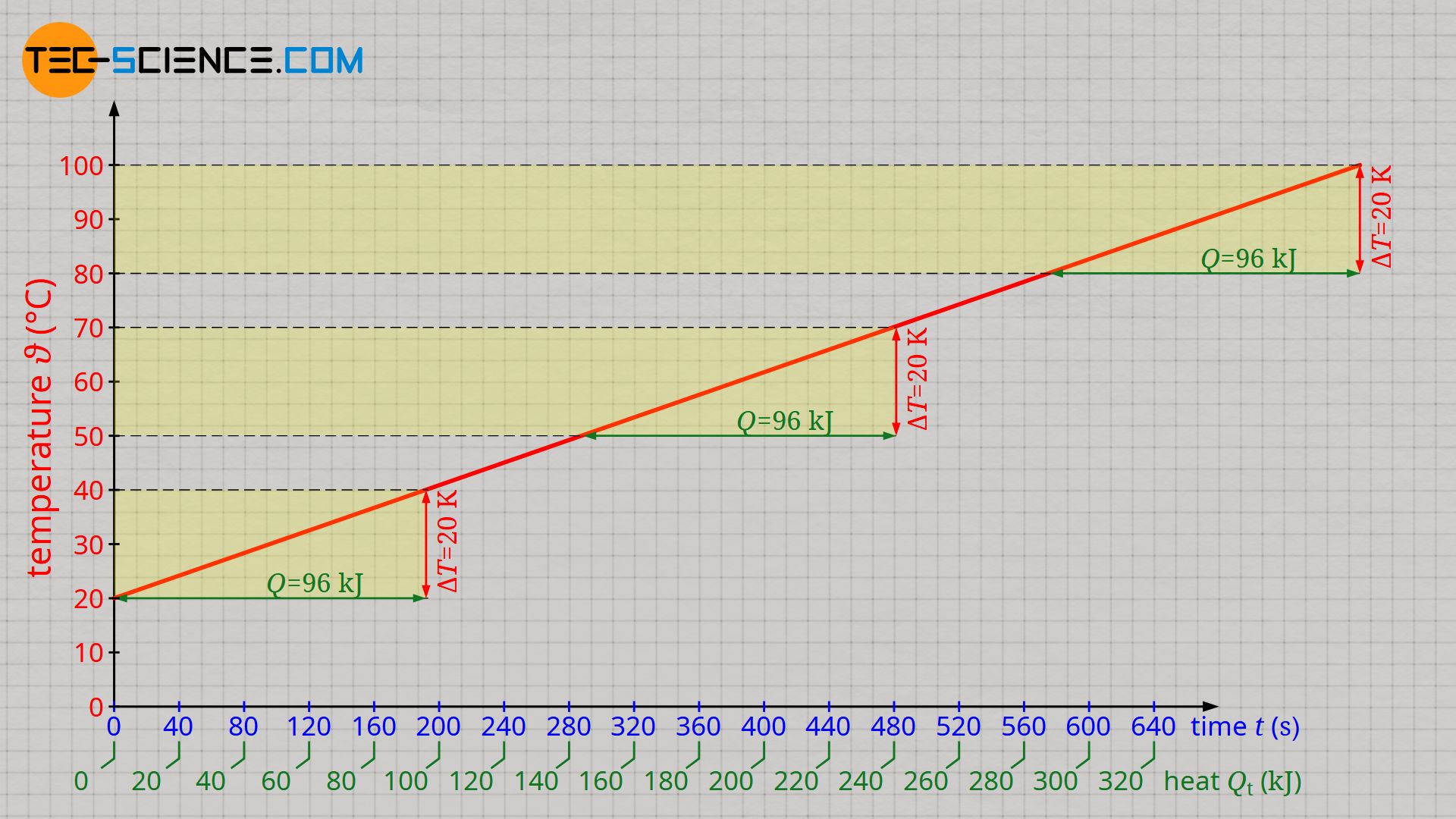
The figure below shows the evaluation of the experiment with an immersion heater of 500 W power. The values on the horizontal axis on which the time is plotted were also converted into a amount of heat according to formula (\ref{q}). In principle, there is a linear relationship between the heat transferred and the increase in temperature.
Due to the constant increase in temperature it becomes clear that the transfer of a certain amount of heat Q always leads to the same temperature change ΔT. This is independent of the temperature. Thus, for a temperature increase from 20 °C to 40 °C, the same heat of 96 kJ has to be transferred as for the temperature increase from 50 °C to 70 °C. The same amount of heat of 96 kJ must also be transferred for heating from 80 °C to 100 °C. So the temperature itself has (almost) no influence on the amount of heat that has to be absorbed by the water to cause a certain temperature change!
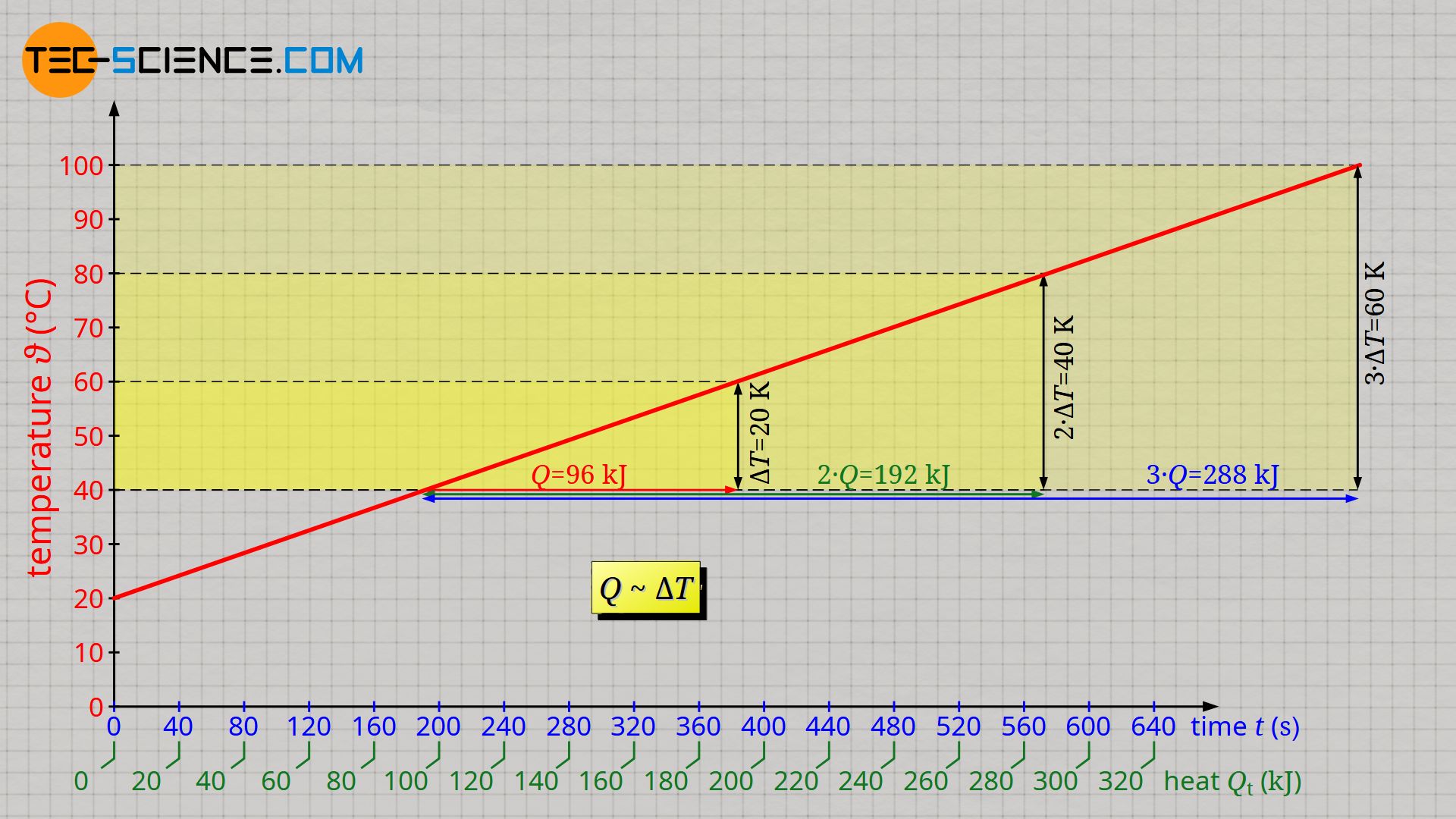
The linear increase in temperature also shows that twice the change in temperature requires twice the heat. Should the temperature change be three times as great, three times as much heat will be required. Heat Q and temperature change ΔT are therefore proportional to each other:
\begin{align}
& Q \sim \Delta T \\[5px]
\end{align}
Note: Q in the above formula does not denote the total heat transferred up to a certain point in time, but only the heat transferred that causes the temperature change ΔT!
If the experiment is carried out with half the amount of water, it is observed that the temperature rises twice as much within a certain time. If, on the other hand, twice the amount of water is heated, the temperature rises only half as much. Or to put it the other way round: If the same temperature change is to be achieved in both cases, then only half the heat must be transferred with half the water mass and twice the heat with twice the water mass.
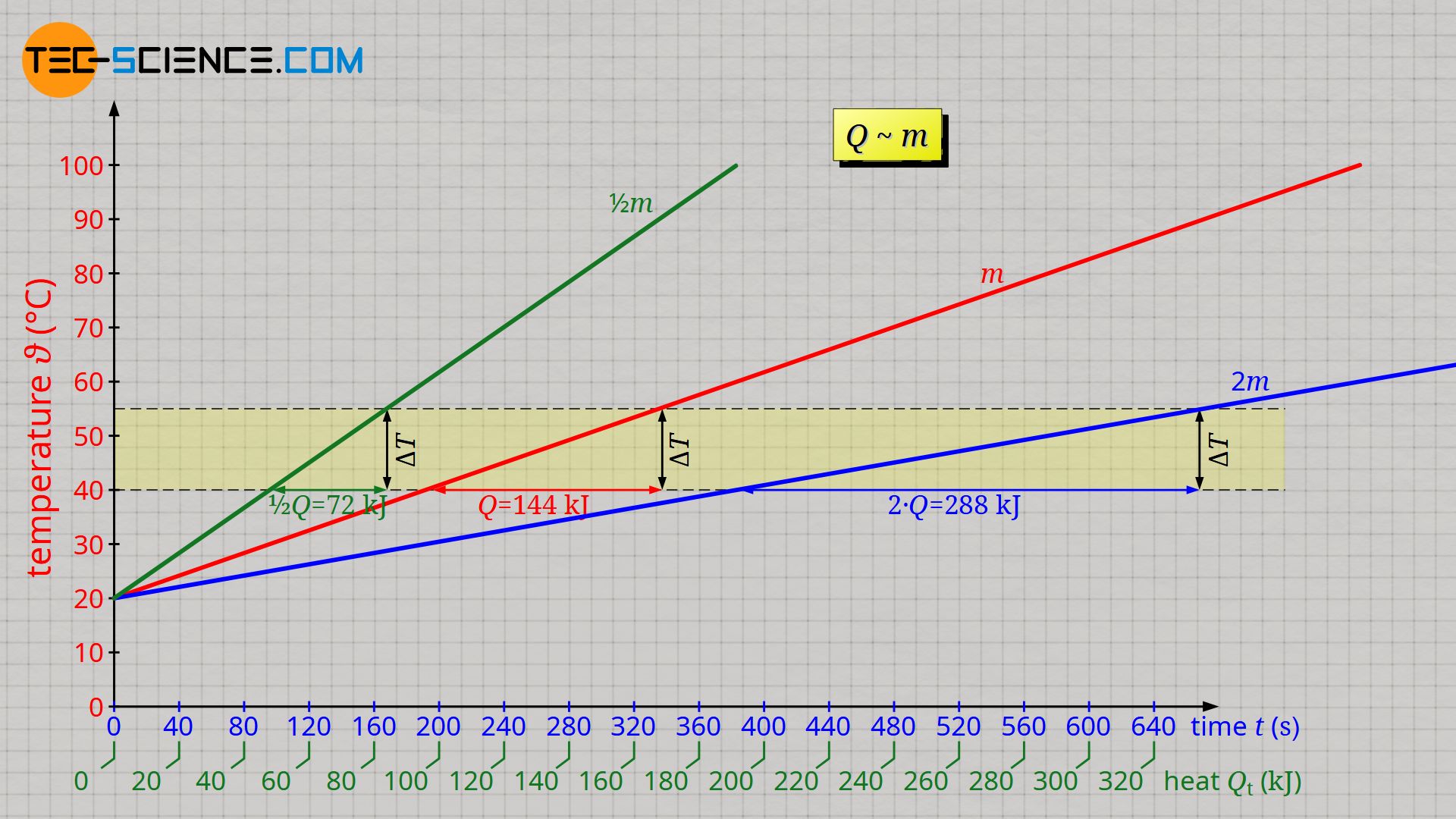
This becomes vividly clear. Just imagine that you would divide the doubled water mass into two smaller water masses of the original mass and then heat them both simultaneously with two immersion heaters. The two immersion heaters would therefore transfer twice the amount of heat in total.

Thus, the amount of heat that must be transferred to cause a given temperature change and the mass of water to be heated are proportional to each other:
\begin{align}
& Q \sim m \\[5px]
\end{align}
Conclusion
The evaluation of the experiment thus shows that the quantity of heat Q is both proportional to the desired temperature change ΔT and proportional to the mass m to be heated. So overall, the amount of heat Q is proportional to the product of temperature change ΔT and mass m:
\begin{align}
& Q \sim m \cdot \Delta T \\[5px]
\end{align}
Thus, the quotient of heat Q and the product of mass m and temperature change ΔT is constant and can be defined as a proportionality constant. This proportionality constant is called specific heat capacity c and is a material property of the substance to be heated. For water, the specific heat capacity in the present experiment is determined to be 4.8 kJ/(kg⋅K) (literature value: 4.2 kJ/(kg⋅K)). To find out why the experimentally determined value is larger than the literature value and how this systematic error can be corrected, see the article Calorimeter for determining the specific heat capacities of liquids.
\begin{align}
& \boxed{\frac{Q}{m \cdot \Delta T} = \text{constant} = c} ~~~~[c] = \frac{\text{kJ}}{\text{kg K}} ~~~ \text{specific heat capacity} \\[5px]
\end{align}
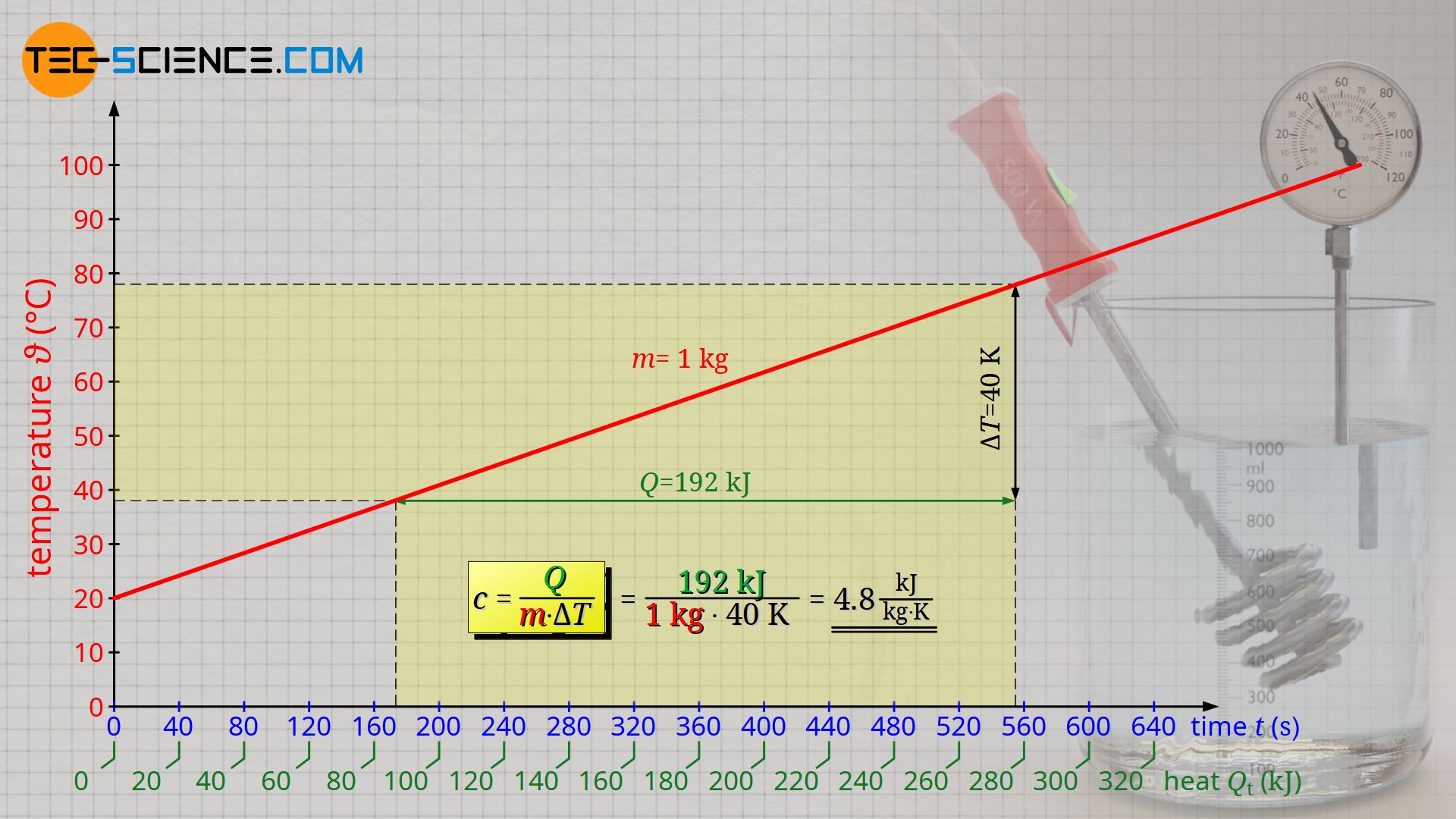
Note that the physically correct notation of a temperature change is not in the unit degrees Celsius (°C), but in the unit Kelvin (K). However, this has no influence on the numerical value of the temperature change, since the numerical value of a temperature change in Kelvin is the same as for degrees Celsius. Consequently, the specific heat capacity has the unit kJ/(kg⋅K).
Thus, as a material-dependent quantity, the specific heat capacity c describes the relationship sought between the transferred heat Q and the resulting temperature change ΔT for a given mass m:
\begin{align}
& \boxed{Q = c \cdot m \cdot \Delta T} \\[5px]
\end{align}
The specific heat capacity of substances can not only be understood as a mere proportionality constant, but can also be interpreted very clearly. A specific heat capacity of e.g. 4.2 kJ/(kg⋅K) (spoken: “four point two kilojoules per kilogram and kelvin”) means that for a mass of water of 1 kilogram, a quantity of heat of 4.2 kJ is required to heat the water by 1 °C (1 K).
The specific heat capacity of a substance indicates how much heat is required to change the temperature of mass 1 kilogram by 1 Kelvin (1 °C)!
In the article Specific heat capacity of selected substances, the specific heat capacity is explained in more detail with regard to the different behavior of substances when heated or cooled. Due to the complexity of this topic, further Important remarks on the specific heat capacity are discussed in more detail in the linked article.






