In this article, learn more about the specific heat capacity of different materials and how it affects the change in temperature over time during a heat transfer.
Definition of the specific heat capacity
The specific heat capacity indicates how much heat is required to increase the temperature a substance of mass 1 kg by 1 K (1 °C). The greater the specific heat capacity c of a substance, the more heat Q is required to cause a certain temperature change ΔT (assuming the same mass m:
\begin{align}
\label{q}
& \boxed{Q = c \cdot m \cdot \Delta T} ~~~~[c] = \frac{\text{kJ}}{\text{kg}\cdot \text{K}} \\[5px]
\end{align}

The specific heat capacity describes not only the relationship between heat input and temperature increase when a substance is heated, but also for the case when a substance is cooled. In this case, the specific heat capacity provides the relationship between a release of heat and the resulting temperature decrease.
Temperatur increase over time during heating
Substances with high heat capacities do not change their temperature as much as substances with low heat capacities when heat is transferred. This is directly evident when solving equation (\ref{q}) for the temperature change:
\begin{align}
& \boxed{\Delta T = \frac{Q}{c \cdot m}} \\[5px]
\end{align}
If heat is transferred to a substance not just once, but continuously, then the temperature will also increase permanently (provided there is no change in the state of matter). How fast the temperature rises depends on the specific heat capacity. For substances with low heat capacities, the temperature rises relatively quickly because relatively little heat is required to achieve a certain temperature change. In contrast, for substances with large heat capacities, the temperature increases only relatively slowly, since more heat is required until a certain temperature change occurs.
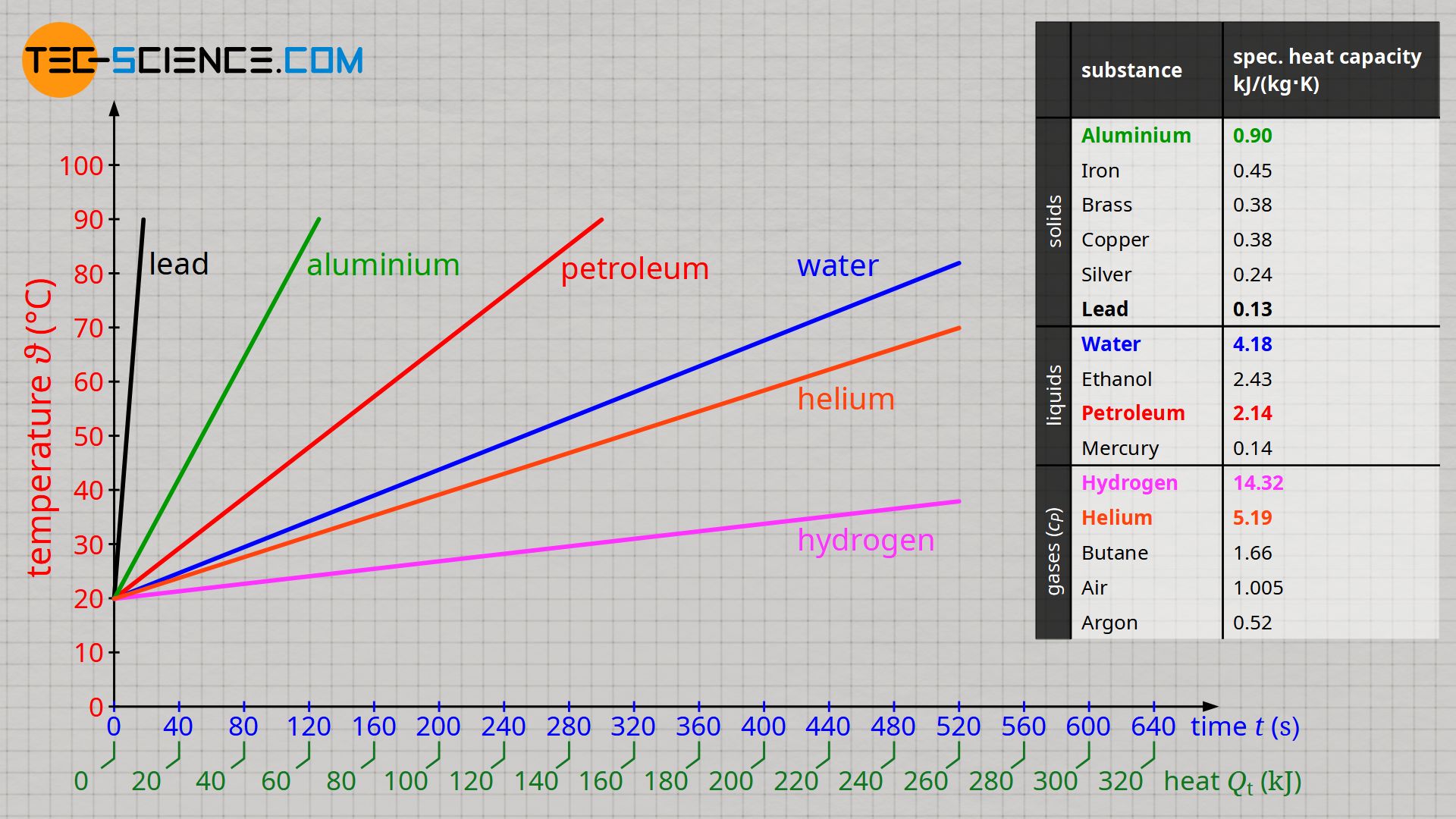
The figure above shows the heating curves of selected substances, each with a mass of 1 kilogram, at a heat input of 500 joules per second (= heating power 500 W). If a temperature-independent specific heat capacity can be assumed, the temperature curves are straight lines.
The higher the specific heat capacity of a substance, the flatter the temperature curve when heated with constant heat input (assuming the same mass)!
Specific heat capacity of selected substances
The table below shows the specific heat capacities of selected substances.
| Substance | Specific heat capacity c [kJ/(kg⋅K)] at 20 °C |
|---|---|
| Solids | |
| Aluminium | 0.90 |
| Iron | 0.45 |
| Brass | 0.38 |
| Copper | 0.38 |
| Silver | 0.24 |
| Lead | 0.13 |
| Liquids | |
| Water | 4.18 |
| Ethanol | 2.43 |
| Petroleum | 2.14 |
| Mercury | 0.14 |
| Gases cp (cv) | |
| Hydrogen | 14.3 (10.1) |
| Helium | 5.19 (3.11) |
| Butane | 1.66 (1.52) |
| Air | 1.01 (0.72) |
| Argon | 0.52 (0.31) |
When looking at the table above, the large specific heat capacity of hydrogen of 14.3 kJ/(kg⋅K) is particularly striking. Because of this high value, hydrogen is also used for cooling because it changes its temperature only to a small extent when heated by the material to be cooled – so it stays cold for a very long time! Helium also has such a property. In this context, a substance used for cooling is also generally referred to as a cryogen.
Although the gaseous substances helium and hydrogen have a higher specific heat capacity compared to water, it should be kept in mind that under normal conditions (and assuming the same mass), they occupy a much larger space! The figure below shows to scale the volumes of the different substances under normal conditions, i.e. at a pressure of 1 bar and a temperature of 0 °C.
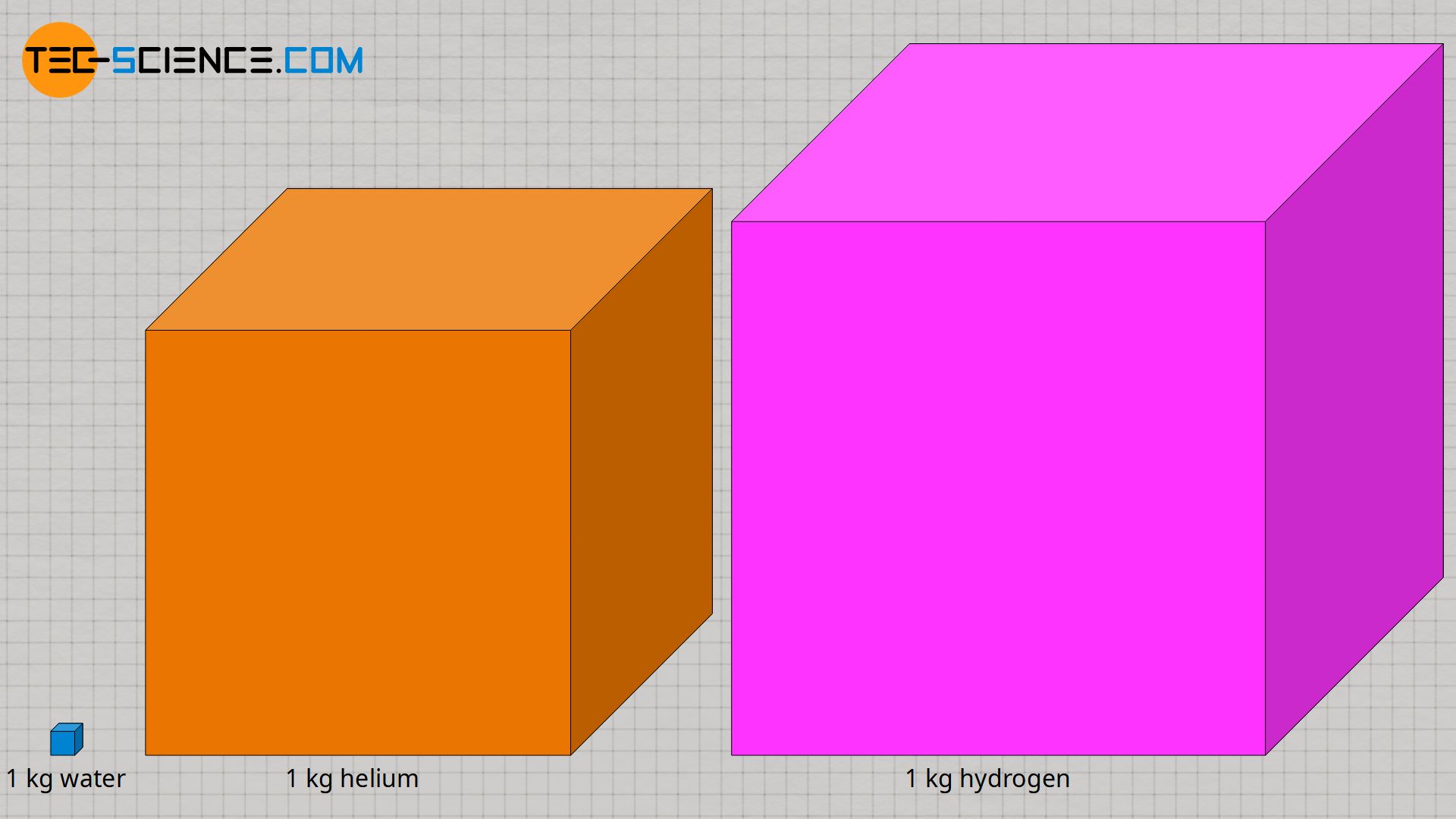
After helium and hydrogen, water has the largest specific heat capacity of all common substances and is particularly suitable for cooling or heating purposes in everyday life and in technology due to its high availability, manageability and small volume! More information, especially about the specific heat capacity of water, can be found in the linked article.
The high specific heat capacity of water is used, for example, in central heating systems. The temperature of the water in the radiator decreases only slightly when releasing heat to the surroundings. As a result, the radiator remains hot for a relatively long time. Due to the relatively low specific heat capacity of the ambient air of only 1 kJ/(kg⋅K), the temperature of the air thus increases more than the temperature of the water decreases (assuming the same mass)!
The great advantage of the high specific heat capacity of the water is also evident when taking a bath in the bathtub, as this keeps the water warm for a relatively long time. Likewise, the high specific heat capacity of water is used for water cooling systems – the cold water does not heat up as much despite the absorption of heat and thus retains its cooling effect for a relatively long time.
Specific heat capacity of gases
In contrast to incompressible substances such as solids and liquids, a distinction must be made for compressible substances such as gases as to whether heat is transferred at constant pressure (isobaric process, index “p”) or at constant volume (isochoric process, index “v”). With an isobaric process, more heat must be transferred in order to achieve a certain temperature change. The reason for this is that the transferred heat is not fully used to increase the temperature, but part of the (heat) energy it must be used to do work due to the expansion of the gas.
For this reason, the isobaric specific heat capacity cp is always larger than the isochoric specific heat capacity cv. The values for the isochoric specific heat capacities are given in round brackets in the table above. Note that in practice, a distinction between an isobaric and an isochoric heat transfer usually only needs to be made for compressible substances such as gases. More information on this can be found in the article Specific heat capacity of gases (at constant volume or pressure).







