Calorimeter to determine the specific heat capacities of liquids

Calorimetry deals with the measurement of heat energy.These measurements are based on temperature changes, which are used to determine the amount of heat involved.

Test setup

The experimental setups used in calorimetry are called calorimeters. Using an external heat supply, specific heat capacities of substances can be determined in calorimeters, especially of liquids. The measuring principle of such a measurement has already been explained in the article on specific heat capacity using the example of water. In the simplest case, a thermally insulated vessel is used so that heat losses to the surroundings can be kept as low as possible. The heat is supplied by a heating coil which is immersed in the liquid for which the specific heat capacity is to be determined.

With such a test setup it should be ensured that the liquid is heated evenly. Otherwise, the thermometer would only measure a punctual temperature which is not representative for the entire liquid. Without uniform heating, the temperature of the liquid near the heat source would be significantly higher than further away from it. Thus, during heating, the liquid should always be well mixed. This can be achieved by using a magnetic stirrer. In this case, the calorimeter stands on a plate that generates a rotating magnetic field. This rotating field causes a stir bar to rotate and thus mixes the liquid.

Taking heat losses into account

The heat supplied must be determined as accurately as possible in calorimeters in order to keep measurement uncertainties low. This can be done, for example, by an electrically operated heating coil. The easiest way to do this is to read off the electrical power directly from the power supply unit. However, the electrical power can also be determined via the voltage U applied to the heating coil and the current I flowing in it. The product of voltage and current is the electrical power of the heating coil P=U⋅I, which is completely converted into heat output (= heat energy released per unit time). The amount of heat Q emitted from the heater within the operating time t is then finally obtained from the product of the electrical power P and the time t:

\begin{align}
& Q = P \cdot t ~~~\text{where} ~~~P = U \cdot I ~~~\text{folgt:}  \\[5px]
\label{q}
& \boxed{Q = U \cdot I \cdot t} \\[5px]
\end{align}

In principle, heat transfer to the surroundings can be prevented by very good thermal insulation (at least for the duration of the experiment), but heating of the inside of the calorimeter cannot be prevented. The heat emitted by the heating coil will therefore always be transferred to the calorimeter to a certain extent and will not be completely absorbed by the water! Therefore, heat loss cannot be prevented. It is therefore important to take such heat losses into account. This is done by explicitly taking into account the absorption of heat by the calorimeter in the energy balance.

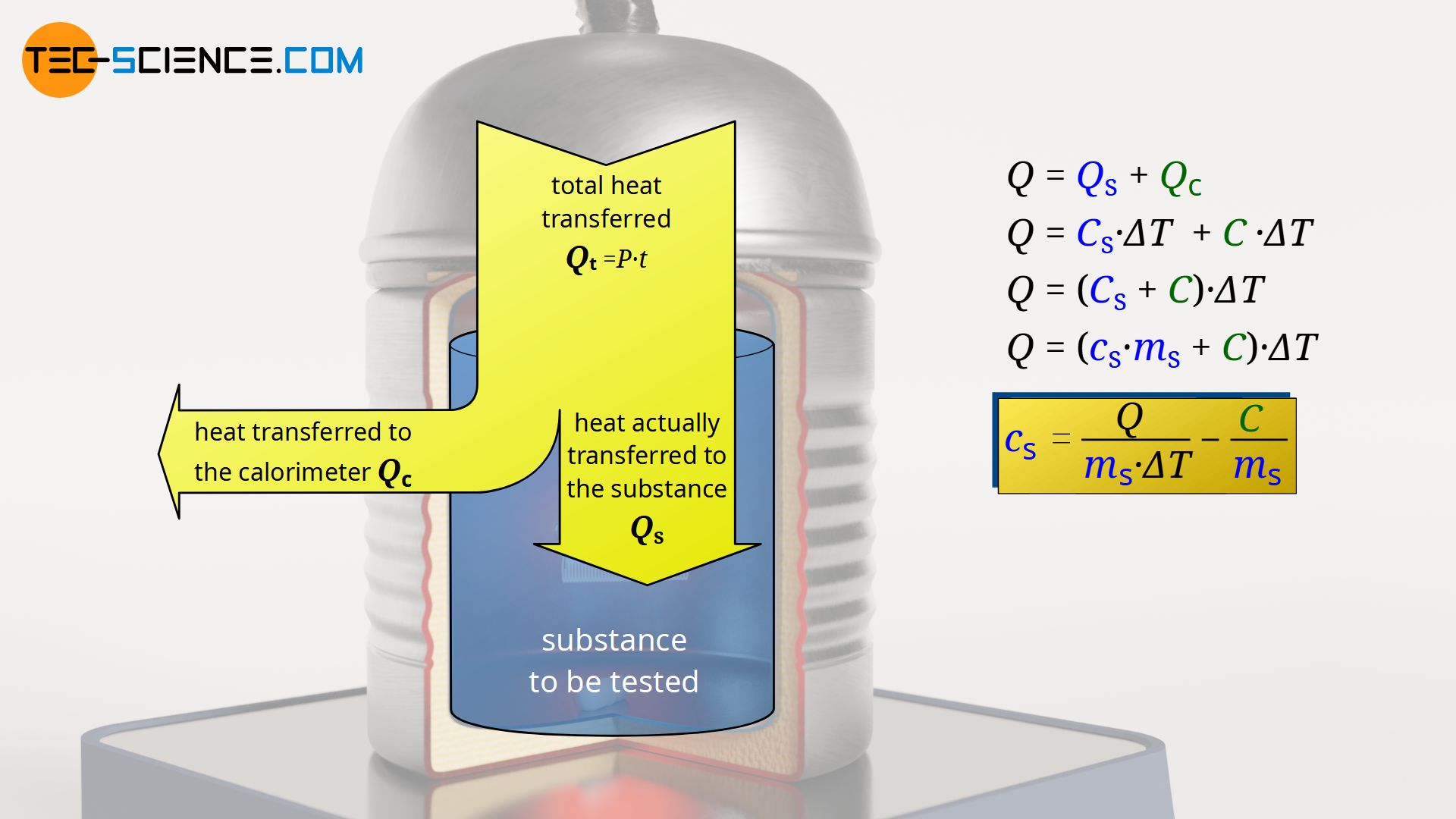
The heat energy Q_t emitted within the time t during the operation of the heating coil is transferred both to the substance to be tested (Q_s) (liquid) as well as to the calorimeter (Q_c). Thereby, both the temperature of the liquid and the temperature of the calorimeter increase by a certain amount ΔT:

\begin{align}
& Q_\text{t} = Q_\text{s} + Q_\text{c} \\[5px]
& Q_\text{t} = C_\text{s} \cdot \Delta T + C \cdot \Delta T ~~~~~\text{where }~~~ C_\text{s} = c_\text{s} \cdot m_\text{s} \\[5px]
\label{1}
& Q_\text{t} = c_\text{s} \cdot m_\text{s} \cdot \Delta T + C \cdot \Delta T \\[5px]
\end{align}

In this equation, C_s denotes the (absolute) heat capacity of the substance to be tested, which can also be expressed as the product of specific heat capacity c_s and mass m_s. The (absolute) heat capacity of the heated part of the calorimeter is denoted by C.

When heated slowly, the calorimeter will always assume the temperature of the liquid inside it. At identical initial temperatures, the temperature change ΔT of the substance to be tested is therefore also identical with that of the calorimeter (at least with that part of the calorimeter which heats up with the substance). Even with rapid heating, sooner or later a common mixing temperature will be reached between the calorimeter and the liquid, and thus the same temperature change will have occurred. The temperature change can therefore be factored out in equation (\ref{1}):

\begin{align}
& Q_\text{t} = \left( c_\text{s} \cdot m_\text{s} + C \right) \cdot \Delta T \\[5px]
\end{align}

The heat capacity C of the calorimeter can be determined in advance by mixing experiments (see next section). In this way, the specific heat capacity c_s of the liquid can finally be determined relatively accurately on the basis of the emitted heat Q_t and the temperature change ΔT:

\begin{align}
& Q_\text{t} = \left( c_\text{s} \cdot m_\text{s} + C \right) \cdot \Delta T \\[5px]
& \frac{Q_\text{t}}{\Delta T} = c_\text{s} \cdot m_\text{s} + C \\[5px]
& \frac{Q_\text{t}}{\Delta T} – C= c_\text{s} \cdot m_\text{s}  \\[5px]
\label{cs}
& \boxed{c_\text{s} = \frac{Q_\text{t}}{m_\text{s} \cdot \Delta T} – \frac{C}{m_\text{s}}}  \\[5px]
\end{align}

This formula can be interpreted as follows: Under real conditions, the specific heat capacity of the liquid c_s to be determined is lower by the term C/m_s than if ideal conditions were mistakenly assumed. For this ideal case, that the calorimeter does not absorb any heat, the heat capacity of the calorimeter is zero (C=0). This would then mean that no heat is needed to heat the calorimeter. The supplied heat Q_t would then actually benefit the liquid to be heated completely.

Heat capacity of the calorimeter (“water value”)

Definition of the “water value”

The determination of the heat capacity C of the calorimeter is essential if the specific heat capacities of liquids in calorimeters are to be determined as precisely as possible. The heat capacity C of a calorimeter is often referred to as “water value”, although historically this is not quite correct. The “water value” was originally understood to be the mass of water that has the same heat capacity as the calorimeter.

For example, if a calorimeter has a heat capacity of C = 42 J/K, the “water value” will be W = 10 g, since that mass of water has the same heat capacity of 42 J/K. This means that the calorimeter operates as if 10 g of water had to be heated in addition to the substance to be tested. However, the conceptual distinction is hardly made today, so that the “water value” in most cases (and also used in the following) is equivalent to the heat capacity of the calorimeter!

Determination of the heat capacity of the calorimeter

The heat capacity of a calorimeter C can be determined in advance by mixing experiments of water. The heating coil remains switched off the entire time! For this purpose, water of mass m₁ is first added to the calorimeter at room temperature. The calorimeter along with its contents (magnetic stir bar, temperature sensor, heating coil, etc.) and the water inside should then be given some time to allow their temperatures to equalize. After a certain time, a common initial temperature T₁ is reached (usually room temperature).

Now a second amount of water with mass m₂ with increased temperature T₂ is added to the calorimeter. A common mixing temperature between water of mass m₁, water of mass m₂ and the calorimeter will then be reached. Again, the system should be given some time to allow the temperatures to equalize. The temperature of the water will usually decrease slightly while reaching thermal equilibrium and that of the calorimeter will increase, because it is heated by the warm water. The resulting mixing temperature T_m is then measured. This now allows conclusions to be drawn about the heat capacity of the calorimeter.

For this purpose, the energy flow of the mixing process is considered in more detail. The entire system is ultimately heated by the warm water of mass m₂. The heat Q₂ emitted is divided into an amount of heat Q₁ which heats the cold water of mass m₁, and an amount of heat Q_c which heats the calorimeter. The heat energy Q₂ emitted by the water water of mass m₂ is determined by the temperature difference between the initial temperature T₂ and the final mixing temperature T_m. The absorbed heat energy Q₁ of the water mass m₁ is calculated in an analogous way. Likewise this applies to the absorbed heat Q_c of the calorimeter, where C is the unknown heat capacity of the calorimeter.

\begin{align}
Q_2 &= Q_1 + Q_\text{c}  \\[5px]
c_\text{w} \cdot m_2 \cdot (T_2-T_\text{m}) &=  c_\text{w} \cdot m_1 \cdot (T_\text{m}-T_1) + C \cdot (T_\text{m}-T_1)  \\[5px]
\end{align}

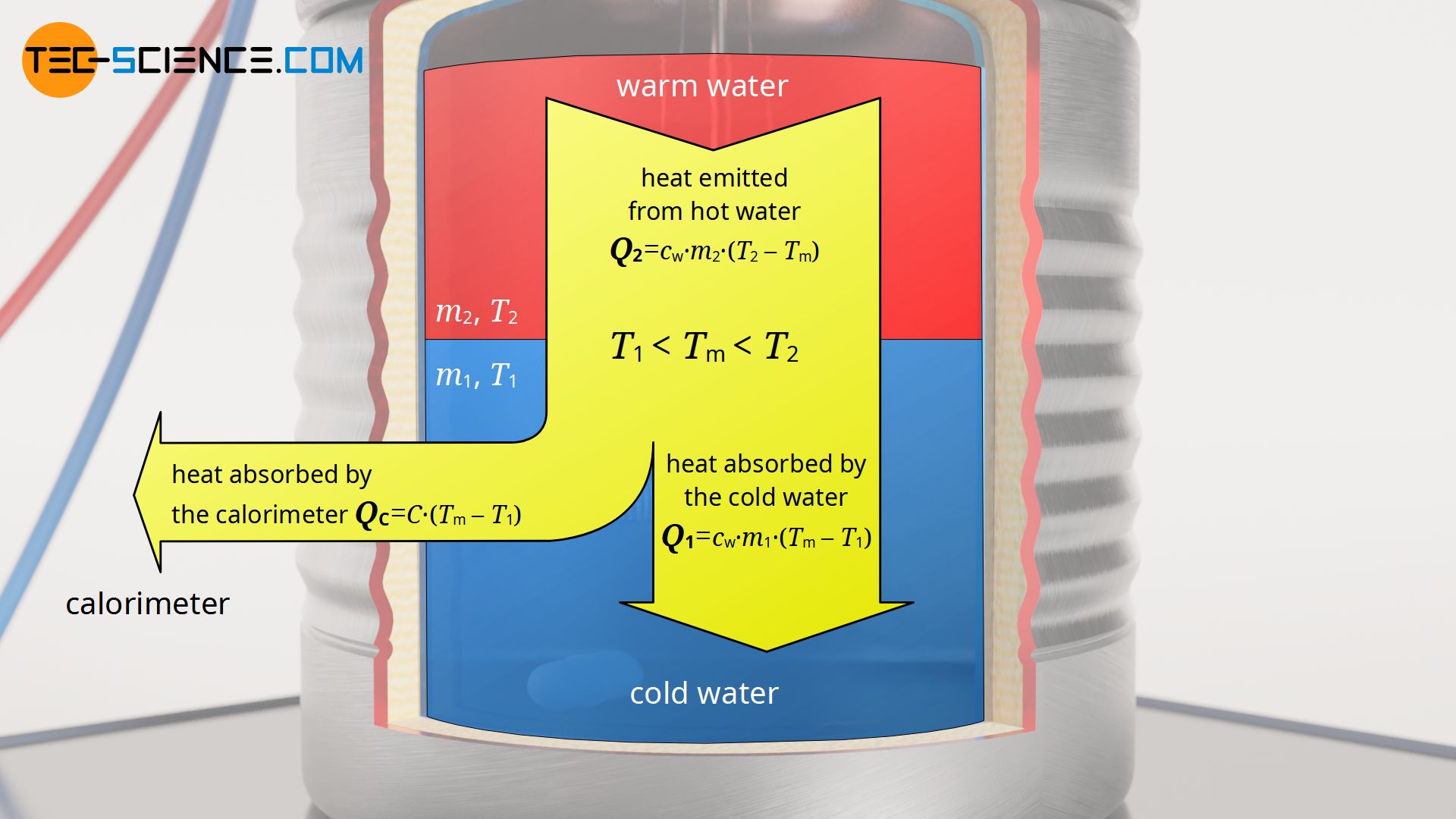
In this equation, c_w denotes the specific heat capacity of water with c_w=4.187 kJ/(kg⋅K). Thus, the only unknown quantity in this equation is the heat capacity C of the calorimeter (“water value”). After solving this equation for C, the heat capacity of the calorimeter can finally be determined as follows:

\begin{align}
&\boxed{C = c_\text{w} \left( m_2 \frac{T_2-T_\text{m}}{T_\text{m}-T_1}-m_1   \right)}  ~~~\text{heat capacity of the calorimeter} \\[5px]
\end{align}

The heat capacity of the calorimeter determined in this way can now be used in equation (\ref{cs}) to determine as precisely as possible the actual specific heat capacity of the liquid to be tested in further experiments.

Note: According to the historical definition of the “water value” W – i.e. as equivalent water mass having the same heat capacity as the calorimeter – that quantity C would still have to be divided by the specific heat capacity of water c_w:

\begin{align}
&\boxed{W =  m_2 \frac{T_2-T_M}{T_M-T_1}-m_1 }  ~~~\text{“water value” (historical definition)} \\[5px]
\end{align}

Influencing factors on the heat capacity of the calorimeter

Note that the heat capacity C of the calorimeter is not a constant parameter! It depends on the following influencing factors:

Liquid level: If, for example, the calorimeter is only half filled with liquid during testing, not the entire apparatus may be heated. The heated mass of the calorimeter is lower and thus also the heat capacity of the calorimeter.

Test duration: The test duration also influences the heat capacity of the calorimeter. For example, longer testing times can also heat up more of the calorimeter (more mass) than shorter measurement runs. The heat capacity of the calorimeter will be greater in this case.

Temperature: In a similar way, the temperature at which the experiment is carried out also influences the heat capacity of the calorimeter. This is because at higher temperatures, the rate of heat flow onto the calorimeter also increases. This leads to the fact that the calorimeter can heat up more in the same time and thus also more of the calorimeter (more mass) will be affected by the heating – the heat capacity of the calorimeter increases. In extreme cases, high temperatures in combination with very long measurement runs can also cause heat to penetrate the calorimeter and thus be transferred to the surroundings!

Due to the influencing factors mentioned above, the heat capacity of the calorimeter should therefore be determined in advance under conditions similar to those that will later be present during the actual measurement. This means in particular:

• similar liquid levels,
• similar temperatures,
• similar testing times.

The heat capacity of a calorimeter is a TEST SPECIFIC heat capacity and not THE heat capacity of the calorimeter!

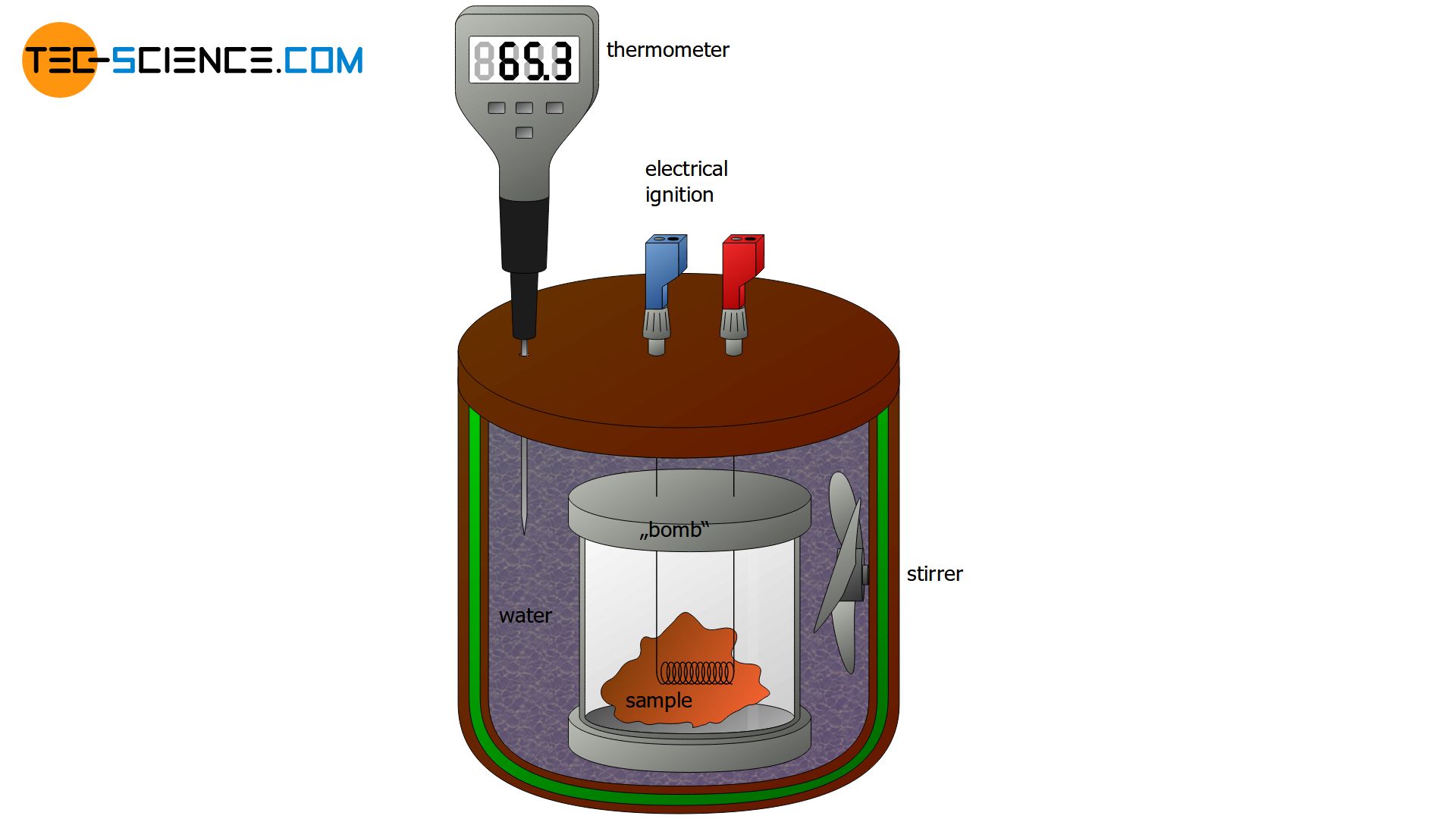
Bomb calorimeter

A special type of calorimeter is the so-called bomb calorimeter. A bomb calorimeter is used, for example, to determine the energy content of food. To do this, the sample to be analyzed is first placed in a vessel known as a bomb. The bomb is then filled with oxygen and placed under high pressure. This bomb is now placed in a water bath inside the calorimeter. Electrical energy is used to ignite the sample, similar to the ignition of a bomb, which gives this calorimeter its name. The temperature increase of the water bath can then be used to calculate the heat released by the combustion of the sample (= energy content of the food).