Definition der spezifischen Wärmekapazität
Die spezifische Wärmekapazität c beschreibt den Zusammenhang zwischen einer Wärmezufuhr Q und der damit verbundenen Temperaturerhöhung ΔT eines Stoffes der Masse m:
\begin{align}
\label{q}
& \boxed{Q = c \cdot m \cdot \Delta T} \\[5px]
\end{align}
Im Artikel Spezifische Wärmekapazität (Herleitung und Definition) ist die Herleitung dieser Formel exemplarisch am Beispiel der Erwärmung von Wasser gezeigt. Im Folgenden werden Gültigkeitsbereiche und wichtige Einschränkungen dieser Formel näher erläutert.

Wärmeverluste
Bei der experimentellen Bestimmung der spezifischen Wärmekapazität von Wasser durch Erwärmung mit einem Tauchsieder wird grundsätzlich ein größerer Wert ermittelt als der Stoff tatsächlich besitzt.

Grund hierfür ist, dass die vom Tauchsieder abgegebene Wärme nicht vollständig dem Wasser zugeführt wird. Ein Teil dieser Wärme wird auch zur Erwärmung des Gefäßes und der Umgebung genutzt. Damit kommt dem Wasser nur eine geringere Wärmeenergie als theoretisch berechnet zugute. Mehr Informationen hierzu und eine Möglichkeit zur Vermeidung dieses systematischen Fehlers finden sich im Artikel Kalorimeter zur Ermittlung der spezifischen Wärmekapazitäten von Flüssigkeiten.
Erwärmung vs. Abkühlung
Wie bereits angemerkt, wurde Formel (\ref{q}) anhand einer Erwärmung hergeleitet. Dieser Zusammenhang zwischen Wärme und Temperaturänderung gilt aufgrund der Energieerhaltung aber auch für eine Abkühlung, bei die Temperatur um einen bestimmten Betrag ΔT gesenkt werden soll. Hierzu muss der entsprechende Wärmebetrag Q, der sich ebenso nach Gleichung (\ref{q}) ermittelt, dem Stoff entzogen werden.

Da die Temperaturänderung bei Abkühlung mathematisch betrachtet negativ ist, erhält man für den Wärmeumsatz ebenfalls ein negatives Vorzeichen. Das Vorzeichen im Ergebnis des Wärmeumsatzes gibt also an, ob einem Stoff Wärme zu- oder abgeführt wird. Ein positives Vorzeichen bedeutet, dass der Wärmebetrag dem Stoff zugeführt werden muss. Entsprechend ist bei einem negativen Vorzeichen dem Stoff jener Wärmebetrag zu entziehen.
Die spezifische Wärmekapazität beschreibt nicht nur für eine Erwärmung den Zusammenhang zwischen Wärme und Temperaturänderung, sondern auch für eine Abkühlung!
Einschränkung der Gültigkeit bei Aggregatzustandsänderungen
Formel (\ref{q}) ist grundsätzlich nur solange gültig, solange sich der Aggregatzustand eines Stoffes nicht ändert. Bei Phasenübergängen gilt der Zusammenhang zwischen Wärmeumsatz und Temperaturänderung in dieser Form nicht mehr! Dies zeigt bereits die Alltagserfahrung beim Kochen von Wasser. Beim Siedevorgang des Wassers verharrt die Temperatur trotz stetiger Wärmezufuhr bei 100 °C, bis irgendwann alles Wasser verdampft ist. Ein Zusammenhang gemäß Gleichung (\ref{q}) zwischen Wärmezufuhr und Temperaturänderung gibt es in dieser Form bei Phasenübergängen also nicht mehr!

Die spezifische Wärmekapazität hat ihre Gültigkeit nur solange kein Phasenübergang (Aggregatzustandsänderung) eintritt!
Natürlich muss auch bei einem Phasenübergang Wärme zu- oder abgeführt, um den Prozess der Aggregatzustandsänderung voran zu treiben. Die Berechnung solcher latenten Wärmeumsätze ist im Artikel Spezifische Verdampfungswärme (latente Wärme) näher beschrieben.
Abhängigkeit der spezifischen Wärmekapazität vom Aggregatzustand und von der Temperatur
Die spezifische Wärmekapazität ist tatsächlich keine reine Stoffkonstante, sondern hängt entscheidend vom Aggregatzustand ab. So sinkt bspw. die spezifische Wärmekapazität von Wasser um rund die Hälfte, wenn sich das Wasser nicht mehr im flüssigen Zustand befindet, sondern im gasförmigen Zustand. Gasförmiges Wasser liegt bspw. in den Rohrleitungen von Dampfkraftwerken vor, bei denen das Wasser teilweise auf über 500 °C erwärmt wird (sog. Frischdampftemperatur).
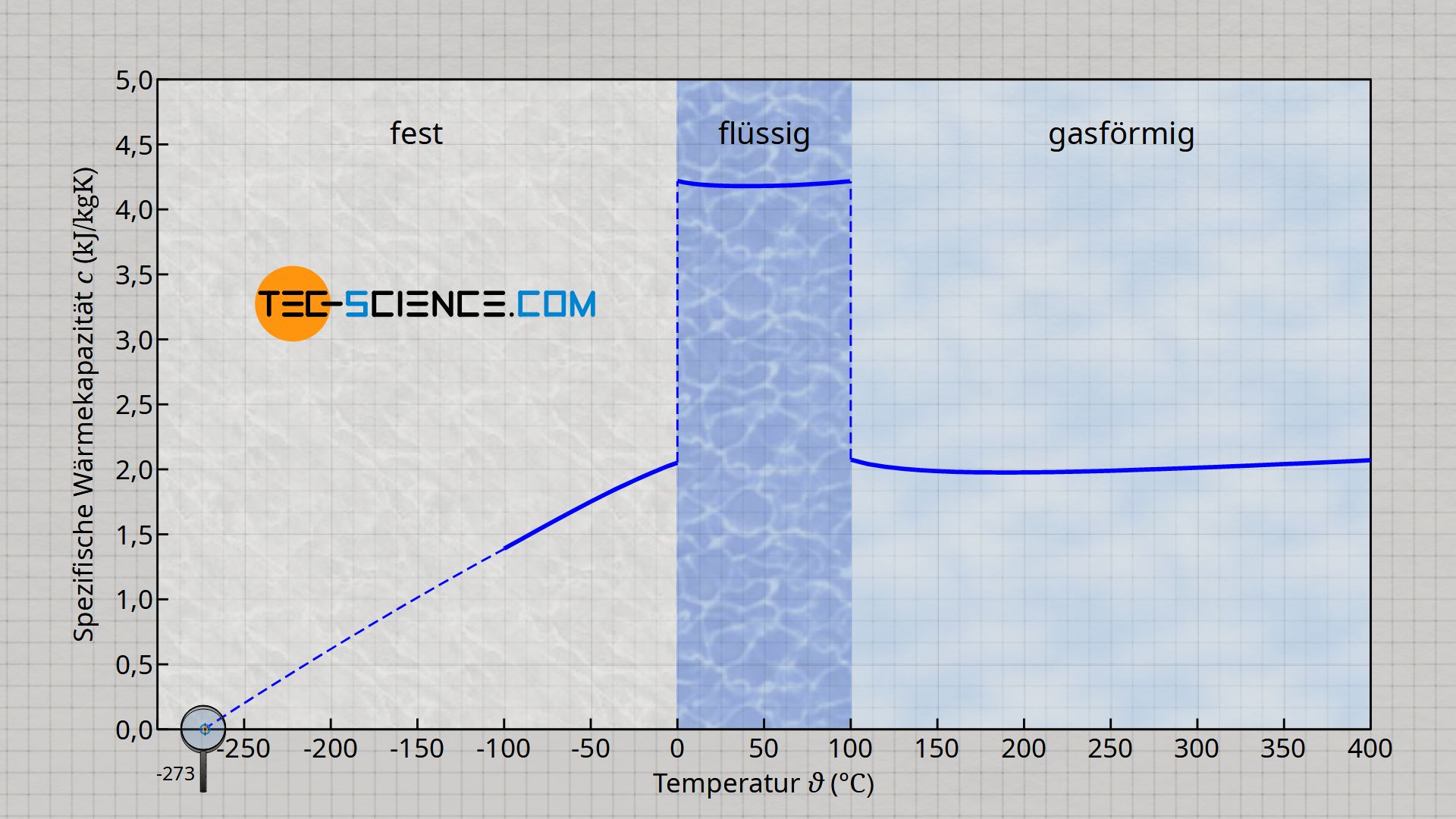
Zudem kann die spezifische Wärmekapazität mehr oder weniger stark von der Temperatur abhängen. Bei Wasser ist eine solche Temperaturabhängigkeit vor allem im festen Zustand (Eis) gegeben. Bis hin zum absoluten Nullpunkt nimmt die spezifische Wärmekapazität des Eises kontinuierlich ab. Mehr Informationen hierzu finden sich im Artikel Spezifische Wärmekapazität von Wasser.
Abhängigkeit der spezifischen Wärmekapazität vom Prozess der Wärmezufuhr
Bei der Erwärmung oder Abkühlung eines Stoffes muss im Allgemeinen unterschieden werden, ob Wärme bei konstantem Druck (isobarer Prozess) oder bei konstantem Volumen (isochorer Prozess) übertragen wird. Je nach Prozess unterscheidet sich nämlich die spezifische Wärmekapazität und somit auch der Betrag der Temperaturänderung, die durch einen bestimmte Wärmemenge hervorgerufen wird.
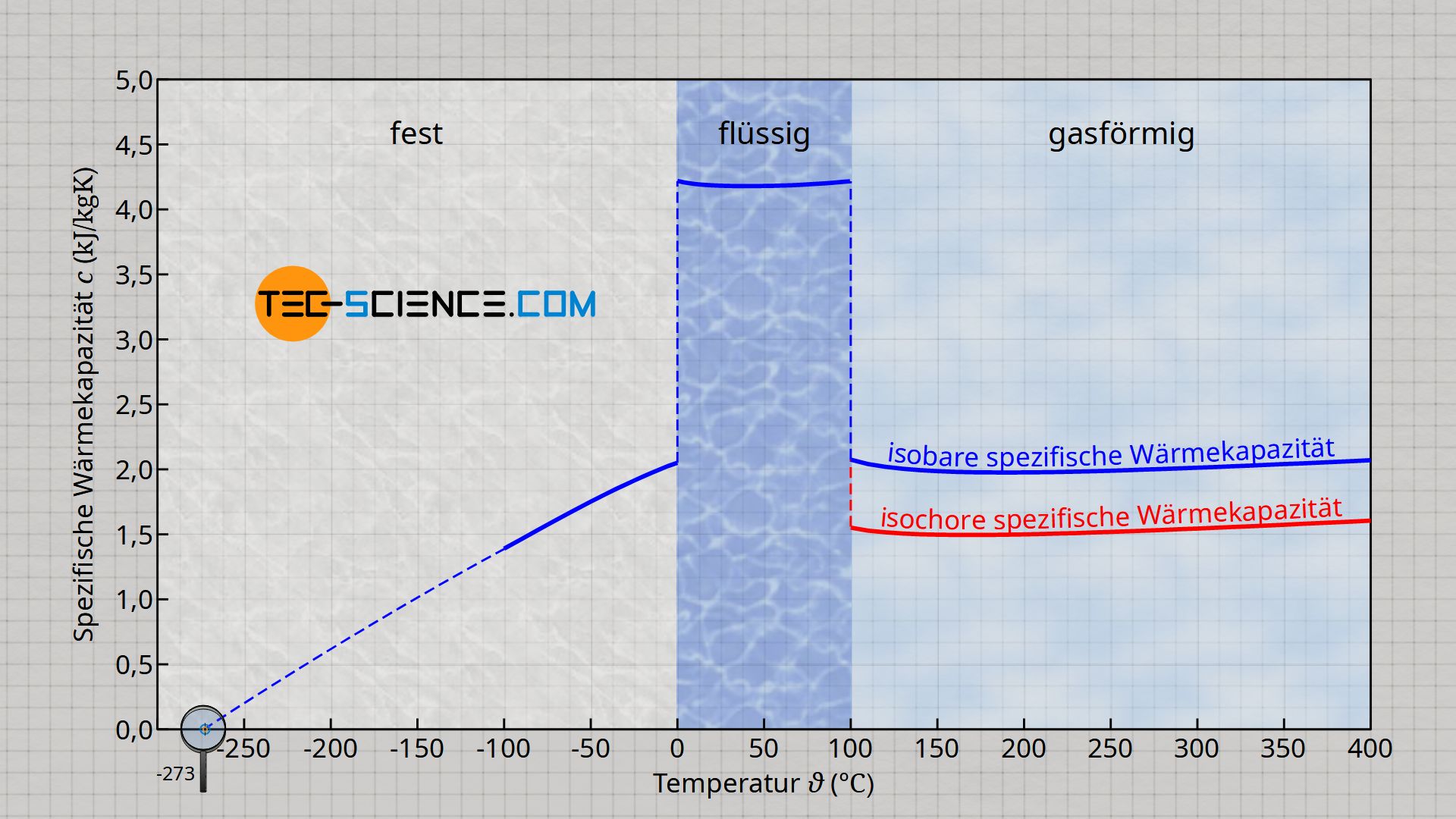
Bei einer isobaren Wärmezufuhr muss grundsätzlich mehr Wärme für dieselbe Temperaturerhöhung zugeführt werden, da die Wärmeenergie nicht vollständig für eine Temperaturerhöhung genutzt wird (Erhöhung der inneren Energie), sondern ein gewisser Teil in Arbeit umgewandelt wird, die für die Ausdehnung des Stoffes benötigt wird. Bei einem isochoren Prozess kann die Wärmezufuhr hingegen vollständig zur Temperaturerhöhung genutzt werden. Somit erfolgt dieselbe Temperaturänderung bereits bei einem geringeren Wärmeumsatz.
Aus diesem Grund unterscheidet man die spezifische Wärmekapazität des isochoren Prozesses cv und die spezifische Wärmekapazität des isobaren Prozesses cp, wobei stets gilt: cp>cv. Diese Unterscheidung ist vor allem bei kompressiblen Stoffen wie Gasen der Fall, die ihr Volumen sehr stark mit der Temperatur ändern. Mehr Informationen hierzu im Artikel Spezifische Wärmekapazität von Gasen (bei konstantem Druck bzw. Volumen).
Bei inkompressiblen Stoffen wie Festkörper und Flüssigkeiten, muss eine solche Unterscheidung zwischen isobarer und isochorer Wärmezufuhr meist nicht getroffen werden. Zum Einen ändern diese Stoffe ihr Volumen bei Wärmezufuhr oder Wärmeabfuhr nur geringfügig, sodass sich beide Werte oft kaum voneinander unterscheiden. Zum Anderen findet bei diesen Stoffen eine Wärmeübertragung ohnehin meist unter der Bedingung statt, dass sich diese frei ausdehnen können. Die Wärmezufuhr oder Wärmeabfuhr findet somit in der Regel bei konstantem Umgebungsdruck statt und entspricht damit einem isobaren Prozess. Bei Flüssigkeiten und Feststoffen ist also ohnehin meist nur die spezifische Wärmekapazität des isobaren Prozesses relevant, die dann der Einfachheit halber lediglich mit c bezeichnet wird.
Irreführende Begrifflichkeit der „Kapazität“
Der Begriff Kapazität soll im Zusammenhang mit der spezifischen Wärmekapazität das Vermögen eines Gegenstandes beschreiben, Wärmeenergie aufzunehmen, ohne dass sich dabei die Temperatur merklich ändert. Also ein sehr hohes Wärmeaufnahmevermögen ohne große Temperaturänderung.
Der Begriff Kapazität ist insofern etwas unglücklich gewählt, da es sich bei dem Wärmebegriff thermodynamisch gesehen nicht um eine Zustandsgröße, sondern um eine sogenannte Prozessgröße handelt. Es gibt im thermodynamischen Sinne keine Kapazität im Sinne einer Speicherung von Wärme! Die zugeführte Wärmeenergie wird letztlich in innerer Energie gespeichert bzw. wird auf Kosten der inneren Energie dem Gegenstand bei Abkühlung wieder entzogen.
Die Kalorie
Die heute zwar noch gebräuchliche aber nicht mehr zulässige physikalische Größe Kalorie im Zusammenhang mit dem Energieinhalt von Nahrungsmitteln hat ihren Ursprung in der Erwärmung des Wassers. Dabei definierte man jene Energiemenge die nötig ist um 1 g Wasser um 1 °C zu erhöhen als 1 Kalorie (1 cal). Demnach entspricht also 1 cal einer Energiemenge von 4,2 J.
Die Kalorie ist eine veraltete Energieeinheit und entspricht jener Energiemenge, die Wasser der Masse 1 g um 1 °C erwärmt (1 cal ≙ 4,2 J)!
Die häufiger verwendete Einheit in der Nahrungsmittelindustrie ist die Kilokalorie (kcal), die folglich einem Energiewert von 4,2 kJ entspricht. ACHTUNG: Häufig ist im Zusammenhang mit Nahrungsmitteln nur von Kalorien die Rede ist, obwohl in den meisten Fällen jedoch Kilokalorie gemeint ist!