The Schmidt-number is a dimensionless similarity parameter to describe transport of mass and momentum.
Not only the transport of momentum and the heat transfer influence each other as already explained in detail in the article on the Prandtl number. Momentum transport and mass transfer also interact with each other. Among other things, the momentum transport is due to Brownian motion. In this way, fluid particles diffuse across the fluid layers and have to adapt to the new velocities, so to speak (transfer of momentum). If there is also a concentration gradient, the fluid particles diffuse into other fluid layers not only due to the random Brownian motion, but also due to the concentration gradient.
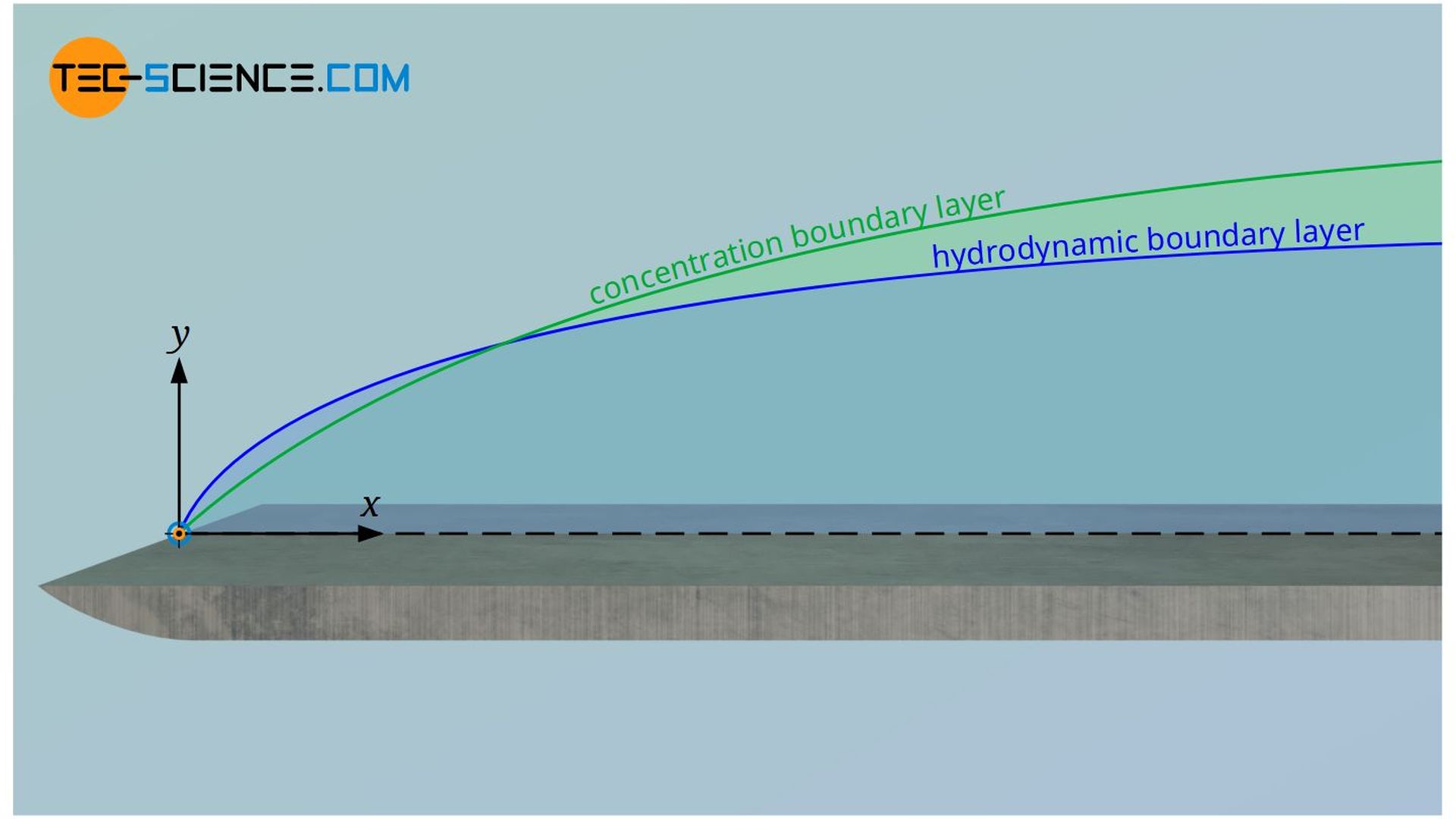
The ratio of momentum and mass transfer is expressed by the so-called Schmidt number Sc. It is, so to speak, a measure for the ratio of the boundary layer thicknesses between hydrodynamic boundary layer and concentration boundary layer. The Schmidt number puts the viscosity ν of a fluid in relation to its diffusion coefficient D:
\begin{align}
&\text{Schmidt number} = \frac{\text{transport of momentum}}{\text{transport of mass}} \\[5px]
\label{sc}
&\boxed{Sc = \frac{\nu}{D}} ~~~~~\text{Schmidt number}\\[5px]
\end{align}
The Schmidt number can be considered analogous to the Prandtl number. While the Prandtl number describes the diffusion of heat, the Schmidt number characterizes the diffusion of matter. In the same way that the Prandtl number is used to determine the Nusselt number as a dimensionless heat transfer coefficient, the Schmidt number is used to determine the Sherwood number, which has its significance as a dimensionless mass transfer coefficient. Both dimensionless transfer numbers (Nusselt number and Sherwood number) also have in common that they are influenced by the Reynolds number Re.
| heat transfer | mass transfer | |
| characteristic parameter | Prandtl number | Schmidt number |
| diffusion of … | heat | matter |
| affects the … | dimensionless heat transfer coefficient | dimensionless mass transfer coefficient |
| dimensionless transfer number | Nusselt number Nu = f(Sc, Re) | Sherwood number Sh = f(Pr, Re) |
Just like the Prandtl number, the Schmidt number is also a dimensionless similarity parameter. This means that mass and momentum transport in two differently sized systems are only physically similar if the Schmidt numbers are identical. Only then, for example, is it possible to transfer the knowledge gained in a model experiment to real applications.
The Schmidt number is a dimensionless similarity parameter to describe mass and momentum transfer. Only with identical Schmidt numbers one obtains physically similar mass and momentum transfers, independent of the size of the system.






