The thermal conductivity of ideal gases is not dependent on pressure for gases that are not too strongly diluted. This is no longer the case for gases with low pressure.
Introduction
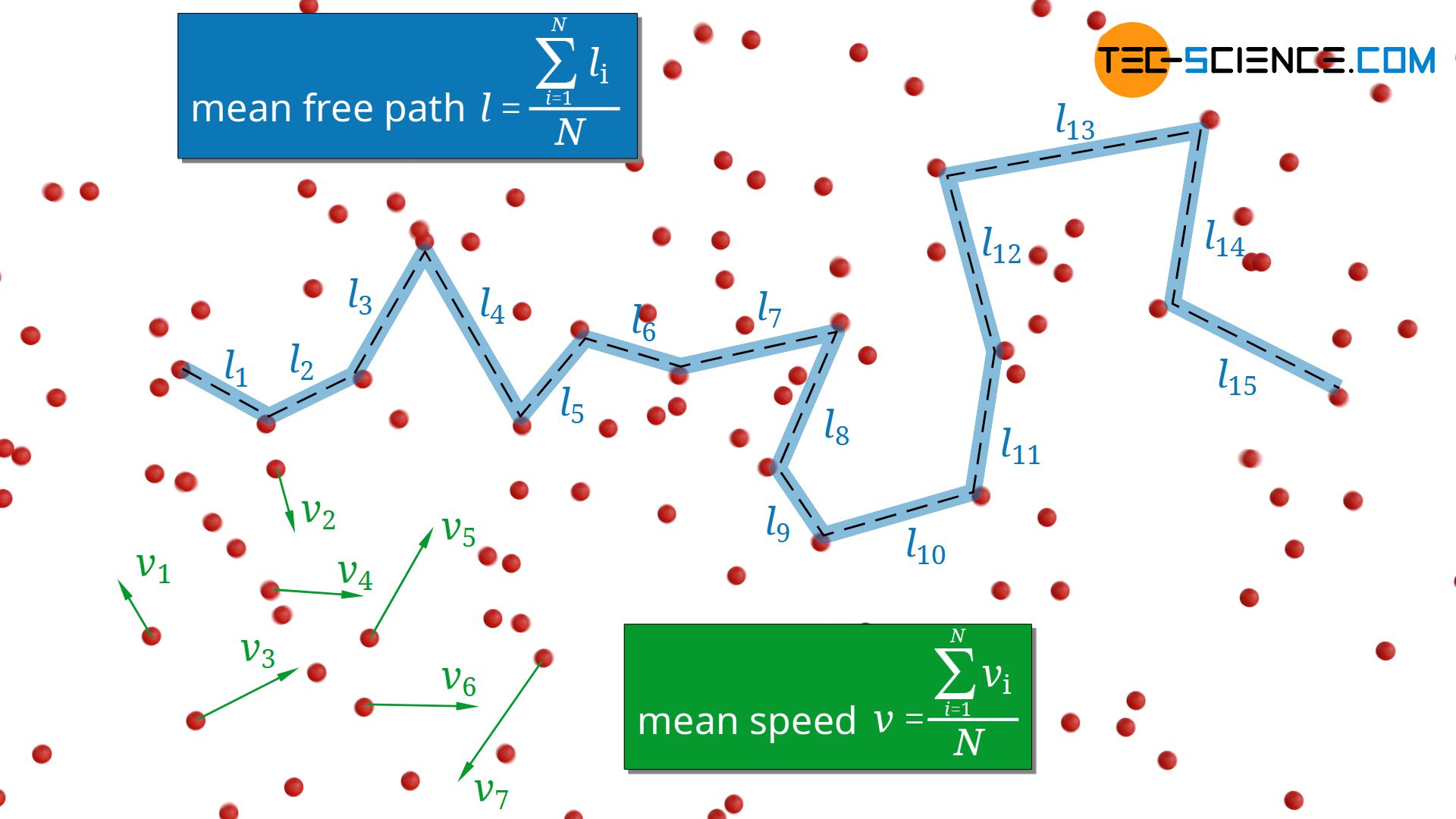
In the article Thermal conduction in solids and ideal gases, the following formula for estimating the thermal conductivity λ of ideal gases was derived:
\begin{align}
\label{l}
& \boxed{\lambda = \frac{1}{3} \cdot c_v \cdot \rho \cdot v \cdot l} \\[5px]
\end{align}
In this formula cv denotes the specific heat capacity at constant volume, ϱ the density of the gas, v the mean speed of the gas molecules and l the mean free path. This formula will be explained in more detail in this article and the resulting conclusions for gases will be discussed.
Using the formula, one could assume that the thermal conductivity depends on the pressure, because the higher the pressure, the higher the density of the gas. This argument can also be clearly understood with the help of the particle model of matter, because the more particles there are, the more energy the particles can transport in total. Note that according to the kinetic theory of gases each gas molecule carries the energy ½⋅kB⋅T per degree of freedom (with kB as the Boltzmann constant).
However, to the same extent as the density increases with increasing pressure, the mean free path decreases! In fact, the thermal conductivity of ideal gases is therefore independent of pressure or particle density (for the limitation of this statement, later more)!
The thermal conductivity of gases is not dependent on pressure for not too low pressures!
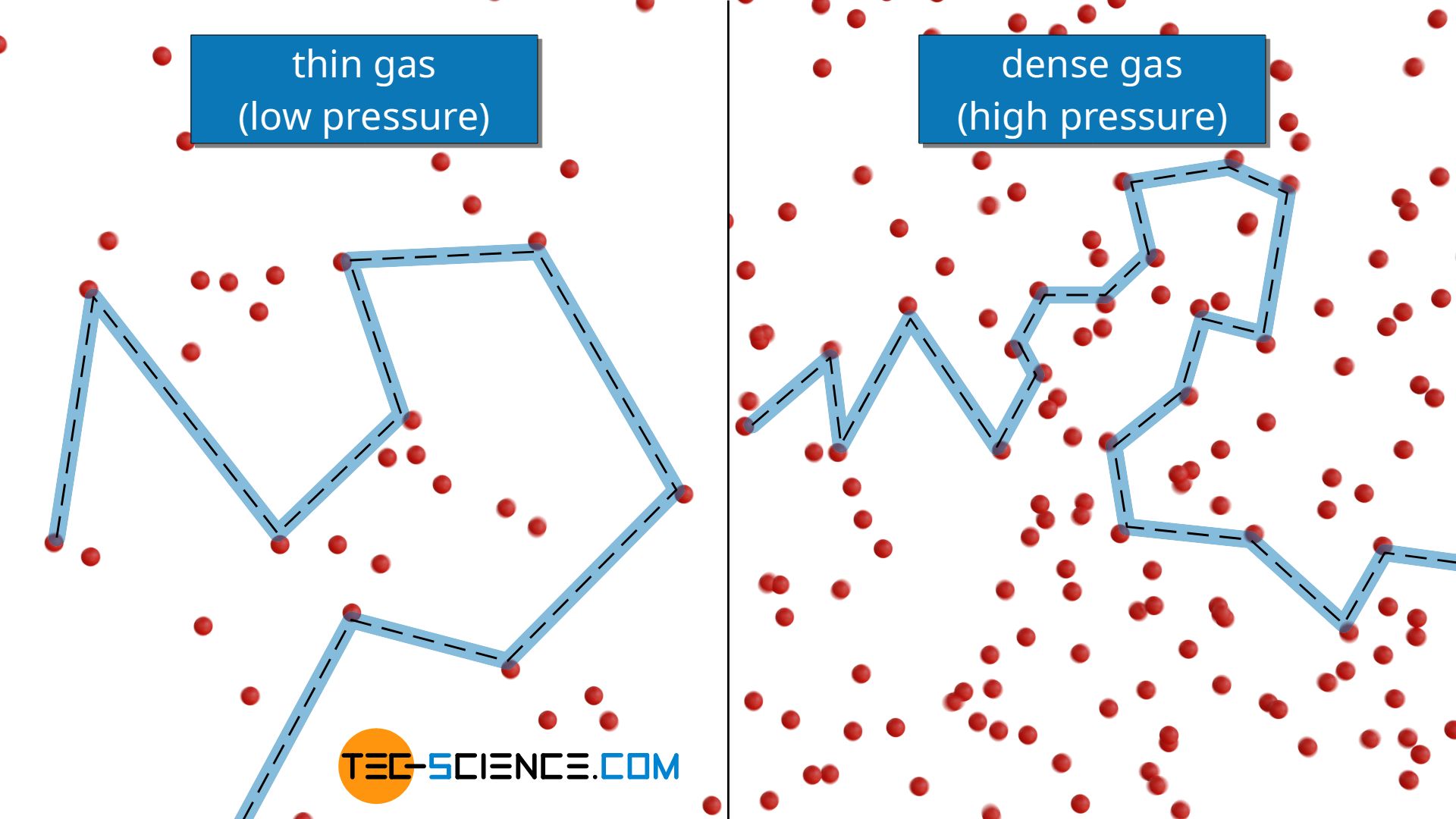
Independence of thermal conductivity from pressure for high pressures (dense gases)
The independence of thermal conductivity from pressure can also be shown mathematically. For this purpose the density ϱ in equation (\ref{l}) is first expressed by the quotient of gas mass mgas and gas volume Vgas. Then the gas mass can be expressed by the amount of substance ngas (chemical amount) and the molar mass Mgas of the gas.
\begin{align}
\lambda &= \frac{1}{3} \cdot c_v \cdot \frac{m_{gas}}{V_{gas}} \cdot v \cdot l \\[5px]
&= \frac{1}{3} \cdot c_v \cdot \frac{n_{gas} \cdot M_{gas}}{V} \cdot v \cdot l \\[5px]
\end{align}
The product of mass-specific heat capacity and molar mass equals the so-called molar heat capacity Cm,v, whereby the molar heat capacity is only dependent on the degrees of freedom f and the molar gas constant Rm (Cm,v=f/2⋅Rm). In addition, the amount of substance ngas can be expressed by the ratio of the number of particles N and Avogadro constant NA (ngas=N/NA):
\begin{align}
\lambda &= \frac{1}{3} \cdot \underbrace{c_v \cdot M_{gas}}_{C_{m,v}} \cdot \frac{n_{gas}}{V} \cdot v \cdot l \\[5px]
& = \frac{1}{3} \cdot \underbrace {C_{m,v}}_{=\frac{f}{2}R_m} \cdot \frac{N}{N_A \cdot V} \cdot v \cdot l \\[5px]
& = \frac{1}{3} \cdot \frac{f}{2} R_{m} \cdot \frac{1}{N_A} \cdot \frac{N}{V} \cdot v \cdot l \\[5px]
& = \frac{f}{6} \frac{R_m}{N_A} \cdot \frac{N}{V} \cdot v \cdot l \\[5px]
\end{align}
The ratio of particle number and gas volume corresponds to the particle density n and the quotient of molar gas constant and Avogadro constant corresponds to the Boltzmann constant kB (for this relationship see article Internal Energy & Heat Capacity):
\begin{align}
\lambda & = \frac{f}{6} \underbrace{\frac{R_m}{N_A}}_{k_B} \cdot \underbrace{\frac{N}{V}}_{n} \cdot v \cdot l \\[5px]
\label{ll}
& = \frac{f}{6} k_B \cdot n \cdot v \cdot l \\[5px]
\end{align}
Now we only need the dependencies of the mean speed and the mean free path. According to the Maxwell-Boltzmann distribution, the mean speed v of the gas molecules depends on the temperature T of the gas and the mass m of a molecule (m denotes the mass of a single gas particle and not the entire gas mass!)
\begin{align}
& \boxed{v = \sqrt{\frac{8 k_B T}{\pi m}}} \\[5px]
\end{align}
The mean free path l of the molecules depends not only on the particle density n but also on the particle diameter d and is determined by the following formula:
\begin{align}
& \boxed{l= \frac{1}{\sqrt{2} n \pi d^2}} \\[5px]
\end{align}
If both formulas are used in equation (\ref{ll}), the thermal conductivity can be determined with the following formula:
\begin{align}
& \lambda = \frac{f}{6} k_B \cdot n \cdot v \cdot l \\[5px]
& \lambda = \frac{f}{6} k_B \cdot n \cdot \sqrt{\frac{8 k_B T}{\pi m}} \cdot \frac{1}{\sqrt{2} n \pi d^2} \\[5px]
\require{cancel}
& \lambda = \frac{f}{6} k_B \cdot \cancel{n} \cdot \sqrt{\frac{8 k_B T}{\pi m}} \cdot \frac{1}{\sqrt{2} \cancel{n} \pi d^2} \\[5px]
& \lambda = \frac{f}{6} k_B \cdot \sqrt{\frac{8 k_B T}{\pi m}} \cdot \frac{1}{\sqrt{2} \pi d^2} \\[5px]
& \boxed{\lambda = \frac{f}{3d^2} \sqrt{\frac{k_B^3 T}{\pi^3 m }}} \\[5px]
\end{align}
This formula now clearly shows that the thermal conductivity of ideal gases is not dependent on particle density and thus not on pressure. It also shows that gases with relatively large molecules have a lower thermal conductivity than gases with smaller molecules (this is due to the decrease in the mean free path resulting from the larger collision diameter d). Furthermore, the thermal conductivity of gases with light particles is higher than that of gases with heavier particles. Furthermore, the thermal conductivity depends on the temperature. The thermal conductivity increases with increasing temperature!
The thermal conductivity of gases is the greater, the smaller and lighter the molecules are and the higher the temperature is!
Dependence of thermal conductivity from pressure for low pressures (diluted gases)
If pressure has no influence on the thermal conductivity of gases, why use a vacuum for thermal insulation?
The fact that thermal conductivity does not depend on pressure is only true as long as the mean free path is much smaller than the dimensions of the volume in which the gas is contained. If the pressure (particle density) in a container is reduced more and more, the particles no longer collide with each other, but rather with the container walls. At very low pressures, the mean free path is thus determined by the dimension of the container and no longer by the free path between two particle collisions.
This also applies if the pressure is not reduced, but the container dimension is. This is relevant, for example, for insulating materials where gases are enclosed in small pores. Such situations can also occur with thin layers of foil or small gaps if there is a gas in between.
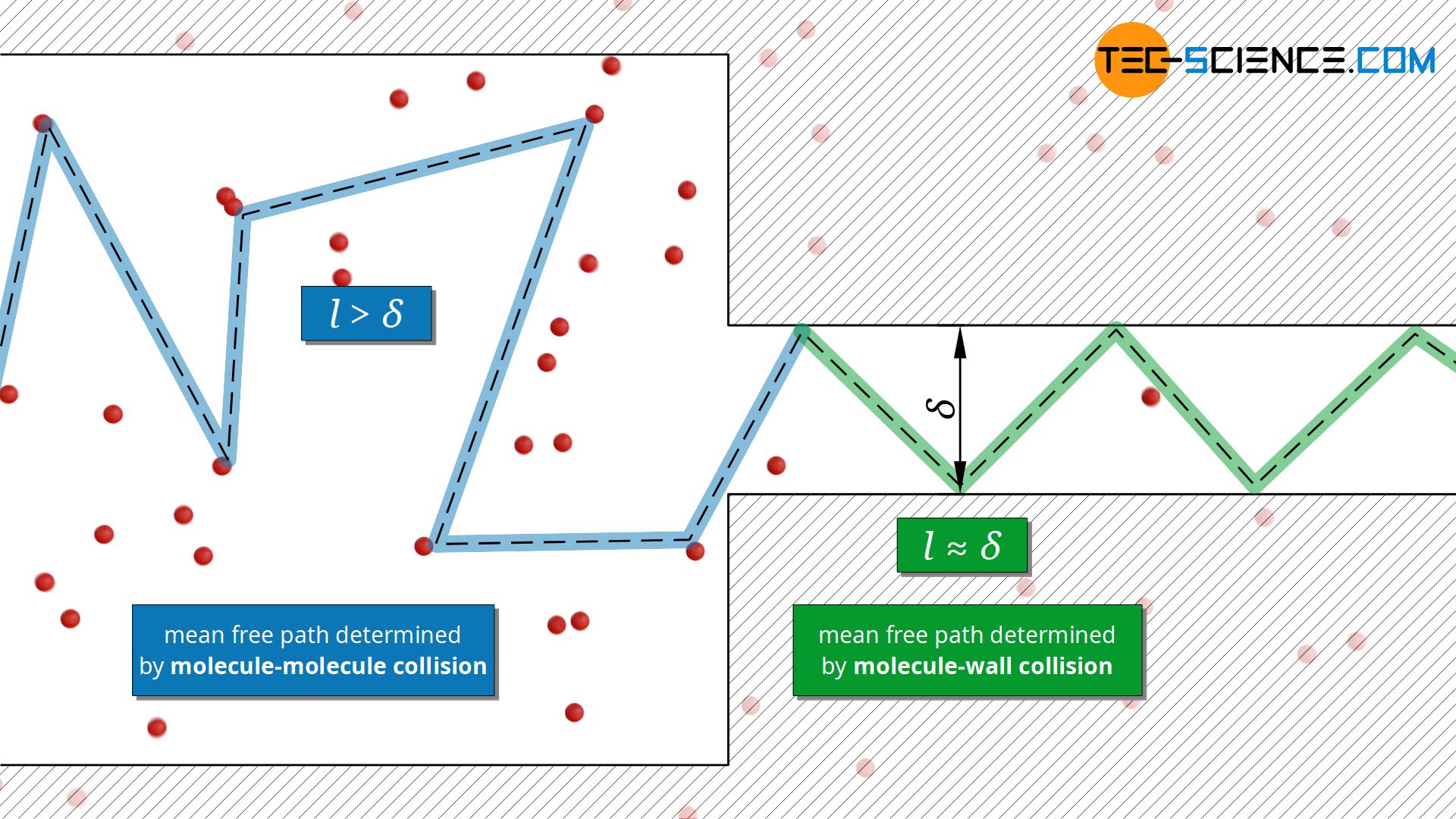
The mean free path in these cases corresponds approximately to the dimension δ of the volume (e.g. pore diameter or gap distance) and is therefore a constant value. In this case the mean free path is no longer dependent on the particle density: l≈δ=constant. With the mean free path as a constant, equation (\ref{ll}) then indicates a reduction of the thermal conductivity with decreasing particle density (or pressure)!
\begin{align}
\label{a}
&\lambda = \frac{f}{6} k_B \cdot n \cdot v \cdot \delta \\[5px]
\end{align}
In diluted gases or with small gas volumes, the thermal conductivity depends on the pressure!
In so-called Pirani gauges, this relationship is used to draw conclusions about the pressures in a high vacuum environment on the basis of thermal conductivity.
Knudsen number
As already indicated, the characteristic length δ of the pores or the foil spacing in insulation materials is often much smaller than the mean free path l of the gases contained therein. In this case the gas can no longer be described as a continuum, so that equation (\ref{a}) can no longer be applied in this form (the qualitative statement of this equation does not lose its validity, however).
The characteristic length refers to the dimension/size of a system!
In this context, the so-called Knudsen number indicates whether the gas can still be regarded as a continuum or whether the kinetics of the gas theory must be applied. The unitless Knudsen number Kn describes the ratio of the mean free path l to the characteristic length δ of the gas volume:
\begin{align}
&\boxed{Kn := \frac{l}{\delta}} \\[5px]
\end{align}
For values much smaller than 1, continuum mechanics still applies and for values much larger than 1 the description by means of the laws of kinetic gas theory are used.
Since for ideal gases the mean free path can be expressed not only by the particle density but also by the pressure p using the ideal gas law (see article here), the Knudsen number can be determined as follows from the pressure and temperature (d describes the diameter of the gas molecules):
\begin{align}
&\boxed{Kn = \frac{k_B \cdot T}{\sqrt{2}\pi \cdot d^2 \cdot p \cdot \delta}} \\[5px]
\end{align}
In the case of insulation materials, where the Knudsen number is often much smaller than 1, the thermal conductivity of the enclosed gas can be determined with the following formula [see M.G. Kaganer: “Thermal insulation in cryogenic engineering“, 1969]:
\begin{align}
\label{lam}
&\boxed{\lambda = \frac{\lambda_0}{1+2\beta \cdot Kn}} \\[5px]
\end{align}
In this formula, λ0 denotes the thermal conductivity under standard conditions (1 atm, 0°C) and β is a weighting factor which will not be discussed further here. Even if the use of equation (\ref{lam}) requires that the Knudsen number is much smaller than 1, it should still be as high as possible, especially for insulating materials! This then results in low thermal conductivity.
For low thermal conductivity, the Knudsen number should be kept as high as possible!






