In this article, learn more about the relationship between internal energy and heat capacity in connection with the kinetic theory of gases.
Internal energy
In the article equipartition theorem it has already been explained in detail that the energy of a gas is equally divided among the different microscopic forms of energy. In the case of monatomic ideal gases, this only includes the kinetic energy of the gas particles in terms of the translational motion (motion of the centre of gravity). In contrast to monatomic ideal gases, the molecules of polyatomic gases can also store energy in terms of a rotational motion. In addition, the atoms of gas molecules are connected to each other by “elastic” binding forces. Within certain limits, these binding forces can be considered analogous to an elastic spring. At the atomic level, vibrational energies are also found.

All the forms of energy mentioned above are present at the atomic level, i.e. “inside” the gas. The sum of these energies of each individual molecule thus contributes to the energy content of the entire gas. The energy content of the gas is also called internal energy. The particles represent so to speak “energy storages” for the internal energy.
Internal energy is the “atomic” energy content of a substance, which is contained in the kinetic energy of the particles, among other things!
In fact, other forms of energy are counted as internal energy as well, such as ionization energies or chemically bound energies, which can be released by chemical reactions. In comparison to these forms of energy it is characteristic for the translational, rotational and vibrational energy that these are related to random motions of the molecules. Therefore, these energies, which are related to the random motions of the particles, are referred to as thermal energy in the narrower sense. In this respect, the thermal energy of the random molecular motion is only a part of the internal energy.
Thermal energy refers to the energy stored in the random motion of the molecules (translation, rotation, vibration)!
In the context of the kinetic theory of gases, however, it is sufficient to reduce the internal energy to the thermal energy, since neither chemical reactions nor ionizations or the like are considered. When we talk about the internal energy in the following, we mean exclusively the thermal energy.
Degrees of freedom
The different types of thermal energy can even be further divided. For example, a molecule can move in three independent spatial directions. The translational energy can thus be divided among each direction, i.e. a kinetic energy related to the x-direction, the y-direction and the z-direction. For the rotation, a division of the rotational energy can take place analogously, which is then linked with a rotation around the x-axis, y-axis and z-axis. The same applies to the vibrational energy, which can occur in different ways with molecules. All these possibilities of energy storage are also called degrees of freedom.
In the thermodynamic sense, the term “degrees of freedom” refers to the possibilities of storing energy as translational, rotational and vibrational motion of a molecule!
Translational motion has a total of three degrees of freedom, namely for each spatial direction one (because translational kinetic energy can be stored in terms of the motion in each direction). The same applies to rotation, in which rotational energy can be stored around each of the three spatial axes. Thus, rotational motion also has three degrees of freedom.
In the case of diatomic molecules (or linear molecules in general, i.e. molecules whose atoms are all on a common axis) there is a peculiarity in the degrees of freedom of rotation. One would probably assume three degrees of freedom, since the molecule should be able to rotate both around the x-axis and the y-axis as well as around the z-axis (molecular axis).
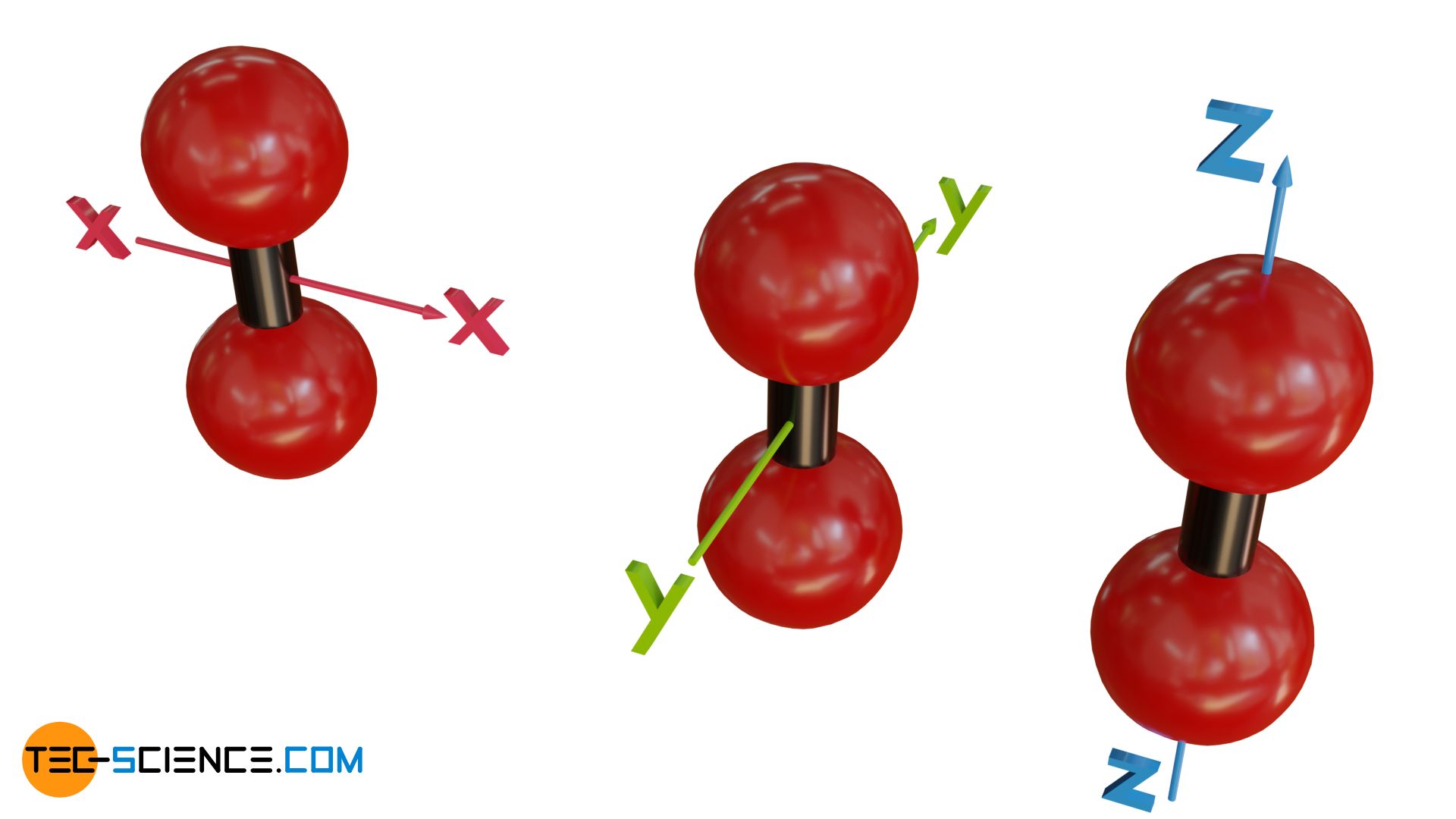
In fact, however, linear molecules will not rotate around their molecular axis and thus will not be able to use this degree of freedom for energy storage. This has to do with quantum effects. One can also clarify this fact by idealizing the gas as an ideal gas. If the atoms of a linear molecule are regarded as mass points, then, effectively speaking, there will be no mass in rotation when rotating around the molecular axis and thus no rotational energy (no moment of inertia, since the entire mass is concentrated in the center of rotation).
The missing degree of freedom of rotation around the molecular axis can also be explained by the fact that if the atoms are assumed to be rigid, friction-free spheres, there is no possibility to rotate them around the molecular axis. Because of the sphere-shape, each collision with other particles will be directed directly towards the molecular axis. Thus, no torque (no right-angled lever arm) is possible that could cause a linear molecule to rotate around the molecular axis. Therefore, this degree of freedom is omitted as energy storage for linear atoms.
Linear molecules have only two degrees of freedom for rotation!
In addition to the translational motion and rotational motion, molecules with two or more atoms can also vibrate. The possibilities of vibration (also called normal modes of vibration) depend on the number of atoms and the shape of the molecule. The atoms of diatomic molecules can only oscillate along their molecular axis and thus have only one vibrational degree of freedom (one normal mode of vibration).

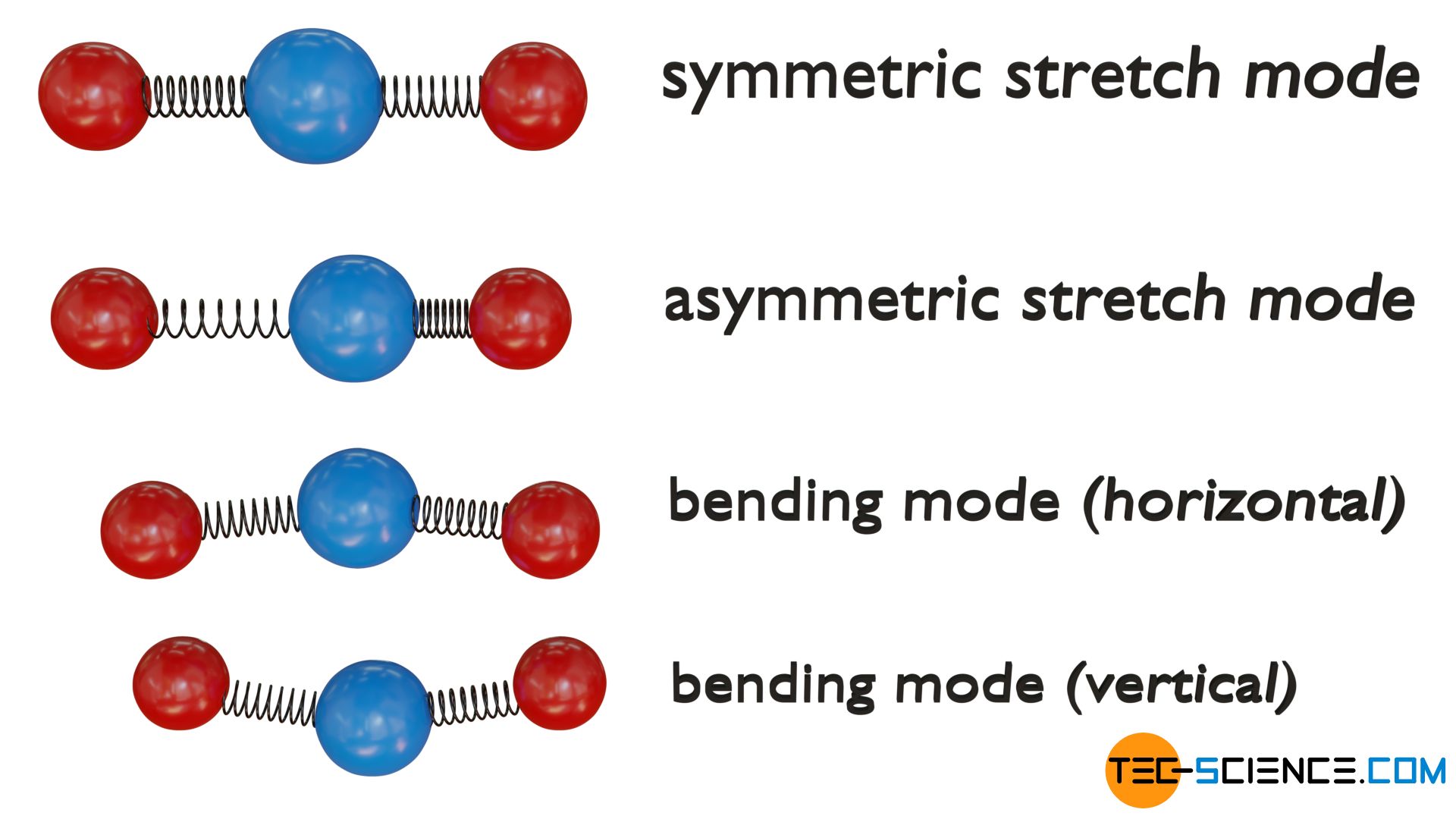
Triatomic linear molecules, on the other hand, have four vibrational degrees of freedom. The atoms can either vibrate symmetrically along their bond axes (symmetric stretch mode) or phase-shifted (asymmetric stretch mode). In addition, two bending modes are possible, each of which leads to a change in the bond angle. A distinction is made between vertical and horizontal vibration mode.
Triatomic non-linear molecules, however, have a total of three degrees of freedom of vibration. On the one hand again a symmetrical stretching vibration and on the other hand again a asymmetric stretch mode along their bond axes. In addition, a bending mode is present wihtin the molecular plane.
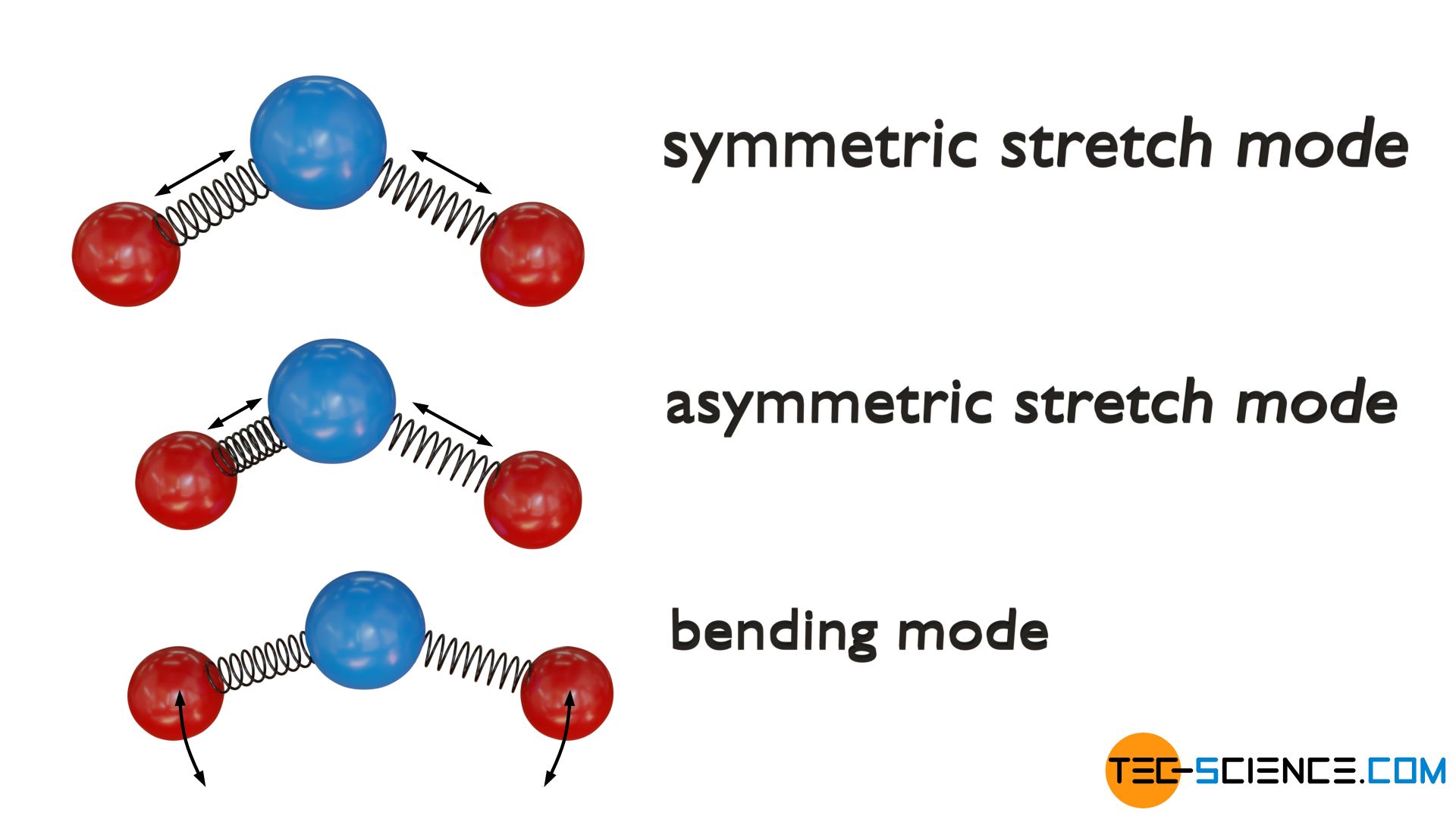
From an energetic point of view, however, it must be taken into account with all vibrational degrees of freedom that a vibration contains both kinetic energy and potential energy. The vibrational energy is “redistributed” during a period, i.e. potential energy is gradually converted into kinetic energy and vice versa; the energy sum as the actual vibrational energy, however, always remains constant. Thus a normal mode of vibration always has two possibilities to store energy. As kinetic energy and as potential energy. Therefore, from an energetic point of view, each degree of freedom of a vibrational motion must be counted twice!

From an energetic point of view, degrees of freedom of vibrational motions are counted twice, because a vibration contains both potential and kinetic energy!
The table below shows the number of degrees of freedom f for monatomic particles, diatomic molecules (linear molecules) and non-linear molecules, divided into the various forms of motion.
| Particle type | Translation ftrans | Rotation frot | Vibration fvib | Total f |
| monatomic | 3 | 0 | 0 (x 2) | 3 |
| diatomic (linear) | 3 | 2 | 1 (x 2) | 7 |
| triatomic (non-linear) | 3 | 3 | 3 (x 2) | 12 |
| triatomic (linear) | 3 | 2 | 4 (x 2) | 13 |
The total number of degrees of freedom f results from the sum of the individual degrees of freedom for translation (ftrans), rotation (frot) and vibration (fvib):
\begin{align}
&\boxed{f = f_{trans} + f_{rot} + 2 \cdot f_{vib}} \\[5px]
\end{align}
Equipartition theorem
There is a particular reason for such a division of energy into different degrees of freedom. Because it has been shown that the (internal) energy of a gas is equally divided among all degrees of freedom (see also main article equipartition theorem). The same amount of energy that, for example, is contained in the translational motion of the particles in the x-direction is also present as rotational energy of the particles around the z-axis. On average, this amount of energy will, for example, also be stored in the potential energy or kinetic energy of a vibrational motion.
Such a uniform distribution of the energy among the different degrees of freedom is also referred to as the equipartition theorem.
The equipartition theorem describes the equal division of the energy among the various degrees of freedom!
The article Pressure and Temperature shows that the temperature T of a gas is linked to the mean translational kinetic energy W of a particle by the following equation (with kB as the Boltzmann constant):
\begin{align}
\label{bew}
&W_{kin} = \frac{3}{2} k_BT ~~~~~\text{mean translational kinetic energy of a particle}\\[5px]
\end{align}
This relationship is at first only valid between the temperature and the energy that is in the (three-dimensional) translational motion of a particle. Each degree of freedom of the translational motion thus has an average energy of ½⋅kB⋅T according to the equipartition theorem.
However, the equipartition theorem is not limited to the translational kinetic energy, but applies to all forms of energy. If a degree of freedom of the translational motion has an average energy of ½⋅kB⋅T, then this also applies to the degrees of freedom of rotation and vibration (because the energy is just equally distributed among all degrees of freedom!).
On average, each degree of freedom (no matter if translational, rotational or vibrational!) has an energy of ½⋅kB⋅T. If one knows the total number of degrees of freedom f of a molecule, then this molecule carries on average an energy of W=f⋅½⋅kB⋅T at a given temperature T:
\begin{align}
\label{frei}
&\boxed{W = \frac{f}{2} k_BT~} ~~\text{energy of a molecule}\\[5px]
\end{align}
If, in addition, the number of molecules N in a gas is known, then the total energy of the gas and thus its internal energy can be determined. Because if a particle has on average an energy W, then the total energy U=N⋅W will be present in the gas:
\begin{align}
&\boxed{U = \frac{f}{2}Nk_BT~} ~~~~~\text{internal energy of an (ideal) gas}\\[5px]
\end{align}
The internal energy of the gas can be expressed not only by the number of molecules but also by the amount of substance n=N/NA, i.e. by the “number of moles” (with NA as Avogadro constant):
\begin{align}
&U = \frac{f}{2} \cdot n \cdot \underbrace{N_A \cdot k_B}_{R_m} \cdot T \\[5px]
\end{align}
In the equation above, the Avogadro constant NA and the Boltzmann constant kB can be combined to a new constant, the so-called molar gas constant Rm (also called universal gas constant or ideal gas constant):
\begin{align}
\label{inn}
&\boxed{U = \frac{f}{2} R_m n T~}~~~~~R_m = 8,314 \frac{\text{J}}{\text{mol}\cdot\text{K}} \\[5px]
\end{align}
Change of internal energy
The understanding of the degrees of freedom and the connection to the internal energy can now be used to calculate the temperature change of an ideal gas when energy in form of heat or mechanical work is supplied.
For this an ideal gas is considered whose degrees of freedom f are assumed to be known. If the internal energy of the gas changes by an amount ΔU, then this results in a temperature change ΔT, since all other values in equation (\ref{inn}) are constant:
\begin{align}
\label{du}
&\boxed{\Delta U = \frac{f}{2} R_m n ~ \Delta T~} ~~~~~\text{valid for any thermodynamic process of an ideal gas} \\[5px]
\end{align}
This fact also becomes clear. If, for example, the internal energy of a gas is increased by adding heat, the increase in energy will be equally divided among all forms of energy. Also the translational kinetic energy will increase, which is directly connected with a temperature increase according to the equation (\ref{bew}). Conversely, a reduction of the internal energy through heat dissipation will lead to a reduction of the kinetic energies and thus lower the temperature.
The temperature increase during a compression of a gas can also be explained with this equation. If a gas is compressed (by mechanical work), the required energy is used to increase the internal energy of the gas. According to the equation (\ref{du}), this is associated with an increase in temperature. This principle of increasing the temperature by compression is used, for example, in diesel engines to heat the fuel-air mixture so strongly that it ignites itself.
The animation below shows an experiment to demonstrate the temperature increase during compression. A piece of a cotton pad is placed in a plexiglass cylinder. The cylinder is closed with a piston. If the piston is then suddenly moved downwards, the air in it is compressed and heats up to such an extent that the cotton pad ignites.

The compression must therefore take place very quickly, otherwise the gas on the relatively cool cylinder walls would immediately cool down again. The rapid compression prevents heat dissipation from the gas (so-called adiabatic process).
The temperature increase during compression can also be explained in another way. If the piston is moved into the cylinder, then the piston collides with gas particles like a tennis racket with tennis balls. The speed of the molecules increases, which means an increase in temperature.
In practice, such a complex experimental setup is not required to demonstrate the temperature increase during compression. The daily experience of inflating a bicycle tyre already shows that air heats up during compression. The heating of the air pump is not due to friction as one might think but mainly to the energy input in terms of mechanical work during compression so that the gas heats up!
Molar heat capacity
The qualitative statements about the connection between an energy input – in particular a heat supply – and the resulting temperature increase will be discussed in more detail in the following.
Molar heat capacity of isochoric processes
If a gas is supplied with a certain amount of heat – and the gas itself does not release any energy by mechanical work or heat dissipation (!) – then the supplied heat completely benefits the internal energy of the gas (law of conservation of energy). The internal energy will therefore increase by the amount of the supplied heat Q, i.e. the heat supply Q corresponds directly to the change of the internal energy ΔU:
\begin{align}
& Q \overset{!}{=} \Delta U \\[5px]
&\boxed{Q = \frac{f}{2}R_m n \cdot \Delta T~} ~~~~~\text{only valid for isochoric processes of ideal gases} \\[5px]
\end{align}
This equation applies not only to a heat supply, but also to a heat dissipation (the heat then has a negative sign in the thermodynamic sense). As already explained, heat dissipation leads to a reduction of the internal energy and thus to a lowering of the temperature (negative temperature change).
What is remarkable about the above equation is that it obviously does not matter which type of gas exactly is involved. There is no gas-specific quantity in this equation. Of importance is only the number of degrees of freedom of the molecules, but not the type of atoms that make up the molecule. For an ideal gas, therefore, only the “shape” of the molecule is important, i.e. whether it is monatomic (f=3), diatomic or linear (f=7) or non-linear (f=12), as this determines the number of degrees of freedom (see table above).
The constant term f/2⋅Rm for a certain number of degrees of freedom is also known as the molar heat capacity Cm,v, because it determines the quantitative relationship between a heat input/output and the temperature change:
\begin{align}
\label{qv}
&\boxed{Q = C_{m,v} \cdot n \cdot \Delta T~} \\[5px]
\label{c}
&\boxed{C_{m,v} := \frac{f}{2}R_m} = \frac{Q}{n ~ \Delta T} ~~~~\left[C_{m,v}\right]=\frac{\text{J}}{\text{mol} \cdot \text{K}}\\[5px]
\end{align}
As can be seen from equation (\ref{c}), the molar heat capacity indicates how much heat must be added to increase the temperature of a gas with an amount of substance of one mole by one Kelvin.
The molar heat capacity indicates how much heat is required to heat one mole of a substance by one Kelvin!
Equation (\ref{qv}) was derived under the condition that the gas would not release any energy during the heat supply. The question then arises how such a thermodynamic process would look in practice.
A simple example is a sealed container filled with gas and heated with a Bunsen burner. Although the vessel absorbs a part of the supplied heat and the gas can release a part of the supplied heat to the environment through the vessel, the equation (\ref{qv}) remains valid if the heat Q is based on the net amount, i.e. the heat effectively supplied to the gas.

However, a gas can not only release energy into the environment in terms of heat but can also perform mechanical work. Think, for example, of a piston in a cylinder of a combustion engine, which is pushed downwards by the gas pressure with a certain force during this work cycle. The gas obviously releases energy in terms of mechanical work.
In principle, a gas will always perform mechanical work when its volume increases. This is because an increase in volume always means that the gas increases its volume along a distance with a certain force (caused by the gas pressure at the system boundary). After all, a force acting along a distance is precisely the definition of mechanical work. Therefore, a change in volume of a gas is always associated with mechanical work. In this context, one often speaks of a pressure-volume work.
Pressure-volume work (PV work) refers to the mechanical energy supplied to a gas during compression or the mechanical energy released by the gas during expansion!
For the equation (\ref{qv}) to be valid, the gas volume must therefore be kept constant during the heat supply, otherwise this equation loses its validity due to the mechanical work still to be taken into account (for this reason, the vessel considered is closed with a cork!). Such a type of heat supply under constant volume is also referred to as an isochoric process.
A thermodynamic change of state at a constant volume is also called an isochoric process!
To make it clear that equation (\ref{qv}) only applies to an isochoric process (and Q as net heat amount), the letter v is added to the molar heat capacity (“constant volume”). Note that with an isochoric process, the heat supplied is completely used to increase the internal energy, or the heat dissipated is completely at the expense of the internal energy (see energy flow diagram below).

Important note
With the definition of the molar heat capacity of the isochoric process Cm,v the change of the internal energy ΔU can also be expressed with this quantity [see equation (\ref{du})]:
\begin{align}
\label{du2}
&\boxed{\Delta U = C_{m,v} n ~ \Delta T~} ~~~~~\text{applies to any thermodynamic process of ideal gases} \\[5px]
\end{align}
In contrast to equation (\ref{qv}), equation (\ref{du2}) applies to any thermodynamic process of an ideal gas, even if it contains the molar heat capacity of the isochoric process! For the change of the internal energy the use of this quantity is only a purely formal way of writing!
Molar heat capacity of isobaric processes
During the considered isochoric heat supply of the closed vessel, the pressure will also increase as a result of the temperature increase. If, on the other hand, the cork is removed, the gas can expand under constant (ambient) pressure during the heat supply, i.e. increase its volume. In contrast to an isochoric process, a thermodynamic change of state under constant pressure is referred to as an isobaric process.
A thermodynamic change of state at constant pressure is also called an isobaric process!
Even for an isobaric process, a molar heat capacity can be defined as a function of the degrees of freedom. This will be shown in the following.
As an example of an isobaric process, a gas in a vertical cylinder is considered which is closed by a plate (“piston”) sliding frictionless in the cylinder. Under the weight of the plate, the gas is first compressed and the pressure increases until a state of equilibrium is reached.

In this state, the gas pressure p exerts the force Fp=p⋅A from inside the cylinder on the plate surface A. From the outside, the weight Fg=m⋅g acts on the plate surface (more precisely: on the interface to the gas, which is also called the system boundary) and the ambient pressure p0 as well (!), which additionally exerts a force F0=p0⋅A on the plate surface or on the system boundary.
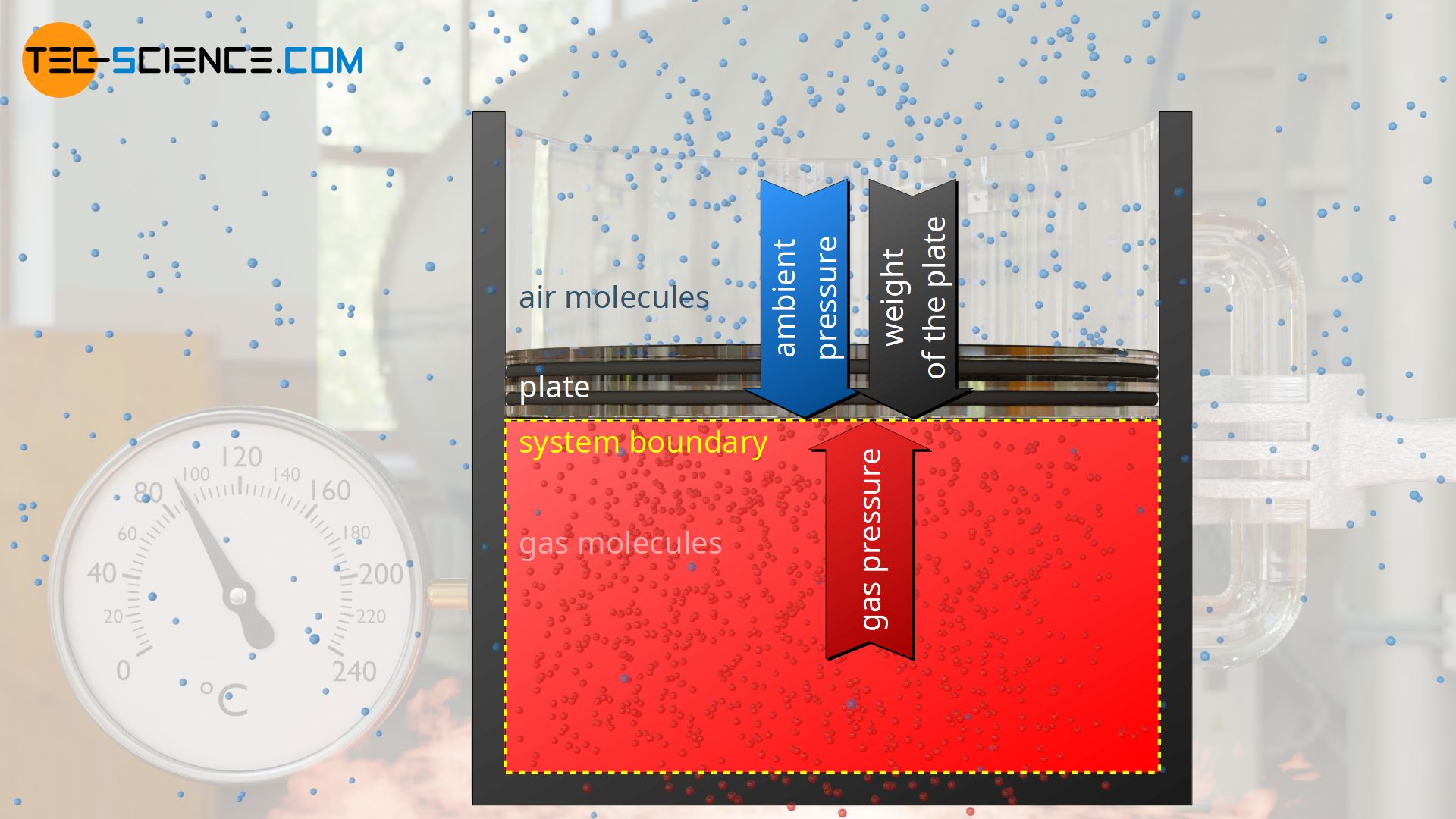
In the state of equilibrium, the external forces Fg and F0 are in equilibrium with the internal force caused by the gas Fp. The gas pressure p can be determined from this equilibrium analysis as follows:
\begin{align}
&F_p \overset{!}{=} F_g + F_0 \\[5px]
&p \cdot A = mg + p_0A\\[5px]
&\boxed{p = \frac{mg}{A}+p_0} \\[5px]
\end{align}
The gas pressure is obviously only influenced by mass of the plate (and its surface area) and by the ambient pressure. The weight of the plate and the ambient pressure forces the pressure of the gas. Even if the gas is now heated, this situation will not change in principle. The pressure will always be determined by the weight of the plate and by the ambient pressure (just imagine your hand being the gas; then you must apply the same force in each position to keep the plate in position against its weight and the ambient pressure). Thus one obtains a heat supply with which the pressure does not change!
One could also argue as follows: If the gas is heated, then a possible increase in pressure is compensated by a rising of the plate upwards (expansion), so that the pressure always remains constant.
From an energetic point of view, the gas is supplied with energy in terms heat on the one hand, while on the other hand the gas releases energy in terms of mechanical work by lifting the weight of the plate during expansion. The gas thus increases its internal energy by the amount of heat supplied Q and simultaneously reduces it by the amount of work done W, so that the internal energy effectively increases by the difference:
\begin{align}
\label{ees}
&\Delta U = Q – W \\[5px]
\end{align}

While the change of the internal energy is already given by equation (\ref{du}), the work done by the gas W can be determined from the constant force Fp=p⋅A with which the gas raises the plate by a distance Δh:
\begin{align}
&W = F_p \cdot \Delta h = p \cdot \underbrace{A \cdot \Delta h}_{\Delta V} = p \cdot \Delta V\\[5px]
&W = p \cdot \Delta V \\[5px]
\end{align}

In the equation above it was used that the product of the plates’s surface area A and lifting distance Δh corresponds to the change in volume ΔV of the gas. The work done as product of pressure and volume change can finally be expressed by the temperature change ΔT using the ideal gas law:
\begin{align}
&p V =R_m \cdot n \cdot T ~~~~~\text{ideal gas law} \\[5px]
&p \cdot \Delta V = R_m \cdot n \cdot \Delta T \\[5px]
\end{align}
The following relationship therefore applies between the work performed by the gas and the resulting temperature change of the gas:
\begin{align}
\label{w}
&W = p\cdot \Delta V= R_m \cdot n \cdot \Delta T \\[5px]
\end{align}
If the equations (\ref{du}) and (\ref{w}) are used in equation (\ref{ees}), the following relationship between the supplied heat and the resulting temperature change becomes apparent for an isobaric process:
\begin{align}
\Delta U &= Q – W \\[5px]
\frac{f}{2} R_m n ~ \Delta T &= Q – R_m \cdot n ~ \Delta T \\[5px]
Q &= \frac{f}{2} R_m n ~ \Delta T + R_m \cdot n ~ \Delta T \\[5px]
Q &= \underbrace{\left(\frac{f}{2} + 1\right)R_m}_{C_{m,p}} \cdot n ~ \Delta T \\[5px]
\end{align}
The expression marked above the underbrace can now be interpreted as the molar heat capacity of the isobaric process Cm,p, which describes the relationship between a heat supply at constant pressure and the resulting temperature change:
\begin{align}
\label{qp}
&\boxed{Q = C_{m,p} \cdot n \cdot \Delta T~} ~~~~~\text{and}~~~~~ \boxed{C_{m,p} := \left(\frac{f}{2}+1\right)R_m} \\[5px]
\end{align}
Relationship between the molar heat capacities
A closer look at the molar heat capacities shows that the molar heat capacity of the isobaric process is always greater by the value of the molar gas constant than the molar heat capacity for the isochoric process:
\begin{align}
\require{cancel}
& C_{m,p} – C_{m,v} = \left(\tfrac{f}{2}+1\right)R_m – \tfrac{f}{2}R_m = \bcancel{\tfrac{f}{2}R_m} + R_m – \bcancel{\tfrac{f}{2} R_m} = R_m \\[5px]
\label{cc}
&\boxed{C_{m,p} = C_{m,v} + R_m}
\end{align}
The always greater molar heat capacity Cm,p compared to Cm,v means that for an isobaric process obviously more heat has to be supplied in order to achieve the same change in temperature. This also becomes clear, because with an isobaric process the supplied heat is not completely used to increase the internal energy and thus the temperature, but a part of the heat is converted into mechanical work (note that a temperature change is directly linked to a change in the internal energy according to equation (\ref{du})!) However, if the same temperature change were to be caused, an amount of heat greater by the amount of work done by the gas would have to be added.

Adiabatic processes
Other important processes in thermodynamics are state changes that occur so quickly that in principle there is no time for heat supply or heat dissipation. Due to the high speeds in combustion engines, this is approximately the case, for example, with the expansion and compression processes that take place there. Such processes without heat transfer are also referred to as adiabatic processes. The experiment already described, in which a cotton pad was ignited by rapid compression of a gas, can be regarded as approximately adiabatic.
The heat capacity ratio plays an important role in describing these processes. This ratio is also called adiabatic exponent or isentropic exponent κ:
\begin{align}
\require{cancel}
& \kappa:=\frac{C_{m,p}}{C_{m,v}} = \frac{\left(\tfrac{f}{2}+1\right)\bcancel{R_m}}{\tfrac{f}{2}\bcancel{R_m}}= 1+ \frac{2}{f} \\[5px]
&\boxed{\kappa = 1 + \frac{2}{f}}
\end{align}
Molar heat capacities of selected gases
The table below shows the molar heat capacities and the isentropic exponents at room temperature for ideal gases and for selected real gases. It can be seen that helium comes very close to a monatomic ideal gas with three degrees of freedom. Similarly, nitrogen and air come very close to a diatomic ideal gas with seven degrees of freedom.
| Gas | Molar heat capacity of the isochoric process Cm,v [J/(mol⋅K)] | Molar heat capacity of the isobaric process Cm,p [J/(mol⋅K)] | Isentropic exponent κ |
| ideal, monatomic (f=3) | 12,5 | 20,8 | 1,67 |
| Helium He | 12,6 | 20,9 | 1,66 |
| Argon Ar | 12,4 | 20,7 | 1,67 |
| ideal, diatomic* (f=5) | 20,8 | 29,1 | 1,40 |
| hydrogen H2 | 20,2 | 28,6 | 1,42 |
| air | 20,7 | 29,1 | 1,41 |
| nitrogen N2 | 20,7 | 29,0 | 1,40 |
| oxygen O2 | 21,0 | 29,3 | 1,40 |
*) Important: diatomic gases can theoretically have 7 degrees of freedom, but in practice the two degrees of freedom of vibration are usually frozen at room temperature – more about this in the next section.
Note that in practice, the molar heat capacity is first determined from the temperature change at a given heat input according to equation (\ref{c}). Then the number of degrees of freedom can be deduced. Thus, it can be seen that the microscopic state in terms of the degrees of freedom of a gas can be inferred from macroscopically measurable quantities!
Dependence of molar heat capacities on temperature
If one considers the equations for determining the molar heat capacities, then these obviously depend only on the number of degrees of freedom:
\begin{align}
&C_{m,v} := \frac{f}{2}R_m \\[5px]
&C_{m,p} := \left(\tfrac{f}{2}+1\right)R_m \\[5px]
\end{align}
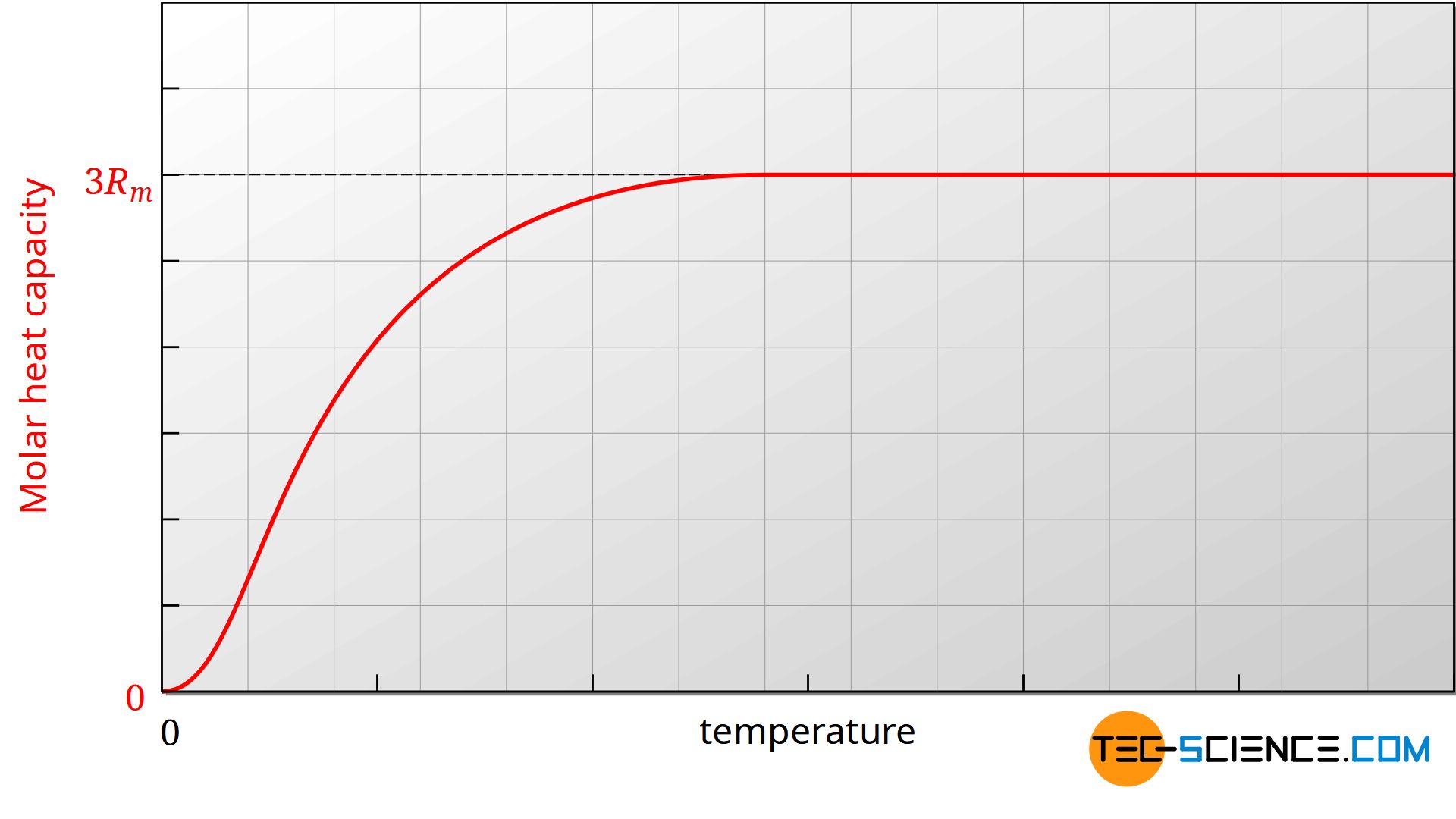
One could assume that the molar heat capacities are independent of the temperature. In practice, however, it is found that the heat capacities are largely constant only within certain temperature ranges. If, for example, the molar heat capacity Cm,v is plotted against the temperature in a diagram, then it can be seen that the molar heat capacity also decreases with decreasing temperature.
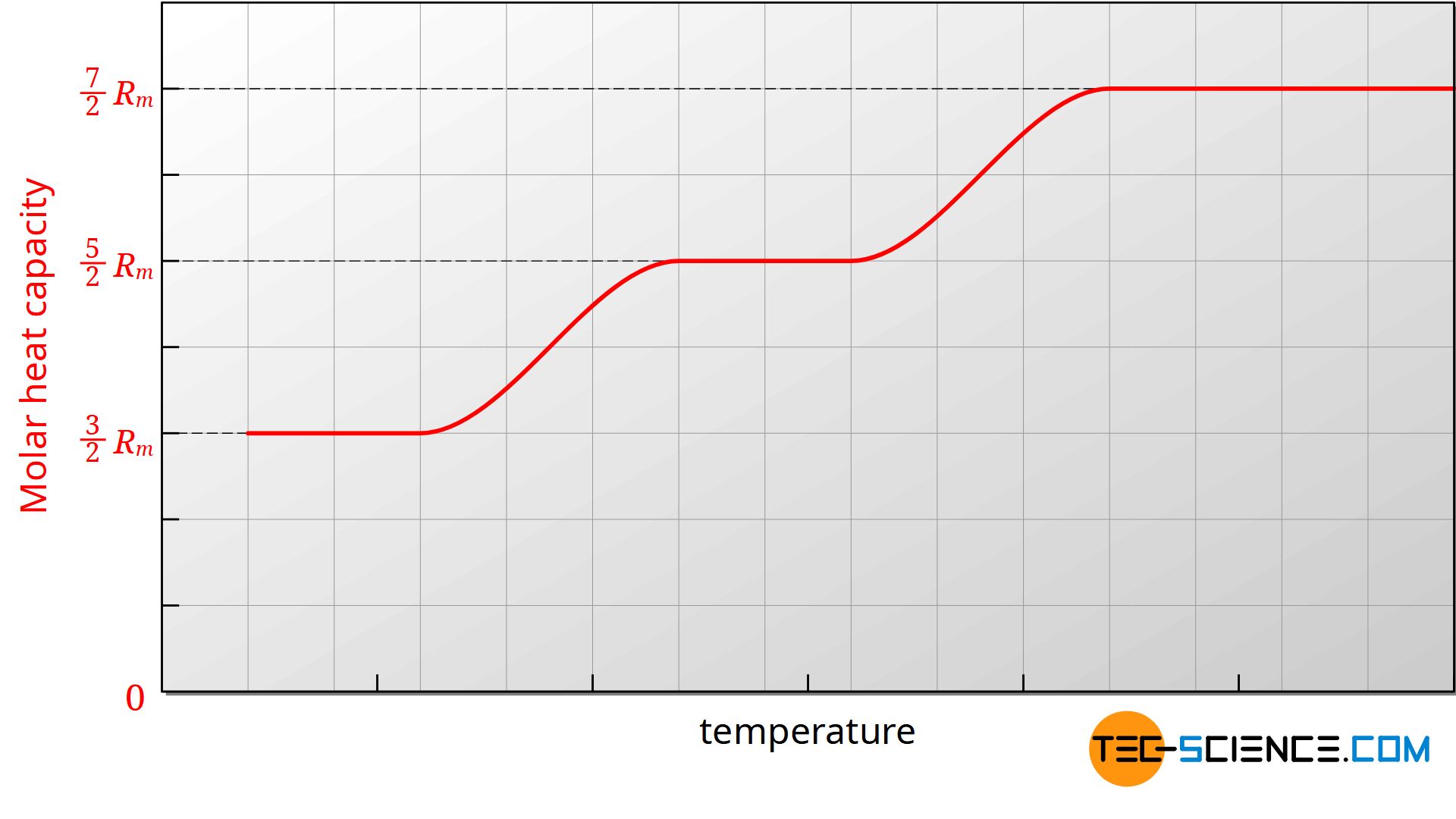
The figure above shows the course of the molar heat capacity of the isochoric process as a function of temperature (an ideal diatomic gas is assumed). Since the molar gas constant is a physical constant, the change in heat capacity must be due to the number of degrees of freedom. Obviously the number of degrees of freedom decreases with decreasing temperature.
The reduction of the degrees of freedom can only be explained by quantum mechanics, whose basic idea is based on the fact that energies cannot assume arbitrary values, but only discrete values. In order to excite a certain energy state of a molecule, certain minimum energies are necessary. For example, the oscillation of a diatomic molecule along its molecular axis requires a certain minimum energy. If this minimum energy is not present, then the vibration cannot be excited. If no vibration can be made possible, then this degree of freedom can not be used for energy storage. Due to insufficient energy of the molecules (equivalent to too low temperatures) this degree of freedom is so-called frozen.
A degree of freedom is called “frozen” if due to too low energy (i.e. too low temperature) this degree of freedom cannot be excited for quantum mechanical reasons and is therefore not present!
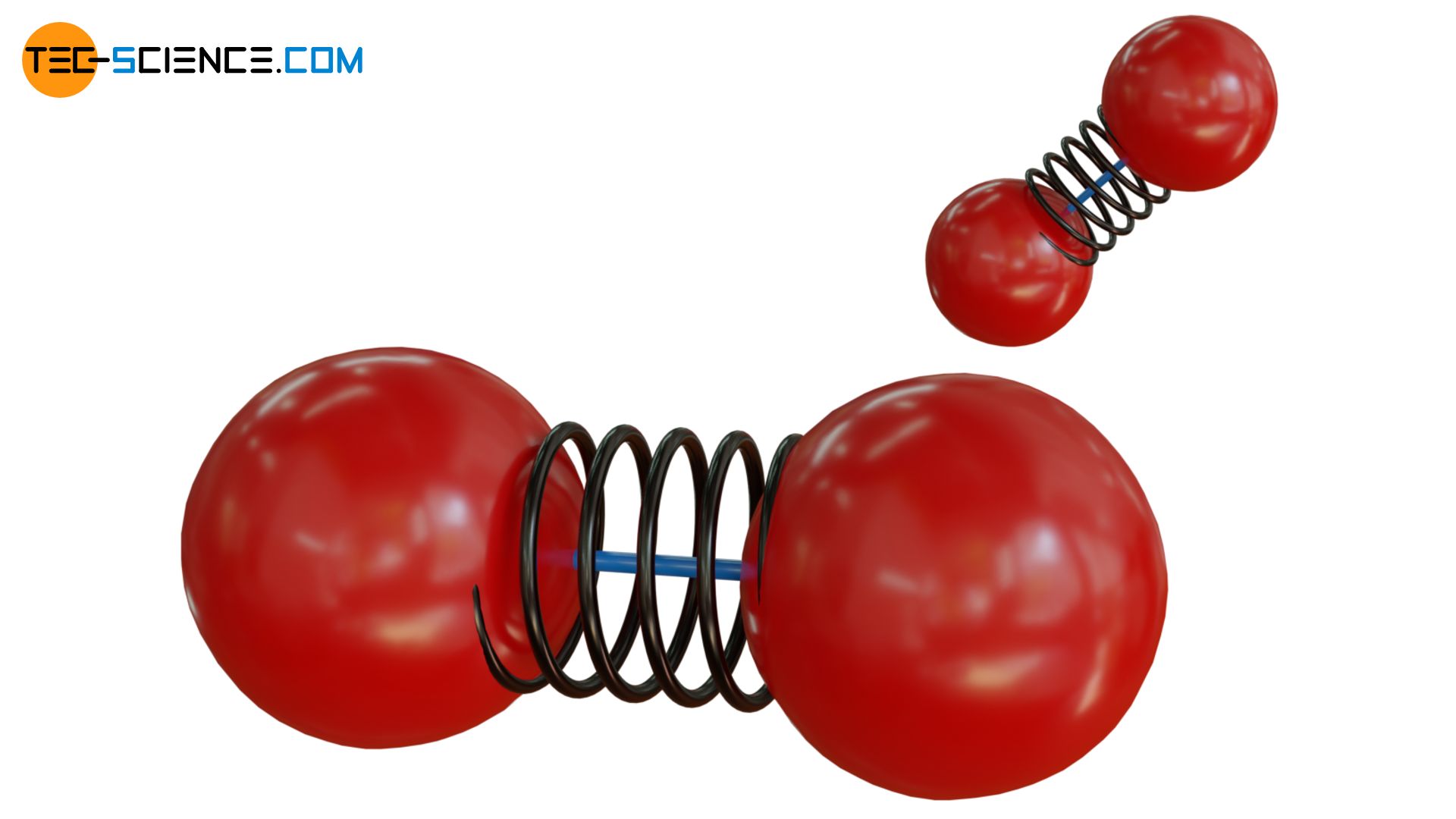
The situation can be illustrated with two balls (“atoms”) connected by an elastic spring (“binding forces”), but additionally by a fragile rod. At low kinetic energies, the rod will thus prevent the balls from vibrating. Thus, no energy can be stored in terms of vibrational energy. If, on the other hand, the kinetic energy is high (in the figurative sense this corresponds to a high temperature), then the rod can break in a collision with another particle. Now the balls are able to vibrate and can store vibrational energy accordingly.
The reason why the molar heat capacity drops within a temperature range and not suddenly is due to the characteristic speed distribution in an ideal gas. At a certain temperature, not all particles have the same speed. Some particles are slower and some faster. If the temperature drops, the degree of freedom is not frozen for all molecules at the same time, but only for those particles whose kinetic energies are too low.
With a diatomic gas, the degree of freedom of vibration is first frozen with decreasing temperature. Then the degree of freedom of rotation takes place.
Even if a gas is regarded as ideal, degrees of freedom are frozen in practice and the heat capacities change as a result. If such changes in the heat capacities are neglected for the sake of simplification, then one also speaks of perfect gases.
A perfect gas is an ideal gas whose heat capacities are regarded as constant, i.e. in particular no degrees of freedom are frozen with decreasing temperature!
Molar heat capacity of solids
A distinction between an isobaric and an isochoric process does not have to be made for liquids or solids in general. The reason for this is that solids and liquids are incompressible, i.e. they do not change their volume under pressure or with a change in temperature. The low thermal expansion is negligible! These substances are therefore not able to perform significant pressure-volume work. For this reason, a heat supply always resembles an isochoric change of state.
Empirical research has shown that in many cases the considerations about the degrees of freedom of ideal gases can also be applied to solids. In contrast to gases, molecules in solids cannot move freely but are bound to certain locations. In these cases, rotation of the molecules is also omitted. The movements of the molecules in solids are thus limited to vibrations around an equilibrium position, whereby the oscillations can take place in all three spatial directions.
For the molecules in solids there are three degrees of freedom of vibration, which have to be counted twice due to the potential and kinetic energy of an vibration. So with effectively six degrees of freedom there is a molar heat capacity for solids which theoretically corresponds to three times the molar gas constant:
\begin{align}
&C_{m} = \frac{f}{2}R_m = \frac{6}{2}R_m = 3 R_m \\[5px]
& \boxed{C_m = 25~\tfrac{\text{J}}{\text{mol}\cdot\text{K}} } ~~~~~\text{Dulong-Petit law} \\[5px]
\end{align}
And indeed, empirical research shows that this simple approach applies to many solids in good approximation. This connection is also known as the Dulong-Petit law. The term “law” is not really appropriate at this point, since it is rather an estimation.
The Dulong-Petite Law states that the molar heat capacity of solids is about three times the molar gas constant!
The table below shows the molar heat capacity at room temperature for selected solids. However, it can also be seen that the estimation according to the Dulong-Petite Law is a good approximation for many solids.
| Solid | Molar heat capacity Cm [J/(mol⋅K)] |
| Aluminium | 25 |
| Lead | 27 |
| Iron | 26 |
| Copper | 25 |
| Zinc | 25 |
| Tin | 26 |
Note that even in the case of solids with lower temperatures, more and more degrees of freedom are frozen. This is especially true in the vicinity of absolute zero, so that all degrees of freedom of vibration are frozen at this point at the latest. In principle, this applies to all substances, since no energy is present at absolute zero, but each degree of freedom in principle requires a certain minimum energy in order to be excited at all.
The heat capacity of substances decreases to zero as the temperature approaches absolute zero!
Specific heat capacity
As already explained, the molar heat capacity indicates how much heat has to be supplied to raise the temperature of a substance with one mole of particles by one Kelvin. If one wants to determine the temperature change of a substance with a heat supply, the amount of substance n must obviously be known:
\begin{align}
& Q = C_m n \Delta T \\[5px]
\end{align}
In practice, however, one usually does not measure the amount of substance, but the mass. Therefore, it is often usual to express the heat capacity not in relation to the amount of substance but in relation to the mass. The amount of substance and mass are connected by the molar mass. The molar mass M is defined as the quotient of the mass m and the amount of substance n and thus indicates how much mass per mole a substance has:
\begin{align}
& \boxed{M := \frac{m}{n}} \\[5px]
\label{n}
& n = \frac{m}{M} \\[5px]
\end{align}
If the amount of substance is expressed by the mass and the molar mass, then the following relationship between heat and temperature change applies:
\begin{align}
& Q = C_m \cdot \frac{m}{M} \cdot \Delta T = \underbrace{\frac{C_m}{M}}_{=c} \cdot m \cdot \Delta T =c \cdot m \cdot \Delta T \\[5px]
&\boxed{Q= c \cdot m \cdot \Delta T} \\[5px]
\end{align}
In the equation above, the quotient of molar heat capacity and molar mass (substance-dependent!) was combined to the specific heat capacity c:
\begin{align}
& \boxed{c = \frac{C_m}{M}}=\frac{Q}{m \cdot \Delta T} ~~~~~[c]=\frac{\text{J}}{\text{kg} \cdot \text{K} } \\[5px]
\end{align}
The specific heat capacity is a substance-specific quantity and indicates how much heat is needed to raise the temperature of a substance with a mass of one kilogram by one Kelvin!
The specific heat capacity of gases must also be differentiated between an isochoric and an isobaric heat supply. Accordingly, a distinction is made between the specific heat capacity of the isochoric process cv and the specific heat capacity of the isobaric process cp.
The relationship between the molar heat capacities Cm,v and Cm,p according to the equation (\ref{cc}) can now be used to create a relationship between the corresponding specific heat capacities:
\begin{align}
&C_{m,p} = C_{m,v} + R_m \\[5px]
&\frac{C_{m,p}}{M} = \frac{C_{m,v}}{M} + \underbrace{\frac{R_m}{M}}_{=R_s} \\[5px]
&\boxed{c_p=c_v+R_s} \\[5px]
\end{align}
The substance-dependent quotient of the molar gas constant Rm and the molar mass is combined to the so-called specific gas constant Rs:
\begin{align}
&\boxed{R_s=\frac{R_m}{M}} \\[5px]
\end{align}
Instead of using the molar heat capacity Cm,v to calculate the change in internal energy, the specific heat capacity cv can now also be used:
\begin{align}
&\boxed{\Delta U = c_{v} m ~ \Delta T~} \\[5px]
\end{align}