Die Wärmeleitfähigkeit von idealen Gasen ist für nicht allzu stark verdünnte Gase nicht vom Druck abhängig. Für verdünnte Gase gilt dies nicht mehr.
Einleitung
Im Artikel Wärmeleitung in Feststoffen und idealen Gasen wurde unter vereinfachter Betrachtung folgende Formel zur Abschätzung der Wärmeleitfähigkeit λ von idealen Gasen hergeleitet:
\begin{align}
\label{l}
& \boxed{\lambda = \frac{1}{3} \cdot c_v \cdot \rho \cdot v \cdot l} \\[5px]
\end{align}
Darin bezeichnet cv die spezifische Wärmekapazität bei konstantem Volumen, ϱ die Dichte des Gases, v die mittlere Geschwindigkeit der Gasmoleküle und l die mittlere freie Weglänge. Diese Formel soll im Folgenden näher betrachtet und die sich hieraus ergebenden Folgerungen für Gase diskutiert werden.
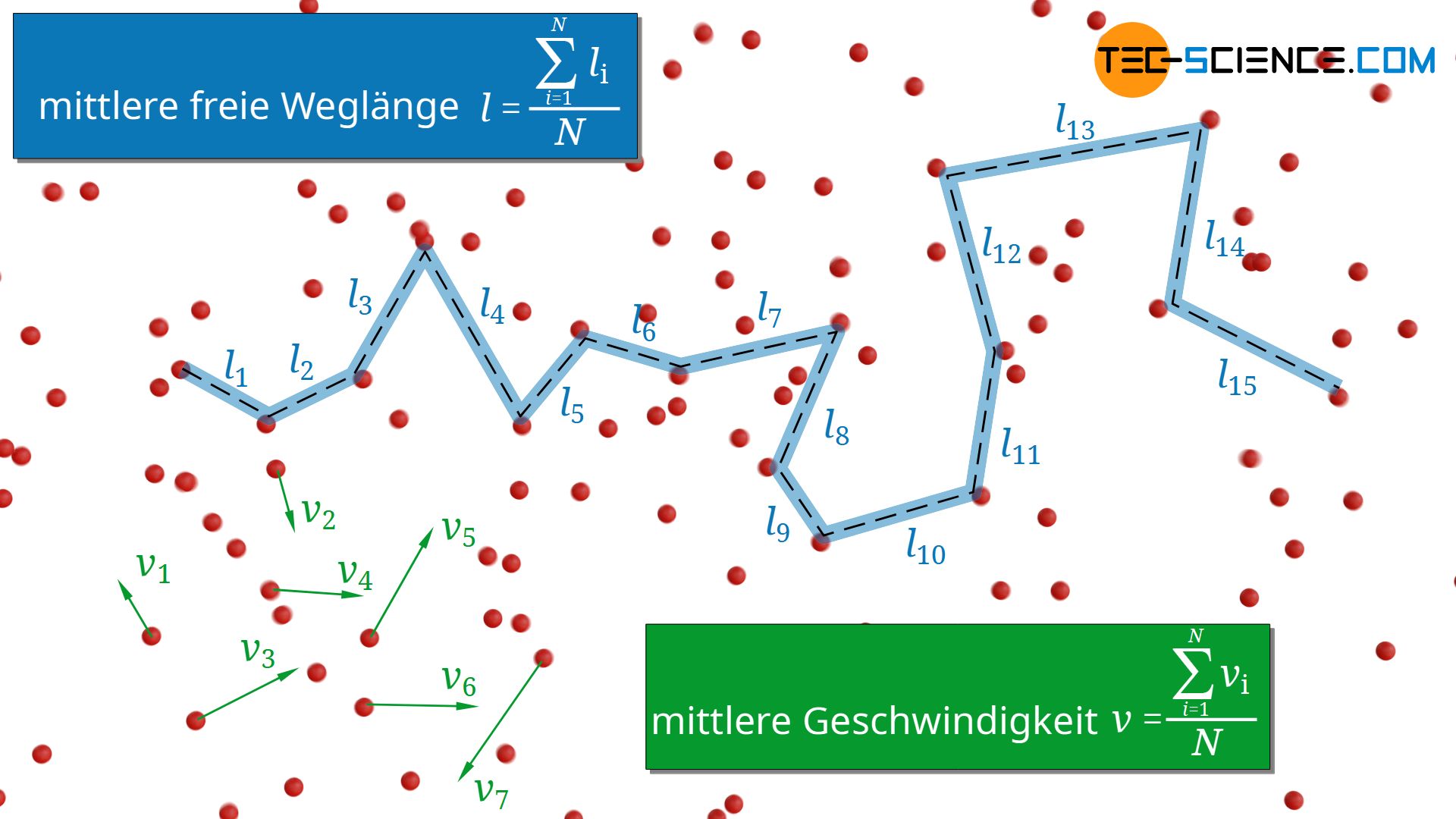
Anhand der Formel könnte man zunächst annehmen, dass die Wärmeleitfähigkeit vom Druck abhängig ist, denn umso größer der Druck, desto höher die Dichte des Gases. Diese Argumentation lässt sich auch mit Hilfe des Teilchenmodells anschaulich nachvollziehen, denn je mehr Teilchen vorhanden sind, desto mehr Energie können die Teilchen schließlich auch insgesamt transportieren. Beachte, dass gemäß der kinetischen Gastheorie nämlich jedes Gasteilchen pro Freiheitsgrad die Energie ½⋅kB⋅T (mit kB als Boltzmann-Konstante).
Im selben Maße wie die Dichte bei steigendem Druck allerdings zunimmt, nimmt die mittlere freie Weglänge ab! Tatsächlich ist die Wärmeleitfähigkeit von idealen Gasen somit unabhängig des Drucks oder der Teilchendichte (zur Einschränkung dieser Aussage, später mehr)!
Die Wärmeleitfähigkeit ist bei nicht allzu stark verdünnten Gasen nicht vom Druck abhängig!

Unabhängigkeit der Wärmeleitfähigkeit vom Druck für dichte Gase
Man kann die Unabhängigkeit der Wärmeleitfähigkeit vom Druck auch mathematisch zeigen. Hierzu wird die Dichte ϱ in Gleichung (\ref{l}) zunächst durch den Quotienten aus Gasmasse mgas und Gasvolumen Vgas ausgedrückt. Anschließend kann die Gasmasse durch die Stoffmenge ngas und die molare Masse Mgas des Gases ausgedrückt werden.
\begin{align}
\lambda &= \frac{1}{3} \cdot c_v \cdot \frac{m_{gas}}{V_{gas}} \cdot v \cdot l \\[5px]
&= \frac{1}{3} \cdot c_v \cdot \frac{n_{gas} \cdot M_{gas}}{V} \cdot v \cdot l \\[5px]
\end{align}
Das Produkt aus massen-spezifischer Wärmekapazität und molarer Masse, kann nun zur sogenannten molaren Wärmekapazität Cm,v zusammengefasst werden, wobei diese gemäß der kinetischen Gastheorie nur von der Anzahl der Freiheitsgrade f des Gases und der molaren Gaskonstante Rm abhängig ist (Cm,v=f/2⋅Rm). Zudem kann die Stoffmenge ngas durch das Verhältnis von Teilchenanzahl N und Avogadro-Konstante NA ausgedrückt werden (ngas=N/NA), sodass ferner gilt:
\begin{align}
\lambda &= \frac{1}{3} \cdot \underbrace{c_v \cdot M_{gas}}_{C_{m,v}} \cdot \frac{n_{gas}}{V} \cdot v \cdot l \\[5px]
& = \frac{1}{3} \cdot \underbrace {C_{m,v}}_{=\frac{f}{2}R_m} \cdot \frac{N}{N_A \cdot V} \cdot v \cdot l \\[5px]
& = \frac{1}{3} \cdot \frac{f}{2} R_{m} \cdot \frac{1}{N_A} \cdot \frac{N}{V} \cdot v \cdot l \\[5px]
& = \frac{f}{6} \frac{R_m}{N_A} \cdot \frac{N}{V} \cdot v \cdot l \\[5px]
\end{align}
Das Verhältnis von Teilchenanzahl und Gasvolumen entspricht der Teilchendichte n und der Quotient von molarer Gaskonstante und Avogadro-Konstante entspricht gerade der Boltzmann-Konstante kB (siehe Artikel Innere Energie & Wärmekapazität):
\begin{align}
\lambda & = \frac{f}{6} \underbrace{\frac{R_m}{N_A}}_{k_B} \cdot \underbrace{\frac{N}{V}}_{n} \cdot v \cdot l \\[5px]
\label{ll}
& = \frac{f}{6} k_B \cdot n \cdot v \cdot l \\[5px]
\end{align}
Nun fehlen noch die Zusammenhänge der mittleren Geschwindigkeit und der mittleren freien Weglänge. Die mittlere Geschwindigkeit v der Gasteilchen ist gemäß der Maxwell-Boltzmann-Verteilung wie folgt von der Temperatur T des Gases und der Masse m eines Gasteilchens abhängig (m bezeichnet darin die Masse eines einzelnen Gasteilchens und nicht die gesamte Gasmasse!):
\begin{align}
& \boxed{v = \sqrt{\frac{8 k_B T}{\pi m}}} \\[5px]
\end{align}
Die mittlere freie Weglänge l der Gasteilchen ist nicht nur von der Teilchendichte n abhängig, sondern auch vom Teilchendurchmesser d und lässt sich wie folgt bestimmen:
\begin{align}
& \boxed{l= \frac{1}{\sqrt{2} n \pi d^2}} \\[5px]
\end{align}
Werden beide Formeln in Gleichung (\ref{ll}) eingesetzt dann folgt für die Wärmeleitfähigkeit:
\begin{align}
& \lambda = \frac{f}{6} k_B \cdot n \cdot v \cdot l \\[5px]
& \lambda = \frac{f}{6} k_B \cdot n \cdot \sqrt{\frac{8 k_B T}{\pi m}} \cdot \frac{1}{\sqrt{2} n \pi d^2} \\[5px]
\require{cancel}
& \lambda = \frac{f}{6} k_B \cdot \cancel{n} \cdot \sqrt{\frac{8 k_B T}{\pi m}} \cdot \frac{1}{\sqrt{2} \cancel{n} \pi d^2} \\[5px]
& \lambda = \frac{f}{6} k_B \cdot \sqrt{\frac{8 k_B T}{\pi m}} \cdot \frac{1}{\sqrt{2} \pi d^2} \\[5px]
& \boxed{\lambda = \frac{f}{3d^2} \sqrt{\frac{k_B^3 T}{\pi^3 m }}} \\[5px]
\end{align}
Diese Formel zeigt nun deutlich, dass die Wärmeleitfähigkeit von idealen Gasen nicht von der Teilchendichte und damit nicht vom Druck abhängig ist. Zudem zeigt sich, dass Gase mit relativ großen Molekülen geringere Wärmeleitkoeffizienten aufweisen als Gas mit kleineren Molekülen (dies ist der Abnahme der mittlere freien Weglänge geschuldet, welche aus dem größeren Stoßdurchmesser d resultiert). Ferner gilt, dass die Wärmeleitfähigkeit für Gase mit leichten Teilchen größer ist als für Gase mit schwereren Teilchen. Zudem hängt die Wärmeleitfähigkeit von der Temperatur ab. Die Wärmeleitfähigkeit steigt mit zunehmender Temperatur!
Die Wärmeleitfähigkeit von Gasen ist umso größer, je kleiner und leichter die Gasteilchen sind und umso höher die Temperatur ist!
Abhängigkeit der Wärmeleitfähigkeit vom Druck bei stark verdünnten Gasen
Wenn der Druck keinen Einfluss auf die Wärmeleitfähigkeit bei Gasen hat, warum nutzt man dann ein Vakuum zur Wärmedämmung?
Dass die Wärmeleitfähigkeit nicht vom Druck abhängt, gilt nur solange die mittlere freie Weglänge sehr viel kleiner als das Volumen ist, in dem sich das Gas befindet. Verringert man in einem Gefäß den Druck bzw. die Teilchendichte mehr und mehr, dann stoßen die Teilchen nicht mehr untereinander zusammen, sondern davor mit den Gefäßwänden. Bei sehr geringen Drücken ist also die mittlere freie Weglänge durch die Dimension des Gefäßes bestimmt und nicht mehr durch den freien Weg zwischen zwei Teilchenstößen.
Dies gilt auch, wenn zwar nicht der Druck verringert wird, dafür aber die Gefäßdimension. Relevant wird dies bspw. bei Dämmstoffen, wo in kleinen Poren Gase eingeschlossen sind. Auch bei dünnen Folienschichten oder kleinen Spalten können sich solche Situationen ergeben, wenn sich dazwischen ein Gas befindet.
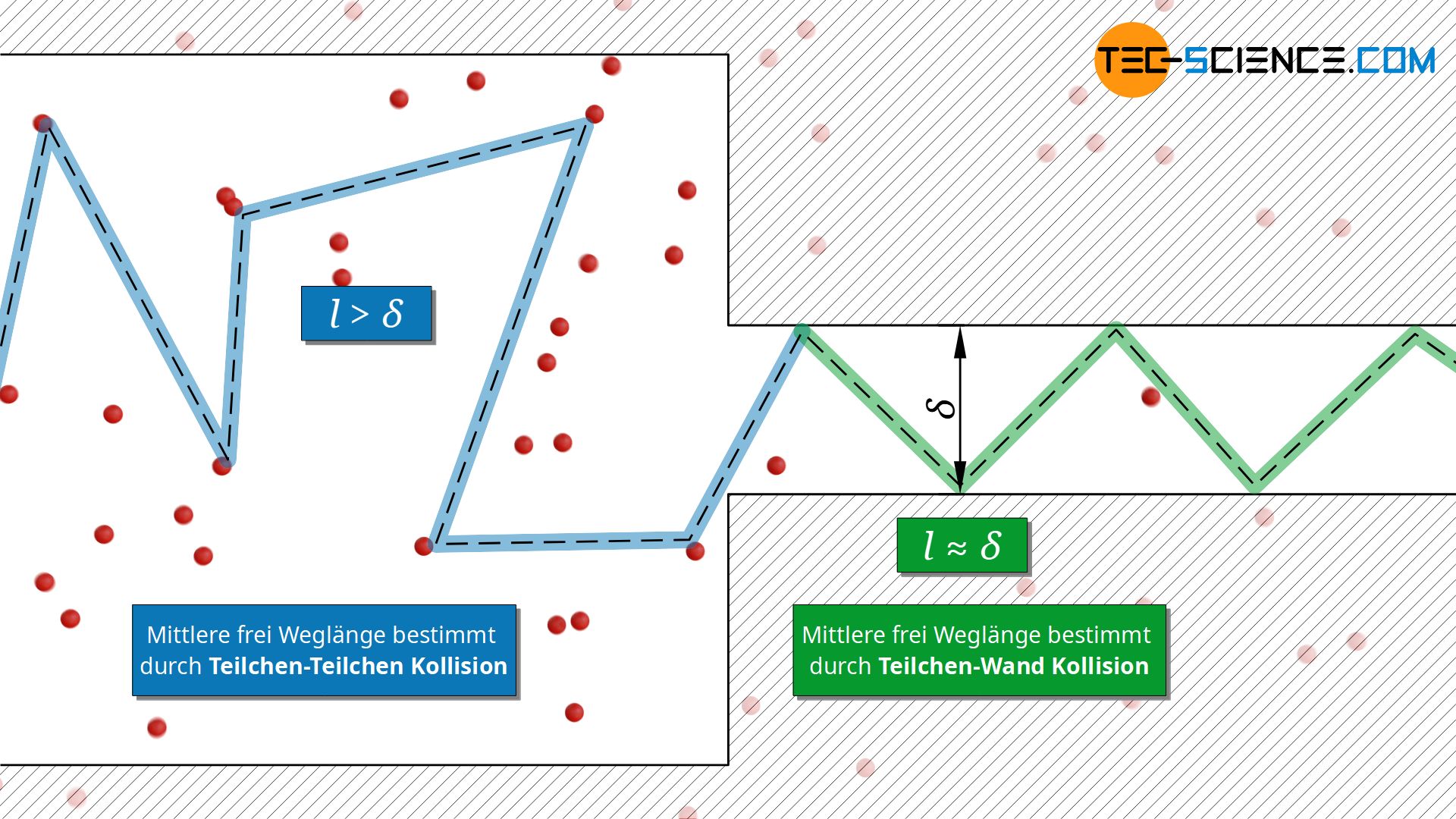
Die mittlere freie Weglänge entspricht in diesen Fällen der Abmessung δ des Volumens (z.B. Porenduchmesser oder Spaltabstand) und ist somit eine konstante Größe. In diesem Fall ist die mittlere freie Weglänge also nicht mehr von der Teilchendichte abhängig, sondern es gilt: l≈δ=konstant. Mit der mittleren freien Weglänge als Konstante, besagt Gleichung (\ref{ll}) dann eine Verringerung der Wärmeleitfähigkeit mit geringer werdender Teilchendichte!
\begin{align}
\label{a}
&\lambda = \frac{f}{6} k_B \cdot n \cdot v \cdot \delta \\[5px]
\end{align}
In stark verdünnten Gasen oder bei geringen Gasvolumina ist die Wärmeleitfähigkeit vom Druck abhängig!
In sogenannten Pirani-Vakuummetern nutzt man diesen den Zusammenhang, um anhand der Wärmeleitfähigkeit auf die Drücke in einem im Hochvakuum zu schließen.
Knudsen-Zahl
Wie bereits angedeutet, ist bei Materialien in der Dämmtechnik die charakteristische Länge δ der Poren oder der Folienabstand häufig sehr viel kleiner als die mittlere freie Weglänge l der darin eingeschlossenen Gase. In diesem Fall kann das Gas nicht mehr als Kontinuum beschrieben werden, sodass auch Gleichung (\ref{a}) in dieser Form nicht mehr angewendet werden kann (die qualitative Aussage dieser Gleichung verlieren aber nicht an Gültigkeit).
Als charakteristische Länge bezeichnet man die Abmessung/Größenordnung eines Systems!
Die sogenannte Knudsen-Zahl gibt in diesem Zusammenhang Aufschluss darauf, ob das Gas weiterhin als Kontinuum angesehen werden kann oder eben die Kinetik der Gastheorie angewendet werden muss. Die einheitenlose Knudsen-Zahl Kn beschreibt das Verhältnis der mittleren freien Weglänge l zur charakteristischen Länge δ des Gasvolumens:
\begin{align}
&\boxed{Kn := \frac{l}{\delta}} \\[5px]
\end{align}
Bei Werten sehr viel kleiner als 1 gilt weiterhin die Kontinuumsmechanik und bei Werten sehr viel größer 1 die Beschreibung mit Hilfe der Gesetze der kinetischen Gastheorie.
Da für ideale Gase die mittlere freie Weglänge nicht nur durch die Teilchendichte, sondern mit Hilfe der idealen Gasgleichung auch durch den Druck p ausgedrückt werden kann (siehe Artikel hier), lässt sich die Knudsen-Zahl wie folgt anhand des Drucks und der Temperatur ermitteln (d beschreibt den Durchmesser der Gasteilchen):
\begin{align}
&\boxed{Kn = \frac{k_B \cdot T}{\sqrt{2}\pi \cdot d^2 \cdot p \cdot \delta}} \\[5px]
\end{align}
Für den angesprochen Fall von Dämmstoffen, wo die Knudsenzahl häufig sehr viel kleiner 1 ist, kann die Wärmeleitfähigkeit des eingeschlossenen Gases nach M.G. Kaganer (Thermal insulation in cryogenic engineering, 1969) wie folgt ermittelt werden:
\begin{align}
\label{lam}
&\boxed{\lambda = \frac{\lambda_0}{1+2\beta \cdot Kn}} \\[5px]
\end{align}
Darin bezeichnet λ0 die Wärmeleitfähigkeit unter Normbedingungen (1 bar, 0°C) und β einen Gewichtungsfaktor, auf den an dieser Stelle nicht weiter eingegangen werden soll. Auch wenn zur Anwendung von Gleichung (\ref{lam}) die Voraussetzung gilt, dass die Knudsen-Zahl sehr viel kleiner 1 ist, sollte diese gerade für Dämmstoffe dennoch so hoch wie möglich sein! Hieraus resultiert dann eine geringe Wärmeleitfähigkeit.
Für eine geringe Wärmeleitfähigkeit sollte die Knudsen-Zahl möglichst groß gewählt werden!