The thermal conductivity in crystalline, non-metallic solids first increases and then decreases again with increasing temperature.
Phonons: Quasiparticles of the lattice vibrations
Thermal conduction refers to the transfer of thermal energy through a material. In gases and liquids, the energy-transferring particles are those particles that can move freely. In this way, energy is transferred from one particle to another by collisions. But how does this look like in solids? In metallic solids there are actually also such free particles. These are the free conduction electrons of the electron gas, which are mainly responsible for the good thermal conductivity.
In non-metallic solids, there are no real free particles, but the molecules are elastically bound to each other by binding forces. Heat transfer in such cases can be regarded as a transfer of vibrational energy from one particle to the next.
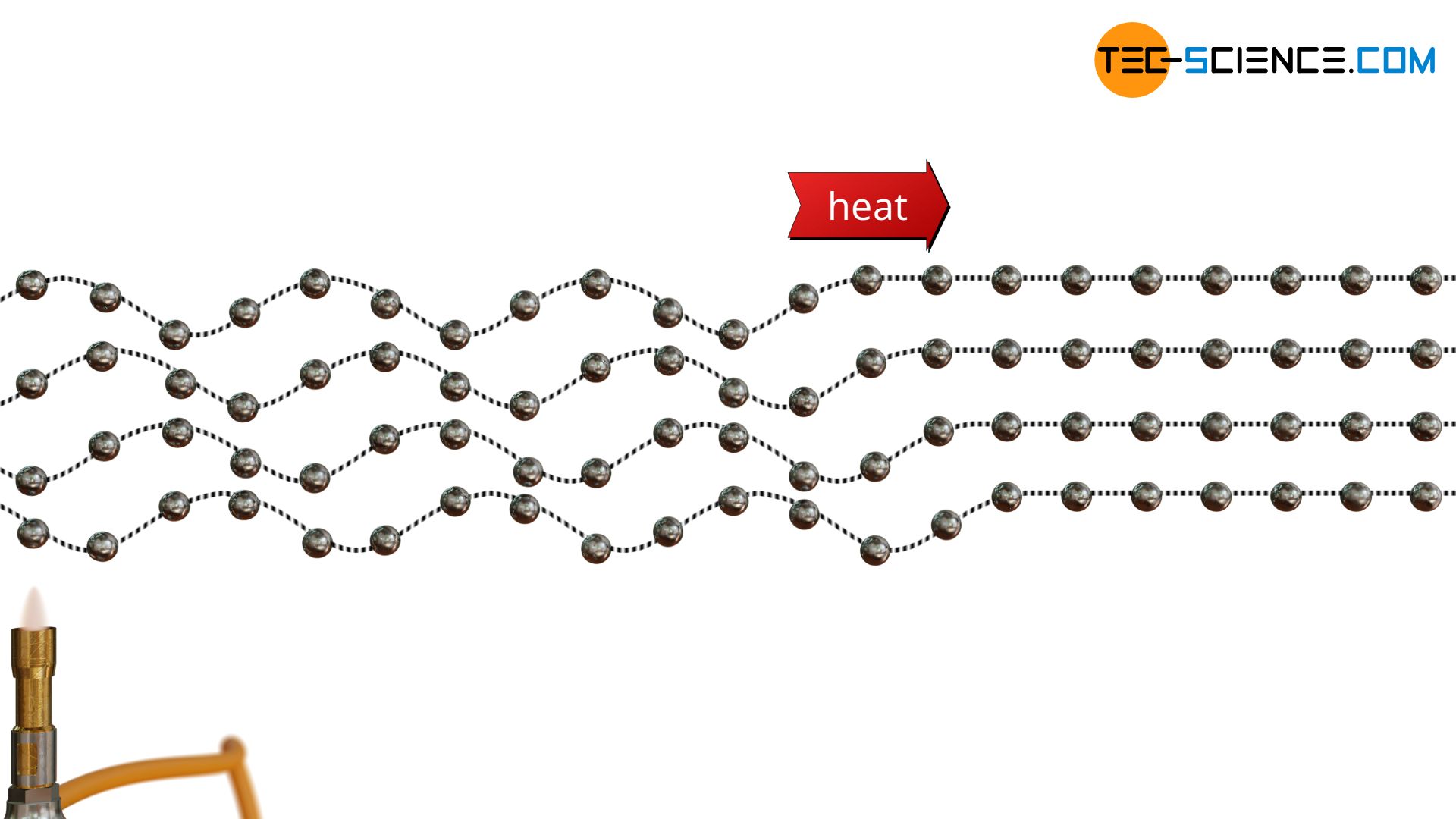
From quantum physics we know that each wave can be assigned a certain momentum (see mater wave). This momentum behaves in principle like the momentum of an imaginary particle. These quasi-particles, which are ultimately lattice vibrational waves, are also called phonons. The lattice vibration and thus the phonons are ultimately generated continuously at the heat source and move through the material. Just as thermal radiation is described by photons, heat conduction is described by phonons.
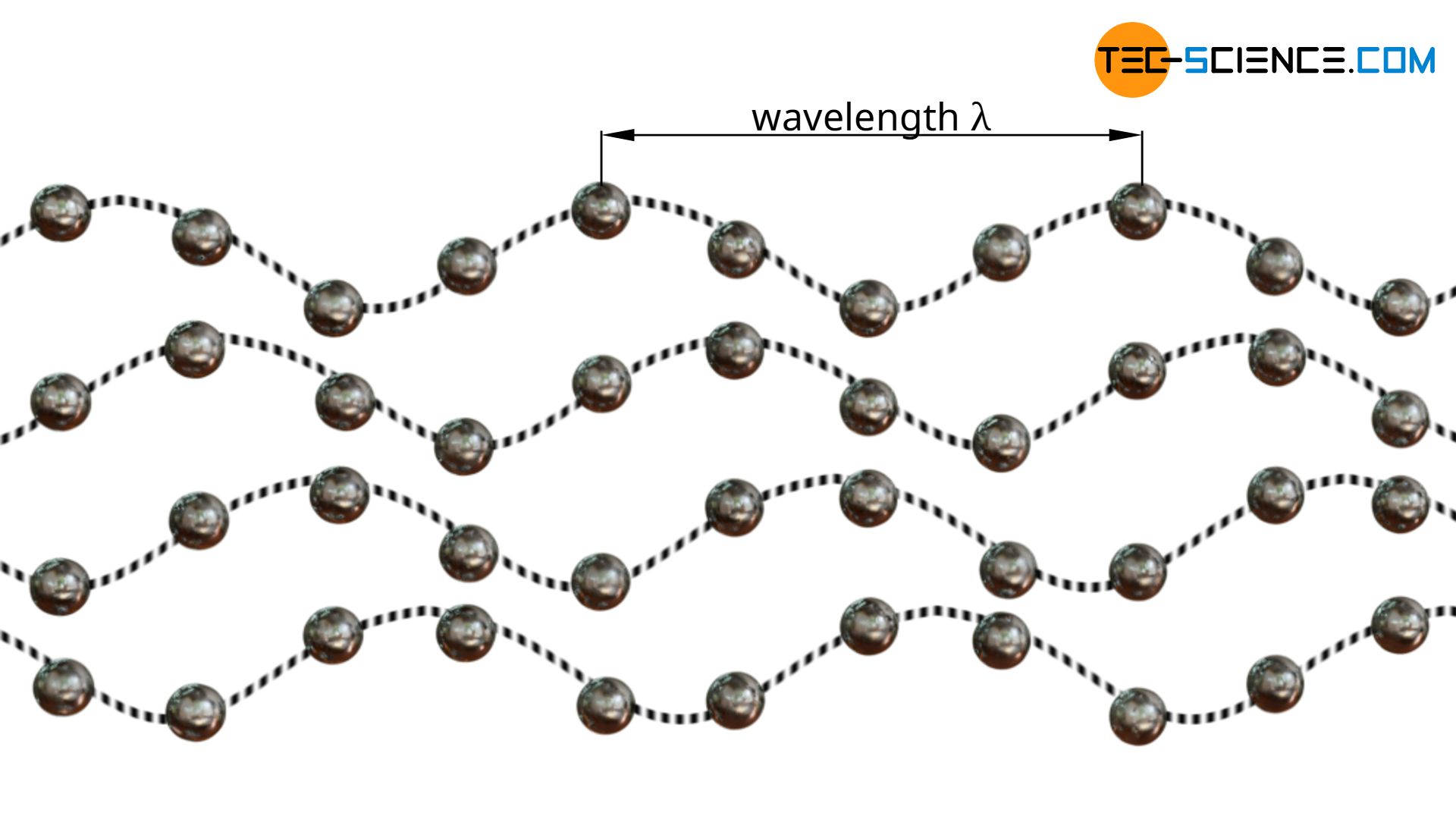
In the same way that photons represent the quasi-particles of an electromagnetic wave, phonons represent the quasi-particles of a matter wave (lattice vibrational wave).
Therefore, the transport of vibrational energy in non-metallic solids can also be understood as a migration of particles: the migration of phonons (energy quanta). In this way, the thermal conduction in gases, liquids and solids can be described as an energy transfer of colliding particles (energy diffusion).
Thermal conductivity in metals
By the way, in metals not only the electrons of the electron gas are involved in thermal conduction, but also the vibrating lattice structure, i.e. the phonons! Both together therefore make metals in general very good heat conductors. In the article Thermal conductivity some values for the thermal conductivity of selected materials are given.
Derivation of the thermal conductivity of non-metallic solids
Thermal conductivity
For a heat-conducting material with the thermal conductivity λ, the rate of heat flow Q* passing through the area A is determined by the temperature gradient present there, i.e. by the temperature drop ΔT along the distance Δx (Fourier’s law):
\begin{align}
& \boxed{\dot Q = \lambda \cdot A \cdot \frac{\Delta T}{\Delta x}} ~~~\text{Fourier’s law} \\[5px]
\label{q}
& \lambda = \frac{\dot Q \cdot \Delta x}{A \cdot \Delta T} \\[5px]
\end{align}
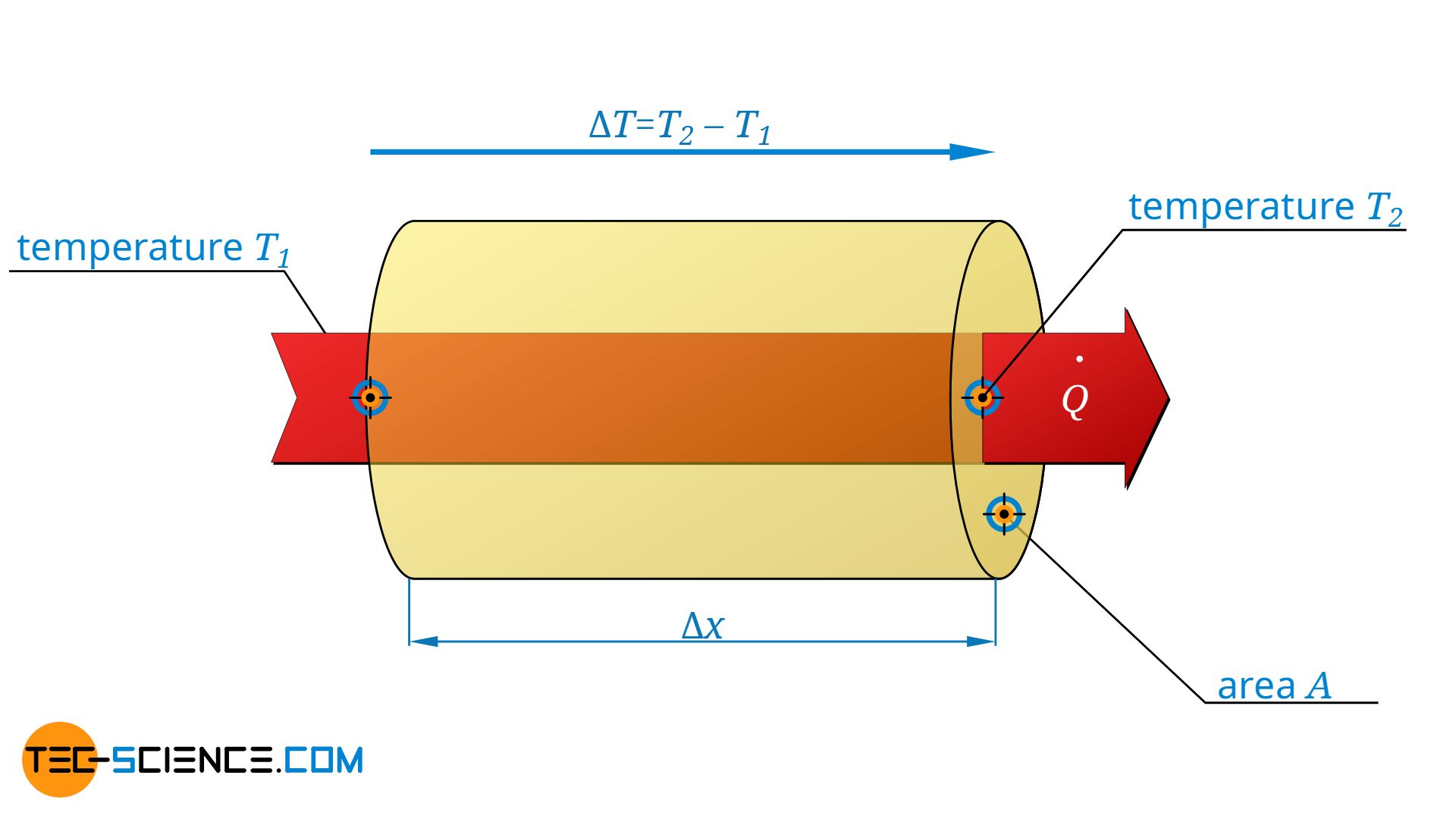
Note: For the sake of simplicity, the negative sign has been omitted from the formulas, as only the absolute values are considered in the following.
Mean free path of phonons
When the phonons move, they constantly collide with other phonons (lattice vibrations interfere with other lattice vibrations). Thus, even in solids there is a mean free path l for these quasi-particles. In this case, lattice defects determine the mean free path significantly. The more crystallographic defects there are, the smaller the mean free path, since the oscillations or phonons are scattered there, so to speak.

Mean free path in the direction of the heat flow
As already explained, the energetic propagation of the lattice vibration can be described by the migration of phonons. These phonons are permanently generated at the heat source and move through the material. The heat transfer in this model conception therefore equals the free motion of gas molecules. The moving phonons transfer energy by collisions with other phonons. In the following we will therefore look at heat conduction in non-metallic solids in a similar way to heat transfer in gases. Therefore the derived equation can also be used to estimate the thermal conductivity of gases!
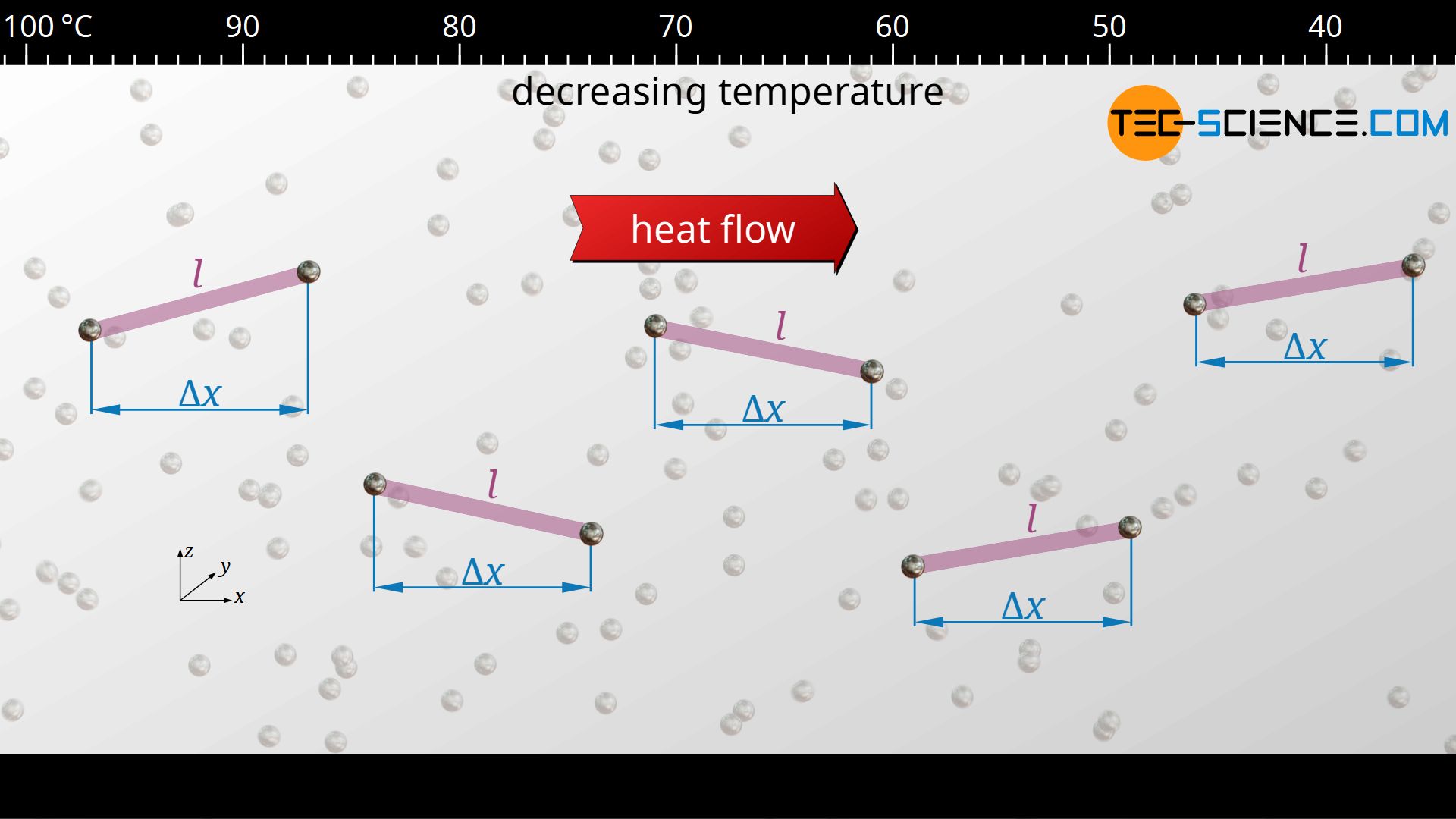
The mean time between two collisions of a phonon is denoted by τ. The average distance covered by the phonons corresponds to the mean free path l in three-dimensional space. In the case of heat conduction, however, only the movement of the phonons in the direction of the heat flow, i.e. the way traveled in x-direction, is relevant for energy transfer. The mean free path l is, however, linked to the mean free path components in the x-, y- and z-directions by the following relationship (“Pythagorean theorem in three-dimensional space”):
\begin{align}
& l = \sqrt{\Delta x^2+ \Delta y^2+ \Delta z^2} \\[5px]
& l^2 = \Delta x^2+ \Delta y^2+ \Delta z^2 \\[5px]
\end{align}
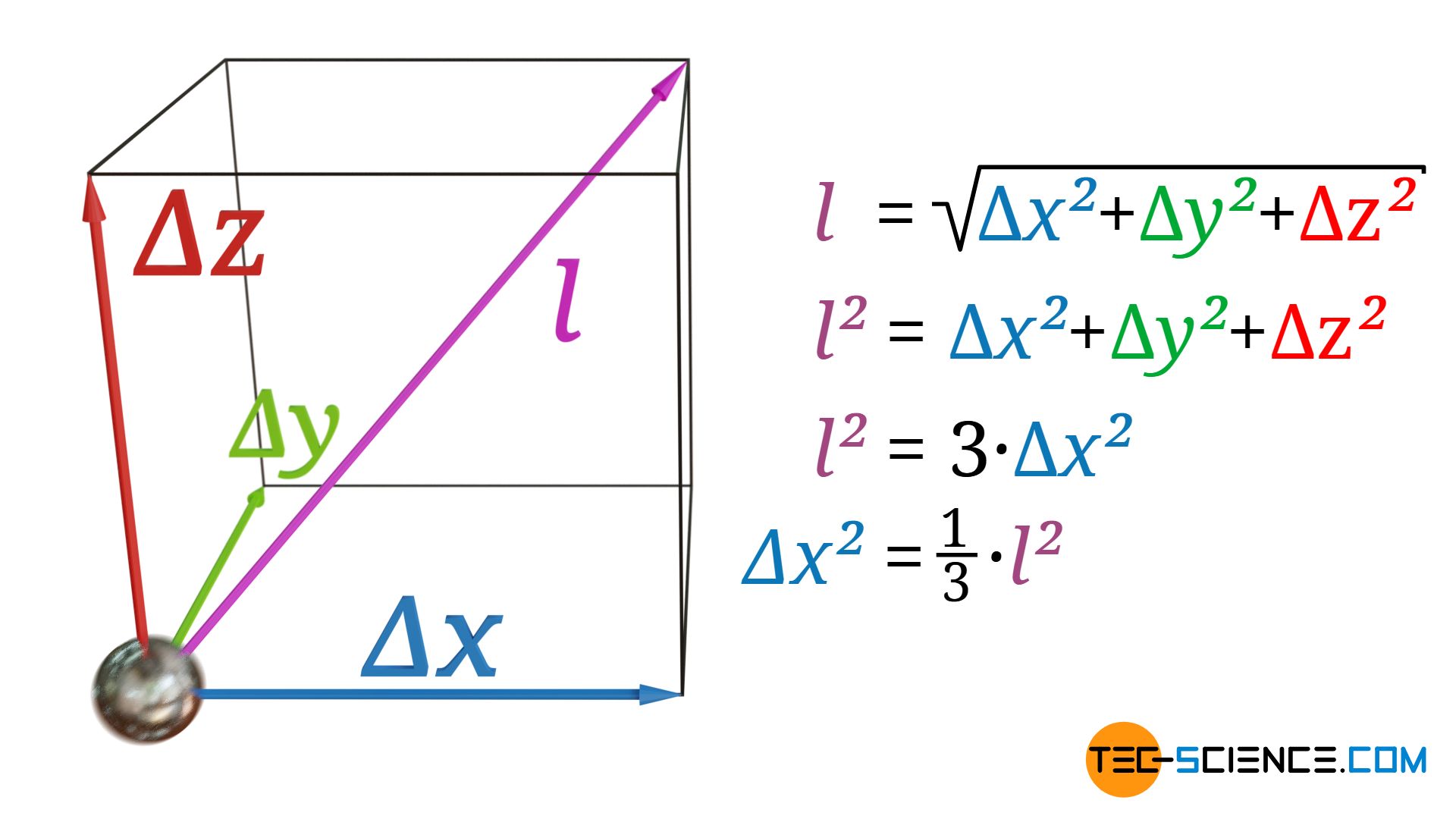
If an isotropic substance is assumed, then the phonons can move equally well in all three directions in space. On average, the phonons will therefore travel the same distance in x-direction as in y-direction or z-direction (Δx=Δy=Δz). The following relationship therefore applies between the mean free path l (in space) and the mean free path Δx (in x direction):
\begin{align}
& l^2 = \Delta x^2+ \Delta y^2+ \Delta z^2 ~~~~~\text{mit: } \Delta x = \Delta y = \Delta z ~~~\text{folgt:}\\[5px]
& l^2 = \Delta x^2+ \Delta x^2+ \Delta x^2 = 3 \cdot \Delta x^2 \\[5px]
\label{x}
& \underline{\Delta x^2 = \tfrac{1}{3} \cdot l^2} \\[5px]
\end{align}
Temperature decrease along the mean free path
In the steady state, temperature per unit length always decreases by the same amount, i.e. the temperature gradient is spatially constant. If this were not the case, then according to Fourier’s law, heat flows of varying magnitude would be obtained. However, this would mean that more heat flows in at one point than flows out at another point. This would result in a warming of the section under consideration. This is certainly the case at the beginning, as long as the material as a whole is still heating up and the temperatures are propagating (unsteady state).
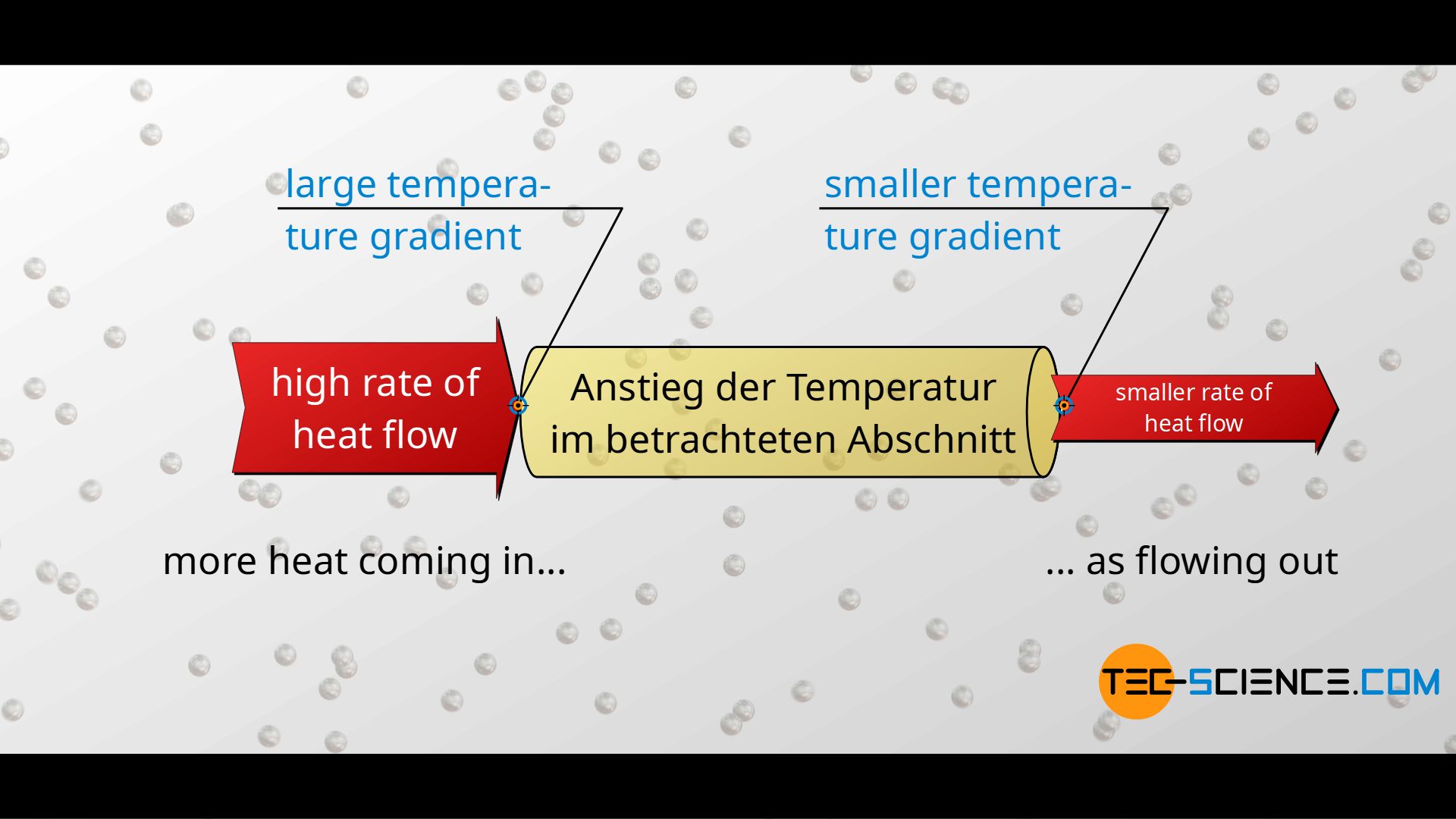
At some point, however, a state of equilibrium has been reached in which heat flows continuously through the material. The heat flow is then constant along the material in space and time and the temperature decreases constantly in space. In such a steady state it is then completely irrelevant which part of the material is being considered: Along a certain distance Δx, one always obtains the same temperature change ΔT, regardless of the location. Now we consider the distance Δx to be the mean free path in the x-direction. In this way each phonon thus undergoes on average the same temperature change ΔT, regardless of its position.
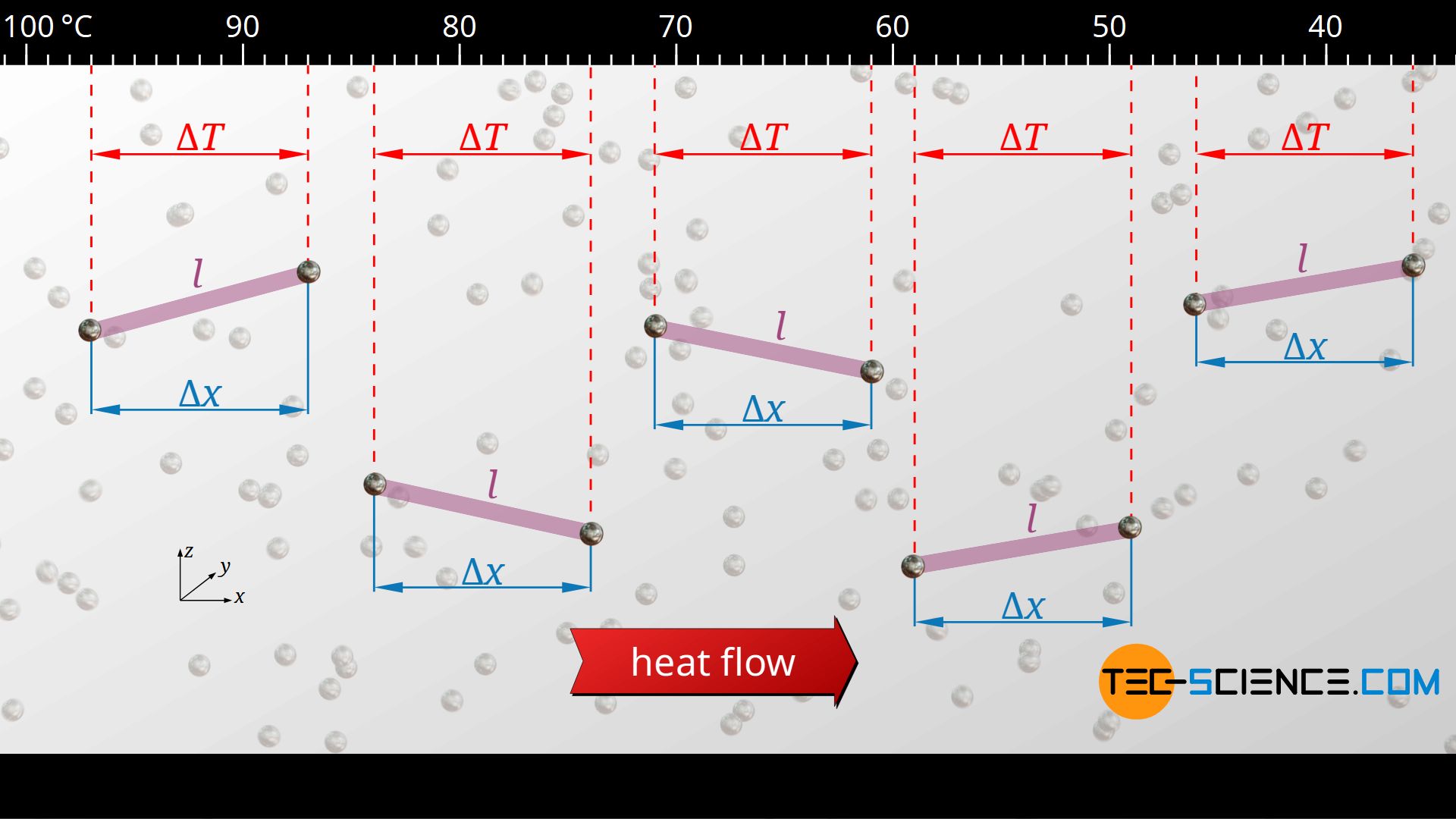
Energy transfer along the mean free path
Ultimately, the phonons are the carriers of thermal energy. They transfer their energy to other phonons from collision to collision and cool down, so to speak, by the amount ΔT as they travel the distance Δx. The phonon itself loses energy, but has transferred it to the next phonon. The total amount of such a heat transfer Q through an area A at a temperature change ΔT can be determined by the specific heat capacity cv of the material:
\begin{align}
\label{qq}
&Q = c_v \cdot m \cdot \Delta{T}\\[5px]
\end{align}
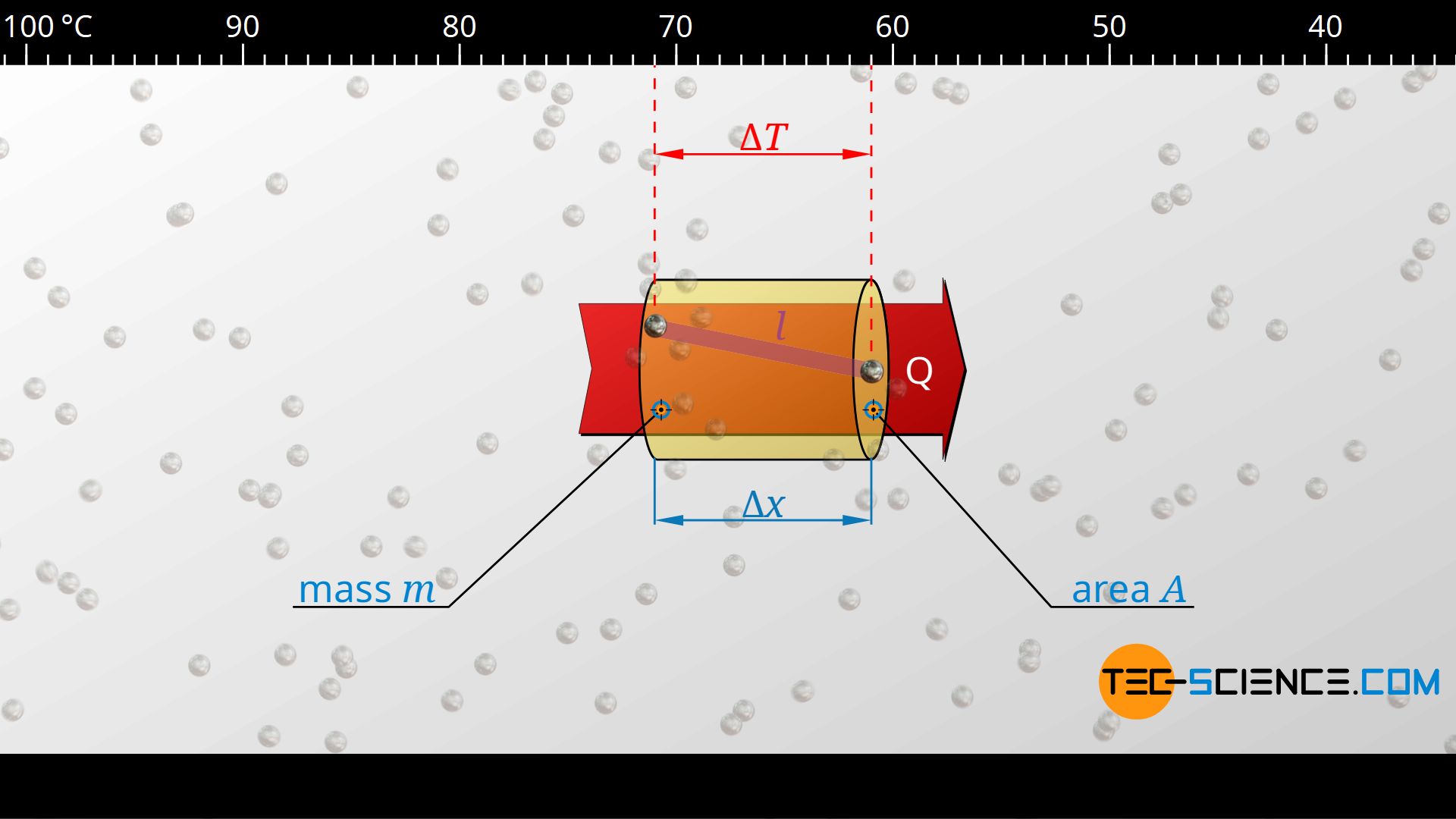
In the above formula, m denotes the mass contained in the volume, which is defined by the mean free path Δx and the (in principle arbitrary) area A. This mass can be determined by the density of the substance ϱ and the volume V=A⋅Δx:
\begin{align}
\label{m}
&m = \rho \cdot V = \rho \cdot A \cdot \Delta x \\[5px]
\end{align}
This simplified approach assumes that the phonons travel the distance Δx and thereby heat the mass m by ΔT. However, one can also look at the situation relative to the moving phonons, which might make things a bit clearer. From this point of view, the material flows past the phonons over the distance Δx. The phonons must obviously heat the mass m flowing past them by ΔT. This requires the heat Q described above.
Equation (\ref{m}) can finally be used in equation (\ref{qq}). For the amount of heat transferred Q applies:
\begin{align}
&Q = c_v \cdot \rho \cdot A \cdot \Delta x \cdot \Delta T \\[5px]
\end{align}
By definition, the mean distance Δx is covered within the mean time between two collisions τ. The heat Q is thus transferred within the time τ. The rate of heat flow through the considered area A is thus determined as follows:
\begin{align}
\label{xx}
&\dot Q = \frac{Q}{\tau} = \frac{ c_v \cdot \rho \cdot A \cdot \Delta x \cdot \Delta T }{\tau} \\[5px]
\end{align}
Thermal conductivity
Equation (\ref{xx}) for the heat flow through the area A can now be used in equation (\ref{q}) to determine the thermal conductivity λ:
\begin{align}
\require{cancel}
& \lambda = \frac{\dot Q \cdot \Delta x}{A \cdot \Delta T} \\[5px]
& \lambda = \frac{ c_v \cdot \rho \cdot \bcancel{A} \cdot \Delta x \cdot \bcancel{\Delta T} \cdot \Delta x}{\tau \cdot \bcancel{A} \cdot \bcancel{\Delta T}} \\[5px]
& \lambda = c_v \cdot \rho \cdot \frac{\Delta x^2}{\tau} \\[5px]
\end{align}
At this point, the relationship between the mean free path Δx and the mean free path l can be used:
\begin{align}
& \lambda = c_v \cdot \rho \cdot \frac{\Delta x^2}{\tau} = c_v \cdot \rho \cdot \frac{\tfrac{1}{3} \cdot l^2 }{\tau} = \tfrac{1}{3} \cdot c_v \cdot \rho \cdot \underbrace{\frac{l}{\tau}}_{=v} \cdot l \\[5px]
& \boxed{\lambda = \tfrac{1}{3} \cdot c_v \cdot \rho \cdot v \cdot l } \\[5px]
\end{align}
In the equation above the resulting quotient of mean free path l and mean time τ can be interpreted as the mean speed v of the phonons. This equation states that for non-metallic solids, the greater the mass-specific heat capacity and the greater the density, the greater the thermal conductivity. Both quantities can be combined to form a new volume-specific heat capacity Cv, which this time does not refer to mass but to volume (“heat capacity per unit volume”):
\begin{align}
\label{l}
& \boxed{\lambda = \tfrac{1}{3} \cdot C_v \cdot v \cdot l } ~~~~~\text{mit: }~~~ \boxed{C_v = c_v \cdot \rho} ~~~\text{heat capacity per unit volume}\\[5px]
\end{align}
This equation applies not only for estimating the thermal conductivity of non-metallic solids, but also for ideal gases!
A more detailed look at the thermal conductivity of ideal gases is given in the article Thermal conductivity of gases.
According to the above formula, the thermal conductivity of non-metallic solids depends on the volume-specific heat capacity. In this case it is advantageous for high thermal conductivity if the material is composed of very many but light molecules. However, the specific heat capacity is not a constant quantity, but is more or less strongly dependent on temperature, especially at relatively low temperatures. The mean free path is also strongly dependent on temperature, whereas the speed of the phonons is relatively independent of temperature and can therefore be regarded as almost constant! Which effects this has on the thermal conductivity of non-metals will be discussed in the next section.
Dependence of thermal conductivity on temperature
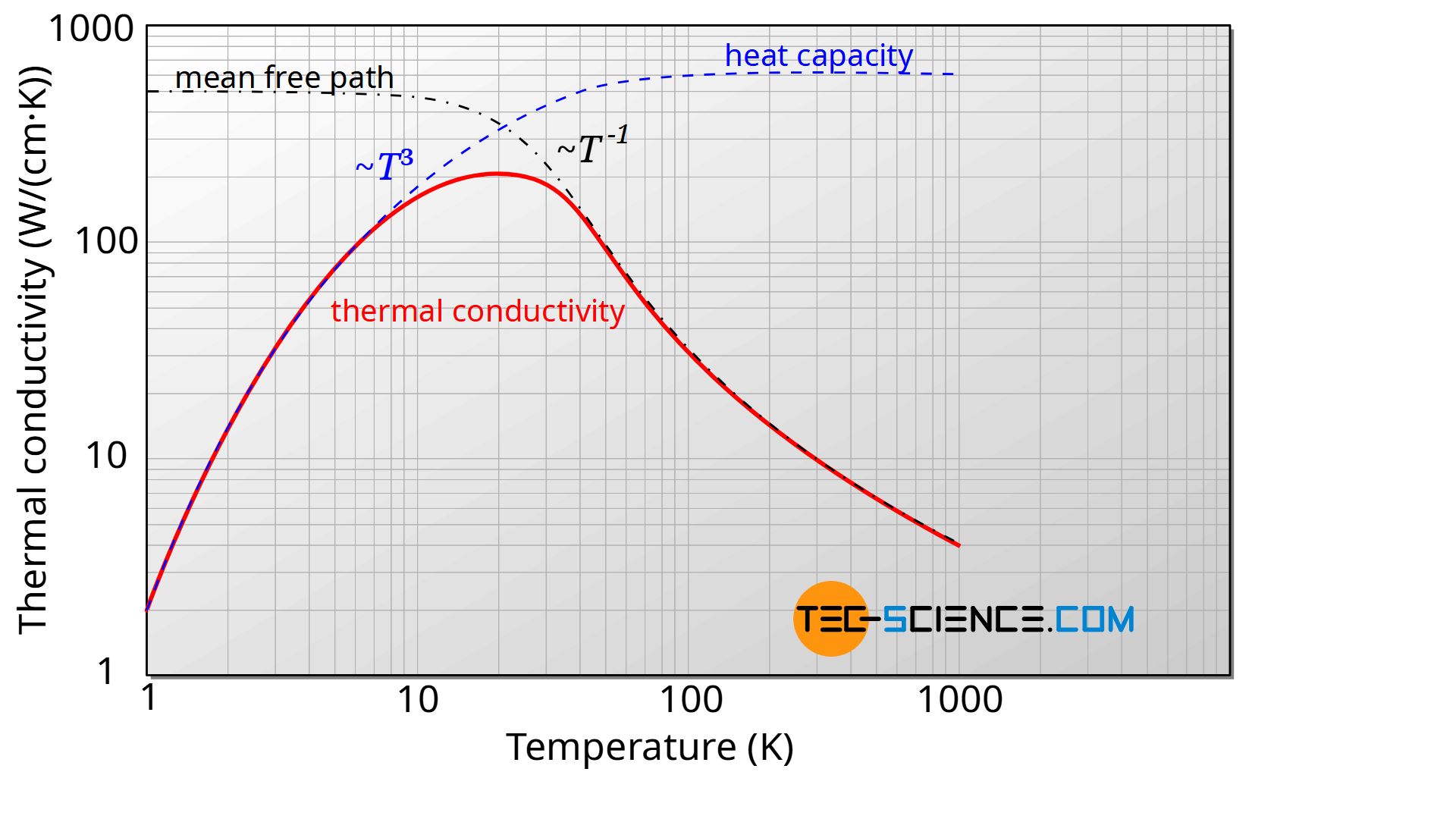
Lattice vibrations are ultimately sound waves that propagate through a material. In this respect, phonons propagate through the material at the speed of sound. This speed of propagation of the phonons can be regarded as relatively independent of the temperature in a first approximation. As far as the temperature dependence of the thermal conductivity is concerned, it is thus only influenced by the specific heat capacity and the mean free path. The diagram below shows the course of mean free path, heat capacity and the resulting thermal conductivity as a function of temperature. The course of the different values is described in more detail in the following.
Very low temperatures
In the article Internal Energy & Heat Capacity the temperature-dependent behavior of the specific heat capacity of solids has already been discussed in more detail. For many solids it is valid in a very good approximation that the molar heat capacity for very low temperatures near absolute zero first increases with the third power of temperature. After a transition phase, characterized by the so-called Debye temperature, the heat capacity then increases only slightly and can be regarded as almost independent of the temperature.
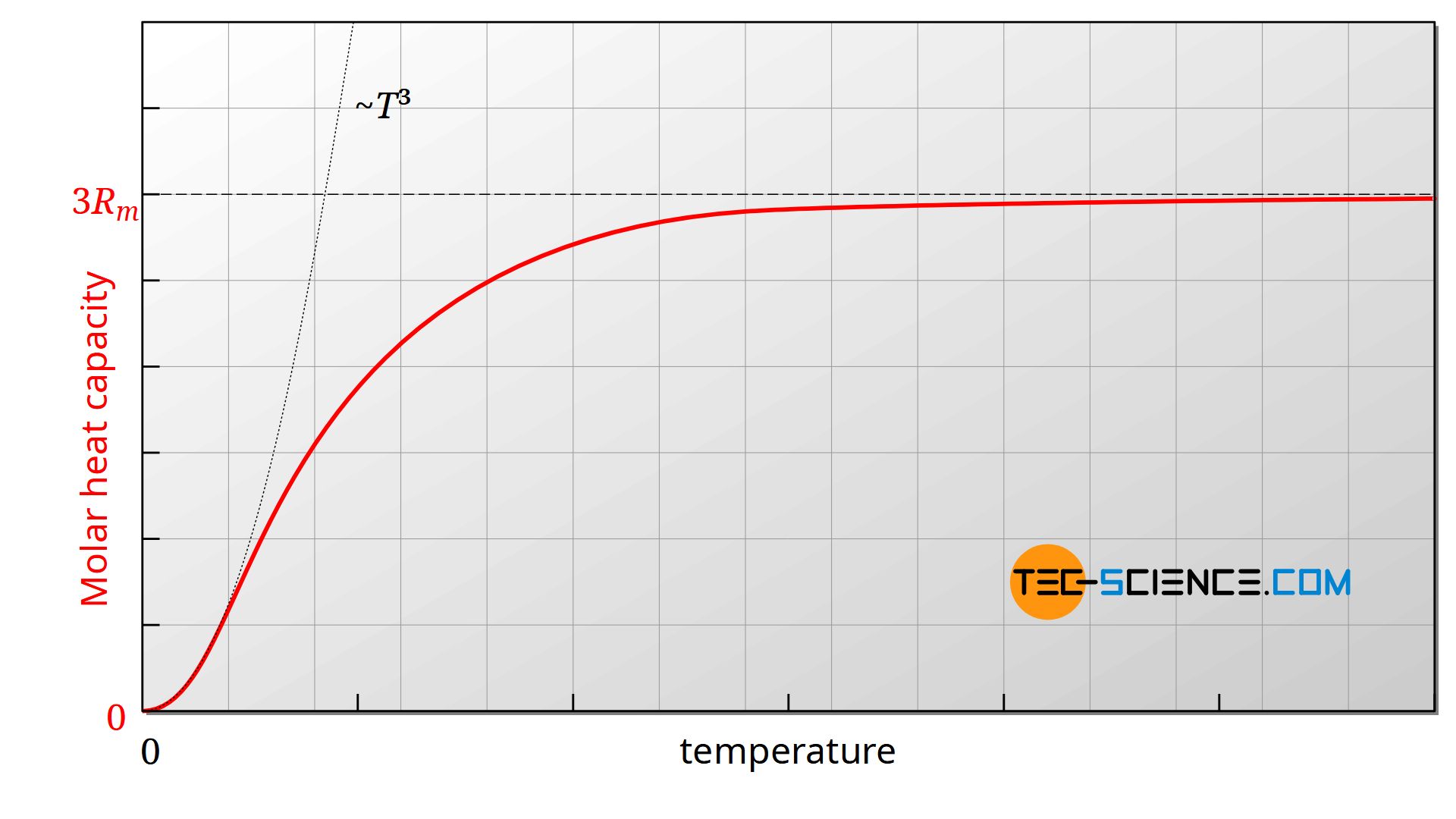
Note: According to the equation (\ref{l}), the thermal conductivity is expressed by the volume-specific heat capacity and not by the molar heat capacity. However, this does not change the statements made. The molar heat capacity and the volumetric heat capacity can be converted into each other using constant material properties. So it still remains the same: the heat capacity (whether mass-specific, volume-specific or molar) is proportional to the third power of temperature for very low temperatures and relatively independent of temperature for high temperatures.
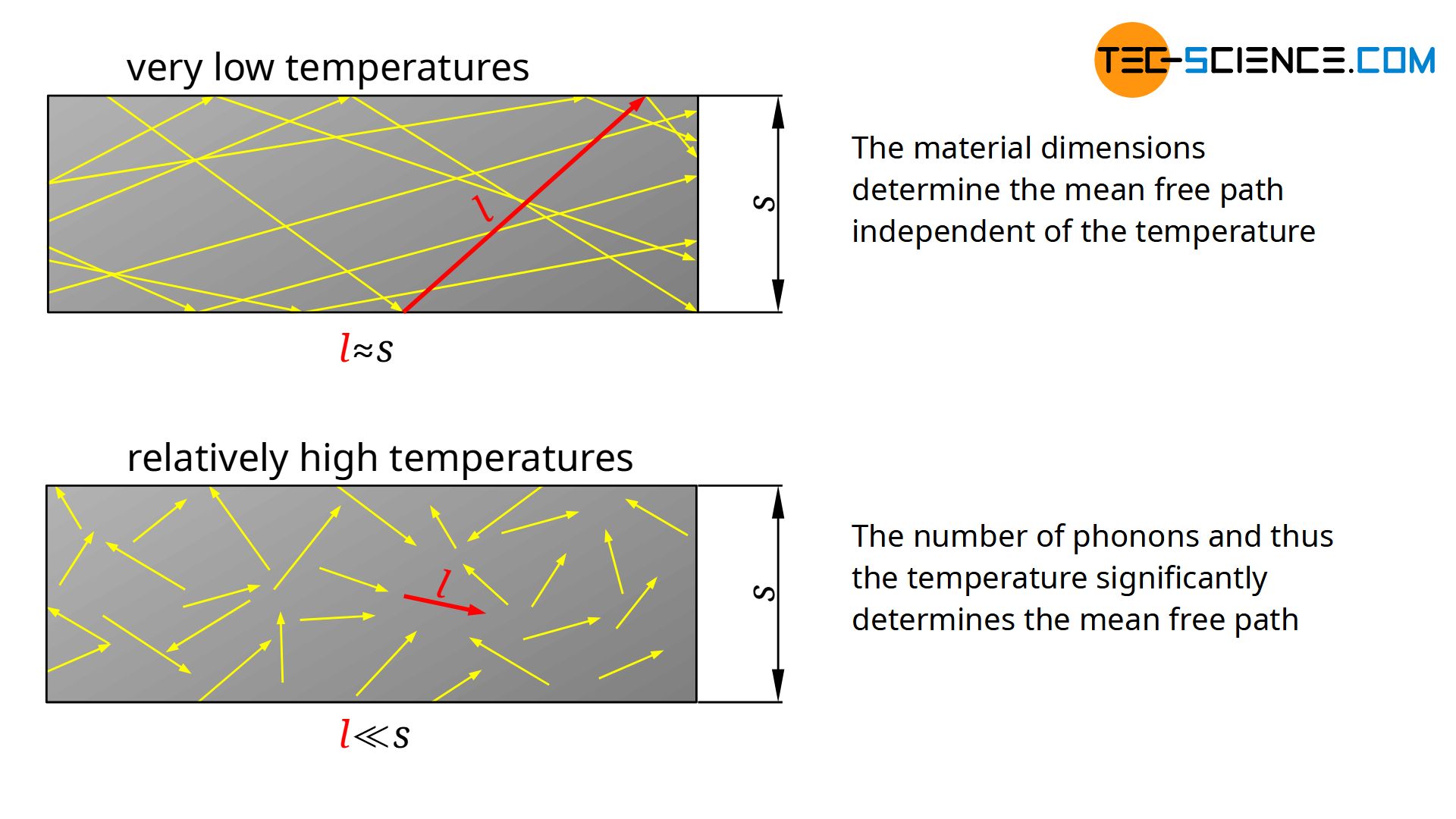
At very low temperatures the lattice structure does not vibrate strongly. Only a few phonons migrate through the material. The phonons practically do not influence each other. This means that the mean free path is relatively large and is basically only limited by the dimensions of the material or the density of crystallographic defects. Thus, for low temperatures, the mean free path is relatively independent of temperature, since it is only determined by the dimensions of the material.
So the fact that for low temperatures
- the speed of the phonons is relatively independent of temperature anyway, and
- the mean free path for very low temperatures also, but
- the heat capacity increases with the third power of the temperature,
führt dazu, dass die Wärmeleitfähigkeit ausgehend des absoluten Nullpunktes zunächst mit der dritten Potenz der Temperatur ansteigt.
leads to the fact that the thermal conductivity, starting from absolute zero, first increases with the third power of the temperature.
Relatively high temperatures
According to the law of Dulong-Petit, the molar heat capacity Cm with increasing temperature approaches more and more the three times the value of the molar gas constant Rm. The latter is determined by the Avogadro constant NA and the Boltzmann constant kB:
\begin{align}
& \boxed{C_m \approx 3 \cdot R_m = 3 \cdot N_A \cdot k_B} ~~~\text{law of Dulong-Petit} \\[5px]
\end{align}
Above the so-called Debye temperature, the heat capacity is therefore hardly dependent on the temperature. Although it is greater overall than at low temperatures, it is relatively constant.
At high temperatures, it is mainly the mean free path that influences the thermal conductivity (see figure above). In this case, many and relatively strong lattice vibrations occur, which influence each other very strongly, i.e. phonons are scattered at other phonons. In this case, the phonons only travel short distances before they are scattered at other phonons again.
The higher the temperature, the more phonons there are and the lower the mean free path. If the number of phonons is doubled, the mean free path has just halved. Above the Debye temperature, the phonon density is proportional to the temperature and the mean free path is therefore inversely proportional to the temperature.
So the fact that for high temperatures
- the speed of the phonons can still be regarded as constant, and
- the heat capacity according to the Dulong-Petit law is also independent of the temperature,
- but the mean free path is inversely proportional to the temperature,
causes the thermal conductivity at high temperatures to decrease reciprocally with temperature.
Above the Debye temperature, the thermal conductivity of crystalline non-metallic solids decreases reciprocally with temperature!
Low temperatures
At low temperatures, which do not represent to the limiting cases as described above, the thermal conduction is ultimately limited by the mean free path, which results from the scattering of the phonons at the lattice structure or at defects (also called Umklapp scattering, U-process or Umklapp process). The transition between the limiting cases is usually in the low two-digit Kelvin range.
The number of phonons involved in such a process of Umklapp scattering decreases exponentially with decreasing temperature below the Debye temperature. This finally results in an increase of the mean free path, until at sufficiently low temperatures the mean free path is limited only by the dimensions of the material or the density of defects. However, this also means that the thermal conductivity at very low temperatures depends on the sample geometry! Wider samples with a correspondingly larger mean free path have higher thermal conductivity values than narrower samples!
Amorphous solids
Even in amorphous solids, a dependence of the thermal conductivity with increasing temperature can be found in principle. However, the mean free path is relatively independent of the temperature. This is due to the fact that amorphous solids do not have a regular crystalline structure, but have permanent “crystallographic” defects. In this respect, the mean free path of amorphous solids is always in the order of atomic spacing, regardless of temperature.
The fact that the thermal conductivity of amorphous materials also changes with increasing temperature is largely due to the change in heat capacity. The temperature dependencies are, however, somewhat different from those of crystalline materials. In particular, the heat capacity near absolute zero no longer increases with the third power of temperature, but usually much less.
The heat capacity of amorphous materials is often greater than that of crystalline materials, but the mean free path is significantly smaller. This usually results in a lower thermal conductivity compared to crystalline materials.






