Die Wärmeleitfähigkeit in kristallinen, nicht-metallischen Feststoffen nimmt steigender Temperatur zunächst zu und dann wieder ab.
Phononen: Quasiteilchen der Gitterschwingungen
Unter Wärmeleitung versteht man den Transport von thermischer Energie durch einen Stoff hindurch. In Gasen und Flüssigkeiten handelt es sich bei den energieübertragenden Teilchen, um jene Teilchen die sich frei bewegen können. Durch Stoßprozesse wird auf diese Weise Energie von einem Teilchen auf ein anderes übertragen und somit durch den Stoff geleitet. Wie sieht dies nun aber in Festkörpern aus? In metallischen Festkörpern gibt es tatsächlich auch solche freien Teilchen. Dies sind die freien Leitungselektronen des Elektronengases, die maßgeblich für die gute Wärmeleitfähigkeit verantwortlich sind.
In nichtmetallischen Festkörpern gibt es zwar keine realen freien Teilchen, aber dafür sind die ortsgebundenen Teilchen über Bindungskräfte elastisch miteinander gekoppelt. Wärmeübertragung kann man in solchen Fällen als ein Übertragen von Schwingungsenergie von einem zum nächsten Teilchen betrachten.

Aus der Quantenphysik weiß man, dass man jeder Welle auch einen entsprechenden Impuls zuordnen kann (deBroglie-Beziehung). Dieser Impuls verhält sich im Prinzip wie der Impuls eines gedachten Teilchens. Diese Quasiteilchen werden auch als Phononen bezeichnet. Die Gitterschwingung und damit die Phononen werden letztlich kontinuierlich an der Wärmequelle erzeugt und bewegen sich durch das Material. Auf die analoge Weise wie die Energieübertragung bei einer Wärmestrahlung durch Photonen beschrieben wird, kann die Wärmeübertragung bei der Wärmeleitung durch Phononen beschrieben werden.
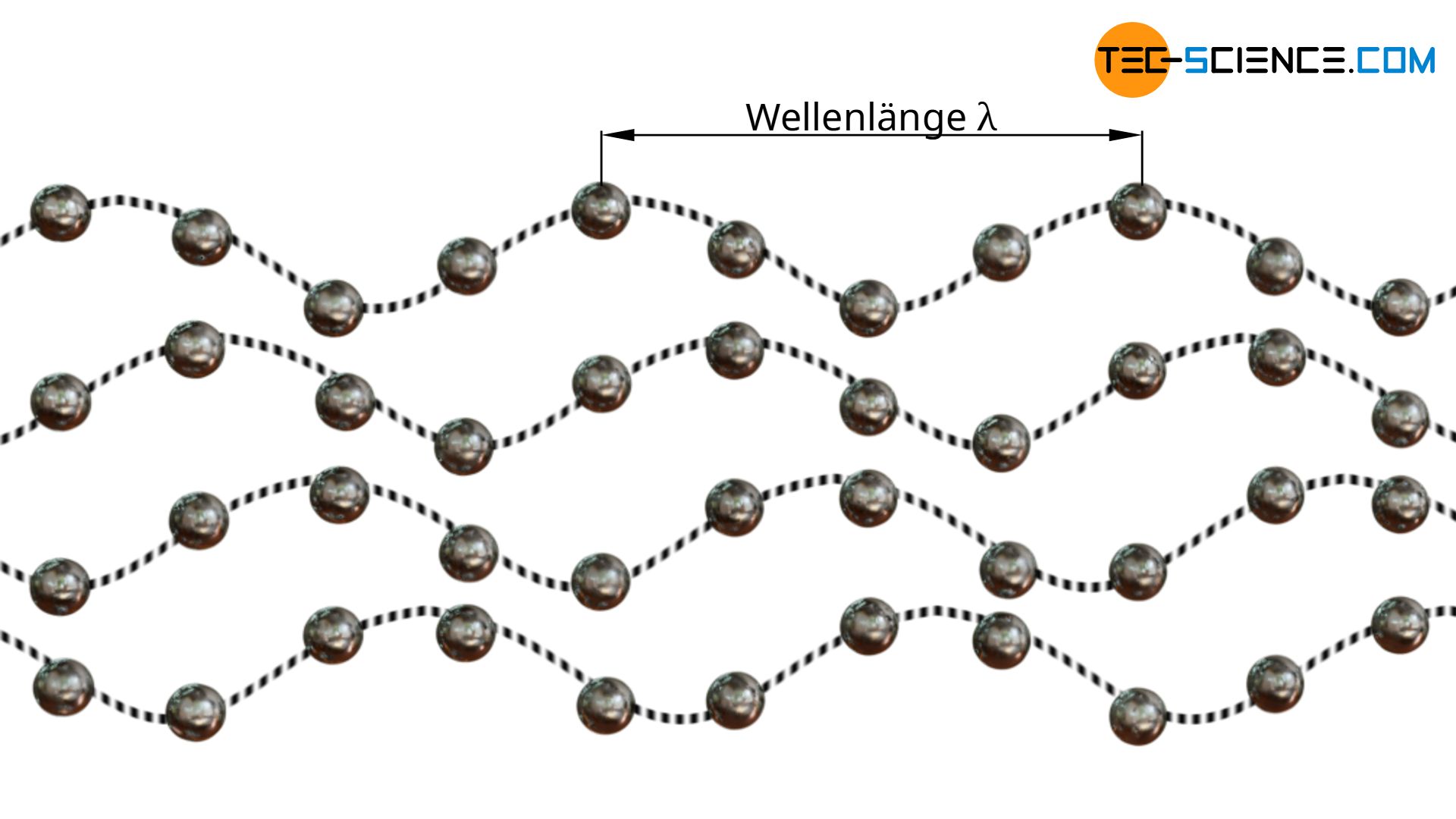
Auf die analoge Weise wie die Photonen die Quasiteilchen einer elektromagnetischen Welle darstellen, so entsprechen die Phononen den Quasiteilchen einer Materiewelle (Gitterschwingung).
Deshalb kann man sich den Transport von Schwingungsenergie in nichtmetallischen Festkörpern ebenfalls als eine Bewegung von Teilchen auffassen: die Bewegung der Phononen (Energiequanten). Auf diese Weise kann man die gesamte Wärmeleitung sowohl in Gasen, Flüssigkeiten, als auch in Feststoffen als Energieübertragung von kollidierenden Teilchen beschreiben (Energiediffusion).
Wärmeleitung in Metallen
In Metallen sind im Übrigen nicht nur die freien Elektronen des Elektronengases an der Wärmeleitung beteiligt, sondern eben auch die schwingende Gitterstruktur, d.h. die Phononen! Beides zusammen macht Metalle deshalb im Allgemeinen zu sehr guten Wärmeleitern. Im Artikel Wärmeleitfähigkeit sind einige Werte von ausgewählten Stoffen gegeben.
Herleitung der Wärmeleitfähigkeit von nichtmetallischen Feststoffen
Wärmeleitfähigkeit
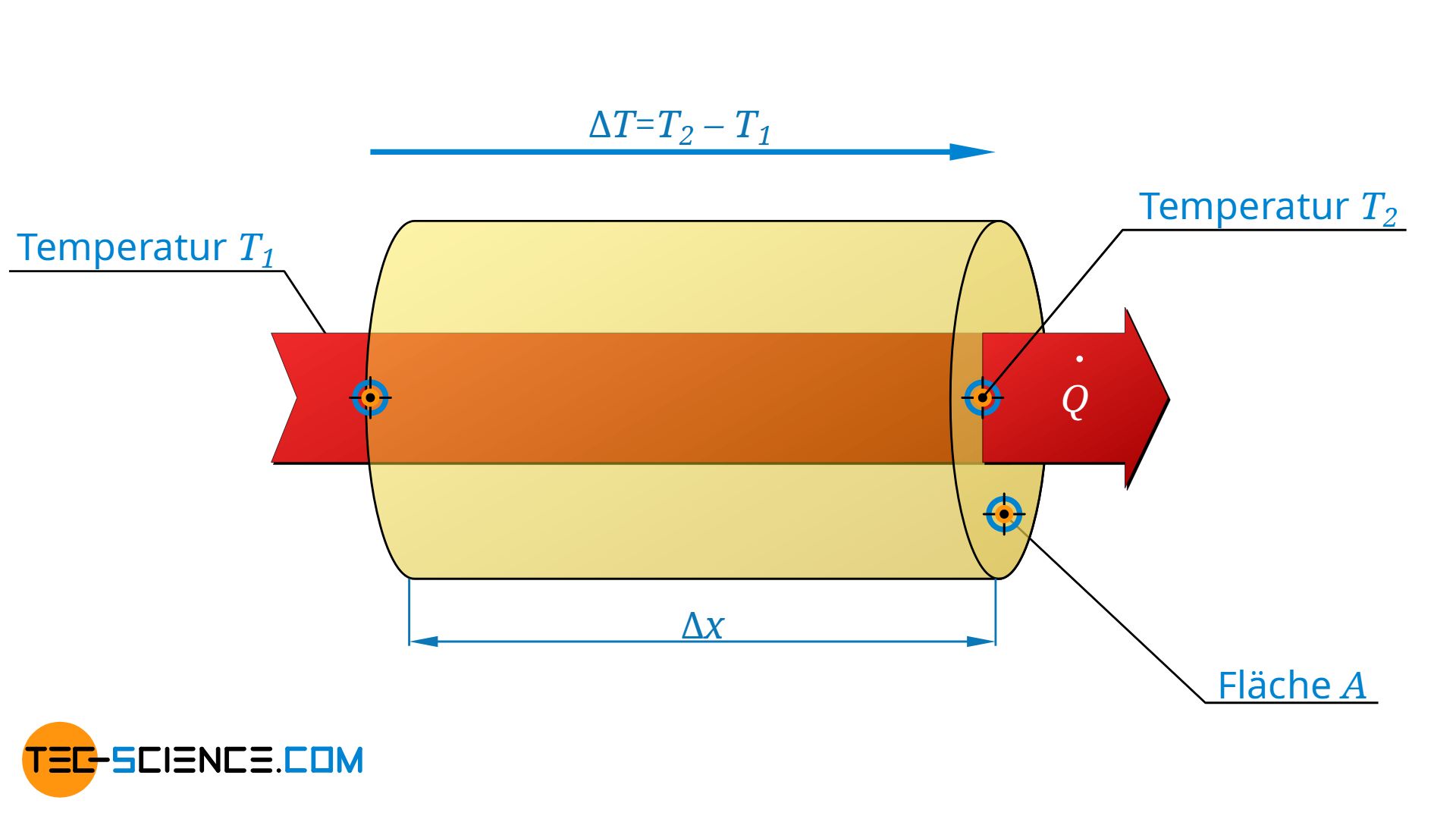
Für ein wärmeleitendes Material mit der Wärmeleitfähigkeit λ bestimmt sich der durch die Fläche A hindurchtretende Wärmestrom Q* über den dort vorhandenen Temperaturgradienten, d.h. über das Temperaturgefälle ΔT entlang der Strecke Δx (Fourier’sches Gesetz). Die Wärmeleitfähigkeit lässt sich hieraus wie folgt ermitteln:
\begin{align}
& \boxed{\dot Q = \lambda \cdot A \cdot \frac{\Delta T}{\Delta x}} ~~~\text{Fourier’sches Gesetz} \\[5px]
\label{q}
& \lambda = \frac{\dot Q \cdot \Delta x}{A \cdot \Delta T} \\[5px]
\end{align}
Anmerkung: In den Formeln wurde der Einfachheit halber auf das negative Vorzeichen verzichtet, da im Folgenden nur die Beträge der Größen betrachtet werden.
Mittlere freie Weglänge von Phononen
Bei der Bewegung der Phononen im Phononenmodell kollidieren diese ständig mit anderen Phononen. Somit gibt es auch in Festkörpern eine mittlere freie Weglänge ldieser Quasiteilchen. Gitterdefekte bestimmen in diesem Fall maßgeblich die mittlere freie Weglänge. Je mehr Gitterdefekte vorhanden sind, desto geringer die mittlere freie Weglänge, da die Schwingungen bzw. Phononen dort sozusagen gestreut werden.

Mittlere freie Wegstrecke in Richtung des Wärmestroms
Wie bereits erläutert, lässt sich die energetische Ausbreitung der Gitterschwingung im Phononenmodell durch die Bewegung von Phononen beschreiben. Diese werden an der Wärmequelle permanent erzeugt und bewegen sich durch das Material. Die Wärmeübertragung gleicht in diesem Modell also der freien Bewegung von Gasteilchen. Die sich bewegenden Phononen übertragen dabei durch Stoßprozesse Energie. Wir betrachten im Folgenden also die Wärmeleitung in nichtmetallischen Festkörpern analog zur Wärmeübertragung in Gasen. Deshalb kann die hergeleitete Gleichung auch zur Abschätzung der Wärmeleitfähigkeit von Gasen verwendet werden!
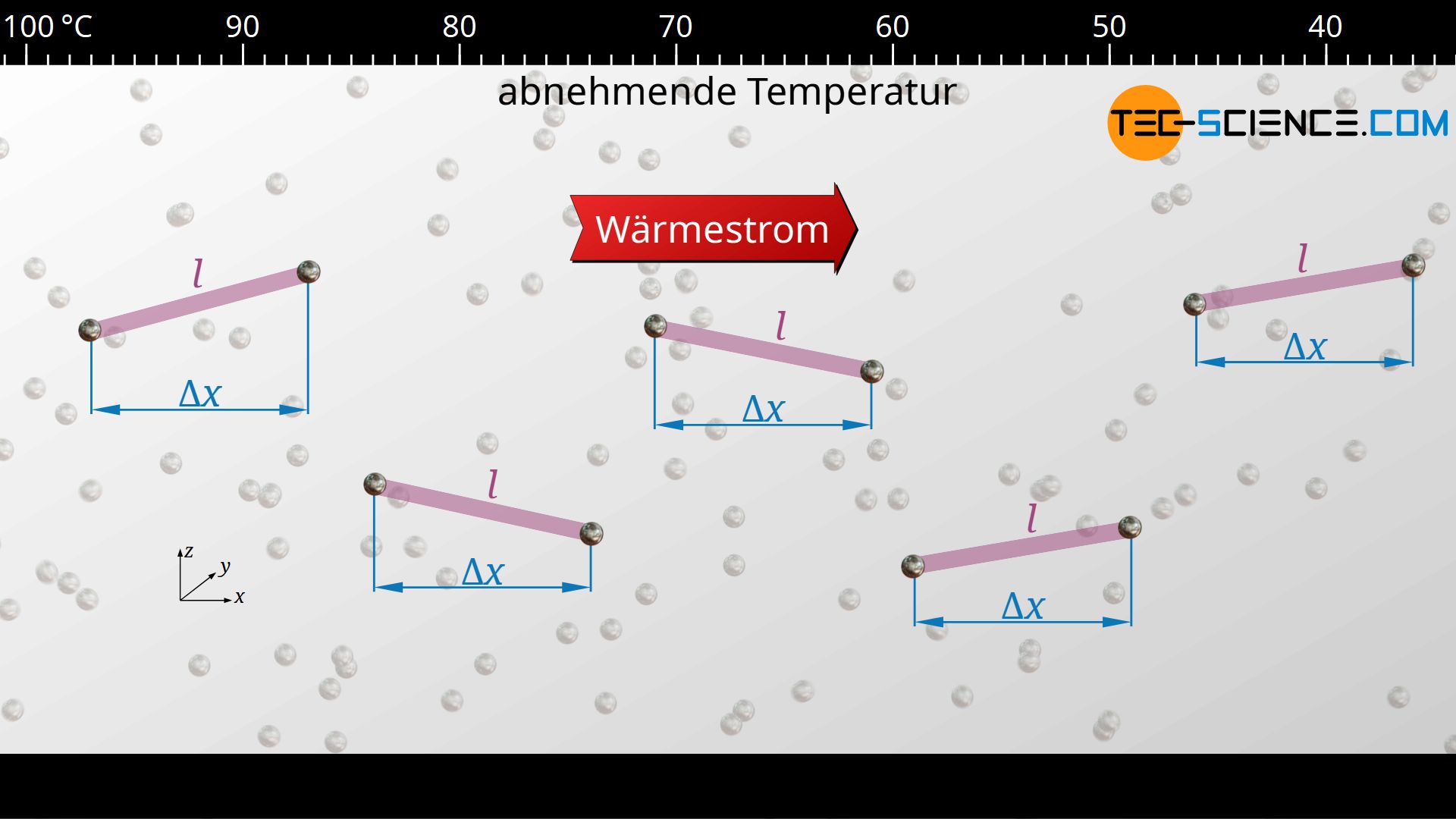
Die mittlere Zeitdauer zwischen zwei Kollisionen eines Phonons wird im Folgenden mit τ bezeichnet. Die dabei im Mittel zurückgelegte Wegstrecke der Phononen entspricht der mittleren freien Wegstrecke l. Diese mittlere freie Weglänge bezieht sich dabei auf die Bewegung Phononen im dreidimensionalen Raum. Relevant für die Energieübertragung ist in diesem Fall jedoch nur die Bewegung der Phononen in Richtung des Wärmestrom, d.h. die Bewegungskomponente in x-Richtung. Die mittlere freie Weglänge l ist dabei jedoch über folgende Beziehung mit den mittleren freien Wegkomponenten in x-, y- und z-Richtung verknüpft („Satz des Pythagoras im dreidimensionalen Raum“):
\begin{align}
& l = \sqrt{\Delta x^2+ \Delta y^2+ \Delta z^2} \\[5px]
& l^2 = \Delta x^2+ \Delta y^2+ \Delta z^2 \\[5px]
\end{align}
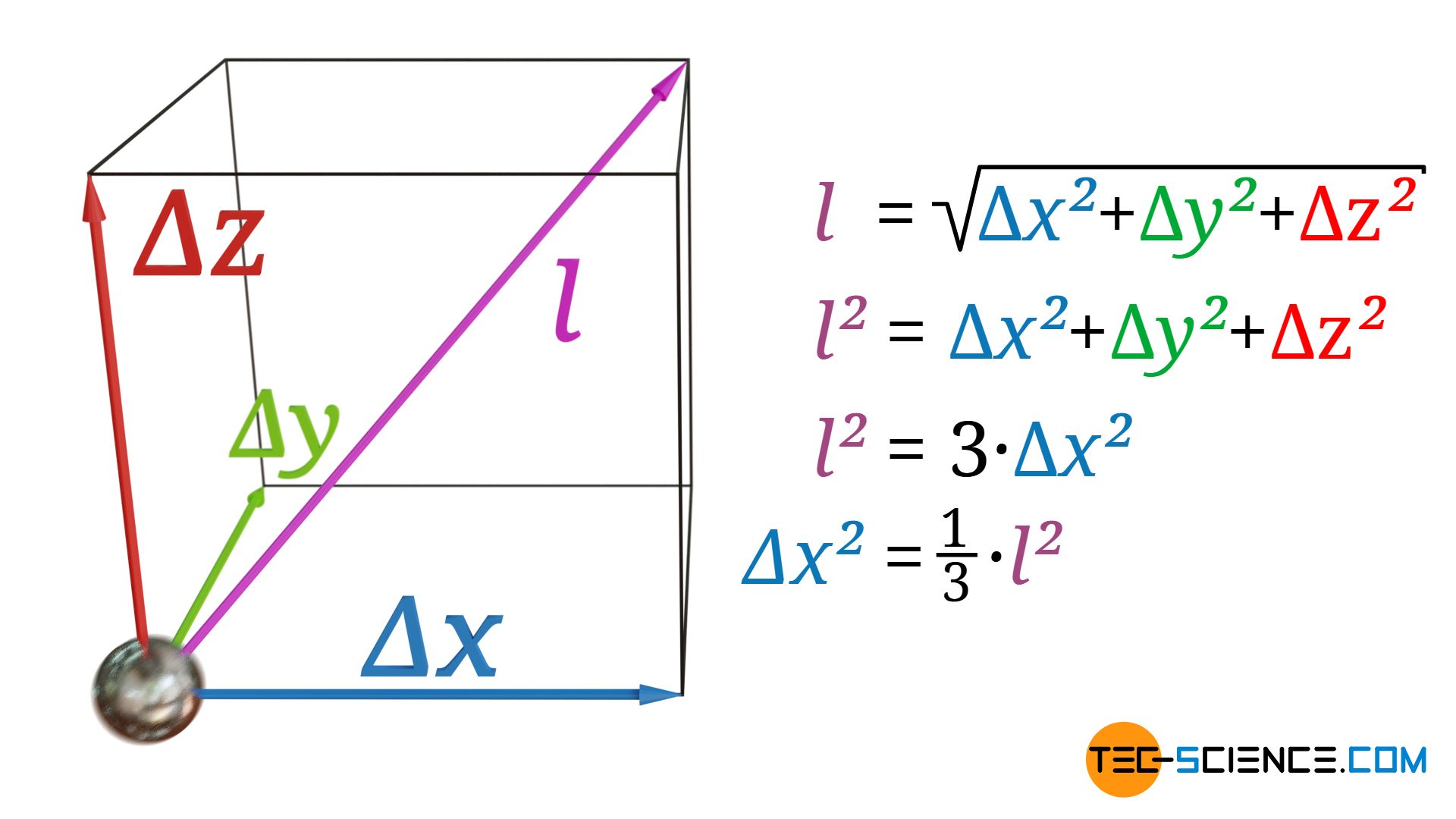
Wird ein isotroper Stoff vorausgesetzt, dann können sich die Phononen in alle drei Raumrichtungen gleichermaßen gut bewegen. Zwischen zwei Kollisionen, werden die Phononen im zeitlichen Mittel deshalb dieselbe Wegstrecke in x-Richtung wie in y-Richtung oder z-Richtung zurücklegen (Δx=Δy=Δz). Somit gilt folgender Zusammenhang zwischen der mittleren freien Wegstrecke l (im Raum) und der mittleren freien Wegstrecke Δx (in x-Richtung):
\begin{align}
& l^2 = \Delta x^2+ \Delta y^2+ \Delta z^2 ~~~~~\text{mit: } \Delta x = \Delta y = \Delta z ~~~\text{folgt:}\\[5px]
& l^2 = \Delta x^2+ \Delta x^2+ \Delta x^2 = 3 \cdot \Delta x^2 \\[5px]
\label{x}
& \underline{\Delta x^2 = \tfrac{1}{3} \cdot l^2} \\[5px]
\end{align}
Temperaturabnahme entlang der mittleren freien Wegstrecke
Im stationären Zustand nimmt Temperatur pro Längeneinheit immer um denselben Betrag ab, d.h. der Temperaturgradient ist räumlich konstant. Wäre dies nicht so, dann erhielte man gemäß des Fourier’schen Gesetzes unterschiedlich große Wärmeströme. Dies würde dann aber bedeuten, dass ein einer Stelle mehr Wärme einströmt, als an anderer Stelle abströmt. Es käme folglich zu einer Erwärmung, des betrachteten Abschnittes. Dies ist zu Beginn sicherlich der Fall, solange sich das Material insgesamt noch erwärmt und sich die Temperaturen ausbreiten (instationärer Zustand).
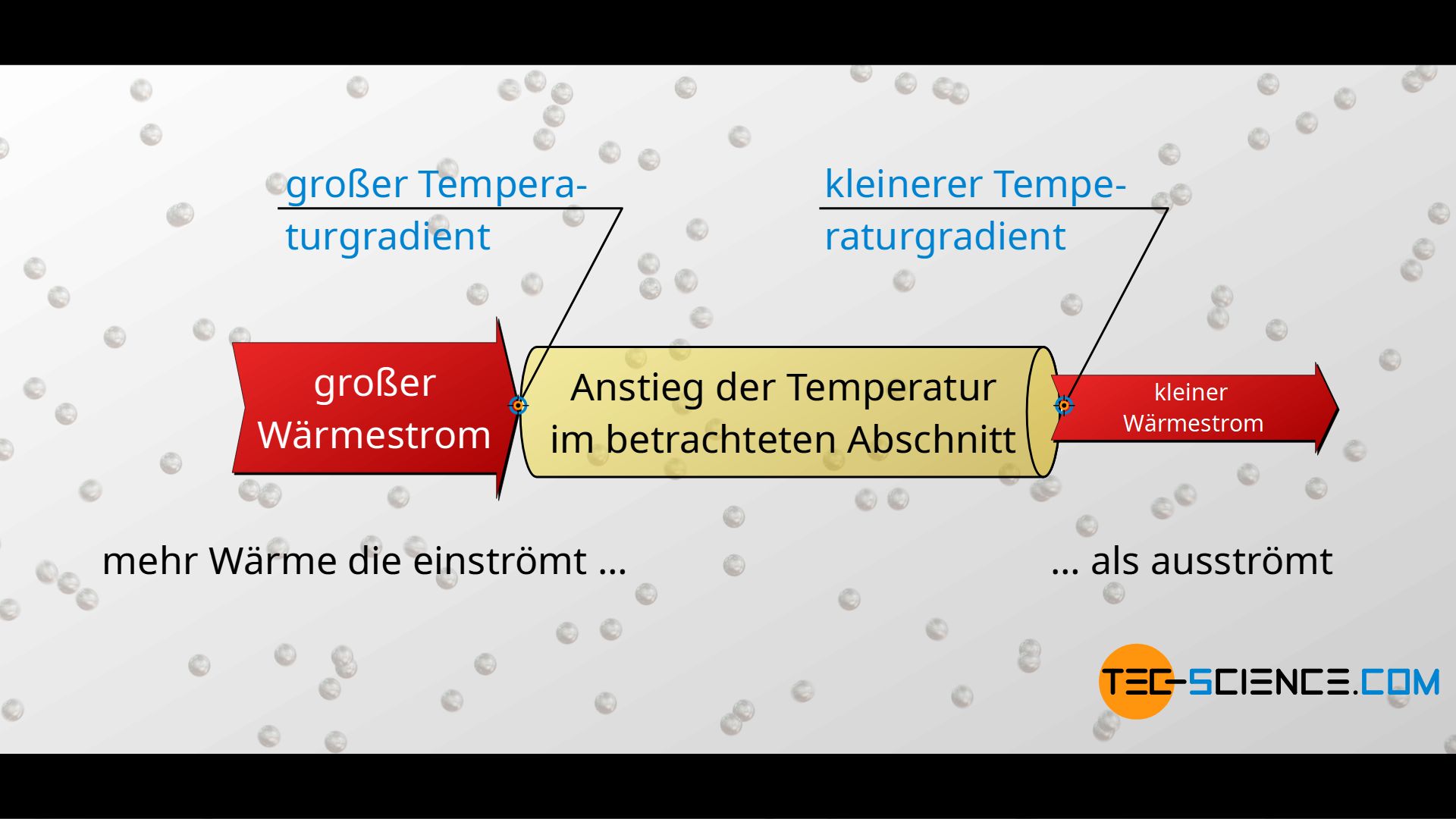
Irgendwann hat sich aber ein Gleichgewichtszustand eingestellt, bei der Wärme kontinuierlich durch den Stoff strömt. Der Wärmestrom ist dann entlang des Materials räumlich und zeitlich konstant und die Temperatur nimmt räumlich konstant ab. In einem solchen stationären Zustand ist es dann völlig egal welche Stelle des Materials man betrachtet: Auf eine bestimmte Länge Δx, erhält man unabhängig des Ortes stets dieselbe Temperaturänderung ΔT. Die Wegstrecke Δx soll in diesem Fall der mittlere freien Weglänge in x-Richtung entsprechen. Bezogen auf diese mittlere freie Wegkomponente Δx durchläuft im zeitlichen Mittel somit jedes Phonon unabhängig vom Ort stets dieselbe Temperaturänderung ΔT.
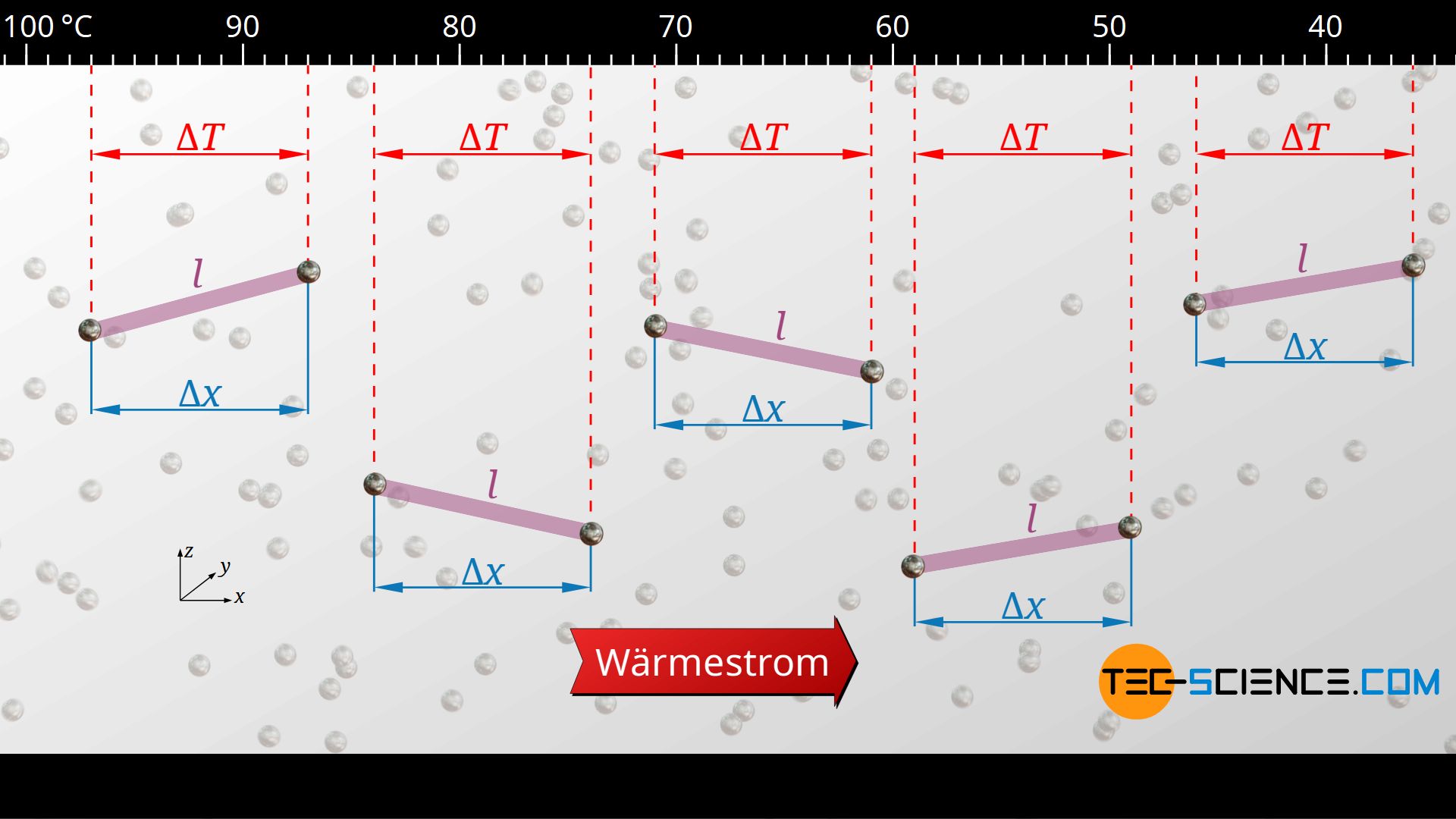
Energieübertragung entlang der mittleren freien Wegstrecke
Letztlich sind die Phononen Träger der Wärmeenergie. Sie übertragen ihre Energie von Stoß zu Stoß auf andere Phononen und kühlen sozusagen beim Durchlaufen der Strecke Δx um den Betrag ΔT ab. Das Phonon verliert hierdurch selbst Energie, hat es aber auf das nächste Phonon übertragen. Wie groß ein solcher Wärmetransfer Q durch eine Fläche A bei einer Temperaturänderung ΔT insgesamt sein muss, lässt sich über die spezifische Wärmekapazität cv des Stoffes ermitteln:
\begin{align}
\label{qq}
&Q = c_v \cdot m \cdot \Delta{T}\\[5px]
\end{align}
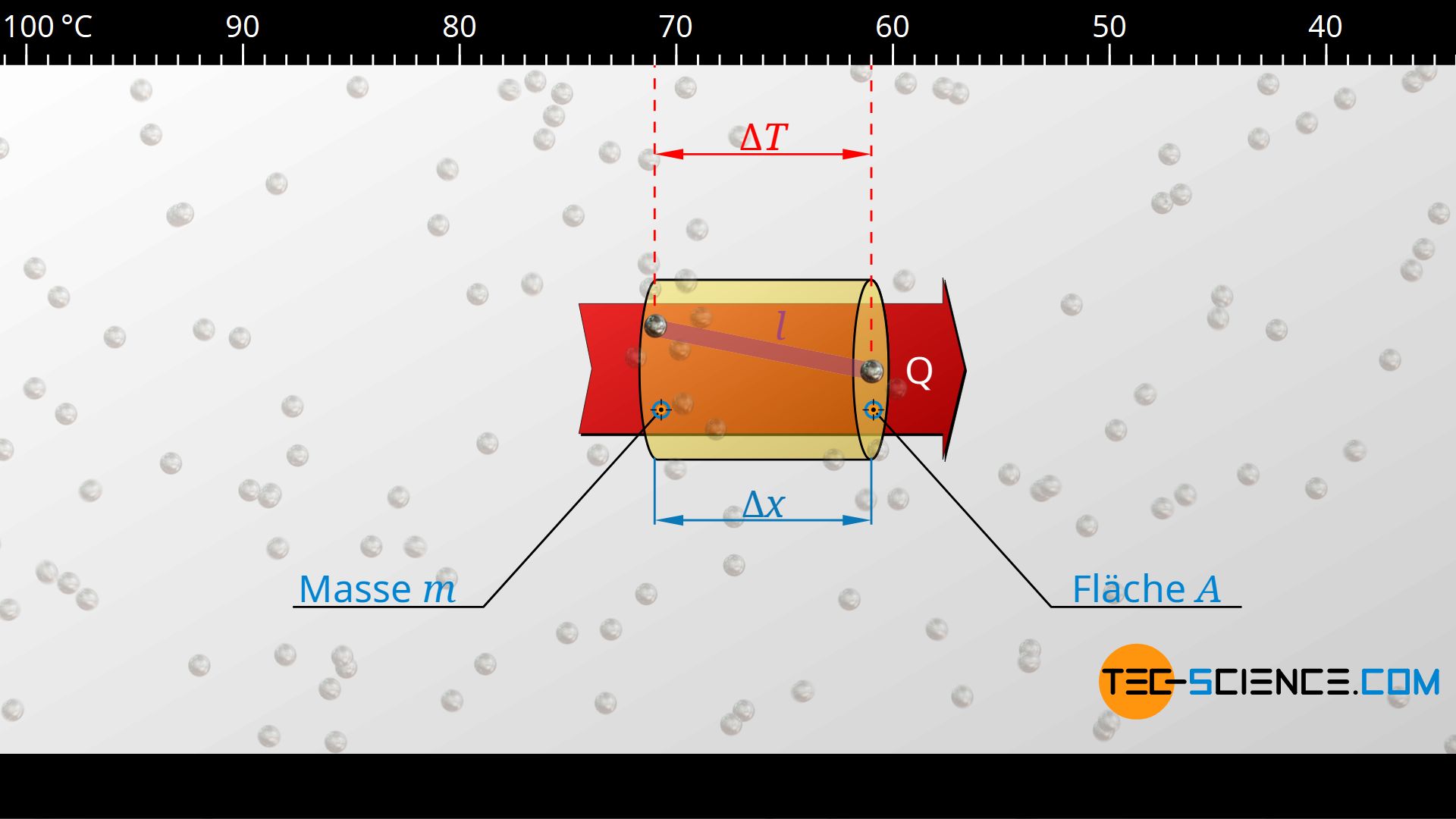
In der oberen Formel bezeichnet m die Masse, die sich in jenem Volumen befindet, die sich über die mittlere freie Wegstrecke Δx und die (prinzipiell beliebige) Fläche A ergibt. Diese Masse kann über die Dichte des Stoffes ϱ und das Volumen V=A⋅Δx bestimmt werden:
\begin{align}
\label{m}
&m = \rho \cdot V = \rho \cdot A \cdot \Delta x \\[5px]
\end{align}
Die obere Betrachtungsweise geht vom Strömen der Phononen über die Strecke Δx aus, die dabei die Masse m um ΔT erwärmen. Man kann die Situation aber auch relativ zu den bewegten Phononen betrachten, was die Sache vielleicht etwas anschaulicher macht. Aus dieser Sichtweise heraus strömt das Material über die Strecke Δx an den Phononen vorbei. Die Phononen müssen die dabei vorbeiströmende Masse m offensichtlich um ΔT erwärmen. Hierfür ist die oben beschriebene Wärme Q nötig.
Gleichung (\ref{m}) kann schließlich noch in Gleichung (\ref{qq}) eingesetzt werden. Für den transportierten Wärmebetrag Q gilt somit:
\begin{align}
&Q = c_v \cdot \rho \cdot A \cdot \Delta x \cdot \Delta T \\[5px]
\end{align}
Das Zurücklegen der mittleren Wegstrecke Δx geschieht per Definition innerhalb der Zeit zwischen zwei Stößen τ. Die Wärme Q wird also innerhalb der Zeit τ übertragen. Die Wärmeleistung durch die betrachtete Fläche A bestimmt sich somit wie folgt:
\begin{align}
\label{xx}
&\dot Q = \frac{Q}{\tau} = \frac{ c_v \cdot \rho \cdot A \cdot \Delta x \cdot \Delta T }{\tau} \\[5px]
\end{align}
Wärmeleitfähigkeit
Die obere Gleichung (\ref{xx}) für den Wärmestrom durch die Fläche A kann nun in Gleichung (\ref{q}) zur Bestimmung der Wärmeleitfähigkeit λ eingesetzt werden:
\begin{align}
\require{cancel}
& \lambda = \frac{\dot Q \cdot \Delta x}{A \cdot \Delta T} \\[5px]
& \lambda = \frac{ c_v \cdot \rho \cdot \bcancel{A} \cdot \Delta x \cdot \bcancel{\Delta T} \cdot \Delta x}{\tau \cdot \bcancel{A} \cdot \bcancel{\Delta T}} \\[5px]
& \lambda = c_v \cdot \rho \cdot \frac{\Delta x^2}{\tau} \\[5px]
\end{align}
An dieser Stelle kann nun noch die Beziehung zwischen der mittleren freien Wegkomponente Δx und der mittleren freien Wegstrecke l genutzt werden:
\begin{align}
& \lambda = c_v \cdot \rho \cdot \frac{\Delta x^2}{\tau} = c_v \cdot \rho \cdot \frac{\tfrac{1}{3} \cdot l^2 }{\tau} = \tfrac{1}{3} \cdot c_v \cdot \rho \cdot \underbrace{\frac{l}{\tau}}_{=v} \cdot l \\[5px]
& \boxed{\lambda = \tfrac{1}{3} \cdot c_v \cdot \rho \cdot v \cdot l } \\[5px]
\end{align}
In der oberen Gleichung wurde das Quadrat der mittleren freien Wegstrecke ausgeschrieben (l²=l⋅l), sodass der sich hierdurch ergebende Quotient aus mittlerer freier Wegstrecke l und Zeitdauer τ als mittlere Geschwindigkeit v der Phononen aufgefasst werden kann.
Die obere Gleichung besagt, dass für nichtmetallische Festkörper die Wärmeleitfähigkeit umso größer ist, je größer die massenspezifische Wärmekapazität und je größer die Dichte ist. Beide Größen können dabei zu einer neuen volumenspezifischen Wärmekapazität Cv zusammengefasst werden, die sich diesmal nicht auf die Masse bezieht, sondern auf das Volumen („Wärmekapazität pro Volumeneinheit“):
\begin{align}
\label{l}
& \boxed{\lambda = \tfrac{1}{3} \cdot C_v \cdot v \cdot l } ~~~~~\text{mit: }~~~ \boxed{C_v = c_v \cdot \rho} ~~~\text{Wärmekapazität pro Volumeneinheit}\\[5px]
\end{align}
Diese Gleichung gilt nicht nur zur Abschätzung der Wärmeleitfähigkeit in nicht-metallischen Festkörpern, sondern auch für ideale Gase!
Eine vertiefte Betrachtung der Wärmeleitfähigkeit von idealen Gasen wird im Artikel Wärmeleitfähigkeit von Gasen gegeben.
Die Wärmeleitfähigkeit von nichtmetallischen Feststoffen hängt gemäß oberer Formel von der volumenspezifischen Wärmekapazität ab. In diesem Fall ist es für eine hohe Wärmeleitfähigkeit von Vorteil, wenn der Stoff aus sehr vielen, aber leichten Teilchen aufgebaut ist. Die spezifische Wärmekapazität ist aber keine konstante Größe, sondern vor allem bei relativ niedrigen Temperaturen stark von der Temperatur abhängig. Auch die mittlere freie Weglänge ist stark temperaturabhängig, wohingegen die Geschwindigkeit der Phononen relativ unabhängig der Temperatur ist und deshalb als nahezu konstant betrachtet werden kann! Welche Auswirkungen damit auf die Wärmeleitfähigkeit von Nichtmetallen verbunden sind, soll im nächsten Abschnitt näher diskutiert werden.
Abhängigkeit der Wärmeleitfähigkeit von der Temperatur
Gitterschwingungen sind letztlich Schallwellen, die sich durch ein Material hindurch ausbreiten. Insofern breiten sich Phononen mit Schallgeschwindigkeit im Material aus. Dies Ausbreitungsgeschwindigkeit der Phononen kann in erster Näherung als relativ unabhängig der Temperatur betrachtet werden. Was die Temperaturabhängigkeit der Wärmeleitfähigkeit angeht, ist diese somit nur durch die spezifische Wärmekapazität und die mittlere freie Weglänge beeinflusst. Die unter Abbildung zeigt hierzu schematisch den Verlauf von mittlerer freier Weglänge, Wärmekapazität und hieraus resultierend die Wärmeleitfähigkeit in Abhängigkeit der Temperatur. Auf den Verlauf der einzelnen Größen wird im Folgenden näher eingegangen.
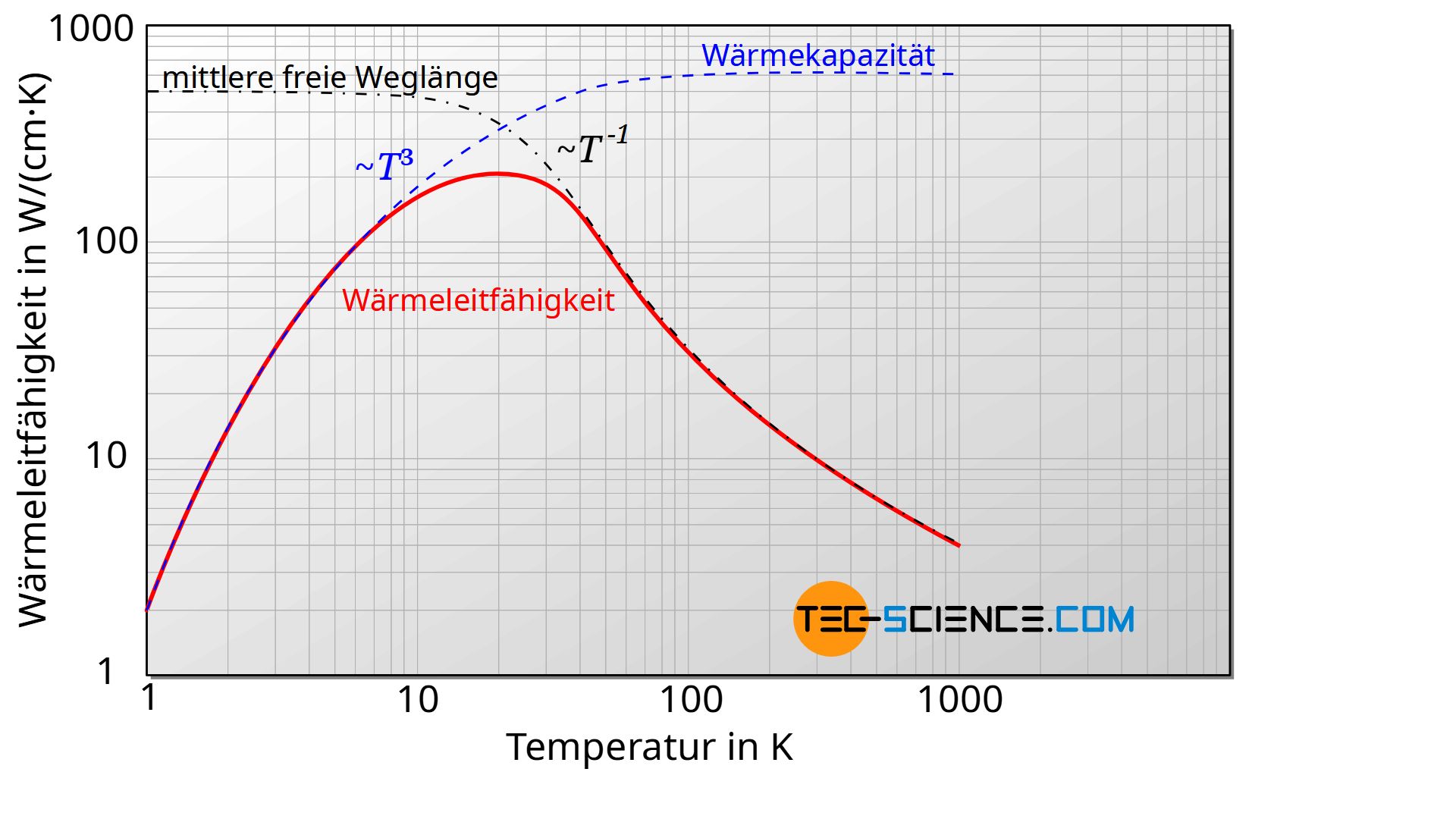
Sehr niedrige Temperaturen
Im Artikel Innere Energie & Wärmekapazität wurde das temperaturabhängige Verhalten der spezifischen Wärmekapazität von Feststoffen bereits ausführlicher behandelt. Dabei gilt für viele Feststoffe in sehr guter Näherung, dass die molare Wärmekapazität für sehr niedrige Temperaturen in der Nähe des absoluten Nullpunktes zunächst mit der dritten Potenz der Temperatur ansteigt. Nach einer Übergangsphase, charakterisiert durch die sogenannte Debye-Temperatur, steigt die Wärmekapazität dann nur noch geringfügig und kann als nahezu unabhängig der Temperatur betrachtet werden.
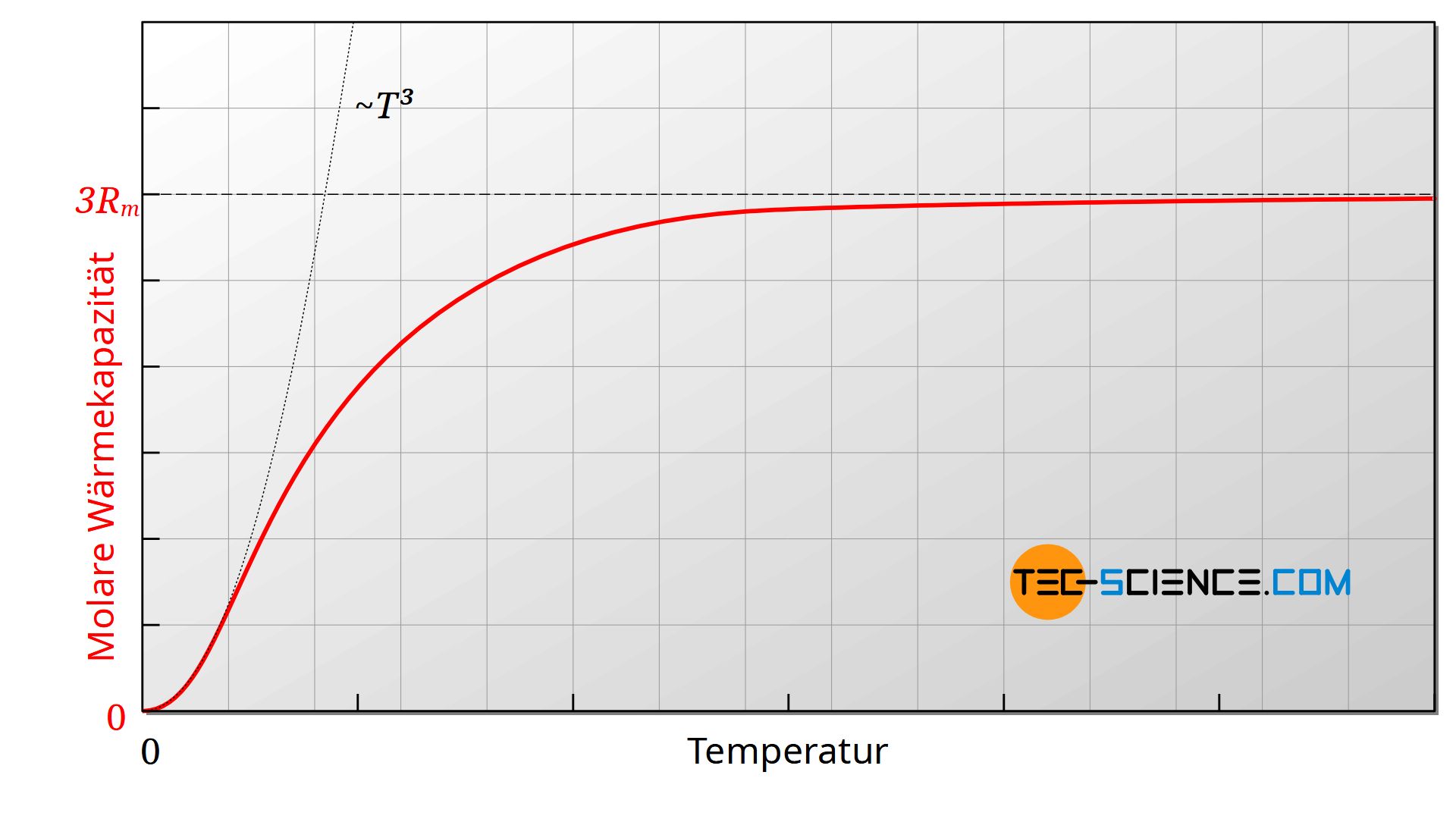
Anmerkung: Die Wärmeleitfähigkeit ist gemäß Gleichung (\ref{l}) durch die volumenspezifische Wärmekapazität ausgedrückt und nicht durch die molare Wärmekapazität. Dies ändert jedoch nichts an den qualitativen Aussagen. Die molare Wärmekapazität und die volumenspezifische Wärmekapazität können mithilfe konstanter Stoffgrößen ineinander umgerechnet werden. Es bleibt also dabei: Die Wärmekapazität (egal ob massenspezifisch, volumenspezifisch oder molar) ist für sehr niedrige Temperaturen proportional zur dritten Potenz der Temperatur und für hinreichend hohe Temperaturen relativ unabhängig der Temperatur.
Bei sehr geringen Temperaturen ist das Gitter nicht stark in Schwingung versetzt. Nur wenige Phononen wandern durch das Material. Die Phononen beeinflussen sich praktisch nicht gegenseitig. Hierdurch ist die mittlere freie Weglänge entsprechend groß und wird im Wesentlichen nur durch die Materialabmessungen oder die Fehlstellendichte begrenzt. Somit ist für niedrige Temperaturen auch die mittlere freie Weglänge relativ unabhängig der Temperatur, da sie eben nur durch die Dimension des Materials bestimmt ist.
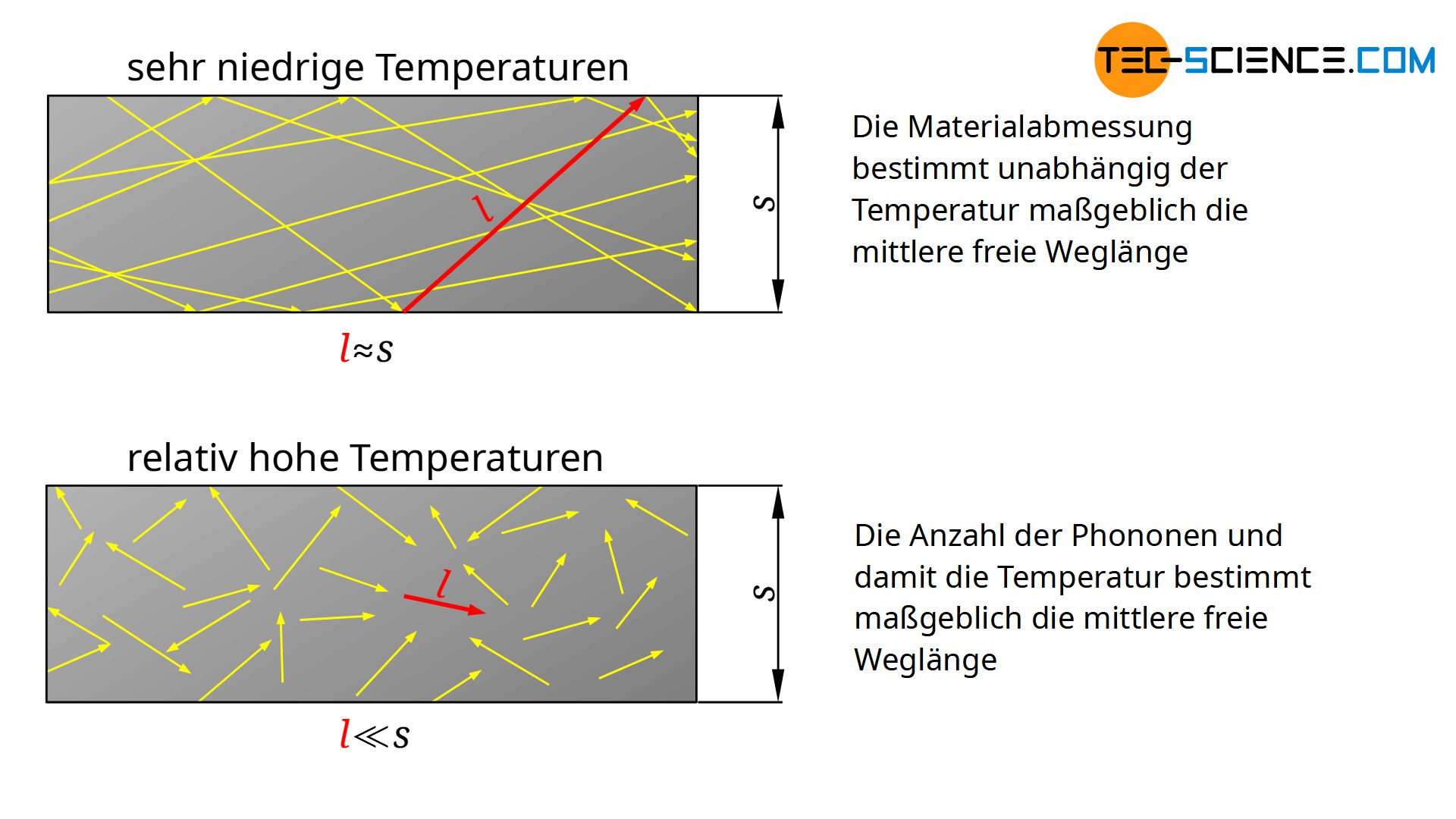
Die Tatsache, dass also für niedrige Temperaturen
- die Ausbreitungsgeschwindigkeit der Phononen ohnehin relativ unabhängig der Temperatur ist, und
- die mittlere freie Weglänge für sehr niedrige Temperaturen ebenfalls, aber
- die Wärmekapazität mit der dritten Potenz der Temperatur ansteigt,
führt dazu, dass die Wärmeleitfähigkeit ausgehend des absoluten Nullpunktes zunächst mit der dritten Potenz der Temperatur ansteigt.
Für geringe Temperaturen nimmt die Wärmeleitfähigkeit mit der dritten Potenz der Temperatur zu!
Relativ hohe Temperaturen
Gemäß des Gesetzes von Dulong-Petit nähert sich die molare Wärmekapazität Cm mit steigender Temperatur mehr und mehr dem dreifachen Wert der molaren Gaskonstante Rm an. Letztere bestimmt sich über die Avogadro-Konstante NA und die Boltzmann-Konstante kB:
\begin{align}
& \boxed{C_m \approx 3 \cdot R_m = 3 \cdot N_A \cdot k_B} ~~~\text{Gesetzes von Dulong-Petit} \\[5px]
\end{align}
Oberhalb der sogenannten Debye-Temperatur ist die Wärmekapazität deshalb kaum von der Temperatur abhängig. Sie ist insgesamt zwar größer als bei niedrigen Temperaturen, aber relativ konstant.
Bei hohen Temperaturen beeinflusst hauptsächlich die mittlere freie Weglänge die Wärmeleitfähigkeit (siehe Abbildung oben). Es kommt in diesem Fall zu relativ starken Gitterschwingungen. Die vielen und heftigen Gitterschwingungen beeinflussen sich dann sehr stark gegenseitig, d.h. Phononen werden an anderen Phononen gestreut. Die Phononen legen in diesem Fall nur kurze Wege zurück, bevor sie wieder an anderen Phononen gestreut werden.
Je höher also die Temperatur, desto mehr Phononen gibt es und umso geringere mittlere freie Weglängen ergeben sich. Bei einer doppelten Anzahl an Phononen hat sich die mittlere freie Weglänge gerade halbiert. Die Phononendichte ist oberhalb der Debye-Temperatur proportional zur Temperatur und die mittlere freie Weglänge damit umgekehrt proportional zur Temperatur.
Die Tatsache, dass also für hohe Temperaturen
- die Ausbreitungsgeschwindigkeit der Phononen weiterhin als konstant betrachtet werden kann, und
- die Wärmekapazität gemäß des Dulong-Petit Gesetztes ebenfalls unabhängig der Temperatur ist,
- aber die mittlere freie Weglänge sich umgekehrt proportional zur Temperatur verhält,
führt dazu, dass die Wärmeleitfähigkeit für hohe Temperaturen umgekehrt proportional mit der Temperatur sinkt.
Oberhalb der Debye-Temperatur nimmt in kristallinen nichtmetallischen Feststoffen die Wärmeleitfähigkeit umgekehrt proportional mit der Temperatur ab!
Geringe Temperaturen
Bei geringen Temperaturen, die nicht den Grenzfällen entsprechen wie sie oben beschrieben sind, ist die Wärmeleitung letztlich durch die mittlere freie Weglänge begrenzt, die sich durch die Streuung der Phononen an der Gitterstruktur bzw. an Fehlstellen ergibt (auch als Umklapp-Streuung, Umklappprozess oder U-Prozess bezeichnet). Dieser Übergangsbereich liegt meist im niedrigen zweistelligen Kelvinbereich.
Die Anzahl der Phononen die an einer solchen Umklapp-Streuung beteiligt sind, nimmt unterhalb der Debye-Temperatur exponentiell mit sinkender Temperatur ab. Dies hat dann schließlich die bereits erläuterte Vergrößerung der mittleren freien Weglänge zur Folge hat, bis bei hinreichend niedrigen Temperaturen die mittlere freie Weglänge schließlich nur durch die Probendimension oder die Fehlstellendichte begrenzt ist. Dies heißt aber auch, dass die Wärmeleitfähigkeit bei sehr niedrigen Temperaturen von der Probengeometrie abhängig ist! Breitere Proben mit einer entsprechend größeren mittleren freien Weglänge weisen höhere Wärmeleitfähigkeitswerte auf als schmälere Proben!
Amorphe Feststoffe
Auch bei amorphen Festkörpern findet man prinzipiell eine Abhängigkeit der Wärmeleitfähigkeit mit zunehmender Temperatur wieder. Die mittlere freie Weglänge ist dabei aber relativ unabhängig der Temperatur. Dies liegt daran, dass amorphe Festkörper keine regelmäßige Struktur aufweisen, sondern praktisch durchgehend Gitterstörungen aufweisen. Insofern liegt die mittlere freie Weglänge bei amorphen Festkörpern unabhängig der Temperatur stets in der Größenordnung der Atomabstände.
Dass sich auch bei amorphen Stoffen die Wärmeleitfähigkeit mit zunehmender Temperatur verändert, ist dabei maßgeblich auf die Änderung der Wärmekapazität zurückzuführen. Die Temperaturabhängigkeiten sind dabei jedoch etwas andere als bei kristallinen Stoffen, insbesondere steigt die Wärmekapazität nahe dem absoluten Nullpunkt nicht mehr mit der dritten Potenz der Temperatur an, sondern meist deutlich geringer.
Häufig ist bei amorphen Stoffen die Wärmekapazität größer als bei kristallinen Stoffen, die mittlere freie Weglänge jedoch deutlich geringer. Hierdurch ergeben sich insgesamt meist geringere Wärmeleitfähigkeitswerte im Vergleich zu kristallinen Stoffen.