Thermodynamic derivation of the Stefan-Boltzmann Law

In this article the Stefan-Boltzmann-Law is to be derived using the laws of thermodynamics.

Introduction

In this article, the Stefan-Boltzmann Law is to be derived with the laws of thermodynamics. In order to be able to do this, fundamental relationships must first be clarified.

Relationship between energy density and pressure

Kinetic theory of gases with classical particles

With the help of the kinetic theory of gases, the following relationship between the pressure of a gas p and the speed v of the particles contained therein was derived in the article Pressure and temperature:

\begin{align}
\label{p}
&\boxed{p = \frac{1}{3}\frac{N}{V}m\cdot \overline{v^2}} \\[5px]
\end{align}

Here N denotes the number of gas particles in a volume V and m refers to the mass of one particle (not the entire gas mass!). The speed refers to the root mean square speed.

In a classical view of ideal gases, in which the particle speeds are far below the speed of light, the mean kinetic energy of the particles can be described in very good approximation with ½⋅m⋅v² (Note that this formula only applies to non-relativistic mechanics!) The following relationship between the pressure and the mean energy of a particle becomes obvious:

\begin{align}
&p = \frac{2}{3} \cdot \frac{N}{V} \cdot \overbrace{\frac{1}{2} m \overline{v^2}}^{\overline{W_{kin}}} = \frac{2}{3} \cdot \frac{N}{V} \cdot \overline{W_{kin}} = \frac{2}{3} \cdot \frac{\overbrace{N \cdot \overline{W_{kin}}}^{\text{internal energy } U}}{V} = \frac{2}{3}\cdot \overbrace{\frac{U}{V}}^{\text{energy densitiy } u_v} = \frac{2}{3}\cdot u_v \\[5px]
&\boxed{p = \frac{2}{3} u_v} ~~~~~\text{only valid for a classical gas}
\end{align}

In the above derivation it was used that the product of the number of particles N and the mean kinetic energy of a particle corresponds to the total energy contained in the gas, i.e. the so-called internal energy U. The quotient of internal energy U and volume V can therefore be interpreted as (volumetric) energy density u_v (to avoid misunderstandings with the specific internal energy u as a mass-related quantity, a “v” is added to the energy density in the index).

Due to the fact that classical mechanics was used for the derivation under the assumption of the validity of W_kin=½⋅m⋅v², the obtained relationship between pressure and energy density applies only to classical ideal gases.

Kinetic theory of gases with relativistic particles (photons)

Due to the wave-particle duality, electromagnetic radiation can also be imagined as a beam of photons, as has already been done for the derivation of the radiation pressure. In this way, the radiation of a blackbody can now be described mathematically. In the article Blackbody radiation the realization of such a blackbody has already been explained in detail. For this purpose, a small hole is drilled into an object leading into a cavity.

All incident radiation is absorbed by the cavity, which also emits radiation itself. In thermal equilibrium, the emitted and absorbed radiation energy is the same, so that in principle a gas of photons is formed in the cavity. Instead of massive particles, in this case we are dealing with massless, relativistic photons. Here, too, a pressure p can be found in the cavity volume V due to the moving photons, the so-called radiation pressure.

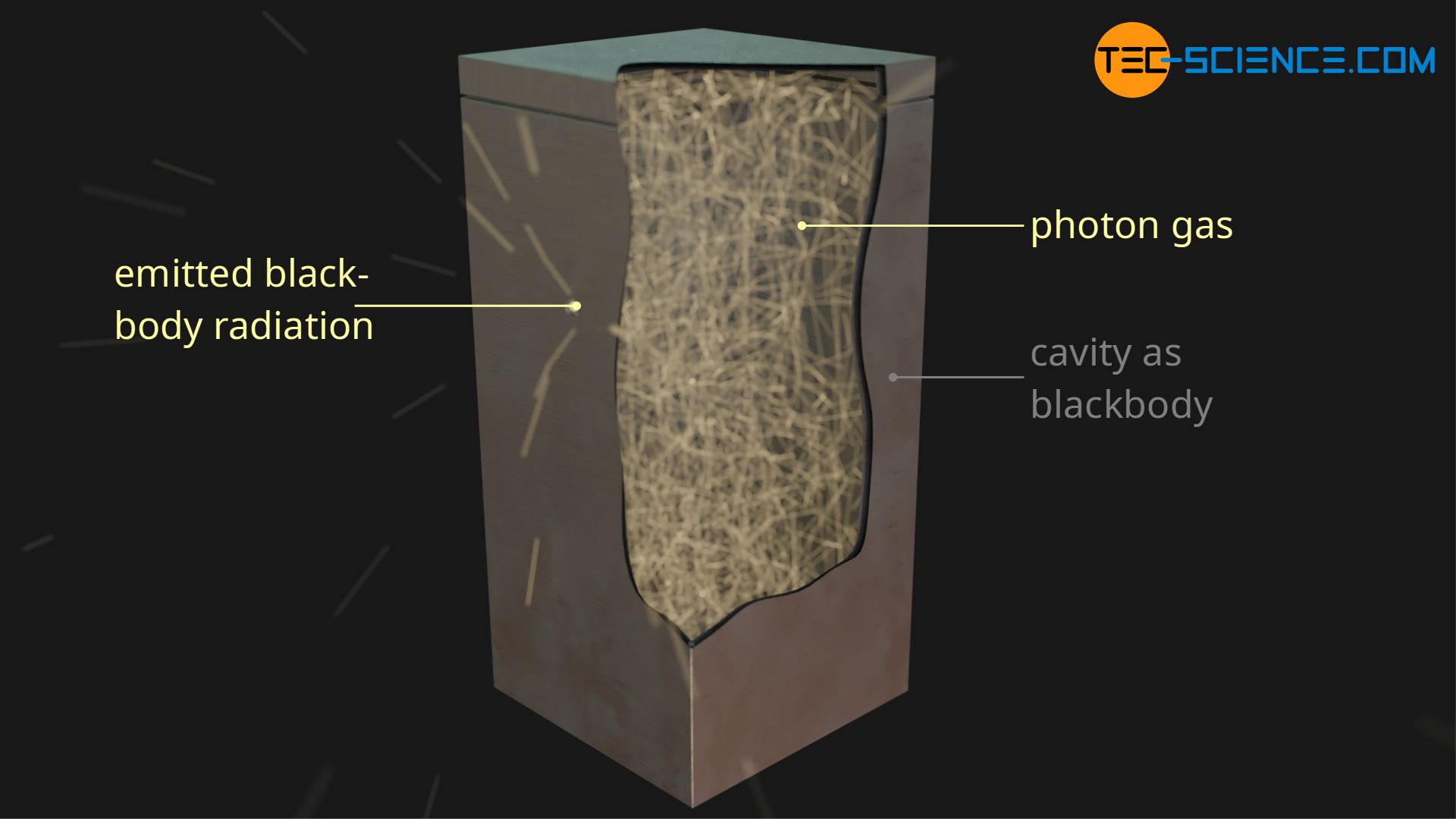
Equation (\ref{p}) can now also be used, it only has to be interpreted against the background of theory of relativity. For photons, the speed of the particles v corresponds to the speed of light c and the particle mass m must be considered as the relativistic mass m_rel. At this point it is not necessary to differentiate between the mean value of the speed squares \(\overline{c^2}\) and the speed square c², since in this case there is no classical speed distribution but all photons are travelling with the same speed of light. Both values are therefore identical.

\begin{align}
\label{pp}
&p = \frac{1}{3}\frac{N}{V}\cdot m_{rel} \cdot c^2 \\[5px]
\end{align}

Note that although photons do not have a rest mass, they do have a relativistic mass! For example, Einstein showed with his famous equation on energy-mass equivalence that every thing with energy can be assigned a corresponding (relativistic) mass m_rel:

\begin{align}
\label{e}
&\boxed{E =mc^2} ~~~~~\text{or}~~~~~ \boxed{W=m_{rel}\cdot c^2} \\[5px]
\end{align}

According to quantum mechanics, the energy of a photon results from the product of frequency f and Planck constant h, so that the relativistic mass can be determined from this:

\begin{align}
&W = h\cdot f \\[5px]
\end{align}

The product of the (relativistic) mass m (=m_rel) and the square of the speed of light c² contained in equation (\ref{pp}) corresponds to the energy of a photon W according to equation (\ref{e}). Thus the following relationship applies between the radiation pressure p of the photon gas and its energy density u_v:

\begin{align}
&p = \frac{1}{3}\frac{N}{V}\cdot \overbrace{ m_{rel}\cdot c^2}^{W}=\frac{1}{3}\frac{N}{V}\cdot W =\frac{1}{3}\frac{\overbrace{N\cdot W}^{\text{“internal” energy } U}}{V} =\frac{1}{3} \cdot \overbrace{\frac{U}{V}}^{\text{energy density }u_v} = \frac{1}{3} u_v \\[5px]
\label{h}
&\boxed{p = \frac{1}{3} u_v } ~~~~~\text{only valid for a photon gas (homogeneous radiation)}
\end{align}

The product of photon energy and number of photons corresponds to the total (internal) energy contained in the photon gas, i.e. the radiant energy (photon gas energy). The quotient of radiant energy and cavity volume can in turn be understood as the energy density of the photon gas or the energy density of the radiation.

The relationship between pressure and energy density of a classical gas thus differs by a factor of 2 from that of a relativistic photon gas.

Derivation from radiation pressure

The relationship between radiation pressure and energy density for a homogeneous photon gas can also be derived from the radiation pressure of a directed beam. In the article Radiation pressure it was shown that the radiation pressure p_beam, which a directed beam exerts on an object at complete reflection, corresponds to twice the value of the energy density:

\begin{align}
\label{s}
&\boxed{p_{beam} =2 \cdot u_v} ~~~~~\text{only valid for complete reflection of directed beams} \\[5px]
\end{align}

This equation does not contradict equation (\ref{h})! Because equation (\ref{s}) is only valid for directed radiation, i.e. when all photons move in the same direction and hit a boundary surface. In the present case of cavity radiation, however, it is a matter of radiation that is permanently reflected, absorbed and emitted inside, i.e. the photons all move in completely random directions; it is actually a photon gas.

In order to make a completely random photon motion out of a directed photon beam, all photons contained in it would suddenly have to move in different directions. Assuming a homogeneous statistical distribution, one sixth of the photons would move upwards, one sixth downwards, one sixth to the left and one sixth to the right, and one sixth to the rear, and finally one sixth of the photons would move forwards towards the boundary surface under consideration, on which a pressure would be exerted.

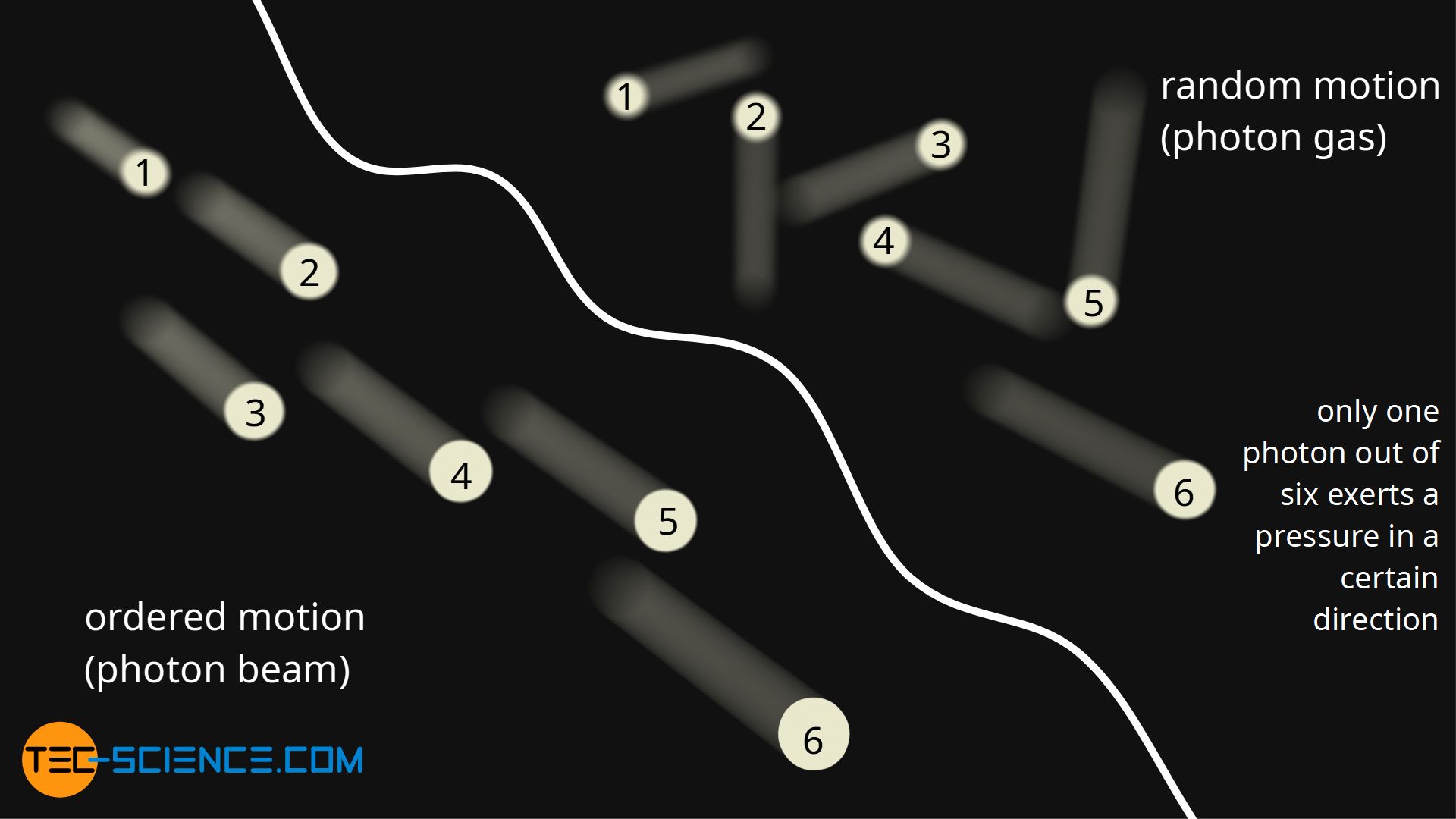
At the same energy density (photon density), the pressure of a homogeneous photon gas is thus one sixth lower than that of a directed photon beam, since only one sixth of the photons effectively collide with the boundary surface. Thus, for a homogeneous photon gas, one obtains the same relationship:

\begin{align}
& p = \frac{1}{6} \cdot p_{beam} = \frac{1}{6} \cdot 2 \cdot u_v= \frac{1}{3} \cdot u_v \\[5px]
\end{align}

One could now argue at this point that the cavity radiation is not based on a complete reflection and thus equation (\ref{s}) is not valid at all. Rather, a blackbody or a cavity radiation is a complete absorption of the radiation. This is correct, but in thermal equilibrium exactly the same number of photons are absorbed as emitted. This is where the thermodynamic equilibrium comes into being.

Kinematically speaking, a reflection is nothing more than an absorption (“impact”) with subsequent emission (“rebound”). Only because absorption and emission do not take place at identical times in the case of cavity radiation, they are essentially identical to reflection, in which both processes in principle take place immediately one after the other. For this reason, a completely reflective behavior must be assumed for cavity radiation in thermodynamic equilibrium!

Relationship between a change in volume and the change in photon gas energy

As the experimental study of blackbody radiation has already shown, the energy of the radiation emitted depends only on the temperature. The energy density is therefore only a function of the temperature. At constant temperature and thus constant energy density u_v, an increase of the cavity volume by dV means a corresponding increase of the photon gas energy dU:

\begin{align}
& U(T,V) = u_v(T) \cdot V \\[5px]
& \frac{\text{d}U(T,V)}{\text{d}V} =\frac{\text{d}(u_v(T) \cdot V )}{\text{d}V} = \overbrace{\underbrace{\frac{\partial{u_v(T)}}{\partial{V}}}_{=0} \cdot V +\underbrace{\frac{\partial{V} }{\partial{V}}}_{=1} \cdot u_v(T)}^{\text{product rule}} = u_v(T) = u_v \\[5px]
\label{t}
&\boxed{\left(\frac{\partial{U}}{\partial{V}}\right)_T = u_v = 3p} \\[5px]
\end{align}

Note that the (partial) derivation of the energy density with respect to the volume equals to zero, since the energy density is not a function of the volume. With respect to the variable V, this is the derivation of a constant. In the last step it was used that the energy density u_v corresponds to three times the value of the pressure p [see equation (\ref{h})].

The fact that the photon gas energy increases at a constant energy density to the same extent as the volume also becomes clear, because a constant energy density also means a constant photon density. If one increases the volume of the cavity, then with constant photon density there are now more photons in it (the cavity then emits more photons until the thermal equilibrium is restored). Since each photon is associated with a certain energy, the total energy contained in the volume has also increased.

First law of thermodynamics

Since the photon gas is considered analogous to a classical ideal gas, the first law of thermodynamics can also be applied at this point. In differential form, it is represented as follows (in which S denotes the entropy):

\begin{align}
&\boxed{\text{d}U = T \cdot \text{d}S – p \cdot \text{d}V } ~~~~~\text{First law of thermodynamics} \\[5px]
\end{align}

If this equation is divided by dV, the following relationship is obtained at constant temperature:

\begin{align}
\label{ss}
& \left(\frac{\partial{U}}{\partial{V}}\right)_T = T \left(\frac{\partial{S}}{\partial{V}}\right)_T – p \\[5px]
\end{align}

Without going deeper into the derivation of the so-called Maxwell relations of thermodynamics, these provide another important relationship at this point: A change in entropy and a change in volume at constant temperature are in the same relationship as a change in pressure and a change in temperature at constant volume. Mathematically this is expressed as follows:

\begin{align}
&\boxed{\left(\frac{\partial{S}}{\partial{V}}\right)_T = \left(\frac{\partial{p}}{\partial{T}}\right)_V} ~~~~~\text{Maxwell relation} \\[5px]
\end{align}

This Maxwell relation can now be used in equation (\ref{ss}):

\begin{align}
\label{x}
& \left(\frac{\partial{U}}{\partial{V}}\right)_T = T \left(\frac{\partial{p}}{\partial{T}}\right)_V – p \\[5px]
\end{align}

According to equation (\ref{t}) the term (∂U/∂V)_T can be replaced by the energy density u_v. In addition, the pressure p according to the equation (\ref{h}) corresponds to just one third of the energy density:

\begin{align}
u_v &= T \left(\frac{\partial{\frac{1}{3}u_v}}{\partial{T}}\right)_V – \frac{1}{3} u_v \\[5px]
u_v &= \frac{1}{3} T \left(\frac{\partial{u_v}}{\partial{T}}\right)_V – \frac{1}{3} u_v \\[5px]
3 u_v &= T \left(\frac{\partial{u_v}}{\partial{T}}\right)_V – u_v \\[5px]
\end{align}

Since the energy density is only a function of temperature, the partial derivative with respect to the temperature can be expressed as an ordinary derivative. After separation of variables (Fourier method) we obtain:

\begin{align}
3 u_v &= T \frac{\text{d}u_v}{\text{d}T} – u_v \\[5px]
4 u_v &= T \frac{\text{d}u_v}{\text{d}T} \\[5px]
\frac{\text{d}u_v}{u_v} &=4 \frac{\text{d}T}{T} \\[5px]
\end{align}

Both sides of the equation can now be integrated, whereby constants of integration must be taken into account when calculating the primitive function, which are summarized in the constant a (in this case, a generally stands for a constant, not for a special value!):

\begin{align}
\int \frac{\text{d}u_v}{u_v} &= \int 4 \frac{\text{d}T}{T} \\[5px]
\ln{u_v} &= 4 \cdot \ln{T} + a\\[5px]
e^{\ln{u_v}} &= e^{4 \cdot \ln{T}+a} \\[5px]
e^{\ln{u_v}} &= e^{4 \cdot \ln{T}} \cdot e^{a} \\[5px]
e^{\ln{u_v}} &= \left(e^{\ln{T}}\right)^4 \cdot a \\[5px]
&\underline{u_v = a \cdot T^4} \\[5px]
\end{align}

The energy density u_v is thus proportional to the fourth power of the absolute temperature T. A volume V filled with photons (e.g. the volume of the considered cavity), which are emitted by a blackbody at the temperature T, contains the following total energy U:

\begin{align}
&U = u_v \cdot V = a \cdot T^4 \cdot V \\[5px]
\label{st}
&\boxed{U = a \cdot T^4 \cdot V} \\[5px]
\end{align}

The constant a could now be determined experimentally. Usually, however, it is not the energy of a photon gas that is of interest but the power with which the body emits the photons.

Radiant power

In the following, a blackbody with a surface area A is considered, which is in thermodynamic equilibrium at the temperature T. This black body emits photons that move away from the surface at the speed of light c (in the case of a hollow body into the cavity and then through the hole into the environment, or in the case of a solid body directly into the environment). Within the infinitesimal time dt these photons cover a certain distance ds:

\begin{align}
& \text{d}s = c \cdot \text{d}t \\[5px]
\end{align}

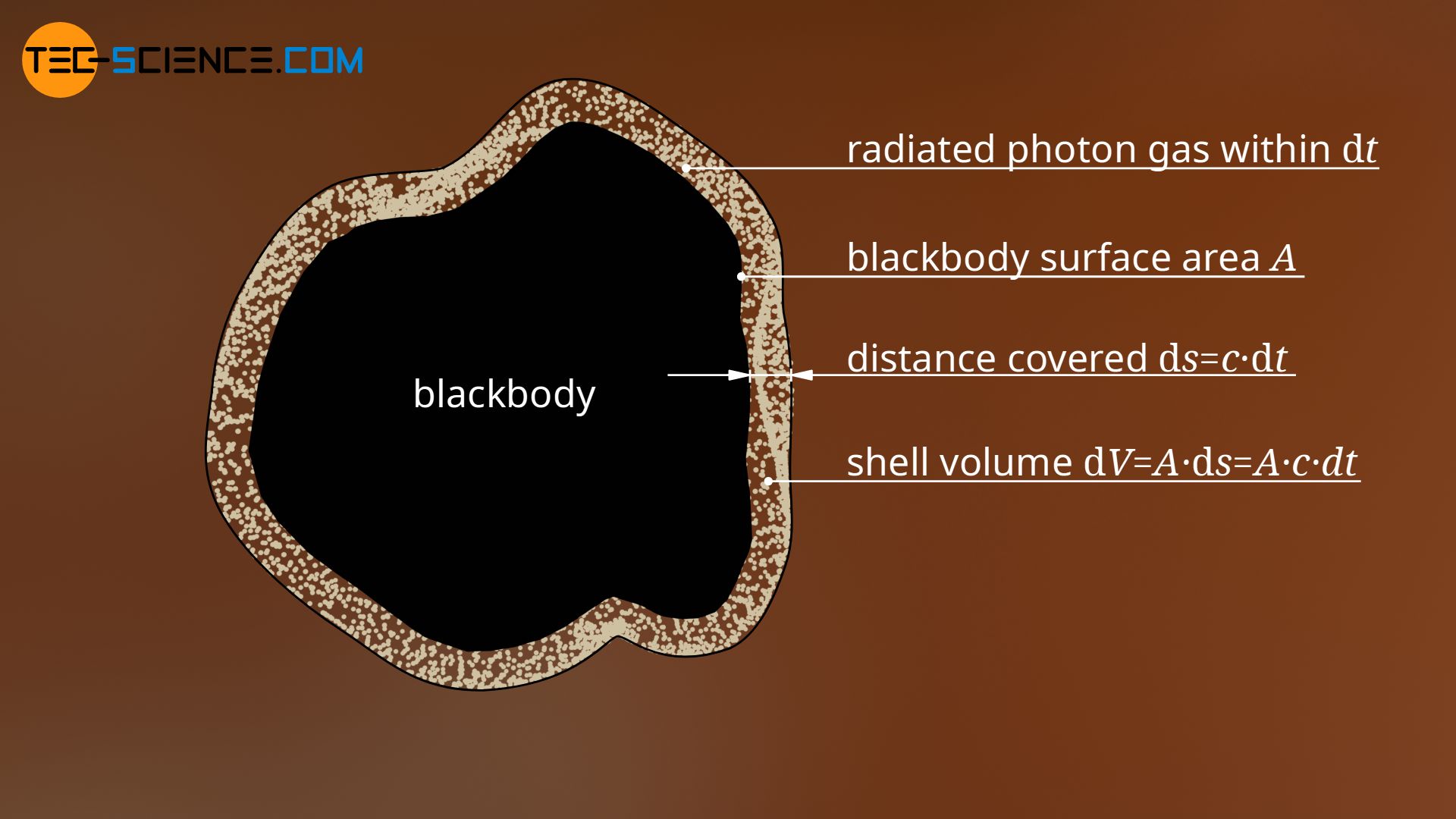
Since the photons are emitted from the surface area A, they occupy a certain shell volume around the blackbody within the time dt. Due to the infinitesimal distance, the volume dV of this emitted photon shell results from the product of base area A and height ds:

\begin{align}
& \text{d}V = A \cdot \text{d}s = A \cdot c \cdot \text{d}t \\[5px]
\end{align}

At a given temperature T the energy dU contained in the emitted photon volume dV is given by equation (\ref{st}).

\begin{align}
&\text{d}U = a \cdot T^4 \cdot \text{d}V= a \cdot T^4 \cdot A \cdot c \cdot \text{d}t \\[5px]
\end{align}

Within the time dt the blackbody radiates the energy dU. From this the radiant power Φ can be determined as the emitted radiant energy per unit time:

\begin{align}
\require{cancel}
&\Phi =\frac{\text{d}U}{\text{d}t} = \frac{a \cdot T^4 \cdot A \cdot c \cdot \bcancel{\text{d}t} }{\bcancel{\text{d}t}} =\underbrace{a\cdot c}_{\sigma} \cdot A \cdot T^4 \\[5px]
\end{align}

The constant a and the constant speed of light c can be combined to a new constant, the so-called Stefan-Boltzmann constant σ (not to be confused with the Boltzmann constant k_B!). Thus the radiant power of a black body in thermodynamic equilibrium at a given temperature T results from the following formula:

\begin{align}
\label{bb}
&\boxed{\Phi = \sigma \cdot A \cdot T^4} ~~~~~ \sigma = 5,670 \cdot 10^{-8} \frac{\text{W}}{\text{m²K}^4} \\[5px]
\end{align}

This law was experimentally derived by the physicist Josef Stefan and later mathematically derived by Ludwig Boltzmann. This law is therefore called the Stefan-Boltzmann Law.

If the radiant power Φ at this point is related to the surface area A of the blackbody, then the intensity I is obtained:

\begin{align}
&I=\frac{\Phi}{A} = \frac{\sigma \cdot A \cdot T^4}{A} = \sigma \cdot T^4\\[5px]
&\boxed{I = \sigma \cdot T^4 } \\[5px]
\end{align}

The Stefan-Boltzmann constant σ, which was initially determined empirically by experiments, is a fundamental physical constant that could actually only be derived from other fundamental constants by quantum mechanics:

\begin{align}
&\boxed{\sigma = \frac{2 \pi^5k_B^4}{15h^3c^2} } \\[5px]
\end{align}

As already explained at the beginning of this article, Blackbodies only exist in the ideal. In reality, therefore, bodies do not radiate with the intensity of a black body but with lower power. This is expressed by the emissivity ε<1:

\begin{align}
&I=\varepsilon \cdot \sigma \cdot T^4\\[5px]
\end{align}