Learn more in this article about the differences and importance of thermal conductivity, thermal diffusivity, heat transfer coefficient, thermal transmittance and thermal resistance, etc.
Thermal conductivity
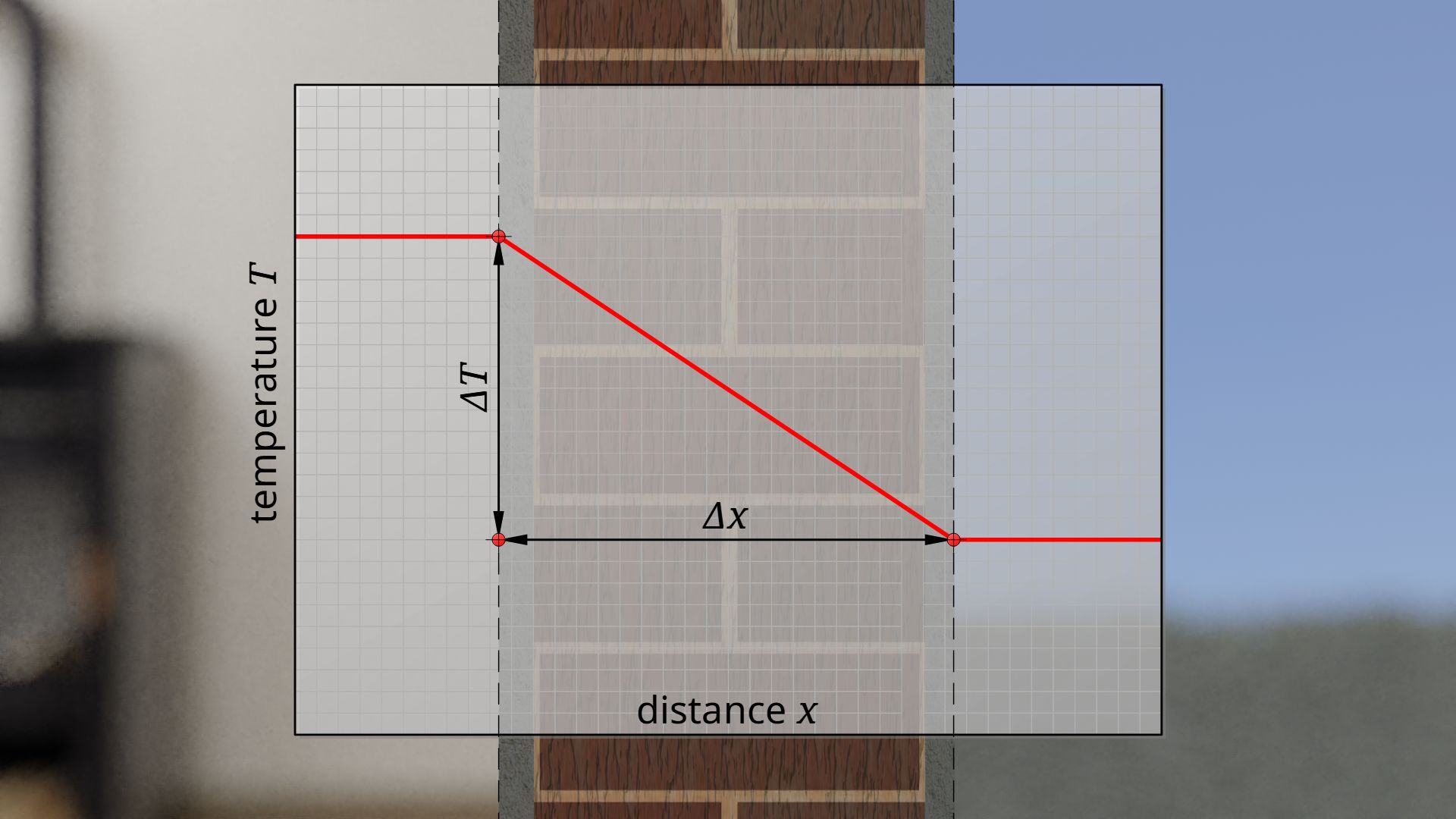
Thermal conductivity \(\lambda\) describes the heat transfer in the steady state by thermal conduction due to a temperature gradient \(\frac{\delta T}{\delta x}\). Fourier’s law applies to the heat flux \(\dot q\) (rate of heat flow per unit area):
\begin{align}
&\boxed{\dot q= \lambda \cdot \frac{\Delta T}{\Delta x}}~~~~~\text{Fourier’s law} \\[5px]
\end{align}
More information about thermal conductivity can be found in the article Thermal conductivity (Fourier’s law).
Thermal transmittance and thermal resistance of conduction
If the thermal conductivity \(\lambda\) is related to the thickness of the object \(\Delta x\) through which the heat is transferred, the thermal transmittance of conduction \(\Lambda\) is obtained:
\begin{align}
&\dot q= \underbrace{\frac{\lambda}{\Delta x}}_{\text{thermal transmittance}\\{\text{of conduction }\Lambda}} \cdot \Delta T \\[5px]
\end{align}
Fourier’s law is in this case is:
\begin{align}
&\boxed{\dot q= \Lambda \cdot \Delta T}~~~\text{where }~~ \boxed{\Lambda=\frac{\lambda}{\Delta x}}~~\text{thermal transmittance of conduction} \\[5px]
\end{align}
While the thermal conductivity is a characteristic quantity which only depends on the material (material-dependent quantity), the thermal transmittance depends on the size of the object, because it takes into account the actual thickness of the object (component-dependent quantity)!
The reciprocal of the thermal transmittance (of conduction) is called thermal resistance (of conduction) \(R\):
\begin{align}
&R:=\frac{1}{\Lambda} \\[5px]
&\boxed{R=\frac{\Delta x}{\lambda}} ~~~\text{thermal resistance of conduction} \\[5px]
\end{align}
As a component-dependent quantity, the thermal resistance of conduction describes the insulating effect of a component with regard to thermal conduction!
Thermal diffusivity
The thermal diffusivity \(a\) is related to the thermal conductivity. The thermal diffusivity is determined by the density \(\rho\) and the specific heat capacity of the material \(c\):
\begin{align}
&\boxed{a=\frac{\lambda}{\rho \cdot c}} ~~~~~\text{thermal diffusivity}\\[5px]
\end{align}
In contrast to thermal conductivity (steady state of thermal conduction), thermal diffusivity describes the heat transfer for thermal conduction in an unsteady state, i.e. the temporal propagation of temperature inside an object.
The thermal diffusivity \(a\) links the local change of the temperature gradient (\(\frac{\partial^2 T}{\partial x^2}\)) with the resulting temporal change of the temperature (\(\frac{\partial T}{\partial t}\)). The mathematical equation which describes this relationship is called the heat equation (diffusion equation):
\begin{align}
& \boxed{\frac{\partial T}{\partial t} = a \cdot \frac{\partial^2 T}{\partial x^2}}~~~\text{one-dimensional heat equation} \\[5px]
\end{align}
With the heat equation the temporal temperature propagation along a rod can be determined, for example.
Heat transfer coefficient and thermal resistance of convection
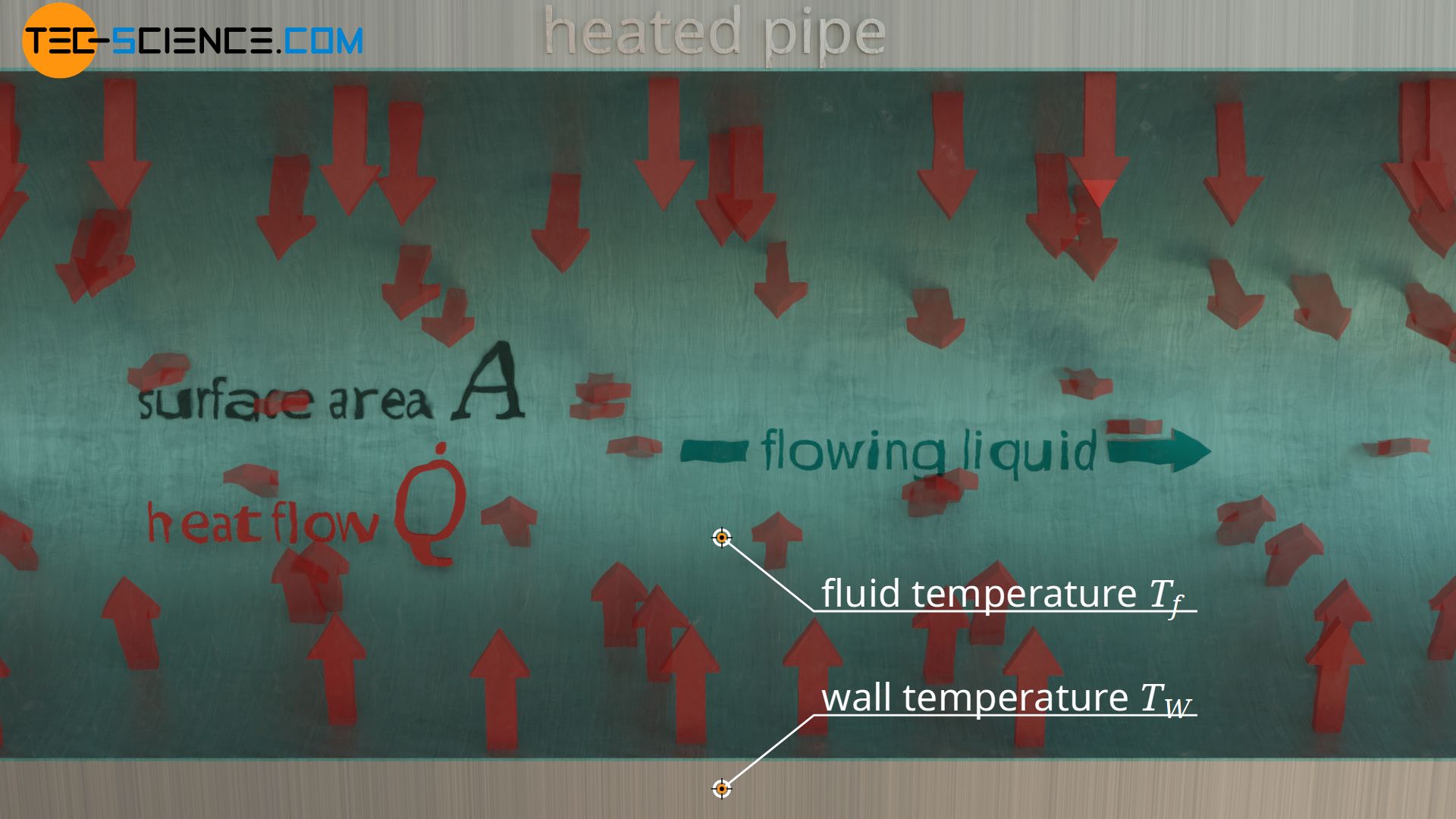
The heat transfer coefficient \(\alpha\) describes the heat transfer by thermal convection between a fluid (gas or liquid) and a solid due to a temperature difference between these mediums. Such heat transport is of great importance, for example, in a pipe where water flows through. Between water and pipe wall heat is transferred by convection, if for example the pipe is warmer than the water. The heat flux \(\dot q\) at the interface between solid (“wall”) and fluid can be calculated using the following formula:
\begin{align}
&\boxed{\dot q = \alpha \cdot (T_w-T_f)} \\[5px]
\end{align}
In this formula, the temperature of the fluid is denoted by \(T_f\) and the the temperature directly at the surface of the solid wall is denoted by \(T_w\). More information about the heat transfer coefficient can be found in the article Heat transfer coefficient for thermal convection.
The reciprocal of the heat transfer coefficient is called thermal resistance of convection heat transfer resistance \(R_\text{s}\):
\begin{align}
\label{rk}
&\boxed{R_\text{s} =\frac{1}{\alpha}} ~~~\text{thermal resistance of convection} \\[5px]
\end{align}
As a component-dependent quantity, the thermal resistance of convection describes the insulating effect of an object with regard to the thermal convection!
Thermal transmittance (U-value)
The (overall) thermal transmittance \(U\), also called U-value or U-factor, describes the heat transfer between two fluids separated by a solid. The heat flux \(\dot q\) through the solid depends on the temperature difference \(\Delta T\) of the fluids:
\begin{align}
&\boxed{\dot q = U \cdot \Delta T}\\[5px]
\end{align}
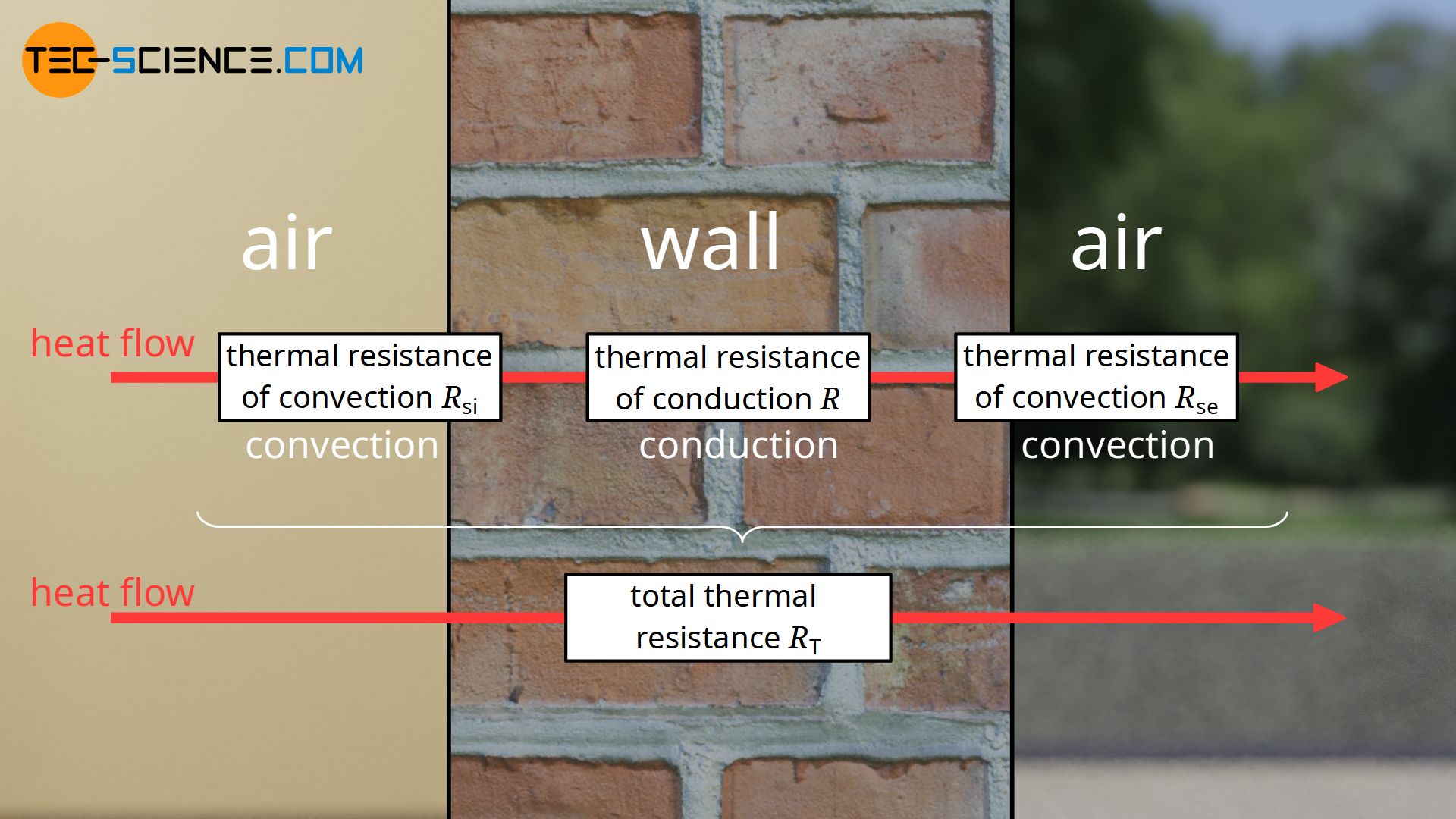
The U-value plays a major role in the building engineering, where, for example, a building wall separates the air inside the building from the air outside. Two heat transfer mechanisms play a special role, whereby the entire heat transfer can be divided into three steps:
- thermal convection from the fluid to one side of the separating object (“interior”)
→ thermal resistance of convection \(R_\text{si}\) - thermal conduction through the separating object
→ thermal resistance of conduction \(R\) - thermal convection from the opposite side of the separating object (“exterior”) onto the fluid
→ thermal resistance of convection \(R_\text{se}\)
The sum of the individual thermal resistances finally results in the total thermal resistance \(R_\text{T}\) through the component (analogous to electrical resistances):
\begin{align}
&\boxed{R_\text{T} =R_\text{si} + R + R_\text{se}} ~~~\text{total thermal resistance}\\[5px]
\end{align}
The total thermal resistance thus describes the insulating effect of a component which separates two fluids (e.g. air). The reciprocal value of the total thermal resistance finally corresponds to the U-value (overall thermal transmittance):
\begin{align}
&\boxed{U = \frac{1}{R_\text{T}} =\frac{1}{R_\text{si} + R + R_\text{se}}} ~~~\text{U-value}\\[5px]
\end{align}
Summary
| quantity | description of … | Note |
|---|---|---|
| thermal conductivity \(\lambda\) | thermal conduction in the steady state | material property |
| thermal transmittance of conduction \(\Lambda\) | thermal conduction in the steady state | component property |
| thermal resistance of conduction \(R\) | insulation effect for thermal conduction | reciprocal value of thermal transmittance of conduction |
| thermal diffusivity \(a\) | temperature propagation by heat conduction (unsteady state) | see heat equation (diffusion equation) |
| heat transfer coefficient \(\alpha\) | Thermal convection between fluid and solid | – |
| thermal resistance of convection \(R_\text{s}\) | insulation effect for thermal convection | reciprocal value of heat transfer coefficient |
| thermal transmittance \(U\) (U-value) | heat transfer between two fluids separated by a solid | simultaneous presence of convection and conduction |
| overall thermal resistance \(R_\text{T}\) | insulation effect for heat transfer between two fluids separated by a solid | reciprocal value of thermal transmittance (U-value) |