Stokes’ law of friction describes the drag force acting on a spherical body around which a laminar flow passes.
Flow resistance and drag coefficient
When a fluid (liquid or gas) flows around a body, the fluid exerts a frictional force on the body. In principle, it does not matter whether the body is at rest and the fluid flows around it, or vice versa: the fluid is at rest and the body moves through the fluid. A body that moves relative to a surrounding fluid thus experiences a frictional force. This frictional force is also called flow drag.
In general, the drag force Fd of a body can be calculated with the following formula:
\begin{align}
\label{f}
&\boxed{F_\text{d} =\frac{1}{2}~\rho~v_\infty^2~A~ c_\text{d}} \\[5px]
\end{align}
In this formula ϱ denotes the density of the fluid, i.e. the denser the fluid, the greater the drag. An object moving through air will therefore experience less resistance than one moving through water.
Furthermore, the drag depends on the speed v∞ with which the object moves relative to the surrounding fluid or on the speed with which the fluid flows around the body. In the latter case, the velocity refers to the velocity of the undisturbed flow (freestream), i.e. the velocity at a sufficiently large distance from the body around which the fluid flows. The drag is proportional to the square of the flow velocity. A speed twice as high therefore means a fourfold increase in drag force.
The area A of the body pointing in flow direction (projected area) also has a decisive influence on the drag. One can imagine that the object is illuminated by a lamp in the flow direction. The resulting shadow cast on a wall behind the object would then correspond to the projected area A.

The projected area only describes the size of the body surface exposed to the flow, but not its exact shape. However, the shape is of decisive importance when it comes to flow resistance. For example, the drag of a hollow hemisphere is almost four times greater when the flow is against the concave side than when the flow is against the convex side of the hemisphere, although the projected area is obviously the same in both cases. This influence of the body shape on the drag is expressed by a dimensionless drag coefficient cd.
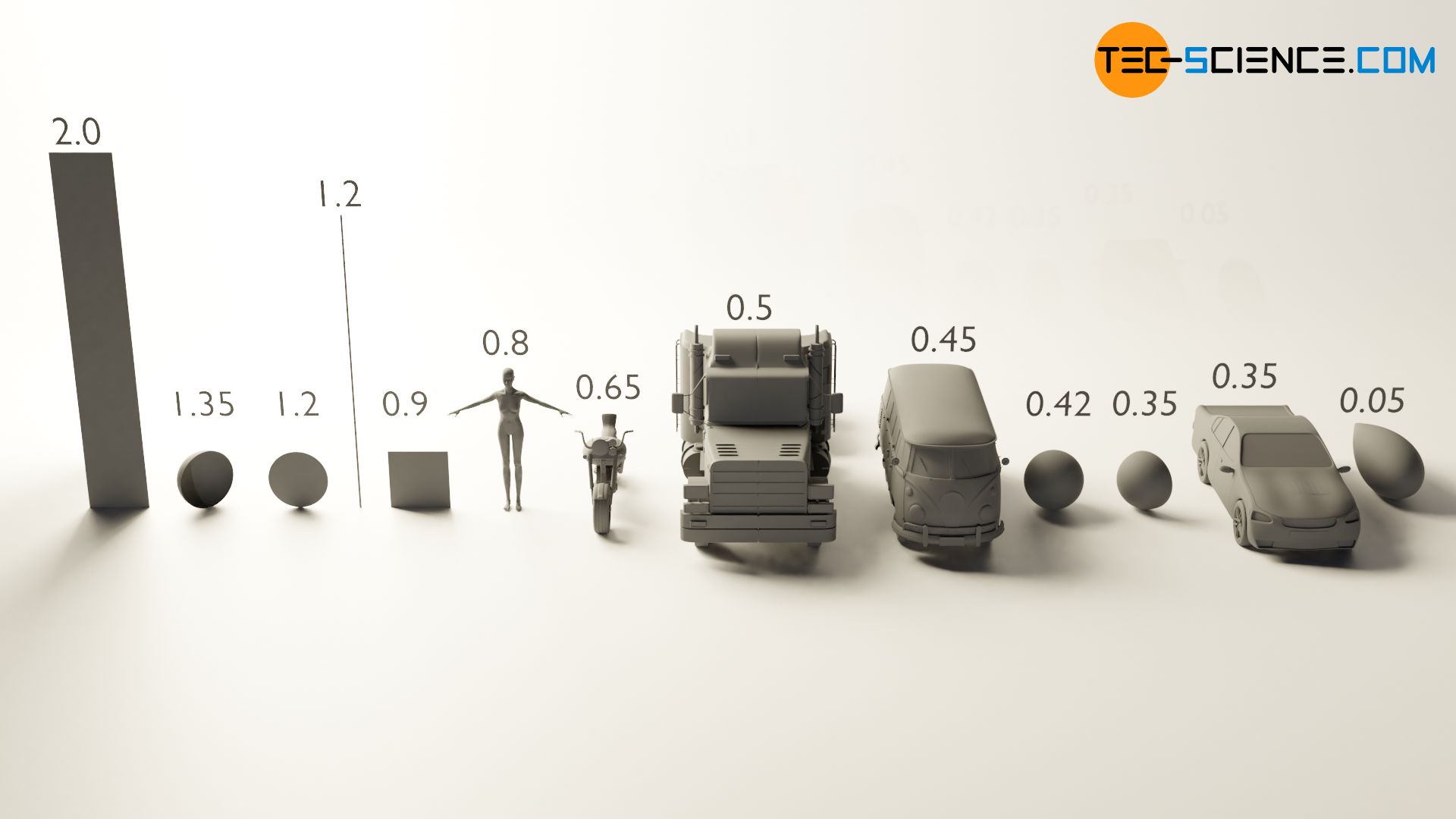
Drag coefficient of spherical bodies in laminar flows
The drag coefficients of geometrically complex objects are usually determined by experiments in wind tunnels or water channels. For relatively simple geometric shapes such as smooth spheres, however, scientists have tried to calculate the drag coefficients under simplified conditions. The scientist Kaskas developed the following formula for the approximate calculation of the drag coefficient of spherical bodies in laminar flows:
\begin{align}
&\boxed{c_\text{d} = \frac{24}{Re} +\frac{4}{\sqrt{Re}}+0.4}~~Re<2\cdot 10^5 \\[5px]
\end{align}
In this equation, Re denotes the dimensionless flow velocity in terms of the Reynolds number. For spherical bodies, the Reynolds number is determined by the flow velocity v∞, the density ϱ of the fluid and its dynamic viscosity η and the diameter d of the sphere as the characteristic length:
\begin{align}
&\boxed{Re = \frac{v_\infty~d~\rho}{\eta}} \\[5px]
\end{align}
Stokes’ law of friction for small Reynolds numbers
Despite laminar flow, flow separation (boundary layer separation) and vortices usually form behind a spherical body, which at high Reynolds numbers result in a turbulent wake. The figure below shows a schematic streamline image of a laminar flow around a ball with turbulent wake.

Only at low flow velocities, where the Reynolds number is less than 1, a symmetrical streamline pattern can be assumed. Such a flow is also called a creeping flow and is completely attached to the sphere and does not form any vortices on the downstream side. In this case, the scientist Stokes was able to derive the following formula for determining the drag coefficient from the Navier-Stokes equations:
\begin{align}
&\boxed{c_\text{d} = \frac{24}{Re} }~~Re<1 \\[5px]
\end{align}

The formula of Kaskas does not contradict the formula of Stokes. For small Reynolds numbers the last two terms in the formula of Kaskas are negligible compared to the first term. Thus the value from the formula of Kaskas approaches more and more the drag value, which is obtained from the formula of Stokes. If Stokes’ formula ist used in equation (\ref{f}), the following relationship results for the drag force of a completely laminar flow around a sphere:
\begin{align}
\require{cancel}
&F_\text{d} =\frac{1}{2}~\rho~v_\infty^2~\color{red}{A}~ \color{blue}{c_\text{d}} \\[5px]
&F_\text{d} =\frac{1}{2}~\rho~v_\infty^2~\color{red}{\frac{\pi}{4}d^2}~ \color{blue}{\frac{24}{Re}} \\[5px]
&F_\text{d} =\frac{1}{2}~\bcancel{\rho}~v_\infty^\bcancel{2}~\frac{\pi}{4}d^\bcancel{2}~ \frac{24~\eta}{\bcancel{v_\infty}~\bcancel{d}~\bcancel{\rho}} \\[5px]
&F_\text{d} =\frac{1}{2}~v_\infty~\frac{\pi}{4}d~ 24~\eta \\[5px]
&F_\text{d} =3\pi~\eta~v_\infty~d \\[5px]
&\boxed{F_\text{d} =6\pi~\eta~v_\infty~r} ~~~\text{Stokes’ law of friction}\\[5px]
\end{align}
The flow resistance of a spherical body caused by a laminar flow depends on the viscosity of the fluid η, the flow velocity v∞ and the radius r of the sphere. Note that the flow velocity no longer influences the drag with the square of the velocity, but only proportionally!
Stokes’ law of friction for laminar flows around spherical bodies states that the drag force is proportional to the viscosity of the fluid, the flow velocity and the radius of the sphere!
The relationship between the viscosity of a fluid and the drag caused on a sphere is used, for example, in so-called falling-sphere viscometers, in order to draw conclusions about the viscosity of a fluid based on the sinking speed of a sphere.







