Das Stokes’sche Reibungsgesetz beschreibt den Strömungswiderstand auf einen kugelförmigen Körper, der laminar umströmt wird.
Strömungswiderstand und Widerstandsbeiwert
Wird ein Körper von einem Fluid (Flüssigkeit oder Gas) umströmt, so reibt das umströmende Fluid am Gegenstand. Dabei spielt es im Prinzip keine Rolle ob der Körper ruht und vom Fluid umströmt wird, oder umgekehrt, das Fluid ruht und der Körper sich durch das Fluid bewegt. Ein Körper, der sich relativ zu einem umgebenden Fluid bewegt, erfährt somit eine Reibungskraft. Diese Reibungskraft wird auch als Strömungswiderstand bezeichnet.
Im Allgemeinen lässt sich die Widerstandskraft Fw eines Körpers mit folgender Formel berechnen:
\begin{align}
\label{f}
&\boxed{F_\text{w} =\frac{1}{2}~\rho~v_\infty^2~A~ c_\text{w}} \\[5px]
\end{align}
Darin bezeichnet ϱ die Dichte des Fluids, d.h. umso dichter das Fluid, desto größer der Strömungswiderstand. Ein Gegenstand, der sich durch Luft bewegt, wird somit eine geringere Widerstandskraft erfahren als wenn sich dieser durch Wasser bewegt.
Zudem hängt der Strömungswiderstand von der Geschwindigkeit v∞ ab, mit der sich der Gegenstand relativ zum umgebenden Fluid bewegt bzw. von der Geschwindigkeit, mit der Körper vom Fluid umströmt wird. Im letzteren Fall bezieht sich die Geschwindigkeit auf die Geschwindigkeit der ungestörten Anströmung, d.h. auf die Geschwindigkeit in hinreichend großem Abstand zum umströmten Körper. Die Strömungsgeschwindigkeit hat dabei einen quadratischen Einfluss auf die Widerstandskraft. Eine doppelt so hohe Geschwindigkeit bedeutet somit einen vierfach so großen Strömungswiderstand.
Darüber hinaus hat die Größe der senkrecht angeströmten Fläche A des Körpers einen entscheidenden Einfluss auf den Strömungswiderstand. Dabei handelt es sich um die in Strömungsrichtung projizierte Fläche. Man kann sich dabei vorstellen, als würde man den Gegenstand in Strömungsrichtung mit einer Lampe beleuchten. Der entstehende Schattenwurf auf einer hinter dem Gegenstand befindlichen Wand entspräche dann der projizierten Fläche.

Die projizierte Fläche beschreibt lediglich die Größe der angeströmten Körperoberfläche, nicht aber dessen genaue Form. Die Form ist aber von entscheidender Bedeutung, wenn es um den Strömungswiderstand geht. Der Strömungswiderstand einer hohlen Halbkugel ist bei Anströmung gegen die konkave Seite bspw. fast vier Mal so groß wie wenn die konvexe Seite der Halbkugel angeströmt werden würde, obwohl die projizierte Fläche in beiden Fällen offensichtlich dieselbe ist. Diesen Einfluss der Körperform auf den Strömungswiderstand wird über den dimensionslosen Widerstandsbeiwert cw erfasst (auch cw-Wert genannt).
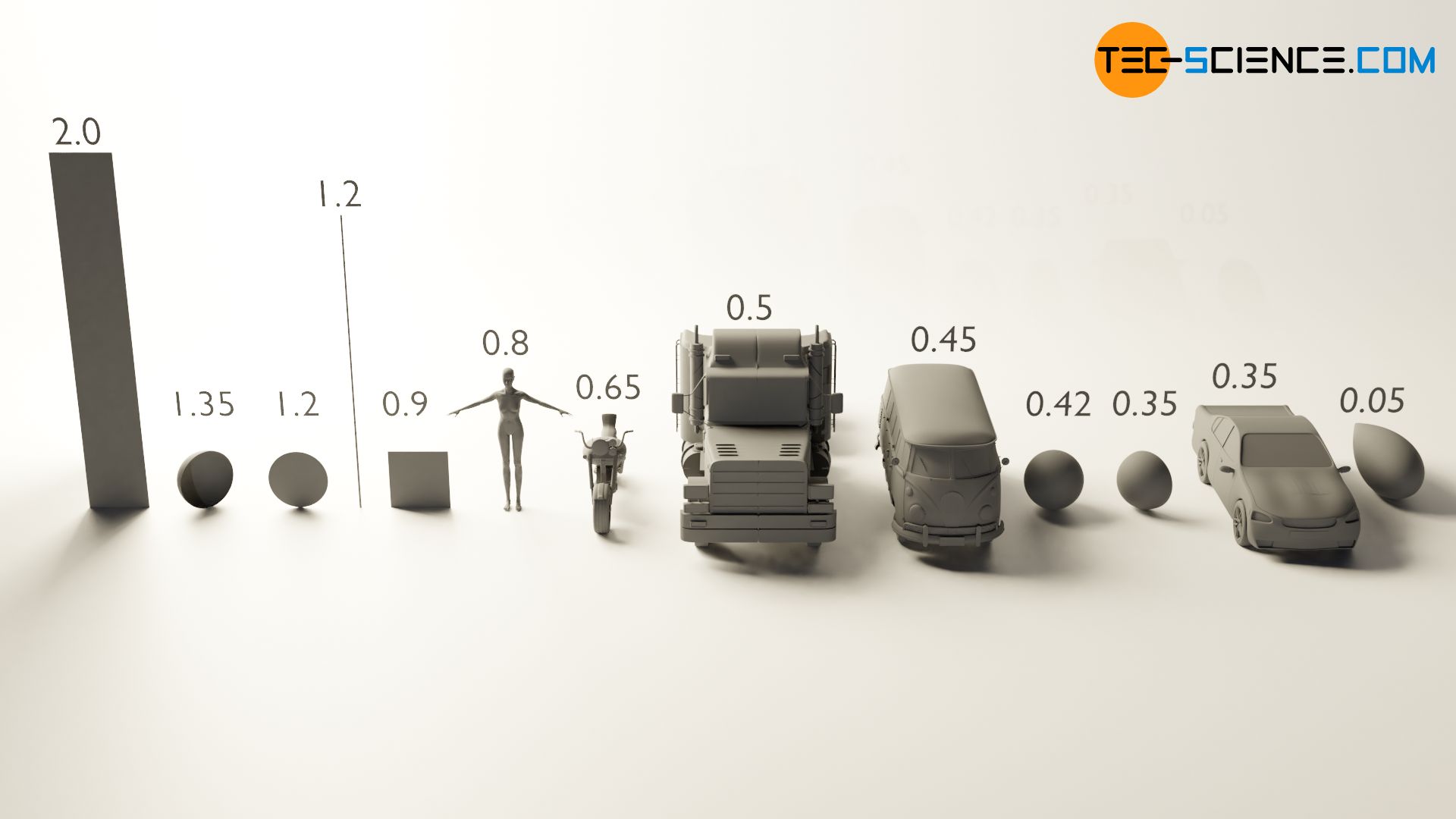
Widerstandsbeiwert von kugelförmigen Körpern in laminaren Strömungen
Die Widerstandsbeiwerte von geometrisch komplexen Gegenständen werden in der Regel durch Experimente in Windkanälen oder Wasserkanälen bestimmt. Für relativ einfache geometrische Formen wie glatte Kugeln hat man unter vereinfachten Bedingungen jedoch versucht die Widerstandsbeiwerte auch rechnerisch zu ermitteln. Der Wissenschaftler Kaskas stellte dabei folgende Näherungsformel zur Berechnung des Widerstandsbeiwerts von sphärischen Körpern in laminaren Strömungen auf:
\begin{align}
&\boxed{c_\text{w} = \frac{24}{Re} +\frac{4}{\sqrt{Re}}+0,4}~~Re<2\cdot 10^5 \\[5px]
\end{align}
In dieser Gleichung bezeichnet Re die dimensionslose Strömungsgeschwindigkeit in Form der Reynoldszahl. Für kugelförmige Körper bestimmt sich die Reynoldszahl über die Umströmgeschwindigkeit v∞, die Dichte ϱ des Fluids und dessen dynamischer Viskosität η sowie dem Durchmesser d der Kugel als charakteristische Länge:
\begin{align}
&\boxed{Re = \frac{v_\infty~d~\rho}{\eta}} \\[5px]
\end{align}
Gesetz von Stokes für kleine Reynoldszahlen
Hinter den Kugeln bilden sich trotz laminarer Strömung in der Regel Strömungsablösungen und Verwirbelungen, die bei hohen Reynoldszahlen einen turbulenten Nachlauf zur Folge haben. Die untere Abbildung zeigt hierzu schematisch das Stromlinienbild einer laminar umströmten Kugel mit turbulentem Nachlauf.

Lediglich bei geringen Umströmgeschwindigkeiten, bei denen die Reynoldszahl kleiner 1 ist, kann näherungsweise von einem symmetrischen Stromlinienbild ausgegangen werden. Eine solche Strömung wird auch als schleichende Strömung bezeichnet und liegt vollständig an der Kugel an und bildet keine Wirbel auf der Abströmseite. Der Wissenschaftler Stokes konnte für diesen Fall aus den Navier-Stokes-Gleichungen folgende Formel zur Bestimmung des Widerstandbeiwertes herleiten:
\begin{align}
&\boxed{c_\text{w} = \frac{24}{Re} }~~Re<1 \\[5px]
\end{align}

Die Formel von Kaskas steht prinzipiell nicht im Widerspruch zur Formel von Stokes. Für kleine Reynolds-Zahlen werden nämlich die beiden letzten Terme in der Näherungsformel von Kaskas gegenüber dem ersten Term vernachlässigbar. Somit nähert sich der Wert aus der Näherungsformel von Kaskas immer mehr dem Widerstandsbeiwert nach Stokes an. Setzt man an dieser Stelle den cw-Wert nach Stokes in die Formel (\ref{f}) ein, dann folgt für den Strömungswiderstand einer vollständig laminar umströmten Kugel folgender Zusammenhang:
\begin{align}
\require{cancel}
&F_\text{w} =\frac{1}{2}~\rho~v_\infty^2~\color{red}{A}~ \color{blue}{c_\text{w}} \\[5px]
&F_\text{w} =\frac{1}{2}~\rho~v_\infty^2~\color{red}{\frac{\pi}{4}d^2}~ \color{blue}{\frac{24}{Re}} \\[5px]
&F_\text{w} =\frac{1}{2}~\bcancel{\rho}~v_\infty^\bcancel{2}~\frac{\pi}{4}d^\bcancel{2}~ \frac{24~\eta}{\bcancel{v_\infty}~\bcancel{d}~\bcancel{\rho}} \\[5px]
&F_\text{w} =\frac{1}{2}~v_\infty~\frac{\pi}{4}d~ 24~\eta \\[5px]
&F_\text{w} =3\pi~\eta~v_\infty~d \\[5px]
&\boxed{F_\text{w} =6\pi~\eta~v_\infty~r} ~~~\text{Gesetz von Stokes}\\[5px]
\end{align}
Der Strömungswiderstand einer laminar umströmten Kugel hängt also lediglich von der Viskosität des Fluids η, der Strömungsgeschwindigkeit v∞ und dem Radius r der Kugel ab. Beachte, dass die Strömungsgeschwindigkeit dabei keinen quadratischen Einfluss mehr auf den Strömungswiderstand hat, sondern einen linearen!
Das Stokes’sche Reibungsgesetz für laminar umströmte Kugeln besagt, dass der Strömungswiderstand proportional zur Viskosität des Mediums, zur Strömungsgeschwindigkeit und zum Radius der Kugel ist!
Den relativ einfachen Zusammenhang zwischen der Viskosität eines Fluids und der Widerstandskraft nutzt man bspw. bei sogenannten Kugelfall-Viskosimetern gezielt aus, um anhand der Sinkgeschwindigkeit einer Kugel auf die Viskosität eines Fluids zu schließen.







