Zur Beschreibung des Wärme- und Stofftransports führt man dimensionslose Kennzahlen ein, um die Transportvorgänge innerhalb der Grenzschichten zu beschreiben.
Zwischen einem strömenden Fluid und einer festen Oberfläche, kommt es zur Ausbildung verschiedener Grenzschichten, auf die in den verlinkten Artikeln ausführlich eingegangen wurde:
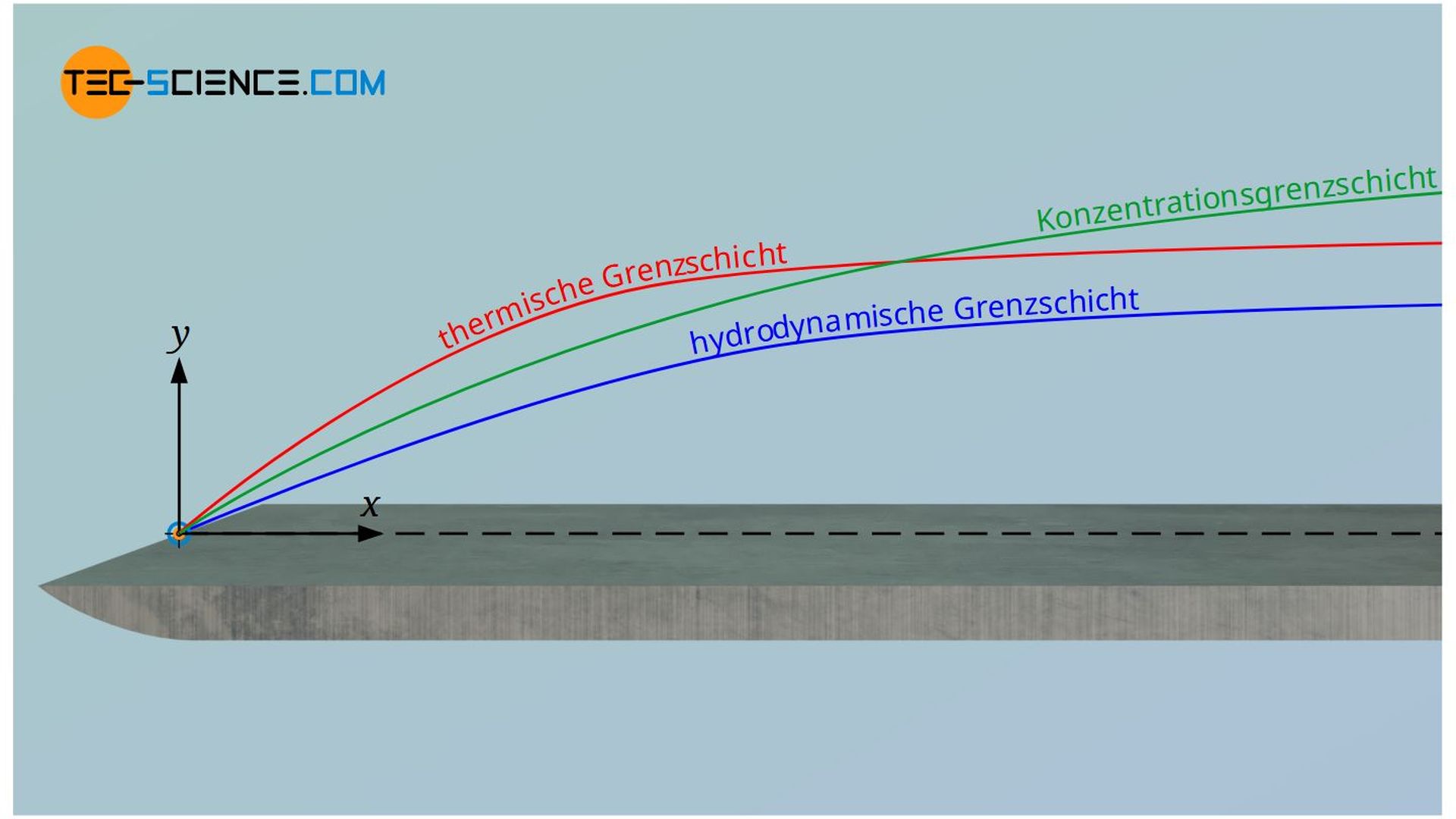
- Geschwindigkeitsgrenzschicht (hydrodynamische Grenzschicht)
- Temperaturgrenzschicht (thermische Grenzschicht)
- Konzentrationsgrenzschicht (Stoffgrenzschicht)
Beachte, dass sich die drei Grenzschichten im Allgemeinen voneinander unterscheiden und nicht im selben Maße verlaufen. Während sich bspw. eine Geschwindigkeitsgrenzschicht bei Strömungsvorgängen immer entwickeln wird, muss eine Temperaturgrenzschicht oder eine Konzentrationsgrenzschicht nicht immer vorhanden sein. Hat zum Beispiel die Wand und das Fluid dieselbe Temperatur, dann existiert kein Temperaturgradient und somit auch keine thermische Grenzschicht. Analog gilt dies für das Strömen von homogenen Fluiden, die keinen Konzentrationsgradienten und somit auch keine Konzentrationsgrenzschicht aufweisen.
In alle Grenzschichten wirken charakteristische Gradienten, die zu entsprechenden Impuls-, Wärme- und Stoffströmen führen. Die untere Tabelle stellt die jeweiligen Transportgleichungen nochmals gegenüber. Auf diese Tabelle wurde im Artikel Thermische Grenzschicht und Konzentrationsgrenzschicht bereits näher eingegangen. Sie soll an dieser Stelle nur nochmals die Analogien der jeweiligen Transportvorgänge zeigen.
| Impulstransport | Wärmetransport | Stofftransport | |
|---|---|---|---|
| Gesetz von | Newton | Fourier | Fick |
| \begin{align} \notag &\boxed{\tau = \eta~ \frac{\partial v}{\partial y}} \left(= \dot p_A\right) \end{align} | \begin{align} \notag &\boxed{\dot q = – \lambda ~\frac{\partial T}{\partial y}} \end{align} | \begin{align} \notag &\boxed{\dot n = – D~ \frac{\partial c}{\partial y}} \end{align} | |
| Antrieb | Geschwindigkeits- gradient | Temperatur- gradient | Konzentrations- gradient |
| Charakteristische Größe | dynamische Viskosität \(\eta\) | Wärmeleit- koeffizient \(\lambda\) | Diffusions- koeffizient \(D\) |
| kinematische Viskosität \begin{align} \notag &{\nu = \frac{\eta}{\rho}} \\[5px] \end{align} | Temperatur- leitfähigkeit \begin{align} \notag &{a = \frac{\lambda}{\rho \cdot c_p}} \\[5px] \end{align} | ||
| Stromdichte | Impulsstromdichte | Wärmestromdichte | Stoffstromdichte |
Beachte, dass die kinematische Viskosität ν über die Stoffdichte in direktem Zusammenhang zur dynamischen Viskosität steht. Sie ist also ebenso eine charakteristische Größe des Impulstransports. Auf die ähnliche Weise steht die Temperaturleitfähigkeit a über die Dichte und der spezifischen Wärmekapazität cp in direktem Zusammenhang zur Wärmeleitfähigkeit und kann als charakteristische Größe für den Wärmetransport betrachtet werden.
Die drei Grenzschichten existieren nicht unabhängig voneinander, sondern beeinflussen sich gegenseitig. So bedeutet bspw. eine geringe Strömungsgeschwindigkeit einen relativ geringen Abtransport von Wärme. Dies führt zu einer verstärkten Erwärmung des Fluids. Hierdurch ändert sich nicht nur der Stofftransport durch Diffusion, sondern auch auch die temperaturabhängige Viskosität. Dies bedeutet ein geändertes Strömungsverhalten, was wiederum den Wärmetransport beeinflusst. Die Vorgänge in den jeweiligen Grenzschichten beeinflussen sich als gegenseitig.
Möchte man den Impuls-, Wärme- und Stofftransport für unterschiedlich große System miteinander vergleichen, dann ist dies folglich nur möglich, wenn die gesamten Grenzschichten bzw. die darin ablaufenden Vorgänge im selben Verhältnis zueinander stehen. Aus diesem Grund führt man insgesamt drei dimensionslose Kennzahlen ein. Diese Kennzahlen setzen jeweils zwei charakteristische Größen der Grenzschichten miteinander ins Verhältnis. Zu diesen dimensionslosen Kenngrößen zählt die Prandtl-Zahl Pr, die Schmidt-Zahl Sc und die Lewis-Zahl Le:
| Prandtl-Zahl Pr | Schmidt-Zahl Sc | Lewis-Zahl Le |
| Verhältnis von Impulstransport zu Energietransport | Verhältnis von Impulstransport zur Stofftransport | Verhältnis von Energietransport zur Stofftransport |
| \begin{align} \notag &\boxed{Pr = \frac{\nu}{a}}=\frac{\eta \cdot c_p}{\lambda} \\[5px] \end{align} | \begin{align} \notag &\boxed{Sc = \frac{\nu}{D}} =\frac{\eta}{\rho \cdot D}\\[5px] \end{align} | \begin{align} \notag &\boxed{Le = \frac{a}{D}}=\frac{\lambda}{\rho \cdot c_p \cdot D} \\[5px] \end{align} |
Bei genauerer Betrachtung zeigt sich, dass das Verhältnis von Schmidt-Zahl und Prandtl-Zahl, gerade der Lewis-Zahl entspricht:
\begin{align}
\require{cancel}
& \frac{Sc}{Pr}= \frac{\frac{\nu}{D}}{\frac{\nu}{a}}=\frac{\bcancel{\nu} \cdot a}{D \cdot \bcancel{\nu}} = \frac{a}{D }=Le \\[5px]
&\boxed{Le=\frac{Sc}{Pr}}
\end{align}
Die drei Grenzschichten sind also durch jeweils zwei dimensionslose Kennzahlen vollständig charakterisiert, da sich die dritte Kenngröße hieraus dann ermitteln lässt. Diese dimensionslosen Kennzahlen haben große praktische Bedeutung für die Übertragbarkeit von Modellversuchen auf die spätere Realität. Denn nur wenn diese dimensionslosen Kennzahlen für das Modell dieselben sind wie für den realen Anwendungsfall, kann man von physikalisch ähnlichen Vorgängen von Impuls-, Energie- und Stofftransport ausgehen.
Beachte, dass die Definitionen der Kenngrößen nicht etwa willkürlich erfolgt, sondern durch die Ähnlichkeitstheorie begründet ist. Die dimensionslosen Kennzahlen werden deshalb auch als Ähnlichkeitskenngrößen bezeichnet. Diese Kenngrößen bieten somit die Möglichkeit, Strömungsprozesse unabhängig der Größe des Systems ganz allgemein zu beschreiben. Sie sind wichtige Bindeglieder zwischen Modellmaßstab und realem Maßstab. Zu solchen Ähnlichkeitskenngrößen zählt bspw. auch die Reynolds-Zahl, die der Charakterisierung des kinematischen Strömungsverhaltens dient.
Auf die oben genannten Kenngrößen wird in den folgenden Artikeln näher eingegangen:






