Hydrodynamische Grenzschicht

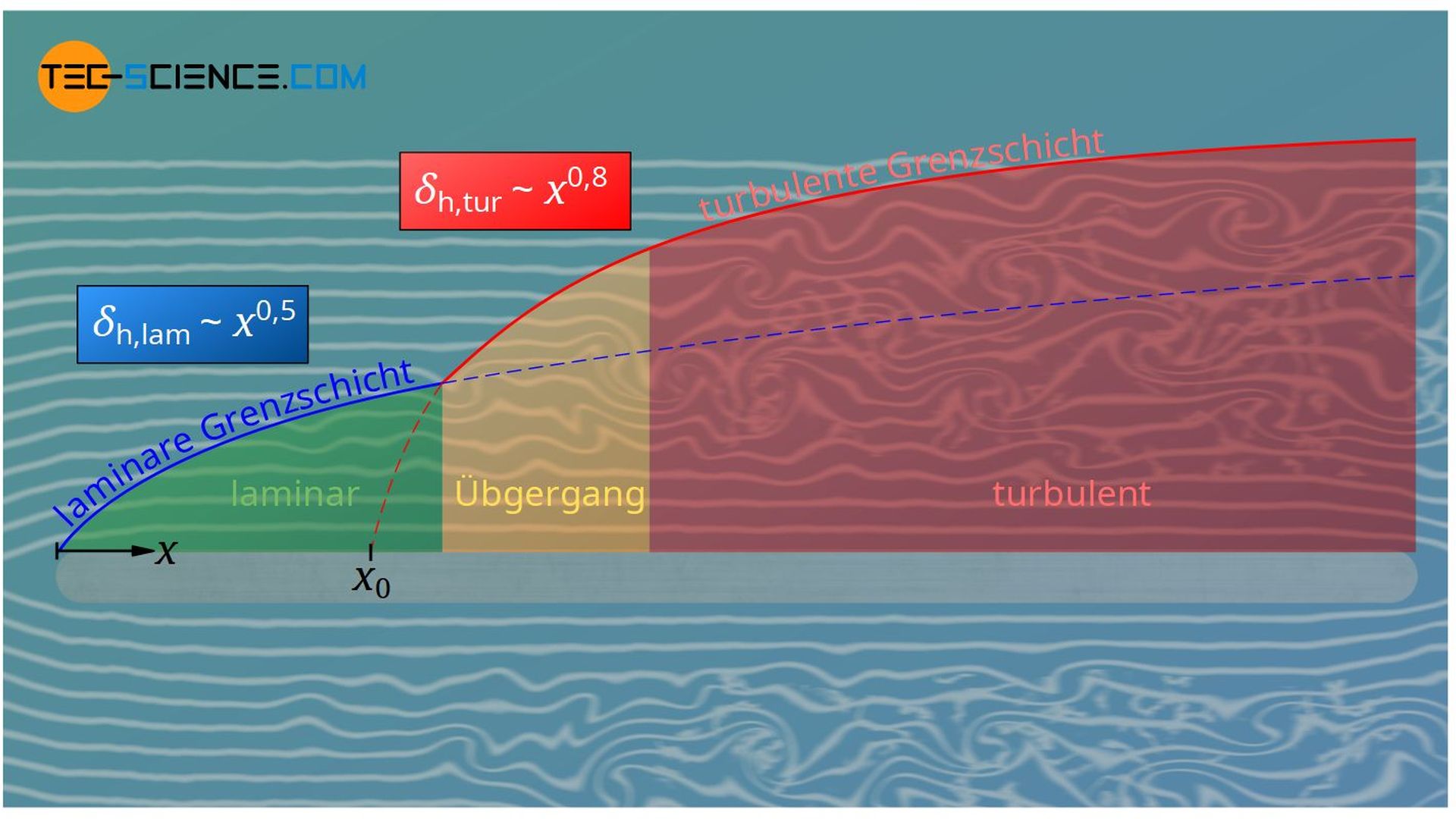
Die hydrodynamische Grenzschicht einer Strömung beeinflusst den Wärme- und Stofftransport entscheidend.

Einleitung

In diesem Artikel betrachten wir die Grenzschichten zwischen einem Festkörper und einem strömenden Fluid etwas näher. Solche Grenzschichten beeinflussen zum Beispiel im entscheidenden Maße den konvektiven Wärmeübergang. Als Beispiel betrachten wir hierzu eine isotherm beheizte Platte mit der Temperatur T₀. Diese Platte wird längs von einem Fluid angeströmt. Die konstante Anströmgeschwindigkeit vor der Platte sei mit v_∞ bezeichnet. Die Temperatur der ungestörten Anströmung betrage T_∞.

Intermolekulare Kräfte innerhalb des Fluids und Reibungskräfte zwischen Fluid und fester Oberfläche beeinflussen die Strömungsgeschwindigkeit. Es kommt zur Ausbildung eines typischen Geschwindigkeitsprofils. Die Fluidteilchen haften aufgrund der Reibungskräfte unmittelbar an der Wand, d.h. die Geschwindigkeit der Strömung ist dort null (Haftbedingung genannt). Mit zunehmendem Abstand zur Wand nimmt die Geschwindigkeit zu. In einem gewissen Abstand erreicht die Strömungsgeschwindigkeit schließlich die Geschwindigkeit v_∞ der ungestörten Strömung an.

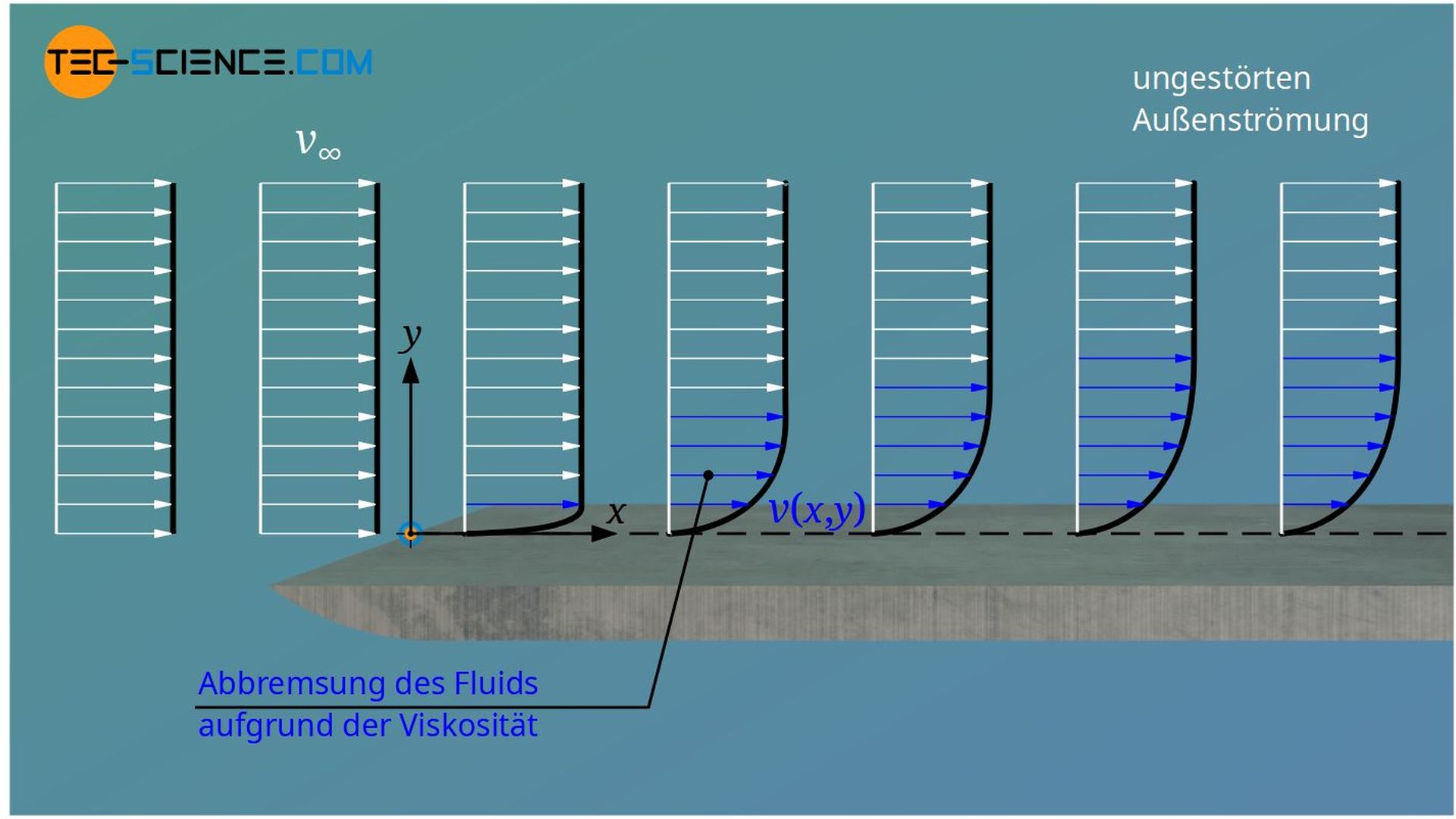
Einfluss der Viskosität auf die Störung der Strömung

Wie stark jener Bereich ausgeprägt ist, bis wohin die Strömung in einem bestimmten Abstand zur Wand wieder die ungestörte Geschwindigkeit der freien Strömung erreicht (weiße Pfeile in der oberen Abbildung), hängt maßgeblich von der Viskosität des Fluids ab. Bei Fluiden mit geringen Viskositäten wie bspw. Wasser oder Gase, sind die intermolekularen Anziehungskräfte relativ gering. Stellt man sich das strömende Fluid aus vielen kleinen Schichten aufgebaut vor, dann ist die Anziehungskraft zwischen diesen Schichten relativ gering. Sie behindern sich also nicht so sehr gegenseitig in ihrer Bewegung, wenn diese mit unterschiedlichen Geschwindigkeiten strömen. Fluide mit niedrigen Viskositäten erreichen deshalb bereits in einem relativ geringen Abstand zur Wand wieder die ungestörte Geschwindigkeit der freien Strömung.

Bei Fluiden mit höheren Viskositäten wie bspw. Öle (oder besonders anschaulich bei Honig), sind die intermolekularen Kohäsionskräfte hingegen relativ hoch. Die einzelnen Fluidschichten üben deshalb relativ starke Anziehungskräfte aufeinander aus und beeinflussen sich stark in ihrer gegenseitigen Bewegung. Dieser Bereich innerhalb dessen die Strömung gestört ist, ist bei hochviskosen Fluiden deshalb größer. Dieser gestörte Geschwindigkeitsbereich, der unter Beeinflussung von Schubspannungen zwischen den Fluidschichten steht, wird auch als Geschwindigkeitsgrenzschicht oder hydrodynamische Grenzschicht bezeichnet.

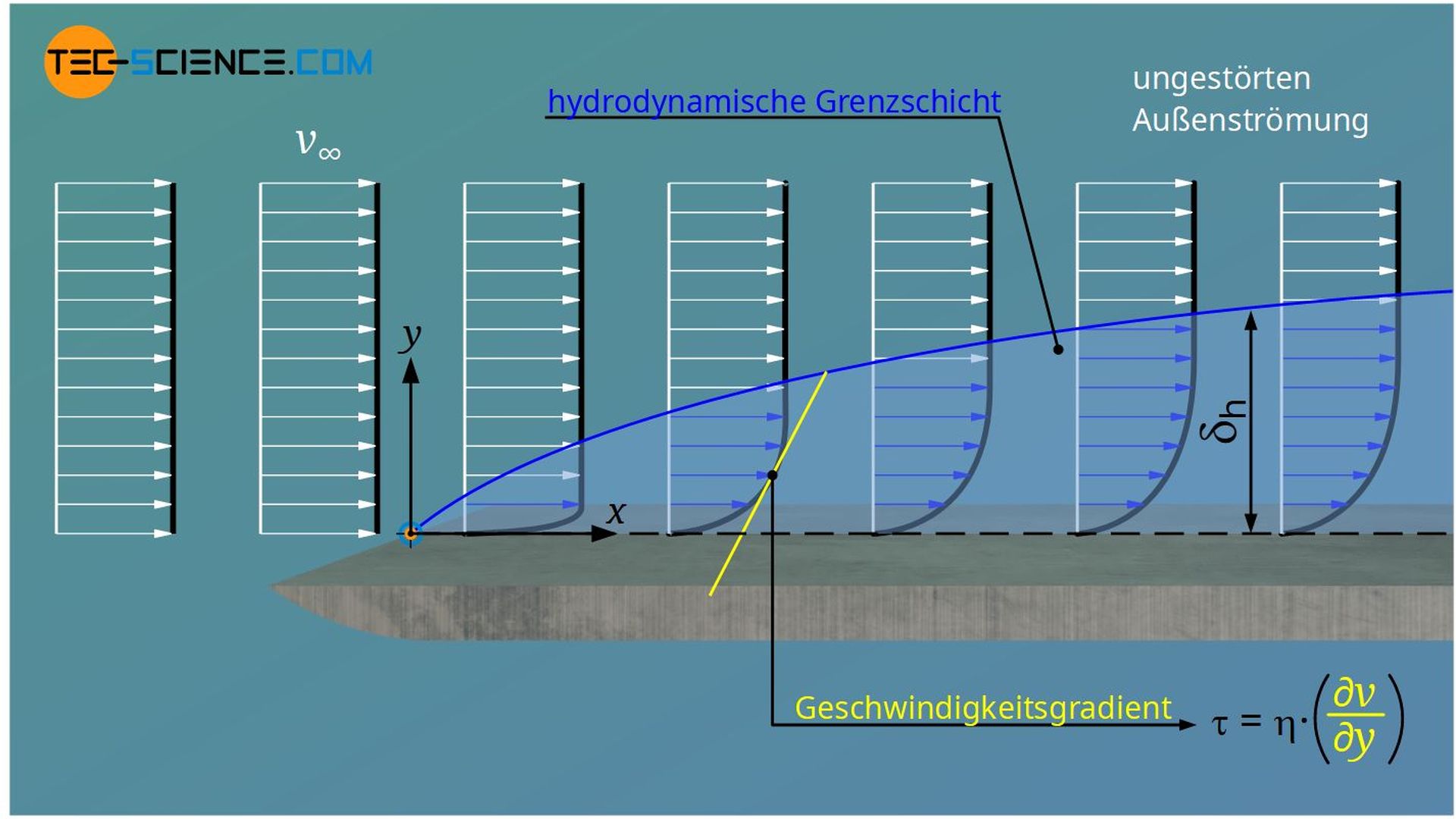
Jener Randbereich bis wohin die lokale Strömungsgeschwindigkeit 99 % der ungestörten Strömung erreicht hat, wird auch als Geschwindigkeitsgrenzschicht oder hydrodynamische Grenzschicht bezeichnet.

Geschwindigkeitsgradienten und Schubspannungen

Die Geschwindigkeitsgrenzschicht ist also dadurch definiert, dass innerhalb deren Geschwindigkeitsgradienten und somit auch Schubspannungen τ existieren. Beachte, dass gemäß des Newtonsches Reibungsgesetz das Vorhandensein von Geschwindigkeitsgradienten immer auch die Existenz von Schubspannungen bedeuten:

„Schubspannung = Viskosität x Geschwindigkeitsgradient“

Diese Schubspannungen sind letztlich dafür verantwortlich, dass die Fluidschichten abgebremst werden und sich anschließend ein Gleichgewicht zwischen dem äußeren Druckgradienten (als Antrieb für die Strömung) und den Schubspannungen bildet.

Da also außerhalb der hydrodynamischen Grenzschicht keine Geschwindigkeitsgradienten existieren, sind auch die Schubspannungen vernachlässigbar klein. In dieser ungestörten Strömung spielt die Viskosität des Fluids also keine Rolle. Innerhalb der Grenzschicht sind die Schubspannungen in der Regeln nicht mehr vernachlässigbar und beeinflussen die Strömung entscheidend. Auch wenn die Grenzschicht sehr präzise definiert ist, so gehen die Eigenschaften der Strömung innerhalb und außerhalb dieser „scharfen“ Grenze fließend ineinander über!

Verlauf der laminaren Grenzschicht

Die Dicke der Grenzschicht nimmt mit zunehmendem Abstand von der Plattenkante zunächst zu, da immer mehr Fluidschichten unter den Einfluss der Reibung gelangen. Jede Fluidschicht bremst sozusagen die darüber befindliche allmählich ab. Dies bezeichnet man auch als Anlaufströmung. Ab einem hinreichend großen Abstand ändert sich die Dicke der Grenzschicht δ_h dann allerdings (fast) nicht mehr. Es hat sich das besagte Gleichgewicht zwischen Druckgradient und Reibungskraft eingestellt. Man spricht in diesem Fall dann auch von einer vollständig ausgebildeten Grenzschicht.

Für eine Strömung über eine dünne ebene Platte können die Grenzschichtgleichungen analytisch gelöst werden (Blasius-Lösung). Voraussetzung is ferner, dass die Strömung laminar und inkompressibel ist und kein Druckgradient infolge von Reibungskräften entlang der Platte existieren. Die Dicke der Grenzschicht δ_h in einem Abstand x von der Plattenkante ist dann abhängig von der lokalen Reynoldszahl Re_x und kann wie folgt ermittelt werden:

\begin{align}
&\boxed{\delta_\text{h,lam}= \frac{5 \cdot x}{\sqrt{Re_x}}} ~~~Re_x = \frac{v_\infty \cdot x}{\nu} \\[5px]
&\boxed{\delta_\text{h,lam} \sim x^{0,5}} \\[5px]
\end{align}

Darin bezeichnet v_∞ die Geschwindigkeit der ungestörten Außenströmung und ν (griechischer Kleinbuchstaben Nu) die kinematische Viskosität des Fluids. Im Falle von Wasser oder Luft und einer Plattendimension in der Größenordnung von 1 m und Geschwindigkeiten im Bereich von einigen Metern pro Sekunde, liegen die Grenzschichtdicken also in der Größenordnung von 1 mm.

Impulstransport

Schubspannung beeinflussen die Geschwindigkeit der Strömung (Impuls der Strömung), sodass man im Zusammenhang mit der Viskosität deshalb auch von einem Impulstransport oder einer Impulsdiffusion spricht. Dieser Transport bzw. diese Diffusion des Impulses findet zwischen den einzelnen Fluidschichten statt, sodass es zu einer entsprechenden Änderung der Strömungsgeschwindigkeit in den einzelnen Fluidschichten kommt (siehe hierzu auch den Artikel Thermische Grenzschicht und Konzentrationsgrenzschicht, in dem eine Analogie zu den anderen Transportvorgängen gezeigt wird).

Und tatsächlich ist vor allem bei Gasen die Viskosität hauptsächlich auf ein solches Diffundieren von Fluidteilchen in die umgebenden Fluidschichten zurückzuführen. Aufgrund der ungeordneten Wärmebewegung diffundieren bspw. Fluidteilchen aus langsamen Fluidschichten, in sich schneller bewegende Fluidschichten ein. Die langsamen Fluidteilchen führen somit zu einer Art Abbremsung der schnelleren Fluidschichten. Die Wirkung ist letztlich dieselbe, wie wenn Reibungskräfte in Form von Kohäsionskräfte zwischen den Schichten wirken. Solche intermolekularen Anziehungskräfte sind bei Gasen allerdings nur sehr schwach ausgeprägt, sodass die Diffusion von Fluidteilchen Hauptursache für die Viskosität von Gasen ist. Der Begriff Impuls-Diffusion ist tatsächlich wörtlich zu nehmen.

Laminare und turbulente Grenzschicht

Grenzschichten können nicht nur laminar oder turbulent sein, sondern auch aus einer Mischung von beiden Strömungsarten bestehen. Tatsächlich kommt dies bei umströmten Körpern meist vor, da weder der Körper optimal stromlinienförmig gestaltet ist, noch die Oberfläche perfekt glatt ist. Zudem ist eine Strömung niemals perfekt laminar, sondern beinhaltet immer einen gewissen Turbulenzgrad (d.h. kleine Geschwindigkeitsschwankungen quer zur Hauptströmungsrichtung). Bereits die Brownsche Wärmebewegung der Teilchen bringt einen gewissen Turbulenzgrad mit sich, die dient somit als Störung.

Betrachten wir nun wieder unsere Platte. Entweder sind also bereits kleine Störungen in der Strömung vorhanden oder diese bilden sich beim Aufströmen auf die Platte. Beeinflusst durch die Grenzschicht selbst, schaukeln sich die Störungen zunehmend auf. Bis zu einem gewissen Grad können diese Störungen aber zunächst vom Fluid ausgeglichen werden. Dieses Ausgleichen gelingt umso besser, je höher die Viskosität des Fluids ist (starker innerer Zusammenhalt) und je geringer die Strömungsgeschwindigkeit ist (geringere Trägheitskräfte).

Ab einem kritischen Punkt x_krit haben sich die Störungen allerdings derart verstärkt, dass sie instabil werden. Die Zähigkeit des Fluids reicht dann nicht mehr aus, um den Trägheitskräften etwas entgegen zu setzen. Die laminare Strömung schlägt nach einem relativ kurzen Übergangsgebiet in eine turbulente Strömung um. Dieser Umschlag findet bei kritischen Reynoldszahlen von etwa 5⋅10⁵ statt. Der kritische Punkt wird auch als Umschlagpunkt bezeichnet.

\begin{align}
&\boxed{Re_\text{krit}= \frac{v_\infty \cdot x_\text{krit}}{\nu}=5 \cdot 10^5}
\end{align}

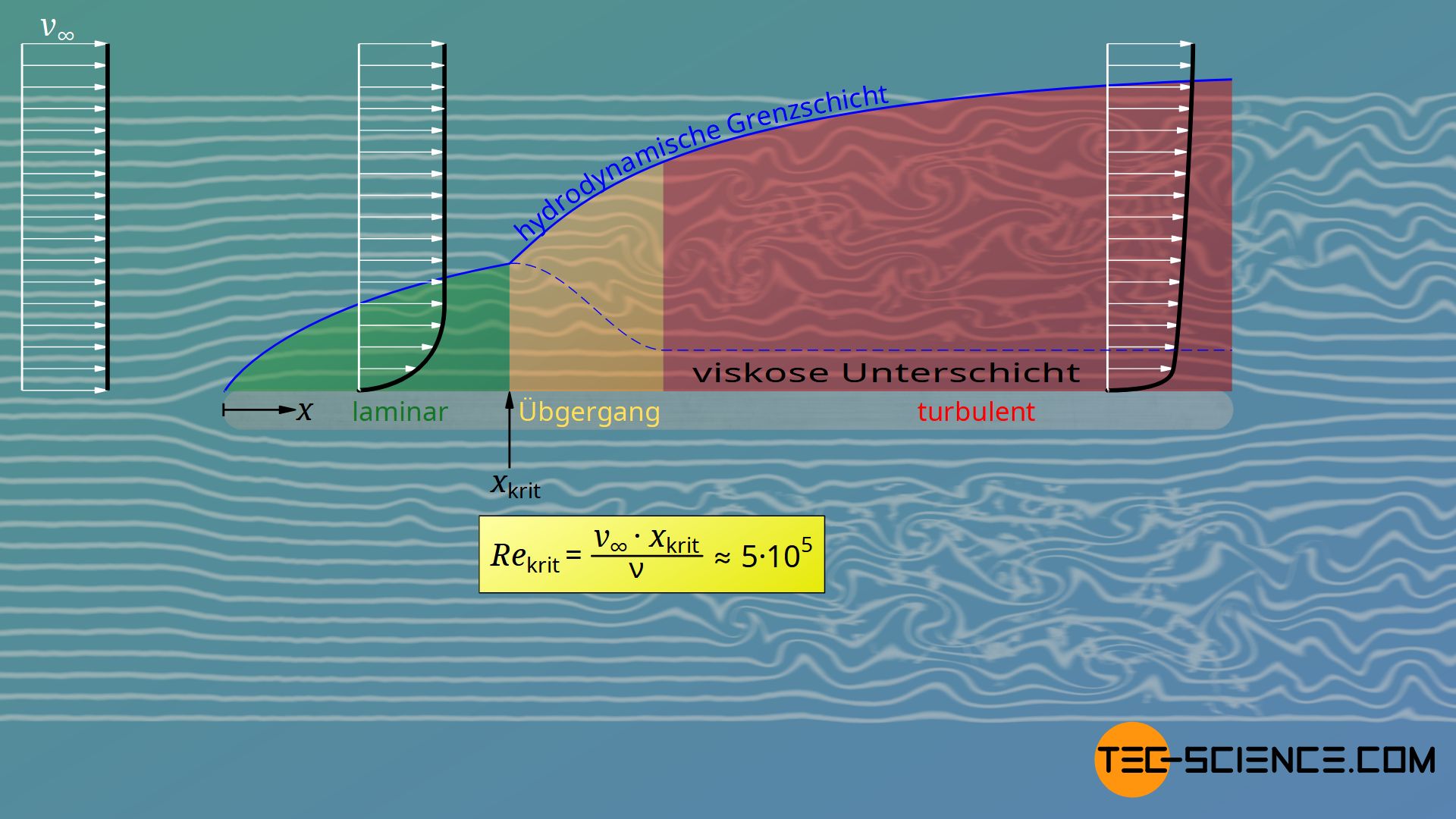
Die Dicke der Grenzschicht wächst im turbulenten Bereich aufgrund der Verwirbelungen stärker an als im laminaren Bereich. Sich bildende Wirbel bedeuten aber auch, dass die Fluidteilchen nicht nur längs der Platte entlang strömen, sondern auch quer dazu. Diese Querströmungen führen zu einem verstärkten Impulsaustausch, vor allem in der Nähe der Wand. Dies ist auch der Grund, weshalb die (zeitlich gemittelte) Strömungsgeschwindigkeit nahe der Platte im turbulenten Bereich schneller ansteigt als im laminaren Bereich. Das turbulente Geschwindigkeitsprofil ist „bauchiger“ als das laminare. Der größere Geschwindigkeitsgradient an der Wand ist auch der Grund, weshalb turbulente Strömungen zu einem höheren Reibungswiderstand führen.

Viskose Unterschicht

Querströmungen in turbulenten Strömungen können sich grundsätzlich nur dort ausbilden, wo die Fluidteilchen auch den Raum haben, quer zu strömen. Unmittelbar an der Wand ist dies allerdings nicht möglich, da die Wand den Fluidteilchen sozusagen keinen Raum gibt. Deshalb bildet sich in unmittelbarer Nähe der Wand eine laminare Strömung aus. Man bezeichnet dies auch als laminare Unterschicht bzw. viskose Unterschicht. Die Dicke dieser Unterschicht beträgt nur ein Bruchteil der Dicke der gesamten turbulenten Grenzschicht (in der Abbildung oben zur Veranschaulichung übertrieben dargestellt).

Überdeckt die viskose Unterschicht die eigentlichen Rauigkeiten der Plattenoberfläche, dann beeinflussen die Oberflächenrauigkeiten nicht die die darüber befindliche turbulente Schicht. In diesem Fall ist bspw. der Reibungswiderstand zwischen Fluid und Wand nicht durch die Oberflächenrauhigkeit bestimmt. Man spricht dann auch von einer hydraulisch glatten Oberfläche.

Die laminare Unterschicht ist auch der Grund weshalb selbst bei turbulenten Strömungen das Newtonsche Reibungsgesetz direkt an der Wand weiterhin gültig ist. Damit können die höheren Wandschubspannungen aufgrund des größeren Geschwindigkeitsgradienten direkt mit Hilfe des Newtonschen Reibungsgesetzes erklärt werden.

Verlauf der turbulenten Grenzschicht

Im Artikel zum Hagen-Poiseuille Gesetz wurde das sogenannten 1/7-Potenzgesetz zur Beschreibung der Geschwindigkeitsverteilung v(z) für turbulente Rohrströmungen bereits vorgestellt:

\begin{align}
&\boxed{v(y)=v_\text{max} \cdot \left(\frac{y}{R}\right)^\frac{1}{7}} ~~~~0<y<R\\[5px]
\end{align}

Darin bezeichnet z den Abstand zur Rohrwand und R den Radius des Rohres. Der Rohrradius beschreibt gewissermaßen die Dicke der Grenzschicht. Die maximale Geschwindigkeit v_max tritt in diesem Fall in der Mitte des Rohres auf.

Stellen wir uns nun vor, wir machen den Durchmesser des Rohres in Gedanken immer größer und größer. Schließlich erhält man im Extremfall eine ebene Wand, über die ein Fluid strömt. Die maximale Geschwindigkeit entspricht dann der Geschwindigkeit der ungestörten Strömung v_∞. Anstelle des Radius tritt die Grenzschichtdicke δ_h(x), die offensichtlich eine Funktion von x ist. Für die zeitlich gemittelte Geschwindigkeit v(x,y) innerhalb der turbulenten Grenzschicht gilt damit:

\begin{align}
&\boxed{\overline{v}(x,y)=v_\infty \cdot \left(\frac{y}{\delta_h(x)}\right)^\frac{1}{7}}\\[5px]
\end{align}

Mit Hilfe dieses Ansatzes lässt sich eine Differentialgleichung herleiten, mit der die Grenzschichtdicke δ_h unter Zuhilfenahme empirischer Ansätze ermittelt werden kann. Dabei zeigt sich letztlich, dass die turbulente Grenzschicht wie folgt von der lokalen Reynolds-Zahl abhängt:

\begin{align}
&\boxed{\delta_\text{h,tur}= \frac{0,37 \cdot x}{\sqrt[5]{Re_x}}} ~~~Re_x = \frac{v_\infty \cdot x}{\nu} \\[5px]
&\boxed{\delta_\text{h,tur} \sim x^{0,8}} \\[5px]
\end{align}

Beachte, dass die laminare Grenzschicht mit x^0,5 anwächst und die turbulente Grenzschicht mit x^0,8, d.h. die turbulente Grenzschicht wächst schneller an als die laminare. Die obere Gleichung geht davon aus, dass die Grenzschicht direkt von der Vorderkante an turbulent ist. Im Falle einer Plattenströmung mit laminar-turbulentem Übergang ist der Verlauf der turbulenten Grenzschicht lediglich um einen Betrag x₀ nach hinten verschoben:

\begin{align}
&\boxed{\delta_\text{h,tur}= \frac{0,37 \cdot (x-x_0)}{\sqrt[5]{Re_x}}}
\end{align}