Die Schmidt-Zahl ist eine dimensionslose Ähnlichkeitskenngröße zur Beschreibung des Stoff- und Impulstransports.
Nicht nur der Impulstransport und der Wärmeübergang beeinflussen sich gegenseitig wie im Artikel zur Prandtl-Zahl bereits ausführlich erläutert. Auch Impulstransport und Stoffübergang stehen in wechselseitiger Beziehung. Der Impulstransport ist unter anderem auf die Brownsche Molekularbewegung zurückzuführen. Auf diese Weise diffundieren Fluidpartikel über die Fluidschichten hinweg und müssen sich den neuen Geschwindigkeiten sozusagen anpassen (Impulsaustausch). Ist zusätzlich noch ein Konzentrationsgradient vorhanden, dann diffundieren die Fluidpartikel nicht nur aufgrund der zufälligen Wärmebewegung in andere Fluidschichten, sondern auch aufgrund des Konzentrationsgradienten.
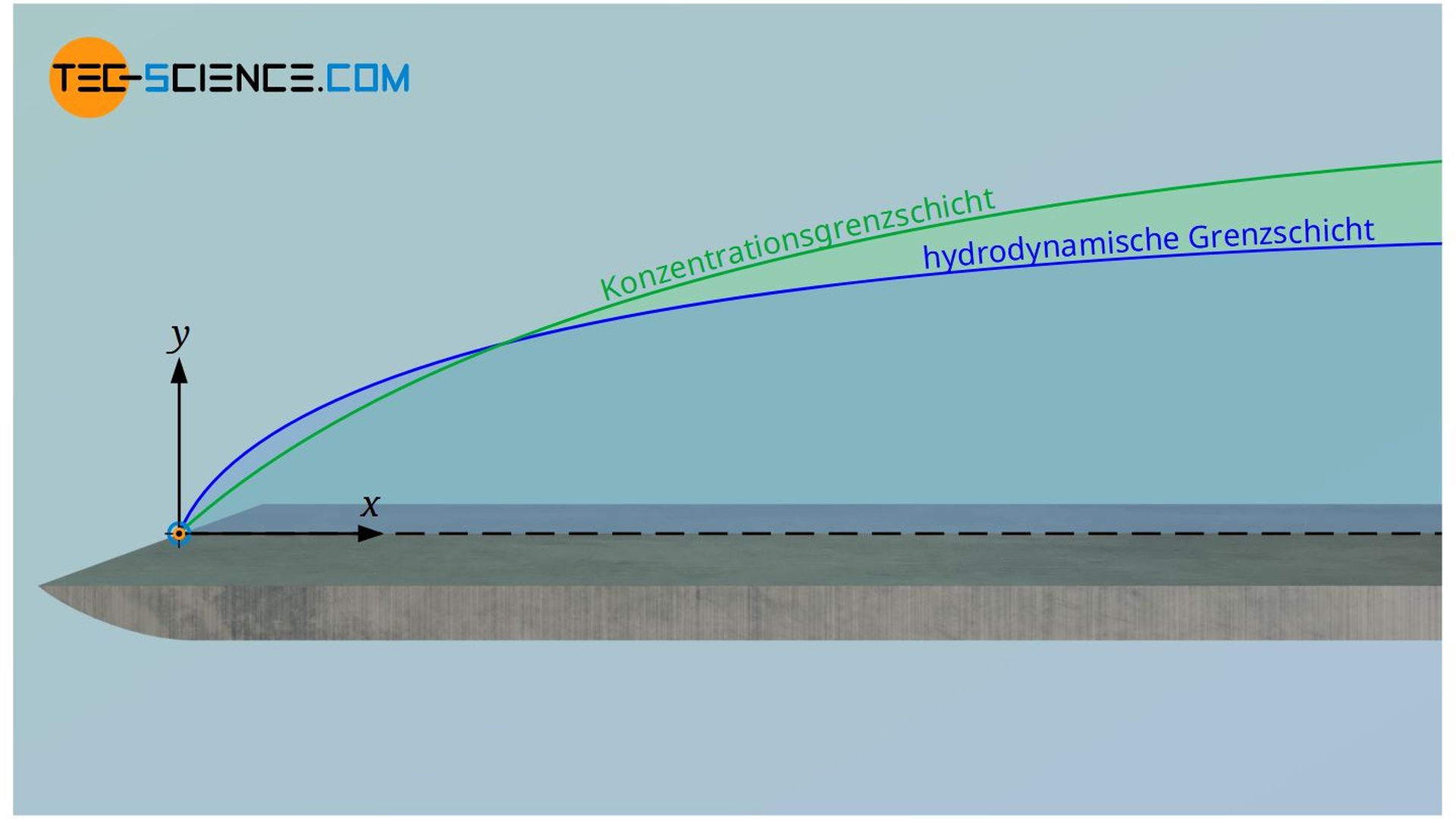
Das Verhältnis von Impulstransport und Stofftransport wird durch die sogenannte Schmidt-Zahl Sc beschrieben. Sie ist sozusagen ein Maß für das Verhältnis der Grenzschichtdicken zwischen hydrodynamischer Grenzschicht und Konzentrationsgrenzschicht. Die Schmidt-Zahl setzt die Viskosität ν eines Fluids ins Verhältnis zu dessen Diffusionskoeffizienten D:
\begin{align}
&\text{Schmidt-Zahl} = \frac{\text{Impulstransport}}{\text{Stofftransport}} \\[5px]
\label{sc}
&\boxed{Sc = \frac{\nu}{D}} ~~~~~\text{Schmidt-Zahl}\\[5px]
\end{align}
Die Schmidt-Zahl kann analog zur Prandtl-Zahl betrachtet werden. Während die Prandtl-Zahl die Diffusion von Wärme beschreibt, charakterisiert die Schmidt-Zahl die Diffusion von Materie. Auf die analoge Weise wie die Prandtl-Zahl zur Bestimmung der Nusselt-Zahl als dimensionslose Wärmeübergangszahl verwendet, wird die Schmidt-Zahl zur Bestimmung der Sherwood-Zahl genutzt, die als dimensionslose Stoffübergangszahl ihr Bedeutung hat. Beide dimensionslosen Übergangszahlen (Nusselt- und Sherwood-Zahl) haben zudem gemeinsam, dass sie ferner durch die Reynolds-Zahl Re beeinflusst werden.
| Wärmetransport | Stofftransport | |
| Kenngröße | Prandtl-Zahl | Schmidt-Zahl |
| Diffusion von … | Wärme | Stoff |
| beeinflusst die … | dimensionslose Wärmeübergangszahl | dimensionslose Stoffübergangszahl |
| Dimensionslose Übergangszahl | Nusselt-Zahl Nu = f(Sc, Re) | Sherwood-Zahl Sh = f(Pr, Re) |
Für die Schmidt-Zahl als dimensionslose Ähnlichkeitskenngröße gilt analog zur Prandtl-Zahl, dass Stoff- und Impulstransporte in zwei unterschiedlich großen Systemen nur dann physikalisch ähnlich sind, wenn die Schmidt-Zahlen identisch sind. Nur dann ist bspw. auch eine Übertragung der gewonnenen Erkenntnisse an einem Modellversuch auf die reale Anwendung möglich.
Die Schmidt-Zahl ist eine dimensionslose Ähnlichkeitskenngröße zur Beschreibung des Stoff- und Impulstransports. Nur bei identischen Schmidt-Zahlen erhält man unabhängig der Größe des gewählten Systems stets physikalisch ähnliche Stoff- und Impulsströme.






