Viskosität von Flüssigkeiten und Gasen

Die Viskosität ist ein Maß für den inneren Fließwiderstand eines Fluids! Sie kommt durch intermolekulare Anziehungskräfte und durch Impulsströme zustande.

Einleitung

Betrachtet man das Fließverhalten von Wasser im Vergleich zu Honig, dann fallen große Unterschiede auf. Gießt man diese Stoffe bspw. auf eine schiefe Ebene, dann fließt Honig deutlich langsamer als Wasser. Honig besitzt sozusagen einen hohen Fließwiderstand, ist also weniger fließfähig. Diese Eigenschaft des Fließwiderstandes nennt man in der Fachsprache Viskosität.

Nicht nur Flüssigkeiten zeigen ein viskoses Verhalten, sondern auch Gase. Bei Gasen ist die Viskosität allerdings weniger stark ausgeprägt. Solche viskose Medien wie Flüssigkeiten und Gase werden auch ganz allgemein als Fluide bezeichnet (lat. fluidus für „fließen“).

Die Viskosität ist ein Maß für den inneren Fließwiderstand eines Fluids!

Herleitung der Viskosität

Wie beschreibt man die Viskosität nun mathematisch? Hierfür ist es zunächst sinnvoll, sich Gedanken zu machen, was die eigentliche Ursache der Viskosität ist. Man kann sich das Fluid hierzu als in viele kleine Schichten aufgebaut vorstellen. Aufgrund der intermolekularen Anziehungskräfte der Fluidteilchen haften diese Schichten aneinander. Diese Anziehungskräfte wirken letztlich wie Reibungskräfte, die unter anderem ursächlich für das viskose Verhalten des Fluids sind. Die Viskosität wird deshalb oft auch als innere Reibung bezeichnet. Aus diesem Grund behindert jede Schicht die jeweils angrenzende Fluidschicht am Strömen. Man kann die Viskosität deshalb etwas präziser formulieren:

Die Viskosität ist ein Maß für die Stärke des Aneinanderhaftens der Fluidschichten!

Man kann die Viskosität somit über die Kraft definieren, die nötig ist, um diese gedachten Fluidschichten gegeneinander zu verschieben. Hierzu denkt man sich das Fluid zwischen zwei horizontalen Platten eingeschlossen. Die untere Platte sei dabei fest und die obere Platte beweglich. Beim Verschieben der oberen Platte, müssen die Fluidschichten gegeneinander abgeschert werden. Dies erfordert je nach Viskosität eine mehr oder weniger starke Kraft. Von welchen Größen diese Kraft beeinflusst wird, soll im Folgenden erläutert werden. Eine solche Strömung zwischen zwei relativ zueinander bewegter Oberflächen wird auch als Couette Strömung bezeichnet.

Einfluss der Geschwindigkeit

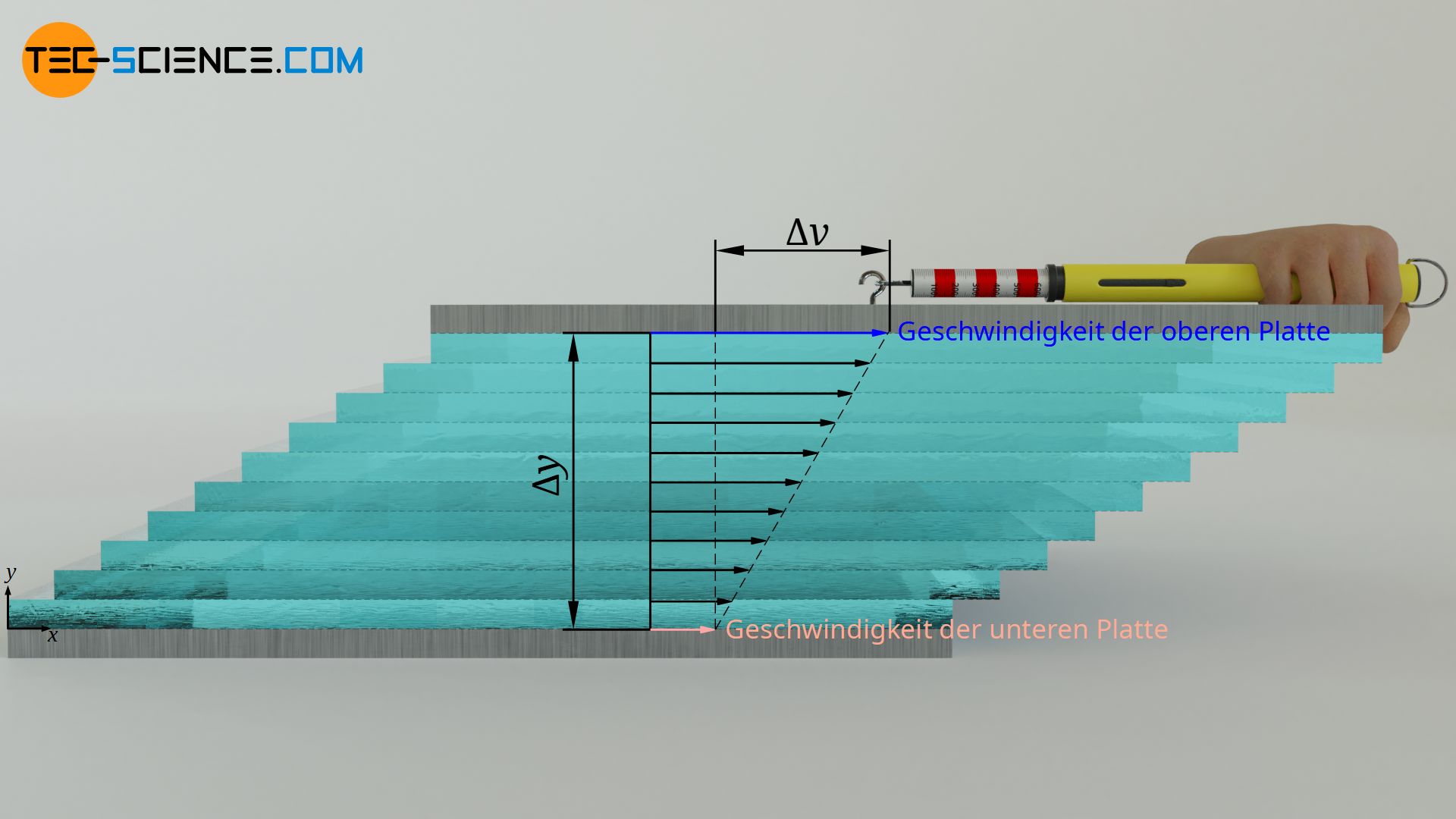
Nicht nur innerhalb des Fluid wirken Kräfte (Kohäsion), sondern auch zwischen Fluid und Wand (Adhäsion). Das Fluid haftet somit regelrecht an den beiden Platten. Man bezeichnet dies auch als sogenannte Haftbedingung. An der unteren Platte beträgt die Geschwindigkeit der Fluidschicht somit null und steigt linear bis auf die Geschwindigkeit der oberen Platte an. Je höher die Geschwindigkeit der oberen Platte ist, desto stärker müssen die Fluidschichten pro Zeiteinheit offensichtlich gegeneinander verschoben werden. Umso höher ist folglich die hierfür benötigte Kraft.

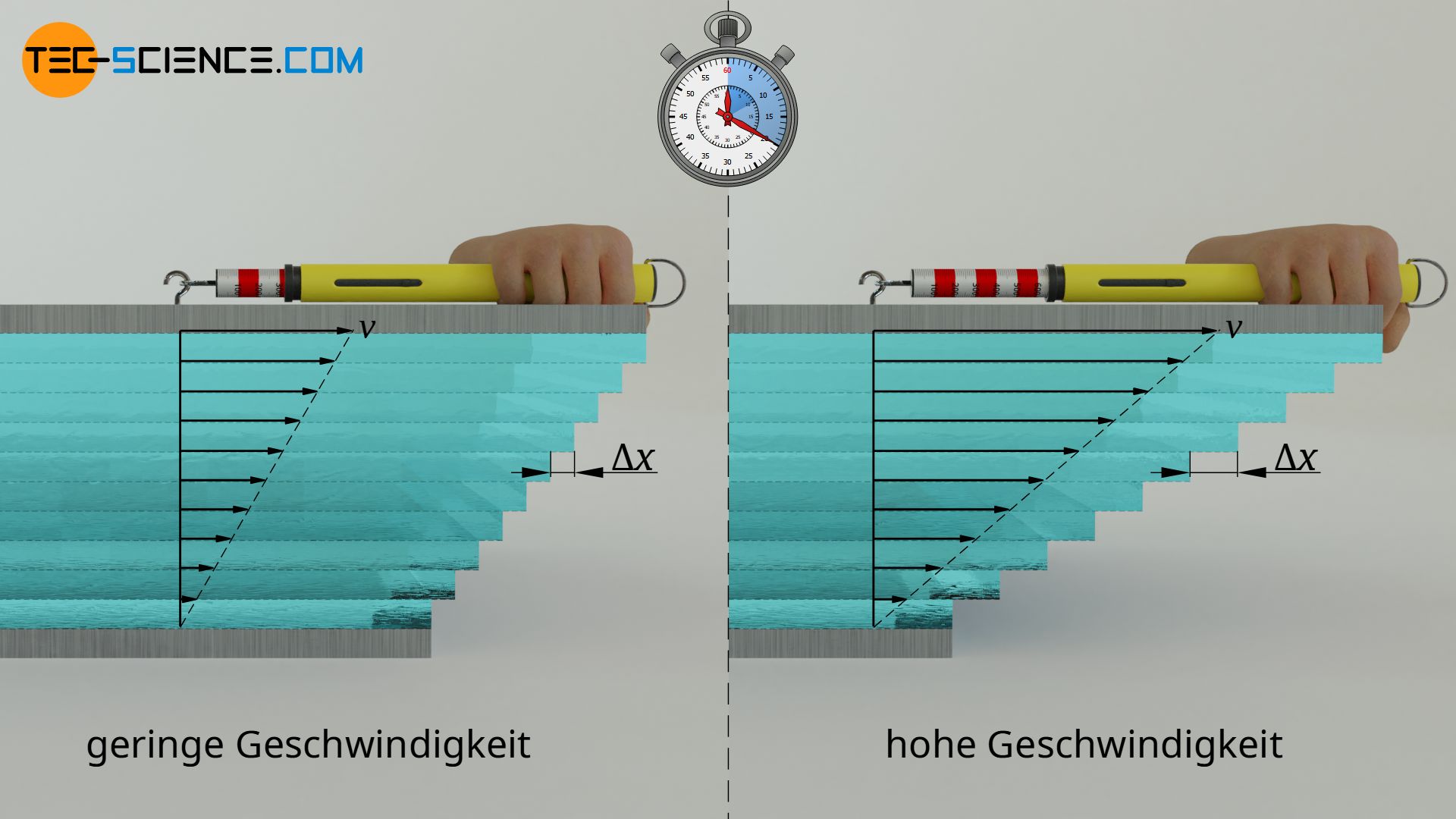
Als Kohäsion bezeichnet man Bindungskräfte innerhalb eines Stoffes, während Bindungskräfte zwischen zwei unterschiedlichen Stoffen als Adhäsion bezeichnet wird!

Theoretisch könnte sich zusätzlich zur oberen Platte auch die untere Platte mit einer bestimmten Geschwindigkeit bewegen. In diesem allgemeinen Fall, kommt es dann auf die Geschwindigkeitsdifferenz Δv der beiden Platten an, die die Kraft F bestimmt. In gewissen Grenzen zeigt sich dabei ein proportionaler Zusammenhang:

\begin{align}
& F \sim \Delta v \\[5px]
\end{align}

Einfluss des Abstandes der Platten (Dicke der Fluidschicht)

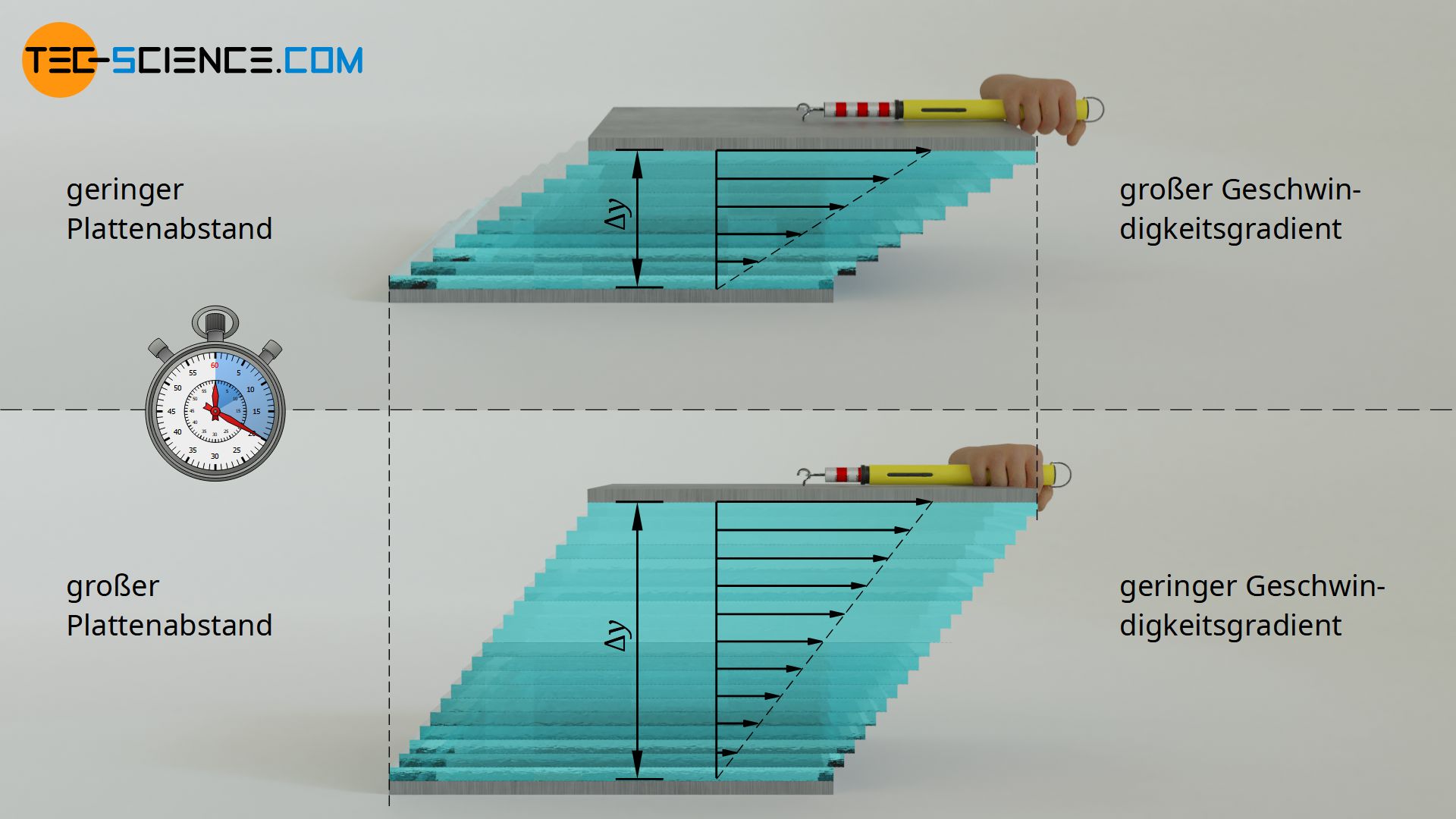
Die Stärke der Verschiebung und damit der Kraft, ist aber nicht nur durch die Geschwindigkeitsdifferenz bestimmt, sondern auch durch den Abstand der Platte. Je größer der Abstand bei gegebener Geschwindigkeitsdifferenz, desto geringer ist die Verschiebung der einzelnen Fluidschichten pro Zeiteinheit. Dabei gilt ein umgekehrt proportionaler Zusammenhang zwischen Plattenabstand Δy und Verschiebung bzw. Kraft F:

\begin{align}
& F \sim \frac{1}{\Delta y} \\[5px]
\end{align}

Einfluss der Plattenfläche

Als letztes beeinflusst noch die Plattenfläche bzw. die Fläche der Fluidschichten die benötigte Kraft. Umso größer die Fläche, desto mehr Bindungen sind offensichtlich zwischen den einzelnen Fluidschichten vorhanden und umso mehr Kraft wird benötigt, um die Fluidschichten entgegen diesen Bindungskräften zu verschieben. Benötigt Kraft F und Fläche A sind dabei proportional zueinander, denn schließlich bedeutet eine doppelt so große Fläche auch eine doppelte so hohe Anzahl an Bindungen:

\begin{align}
& F \sim A \\[5px]
\end{align}

Newtonsches Reibungsgesetz

Die benötigte Kraft F zur Verschiebung der Fluidschichten, ist also proportional zur Geschwindigkeitsdifferenz Δv und zur Plattenfläche A, sowie umgekehrt proportional zur Dicke der Fluidschicht Δy. Somit gilt für die benötigte Kraft folgender qualitativer Zusammenhang:

\begin{align}
& F \sim A \cdot \frac{\Delta v}{\Delta y}\\[5px]
& \underbrace{\frac{F}{A}}_{\tau} \sim \underbrace{\frac{\Delta v}{\Delta y}}_{\dot \gamma}\\[5px]
&\tau \approx \dot \gamma \\[5px]
\end{align}

Der Quotient auf der linken Seite der Gleichung beschreibt die Kraft pro Flächeneinheit, die benötigt wird, um die Fluidschichten gegeneinander abzuscheren bzw. aufeinander abzugleiten. Diese Größe wird deshalb auch Scherspannung τ genannt. Der Quotient auf der rechten Seite beschreibt die Geschwindigkeitsänderung im Fluid pro Längeneinheit (senkrecht zur Bewegungsrichtung), d.h. den sogenannten Geschwindigkeitsgradienten. Dieser Geschwindigkeitsgradient wird häufig auch als Schergeschwindigkeit γ* bezeichnet, da dieser sozusagen die Geschwindigkeit beschreibt mit der sich die einzelnen Schichten relativ zueinander verschieben.

\begin{align}
&\boxed{\tau:=\frac{F}{A}} ~~~\text{ Scherspannung} \\[5px]
&\boxed{\dot\gamma:=\frac{\Delta v}{\Delta y}} ~~~\text{ Schergeschwindigkeit (Geschwindigkeitsgradient)} \\[5px]
\end{align}

Die benötigte Scherspannung zur inneren Verschiebung des Fluids ist also proportional zur Schergeschwindigkeit. Der Proportionalitätsfaktor zwischen diesen Größen wird schließlich (dynamische) Viskosität η genannt. Die Einheit der Viskosität lautet Pa·s (Pascalsekunde), wobei für Flüssigkeiten und Gase aufgrund der geringen Viskositäten meist die Einheit mPa·s (Millipascalsekunde) verwendet wird. Man bezeichnet den proportionalen Zusammenhang zwischen Schergeschwindigkeit und Scherspannung auch als das Newtonsches Reibungsgesetz. Fluide die dieser Gesetzmäßigkeit folgen werden Newtonsche Fluide genannt (später dazu mehr).

\begin{align}
\label{t}
&\boxed{\tau= \eta \cdot \dot \gamma} ~~~[\eta]=\frac{\text{N}\cdot\text{s}}{\text{m²}}=\text{Pa}\cdot\text{s} ~~~~~\text{Newtonsches Reibungsgesetz}\\[5px]
\end{align}

Höhere Viskositätswerte bedeuten folglich größere benötigte Scherspannungen, um die Fluidschichten gegeneinander abzuscheren und umso größer ist der innere Fließwiderstand.

Die (dynamische) Viskosität beschreibt den mathematischen Zusammenhang zwischen der Schergeschwindigkeit und Scherspannung. Man bezeichnet dies auch als das Newtonsche Reibungsgesetz.

Die Definition der Viskosität setzt voraus, dass die Bewegung des Fluids in einzelnen Schichten aufgeteilt werden kann, die sich gegeneinander verschieben. Man spricht bei einer solchen Schichtenströmung auch von einer laminaren Strömung. Bei hohen Strömungsgeschwindigkeiten bilden sich im Fluid jedoch Verwirbelungen und die Strömung wird turbulent. In diesem Fall macht die Definition einer Viskosität jedoch keinen Sinn. Die Aussagekraft der Viskosität bleibt somit auf laminare Strömungen beschränkt. Mehr Informationen zu laminaren und turbulenten Strömungen finden sich im Artikel Reynolds-Zahl (laminare und turbulente Strömung).

Temperaturabhängigkeit der Viskosität

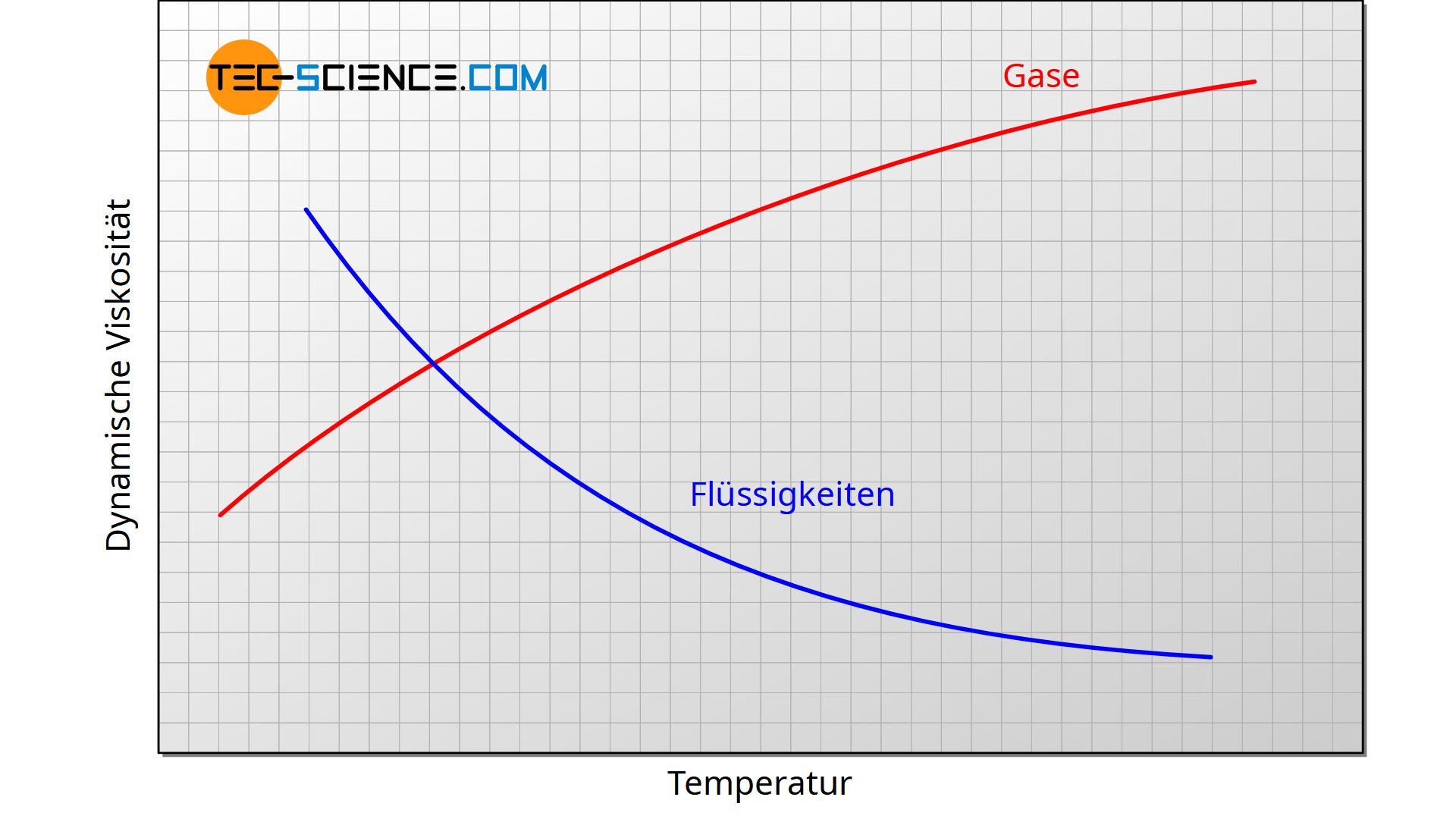
Die Viskosität ist im Allgemeinen druck- und vor allem temperaturabhängig. Bei Flüssigkeiten nimmt die Viskosität mit zunehmender Temperatur ab. Sehr anschaulich zeigt sich dieses Verhalten bspw. bei Honig oder Butter. Werden diese Stoffe erwärmt, dann werden sie deutlich fließfähiger, d.h. die Viskosität nimmt ab. Aber auch Wasser zeigt eine ausgeprägte Temperaturabhängigkeit. So besitzt Wasser bspw. bei 5° eine Viskosität von 1,5 mPa·s, bei 20 °C hat sich die Viskosität um ein Drittel auf 1,0 mPa·s verringert.

Anschaulich erklärt werden kann dieses Verhalten mit der Vergrößerung der Atomabstände aufgrund der Wärmeausdehnung, die mit einer Temperaturerhöhung einhergeht. Nehmen die Atomabstände infolge einer Temperaturerhöhung zu, dann nehmen die intermolekularen Anziehungskräfte ab. Man kann sich die Situation mit zwei Magneten veranschaulichen. In geringem Abstand ziehen sich die Magneten relativ stark an. Mit zunehmendem Abstand werden die Anziehungskräfte geringer. Zwar handelt es sich bei Atomen nicht um magnetische Kräfte, sondern um elektrostatische Anziehungskräfte, jedoch sind die Gesetzmäßigkeiten in beiden Fällen ähnlich. Übertragen auf die Atome eines Fluids bedeutet dies, dass sich die Fluidschichten mit zunehmendem Molekülabstand nicht mehr so stark aneinanderhaften.

Für Newtonsche Fluide, kann die Temperaturabhängigkeit in guter Näherung meist durch eine exponentielle Funktion beschrieben werden. Dies gilt prinzipiell auch für die Druckabhängigkeit, die jedoch erst bei hohen Drücken eine merkliche Rolle spielt. Für die Temperaturabhängigkeit gilt in guter Näherung die nachfolgend angegebene Gleichung. Darin bezeichnet η₀ eine fiktive Bezugsviskosität und a und b Konstanten, sowie T die Temperatur (siehe H. Vogel: Das Temperaturabhängigkeitsgesetz der Viskosität von Flüssigkeiten. 1921).

\begin{align}
&\boxed{\eta(T) \approx \eta_0 \cdot \text{e}^{\left( \LARGE \frac{a}{T+b}\right)}}~~~\text{für Flüssigkeiten} \\[5px]
\end{align}

Bei Gasen zeigt sich meist ein anderer Zusammenhang zwischen Viskosität und Temperatur. Bei diesen Stoffen nimmt die Viskosität im Allgemeinen mit steigender Temperatur zu. Dies ist dem verstärkten Impulsaustausch zwischen den einzelnen Gasschichten geschuldet, der neben den intermolekularen Anziehungskräften ebenfalls die Viskosität bestimmt. Bei Flüssigkeiten spielt dieser Impulsaustausch eine untergeordnete Rolle, weshalb dieser nicht entscheidend die Viskosität von Flüssigkeiten beeinflusst. Ausführlichere Informationen hierzu finden sich im Artikel Viskosität eines idealen Gases.

Für Gase kann die Abhängigkeit der Viskosität mit nachfolgend angegebener Gleichung beschrieben werden. Darin η₀ die Bezugs-Viskosität bei einer Bezugs-Temperatur T₀ und c eine stoffabhängig Sutherland-Konstante (siehe W. Sutherland: The Viscosity of Gases and Molecular Force. 1893).

\begin{align}
&\boxed{\eta(T) \approx \eta_0 \cdot \frac{T_0+c}{T+c}\cdot \left(\frac{T}{T_0}\right)^\frac{3}{2}}~~~\text{für Gase} \\[5px]
\end{align}

Gebrauchsformeln zur Berechnung der Viskosität von Luft und Wasser

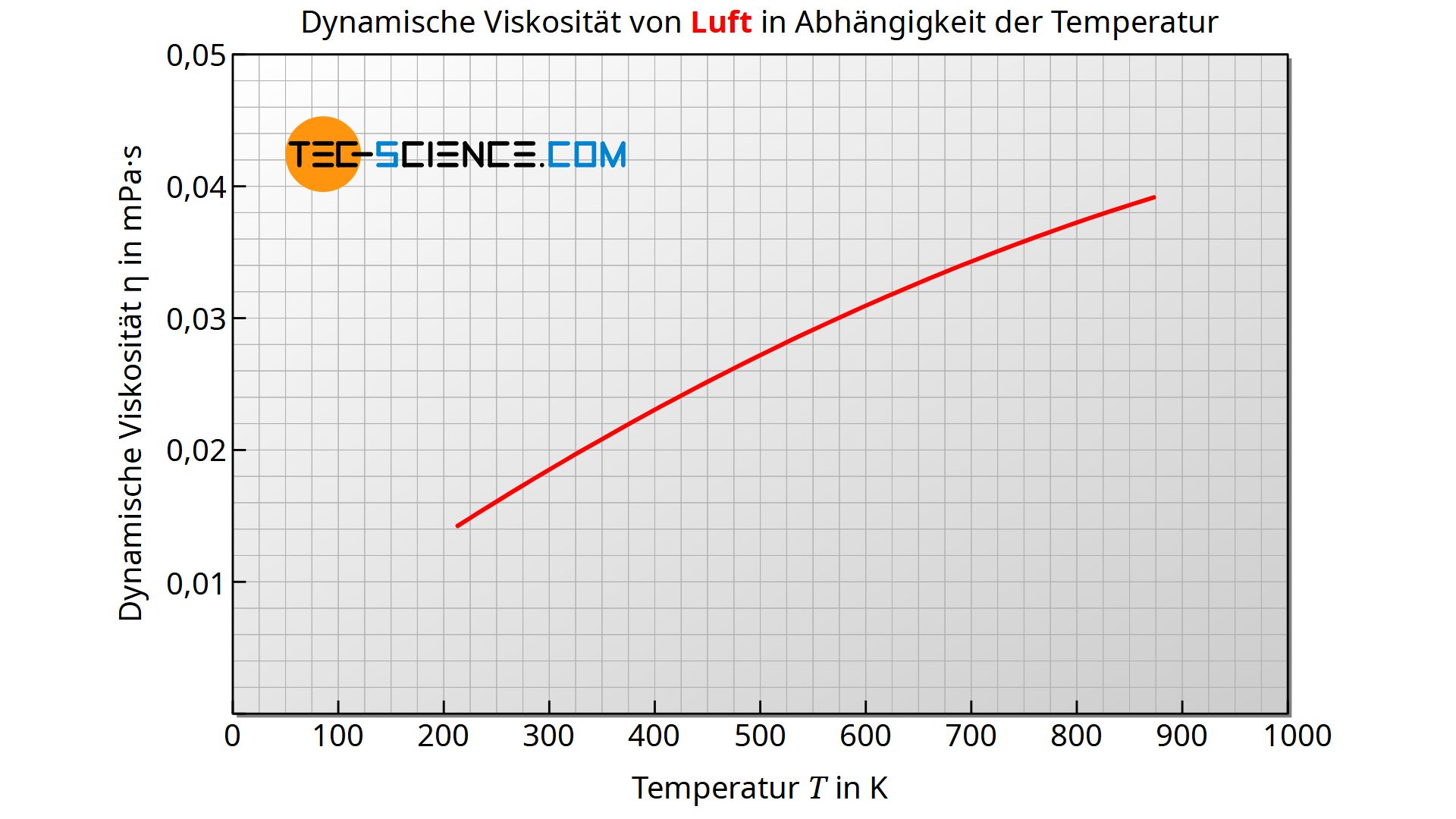
In vielen Fällen praktischen Fällen, handelt es sich bei den strömenden Fluiden um Luft (z.B. in Windkanälen) oder um Wasser (z.B. in Rohrleitungen). Für Luft bei 1 bar Druck kann die dynamische Viskosität im Temperaturbereich zwischen -20 °C und 400 °C in guter Näherung mit nachfolgend angegebener Formel ermittelt werden. Die Abweichungen zu den Literaturwerten betragen weniger als 1 %. Die Temperatur ist dabei in der Einheit Kelvin einzusetzen, um die Viskosität in der Einheit Pa·s zu berechnen.

\begin{align}
&\boxed{\eta_{\text{Luft}}(T) = 2,791\cdot 10^{-7} \cdot T^{0,7355}}~~~\text{in Pa·s} \\[5px]
\end{align}

Die dynamische Viskosität von Wasser bei 1 bar Druck kann im Temperaturbereich zwischen 0 °C und 100 °C mit einer Abweichung von weniger als 1 % zu den Literaturwerten mit unten angegebener Formel bestimmt werden. Die Temperatur ist dabei wieder in der Einheit Kelvin einzusetzen, sodass das Ergebnis in der Einheit Pa·s ausgegeben wird.

\begin{align}
&\boxed{\eta_{\text{Wasser}}(T) = \frac{1}{0,1\cdot T^2-34,335 \cdot T+2472}}~~~\text{in Pa·s} \\[5px]
\end{align}

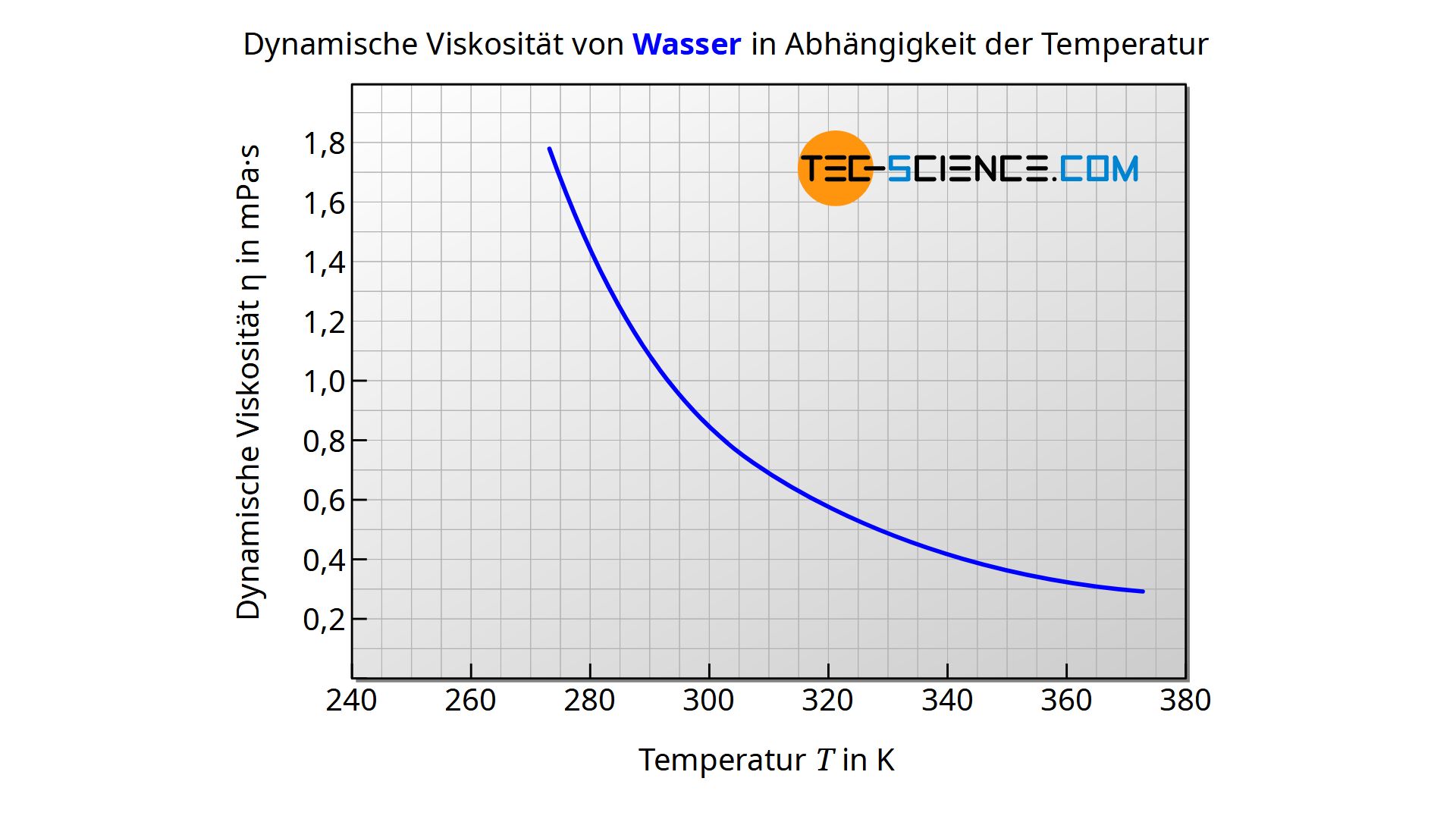
Die abnehmende Viskosität bei erhöhter Temperatur kann man im Falle von Wasser sogar „hören“! Gießt man kaltes Wasser in ein Glas ist der Ton deutlich höher als bei heißem Wasser. Ursache ist die geringere Viskosität des heißen Wassers, die zu größeren Blasen beim Eingießen führt. Die Größe dieser Blasen beeinflusst wiederum den Ton, sodass sich kaltes Wasser mit höherer Viskosität hörbar von heißem Wasser mit geringerer Viskosität unterscheidet.

Dynamische und kinematische Viskosität

Wenn von der Viskosität die Rede ist, dann ist damit meist die dynamische Viskosität η gemeint, wie sie im Abschnitt zuvor definiert worden ist. Die Fließeigenschaften von Flüssigkeiten oder Gasen werden aber nicht nur durch die Viskosität eines Fluids bestimmt, sondern auch durch dessen Dichte. Für die Charakterisierung des Fließverhaltens ist es deshalb sinnvoll die Viskosität in Relation zur Dichte zu betrachten. Wird die Viskosität auf die Dichte des Fluids bezogen, dann spricht man auch von kinematischen Viskosität ν (Griechischer Kleinbuchstabe Nu). Die Einheit der kinematischen Viskosität lautet m²/s.

\begin{align}
&\boxed{\nu= \frac{\eta}{\rho}} ~~~\text{ kinematische Viskosität} ~~~[\nu]=\frac{\text{m²}}{\text{s}} \\[5px]
\end{align}

Die kinematische Viskosität setzt die Viskosität eines Fluids ins Verhältnis zu dessen Dichte und ist ein Maß für die Zähigkeit eines Fluids. Sie ermittelt sich aus dem Quotienten von dynamischer Viskosität und Dichte!

Eine hohe kinematische Viskosität bedeutet, dass das Fluid im Vergleich zu seiner Dichte eine sehr große Viskosität besitzt. Umgangssprachlich würde man sagen, dass sich das Fluid relativ zähflüssig verhält. Im Gegensatz zur dynamischen Viskosität als Maß für den inneren Fließwiderstand, kann die kinematische Viskosität salopp formuliert als Zähigkeit aufgefasst werden. Im Gegensatz zur dynamischen Viskosität ist die kinematische Viskosität auch bei geringen Drücken relativ stark vom Druck abhängig, vor allem bei kompressiblen Stoffen die eine ausgeprägte Druckabhängigkeit zeigen wie bspw. Gase.

Wie bereits angedeutet spielt diese Zähigkeit bzw. die kinematische Viskosität eine große Rolle, wenn es um die Fließeigenschaften eines Fluids geht. Sie entscheidet nämlich maßgeblich darüber, wie anfällig eine strömendes Fluid gegenüber Verwirbelungen ist. Sie hat somit großen Einfluss darauf ab welcher Geschwindigkeit ein Fluid von der laminare Strömung in die turbulente Strömung übergeht (siehe Artikel Reynolds-Zahl (laminare und turbulente Strömung)).

Anmerkung zu den Begrifflichkeiten: Die kinematische Viskosität beschreibt das Fließverhalten, d.h. die Kinematik der Strömung. Die dynamische Viskosität hingegen beschreibt die wirkenden Kräfte, d.h. die Dynamik der Strömung.

Newtonsche und Nicht-Newtonsche Fluide

Bei vielen Fluiden ist die Viskosität in sehr guter Näherung tatsächlich eine Stoffkonstante, die nur temperatur- und druckabhängig ist. Die Viskosität und damit das Fließverhalten ist für solche Newton’schen Fluide unabhängig der Schergeschwindigkeit. In einem Diagramm, welches den Zusammenhang zwischen Scherspannung und Schergeschwindigkeit zeigt, erhält man in diesen Fällen eine Ursprungsgerade. Die Steigung dieser Gerade entspricht nach Gleichung (\ref{t}) gerade der Viskosität des Fluids und diese ist in jedem Punkt konstant. Wasser, Gase und viele Öle zeigen ein solches newtonsches Fließverhalten.

Bei Newtonschen Fluiden ist das Fließverhalten (Viskosität) unabhängig der Schergeschwindigkeit konstant!

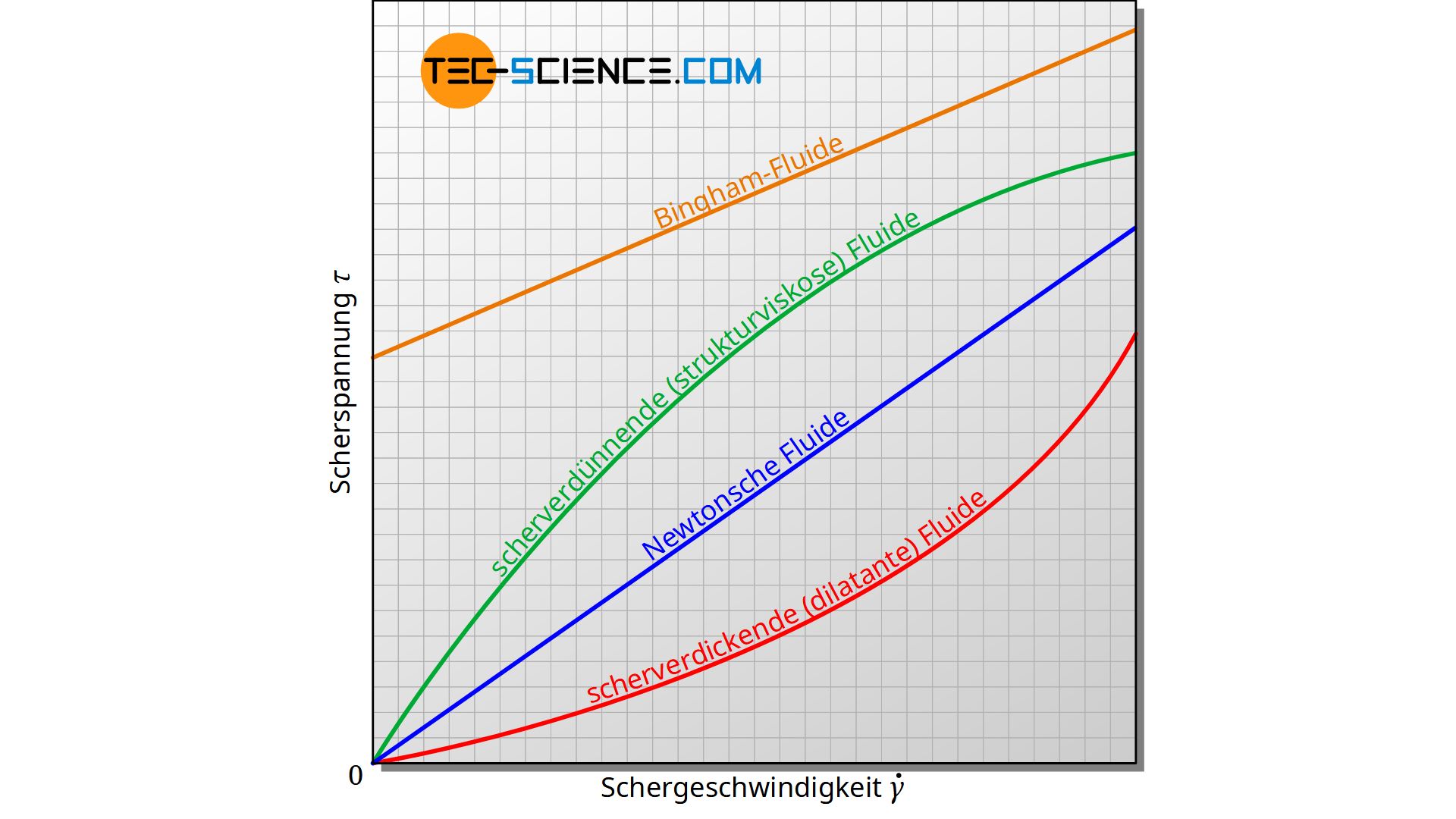
Es gibt aber auch Fluide, deren Viskosität von der Schergeschwindigkeit abhängt. Das Fließverhalten solcher nicht-Newtonschen Fluide ändert sich je nach Schergeschwindigkeit. Blut, Ketchup und Zahnpasta zählen bspw. hierzu. Da die Viskosität für solche Stoffe keine Konstante mehr ist, kann auch das Fließverhalten nicht mehr mit Gleichung (\ref{t}) beschrieben werden. Hierzu zählen die nachfolgend erläuterten Fluide.

Scherverdickende (dilatante) Fluide

Nimmt der Fließwiderstand eines Fluids mit steigender Schergeschwindigkeit zu, dann verhält sich das Fluid sozusagen dickflüssiger. Man spricht deshalb von einem scherverdickenden Fluid. Ein solches Fluid wird auch als dilatantes Fluid bezeichnet (lat. dilatus = „verzögern“). Das zunehmend viskosere Fließverhalten eines solchen Fluids zeigt sich im Diagramm als eine immer steiler ansteigende Kurve.

Scherverdickende (dilatante) Fluide zeigen mit zunehmender Schergeschwindigkeit eine Zunahme des Fließwiderstandes!

Ein dilatentes Medium kann man Zuhause relativ einfach selbst herstellen. Hierzu gibt man zu etwa 3 Teilen Stärke ungefähr 2 Teile Wasser hinzu und verrührt dies gut. Fährt man nun mit einem Löffel langsam durch den erhaltenen Stärke-Wasser-Brei (geringe Schergeschwindigkeit), so verhält sich die Mischung relativ flüssig. Versucht man den Löffel allerdings sehr schnell durch die Mischung zu bewegen (hohe Schergeschwindigkeit), dann verdickt dieser und beginnt teilweise auch wie ein Festkörper zu bröseln. Die weggebröselten Teilen verflüssigen sich anschließend wieder.

Mathematisch beschrieben werden kann die Dilatanz mit nachfolgendem Ansatz. Darin bezeichnen K und n Konstanten, wobei der Fließindex n in diesem Fall größer 1 ist.

\begin{align}
\label{d}
&\boxed{\tau= K \cdot \left(\frac{\text{d}v}{\text{d}y}\right)^n} \\[5px]
\end{align}

Scherverdünnende (strukturviskose) Fluide

Umgekehrt spricht man von einem scherverdünnenden Fluid, wenn sich das Fluid mit zunehmender Schergeschwindigkeit dünnflüssiger verhält, d.h. die Viskosität abnimmt. Ein solches Fluid wird auch als strukturviskoses Fluid bezeichnet. Im Diagramm verläuft die Kurve eines solchen Fluids immer flacher.

Scherverdünnende (strukturviskose) Fluide zeigen mit zunehmender Schergeschwindigkeit eine Abnahme des Fließwiderstandes!

Ein Beispiel für ein strukturviskoses Fluid ist bspw. Treibsand. Dies macht Treibsand auch so gefährlich, denn unter Panik bei schnellen Bewegungen verdünnt sich die Wasser-Sand-Mischung und man sinkt immer schnelle ein. In diesem Fall ist es als besser, sich so ruhig wie möglich zu verhalten und nur langsame Bewegungen zu machen. Auch Blut zählt im Übrigen zu den scherverdünnenden Fluiden.

Auch das Fließverhalten von strukturviskosen Fluiden kann mit Gleichung (\ref{d}) beschrieben werden, wobei in diesen Fällen der Fließindex n kleiner 1 ist. Im Übrigen gilt diese Gleichung auch für Newtonsche Flüssigkeiten mit einem Fließindex von n und K als dynamische Viskosität!

Bingham-Fluide

Es gibt aber auch Fluide, die überhaupt erst eine bestimmte Mindest-Scherspannung benötigen, damit die Fluidschichten abscheren. Unterhalb dieser Mindestspannung setzt kein Fließverhalten ein. Solche Fluide werden auch als Bingham-Fluid bezeichnet. Beispiele hierfür sind Zahnpasta, Mayonnaise oder Ketchup.

Bingham-Fluide benötigen eine Mindest-Scherspannung, um ein Fließen des Fluids zu erreichen!

Bei einer Zahnpasta wird ein solches nicht-newtonsches Fließverhalten sehr anschaulich. Stellt man die Zahnpastatube auf den Kopf, dann läuft diese nicht von selbst aus der Öffnung. Man benötigt erst eine gewissen Mindestkraft durch Drücken auf die Tube, damit die Zahnpasta aus der Öffnung fließt. Auch beim Versuch Ketchup aus einer Glasflasche zu bekommen, zeigt sich, dass das bloße Umdrehen der Flasche in der Regel nicht ausreicht. Man muss mit der Hand zunächst auf den Boden der Flasche klopfen, d.h. eine Mindest-Scherspannung aufbringen, um den Fließvorgang in Gang zu bringen.

Bingham-Fluide lassen im Diagramm als Kurve mit einem entsprechenden y-Achsenabschnitt τ₀ (Mindest-Scherspannung) darstellen. Sie können durch folgende Gleichung beschrieben werden, mit n als Fließindex (n=1 für eine Gerade):

\begin{align}
\label{b}
&\boxed{\tau= K \cdot \left(\frac{\text{d}v}{\text{d}y}\right)^n + \tau_0} \\[5px]
\end{align}