Die Wärmeleitungsgleichung beschreibt für die Wärmeleitung das zeitliche und räumliche Verhalten der Temperatur.
Herleitung der Wärmeleitungsgleichung
Wir betrachten zunächst den eindimensionalen Fall der Wärmeleitung. Dieser lässt sich mit einem langen dünnen Stab in sehr guter Näherung erzielen. Dabei gehen wir davon aus, dass Wärme nur entlang des Stabes übertragen wird und nicht seitlich auf die Umgebung übergeht. Der Stab ist sozusagen ideal wärmegedämmt.

Zudem werden die Stoffgrößen des homogenen Stabes wie Wärmekapazität und Dichte als konstant betrachtet. Nun wird der Stab an einer Stelle oder auch an mehreren Stellen erhitzt. Hieraufhin strömt Wärme von Stellen höherer Temperatur zu Stellen mit niedrigeren Temperaturen. Heiße Stellen werden folglich kälter und kühlere Stellen heißer, bis sich irgendwann die Temperaturen angeglichen haben und der Stab eine einheitliche und zeitlich konstante Temperatur aufweist.
Wir betrachten während der Temperaturangleichung nun an einer beliebigen Stelle einen infinitesimalen Streckenabschnitt dx. Dieser Abschnitt ändere durch die zu- oder abgeführte Wärme Qn seine Temperatur innerhalb der Zeit dt um den Wert dT. Zwischen der Wärme Qn und der Temperaturänderung dT besteht folgender Zusammenhang (mit c als spezifische Wärmekapazität):
\begin{align}
&Q_n = m \cdot c \cdot \text{d}T \\[5px]
&Q_n = \underbrace{\overbrace{A \cdot \text{d}x}^{V} \cdot \rho}_{m} \cdot c \cdot \text{d}T \\[5px]
\end{align}
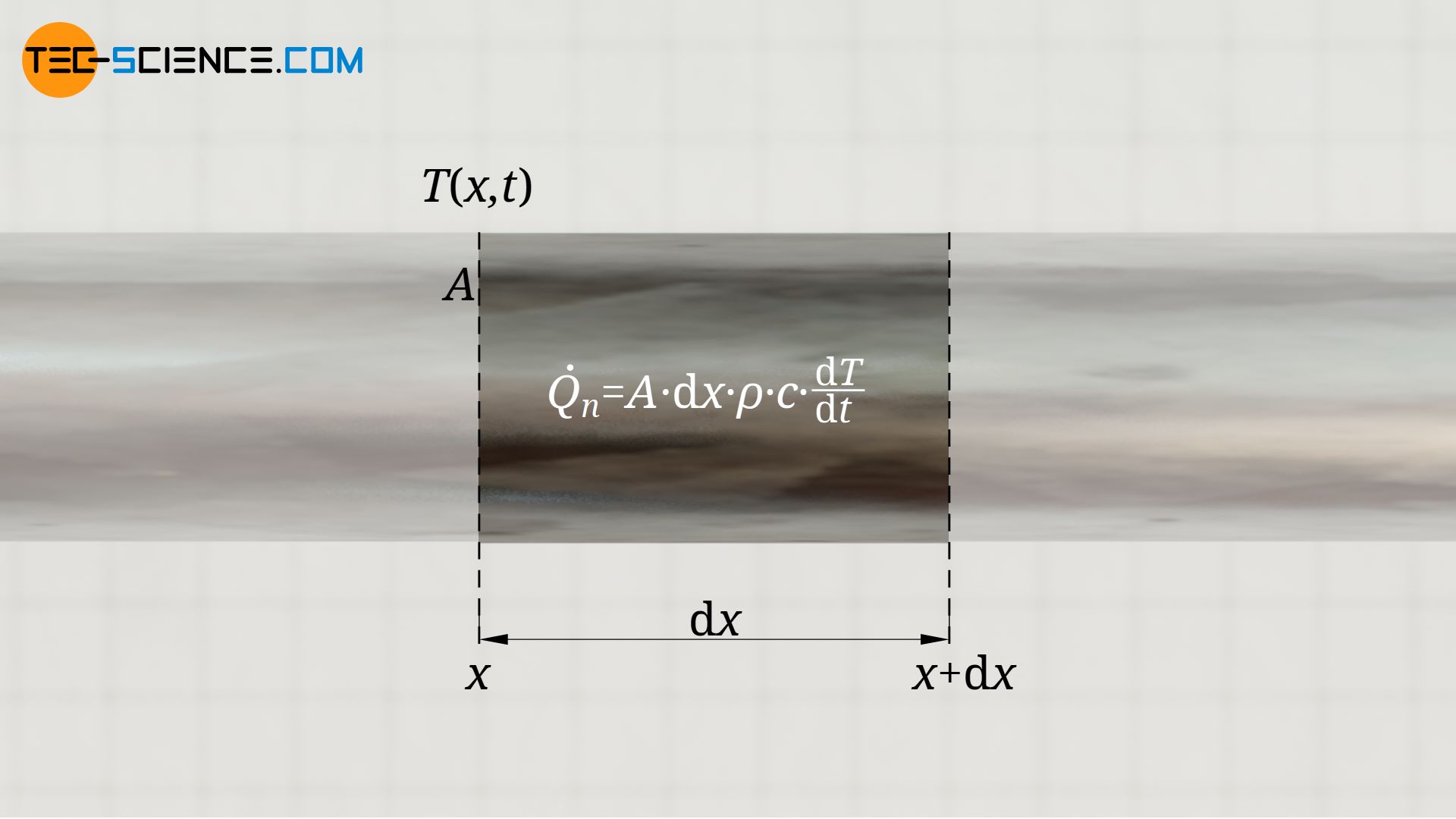
In der oberen Gleichung wurde die Masse m des Stababschnitts durch sein Volumen V und seine Dichte ϱ ausgedrückt, wobei das Volumen wiederum durch die Fläche A und den betrachteten Streckenabschnitt dx beschrieben werden kann.
Da die Wärme Qn innerhalb der Zeit dt übertragen wird, gilt zwischen dem insgesamt zu- oder abgeführten Wärmestrom Q*n=Qn/dt und der zeitlichen Änderung der Temperatur dT/dt folgender Zusammenhang:
\begin{align}
&\frac{Q_n}{\text{d}t} = A \cdot \text{d}x \cdot \rho \cdot c \cdot \frac{\text{d}T}{\text{d}t} \\[5px]
\label{Q}
&\dot Q_n = A \cdot \text{d}x \cdot \rho \cdot c \cdot \frac{\text{d}T}{\text{d}t} \\[5px]
\end{align}
In der oberen Gleichung beschreibt Q*n sozusagen den Netto-Wärmestrom, der dem betrachteten Abschnitt für den Fall einer Erwärmung insgesamt zugutekommt oder im Falle einer Abkühlung insgesamt entzogen wird (deshalb auch der Index „n“). Diese Gleichung beschreibt letztlich die Auswirkung eines Wärmestroms auf das zeitliche Temperaturverhalten, nicht aber die Ursache des Wärmestroms selbst. Die Ursache eines Wärmestrom ist das Vorhandensein eines Temperaturgradienten dT/dx gemäß des Fourier’schen Gesetzes (mit λ als Wärmeleitfähigkeit):
\begin{align}
\label{f}
&\underline{\dot Q = – \lambda \cdot A \cdot \frac{\text{d}T}{\text{d}x}} ~~~~~\text{Fourier’sches Gesetz} \\[5px]
\end{align}
Man kann den Netto-Wärmestrom des betrachteten Abschnittes wie folgt bestimmen. Man muss mit Hilfe des Fourier’schen Gesetzes zum einen ermitteln, welcher Wärmestrom Q*ein in den Abschnitt hineinführt, und zum anderen welcher Wärmestrom Q*aus aus dem Abschnitt wieder heraustritt. Die Differenz hiervon entspricht dann schließlich dem Netto-Wärmestrom. Der Netto-Wärmestrom ist somit nichts anderes als die infinitesimale Differenz dQ* in den Wärmeströmen zischen Ein- und Austritt:
\begin{align}
&\dot Q_n = \dot Q_{\text{aus}} – \dot Q_{\text{ein}} = {\text{d}\dot Q} \\[5px]
\end{align}
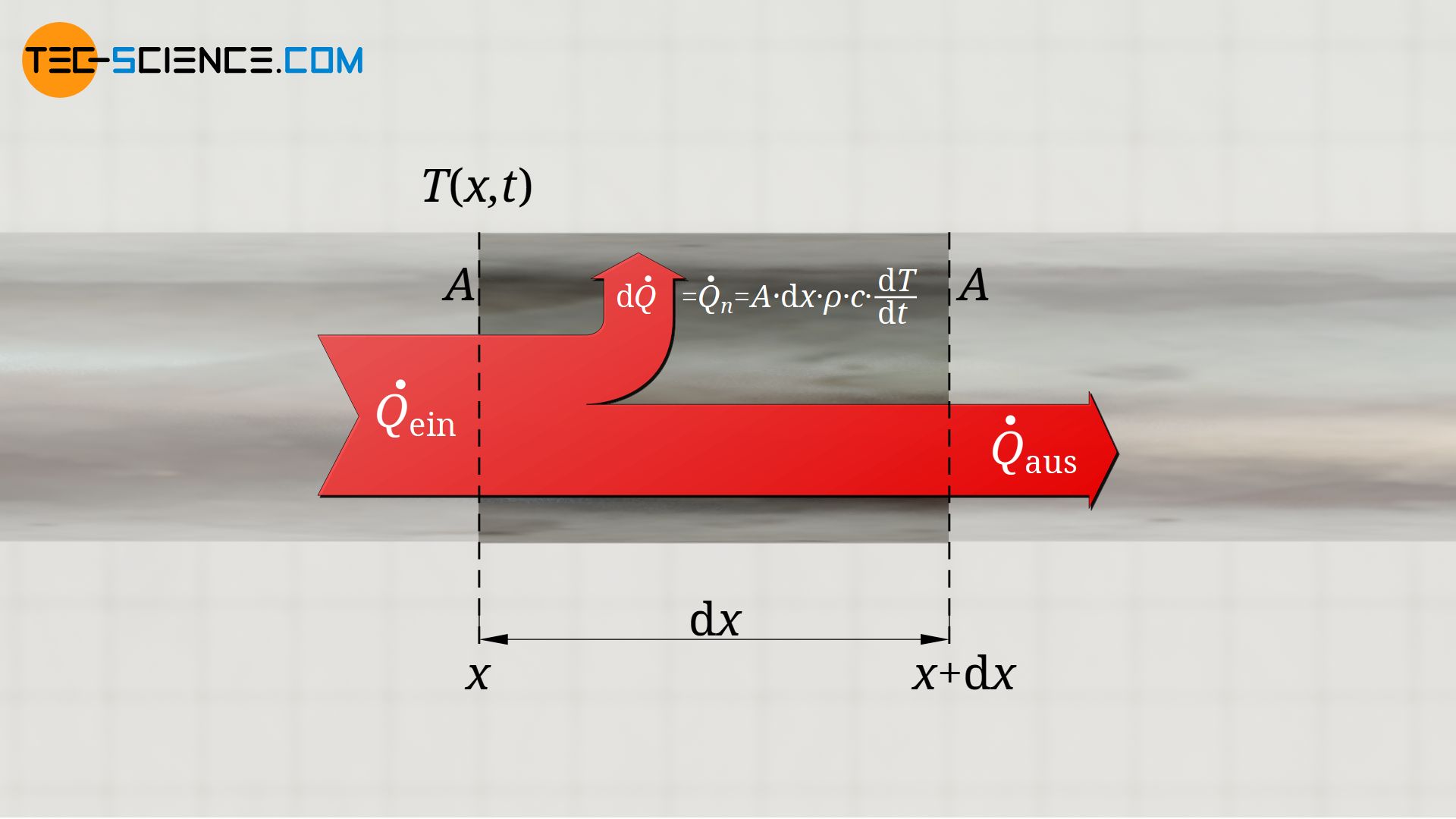
An dieser Stelle muss für eine korrekte mathematische Beschreibung beachtet werden, dass eine Vergrößerung des Wärmestroms entlang der (positiven) x-Richtung des Stabes bedeutet, dass der austretende Wärmestrom größer ist als der eintretende Wärmestrom. Demzufolge wird dem betrachteten Abschnitt Wärme entzogen. Diese Wärme ist negativ zu zählen ist, damit die Temperaturänderung gemäß Gleichung (\ref{Q}) auch tatsächlich einer Abnahme der Temperatur entspricht (dT<0). Somit gilt für den mathematisch korrekten Zusammenhang:
\begin{align}
&\underline{\dot Q_n =- {\text{d}\dot Q}} \\[5px]
\end{align}
Ersetzt man in Gleichung (\ref{Q}) den Netto-Wärmestrom Q*n also durch die Differenz des aus- und eintretenden Wärmestroms dQ*, dann gilt für die zeitliche Änderung der Temperatur folgender Zusammenhang:
\begin{align}
\label{kor}
&-\text{d} \dot Q = A \cdot \text{d}x \cdot \rho \cdot c \cdot \frac{\text{d}T}{\text{d}t} \\[5px]
& \frac{\text{d}T}{\text{d}t} =- \frac{1}{A \cdot \rho \cdot c} \cdot \frac{\text{d} \dot Q}{\text{d}x} \\[5px]
\end{align}
Der Term dQ*/dx entspricht der Ableitung des Wärmestroms nach dem Ort (Wärmestromgradient). Gemäß des Fourier’schen Gesetzes entspricht dies dann wiederum der zweiten Ableitung der Temperatur nach dem Ort. Durch Einsetzen des Fourier’schen Gesetzes (\ref{f}) in die obere Gleichung zeigt sich dies wie folgt:
\begin{align}
\require{cancel}
& \frac{\text{d}T}{\text{d}t} =- \frac{1}{A \cdot \rho \cdot c} \cdot \frac{\text{d} \dot Q}{\text{d}x} \\[5px]
& \frac{\text{d}T}{\text{d}t} =- \frac{1}{A \cdot \rho \cdot c} \cdot \frac{\text{d} \left( – \lambda \cdot A \cdot \frac{\text{d}T}{\text{d}x} \right)}{\text{d}x} \\[5px]
& \frac{\text{d}T}{\text{d}t} =- \frac{-\lambda \cdot \bcancel{A}}{\bcancel{A} \cdot \rho \cdot c} \cdot \frac{\text{d} \left(\frac{\text{d}T}{\text{d}x} \right)}{\text{d}x} \\[5px]
& \underline{\frac{\text{d}T}{\text{d}t} = \frac{\lambda}{\rho \cdot c} \cdot \frac{\text{d}^2 T}{\text{d}x^2}} \\[5px]
\end{align}
Die zeitliche Änderung der Temperatur an einem bestimmten Ort ist folglich durch die zweite örtliche Ableitung der Temperaturverteilung gegeben. Die zweifache örtliche Ableitung entspricht sozusagen der (örtlichen) Änderung des Temperaturgradienten in dem betrachteten Punkt.
Die zeitliche Änderung der Temperatur in einem bestimmten Punkt ergibt sich aus der örtlichen Änderung des Temperaturgradienten in diesem Punkt. Die Wärmeleitungsgleichung beschreibt insbesondere für den instationären Fall die Ausbreitung der Temperatur in einem Stoff.
Die Temperatur ist im Allgemeinen nicht nur eine Funktion der Zeit, sondern auch des Ortes, denn schließlich besitzt der Stab entlang seiner Länge unterschiedliche Temperaturen. In der oberen Gleichung handelt es sich deshalb auf der linken Seite der Gleichung um eine partielle Ableitung der Temperatur nach der Zeit und auf der rechten Seite der Gleichung um eine zweifache partielle Ableitung nach dem Ort. Die korrekte mathematische Schreibweise lautet somit wie folgt:
\begin{align}
&\boxed{\frac{\partial T(x,t)}{\partial t} = \frac{\lambda}{\rho \cdot c} \cdot \frac{\partial^2 T(x, t)}{\partial x^2}} \\[5px]
\end{align}
Es handelt sich bei dieser Differentialgleichung um eine sogenannte parabolische partielle Differentialgleichung zweiter Ordnung.
Erläuterung und Interpretation der Wärmeleitungsgleichung
Man kann sich die Aussage der Wärmeleitungsgleichung anschaulich verdeutlichen. Steigt der Temperaturgradient an einer Stelle nämlich stark an (positive Änderung des Temperaturgradienten ∂²T/∂x²>0), dann bedeutet dies nichts anderes als dass der Temperaturgradient an eine Stelle unmittelbar rechts davon größer ist. In diesem Fall strömt also sehr viel mehr Wärme von rechts in den betrachteten Abschnitt ein, als links wieder herausströmt. Beachte, dass der Wärmestrom stets in Richtung abnehmender Temperatur fließt; in diesem Fall also jeweils von rechts nach links.
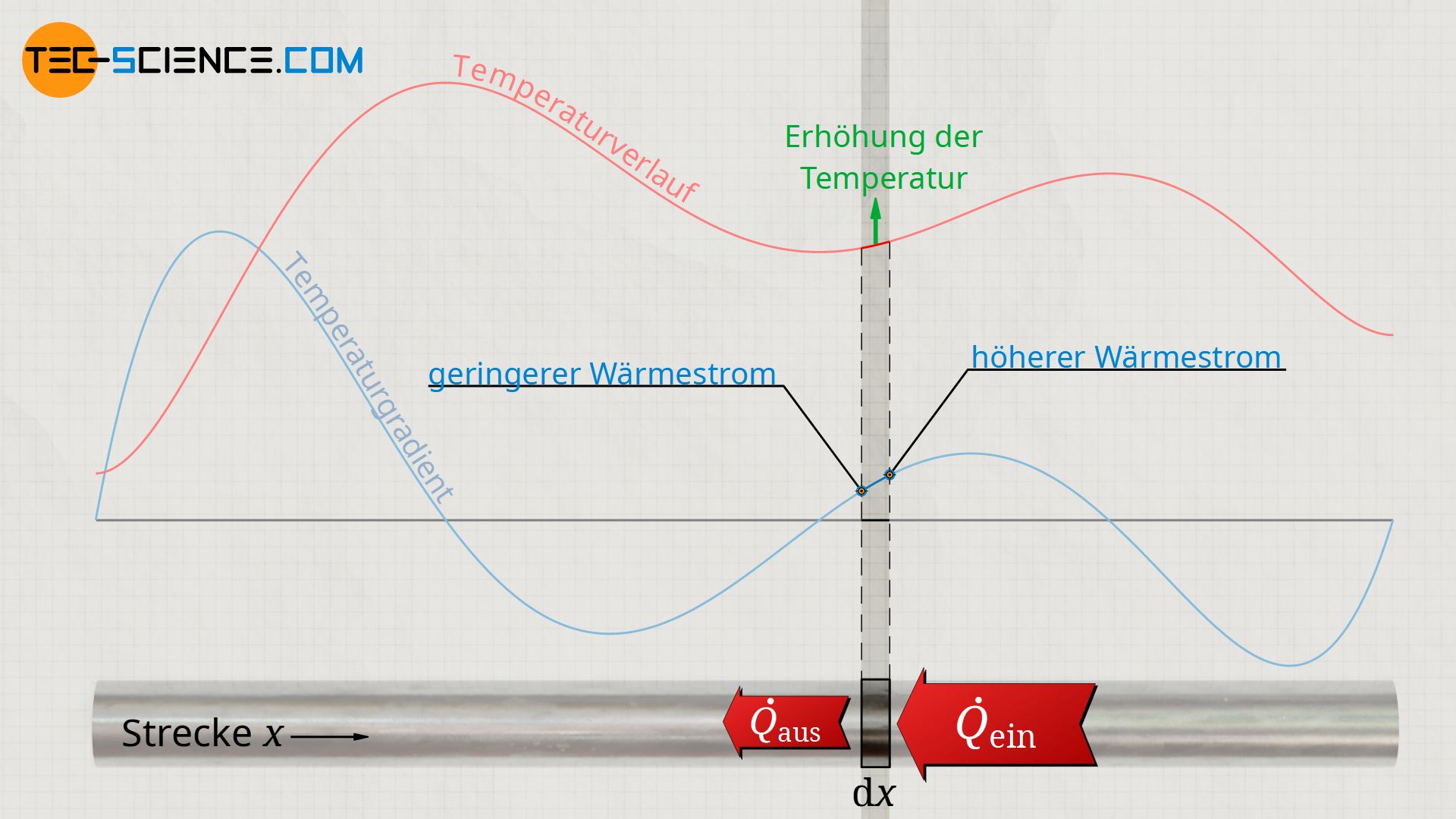
Die Temperatur nimmt in diesem Fall also im betrachteten Streckenabschnitt zeitlich zu. Umso stärker die Änderung des Temperaturgradienten dabei ist, stärker unterscheiden sich der eintretende Wärmestrom vom austretenden Wärmestrom. Dies resultiert in einem größeren Netto-Wärmestrom und damit einem zeitlich stärkeren Anstieg der Temperatur.
Nimmt hingegen der Temperaturgradient in einem Punkt ab (negative Änderung des Temperaturgradienten ∂²T/∂x²<0) , so zeigt sich etwas rechts dieses Punktes ein geringerer Temperaturgradient. In diesem Fall strömt weniger Wärme von rechts in den betrachteten Abschnitt ein, aber mehr Wärme auf der linken Seite wieder heraus. Die Temperatur nimmt also im betrachteten Streckenabschnitt zeitlich ab.
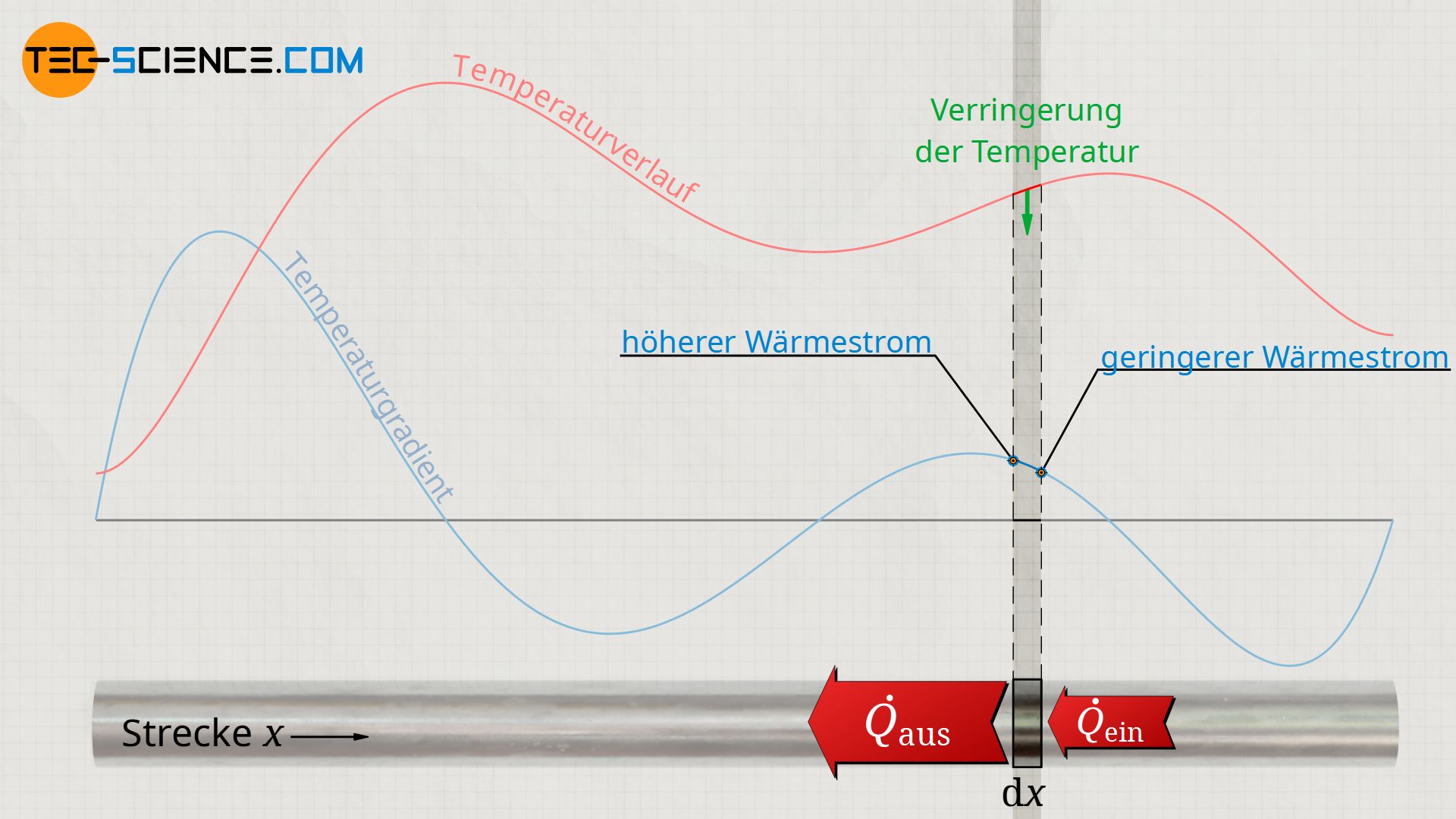
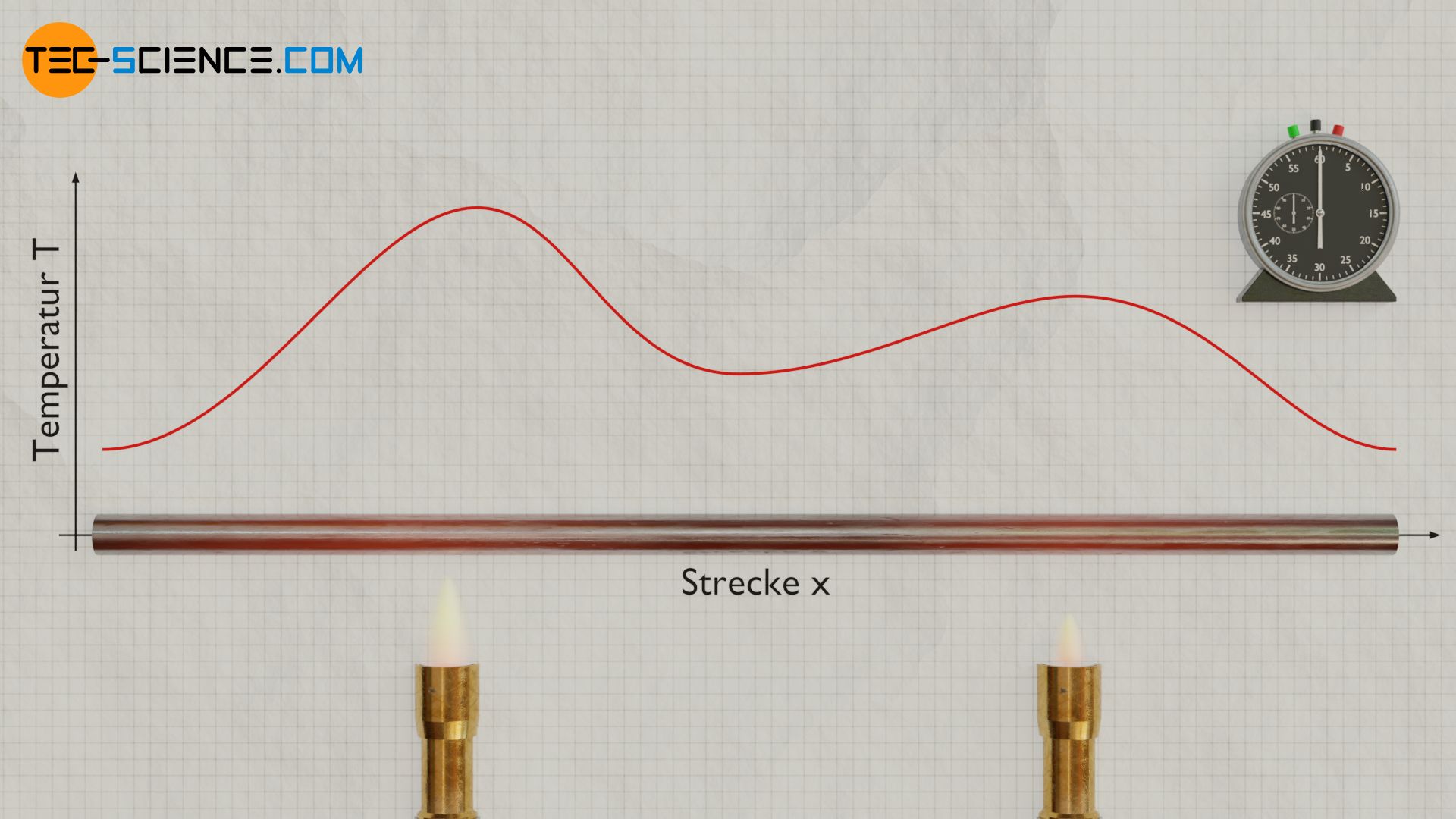
Die untere Abbildung zeigt zu einem bestimmten Zeitpunkt die Temperaturverteilung entlang eines Stabes. Des Weiteren ist der Temperaturgradient als erste Ableitung der Temperaturfunktion nach dem Ort eingezeichnet. Die örtliche Änderung dieses Temperaturgradienten entspricht der zweiten Ableitung der Temperatur und gemäß der Wärmeleitungsgleichung schließlich der zeitlichen Temperaturänderung. Man kann hieraus erkennen, dass im Bereich der Hochpunkte der Temperaturverteilung die zeitliche Temperaturänderung negativ ist und im Bereich der Tiefpunkte positiv. Dies bedeutet also, dass Bereiche mit hohen Temperaturen sich abkühlen und Bereiche mit niedrigen Temperaturen sich erwärmen. Es kommt folglich mit der Zeit zu einem Angleichen der Temperaturen, bis sich schließlich eine konstante Temperatur eingestellt hat.
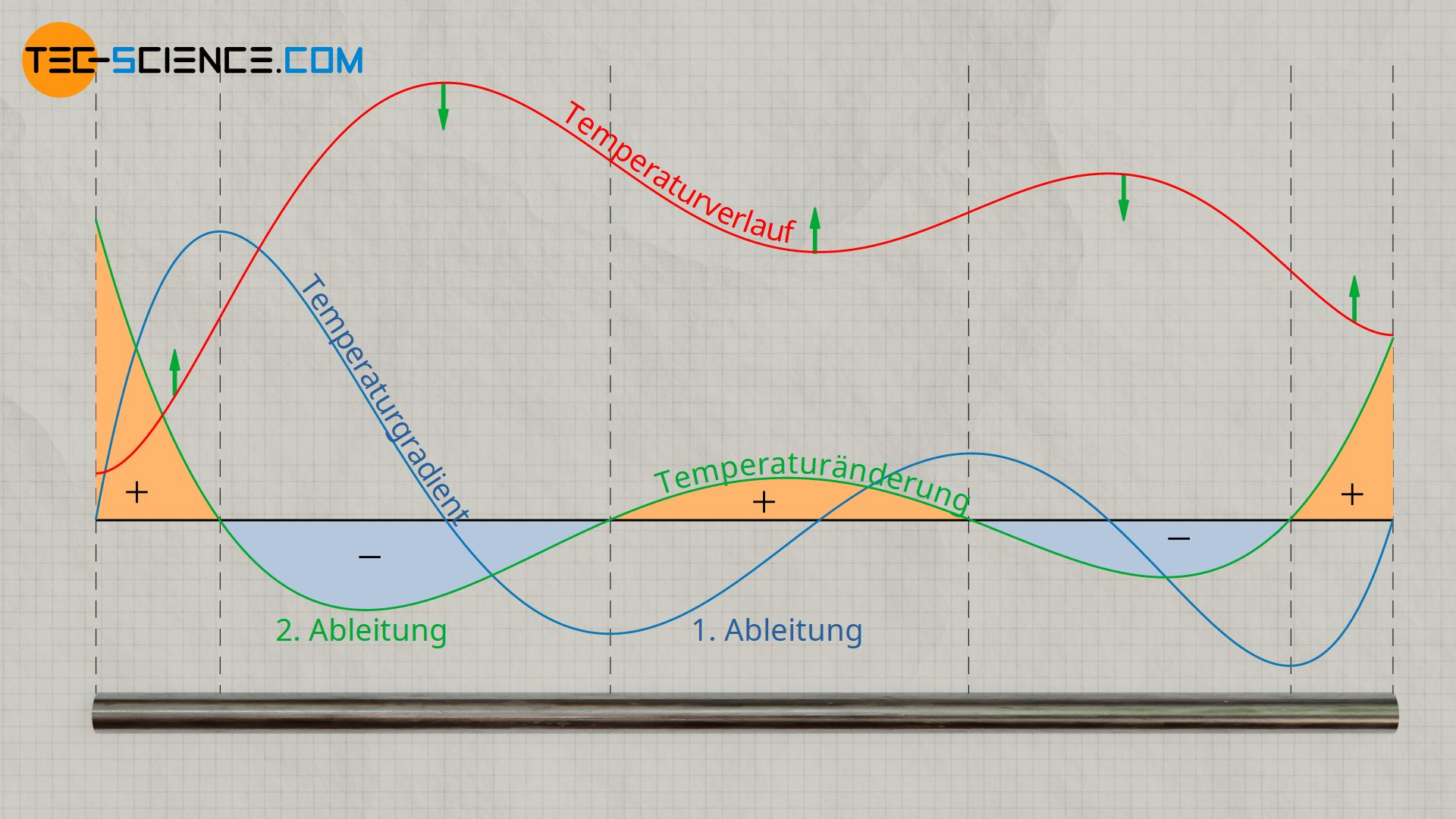
Temperaturleitfähigkeit
Im Folgenden soll der rein stoffabhängige Term λ/c⋅ϱ in der Wärmeleitungsgleichung näher interpretiert werden. Dieser stellt sozusagen den Proportionalitätsfaktor zwischen der örtlichen Änderung des Temperaturgradienten und der hieraus resultierenden zeitlichen Temperaturänderung dar. Dabei gilt offensichtlich, dass die zeitliche Temperaturänderung umso größer ist, …
- je größer die Wärmeleitfähigkeit ist und
- je geringer die spezifische Wärmekapazität ist und
- je geringer die Dichte des Materials ist.
Dass die Wärmeleitfähigkeit auf diese Weise Einfluss auf die Temperaturänderung hat, wird sehr schnell klar. Denn je größer die Wärmeleitfähigkeit, desto größer sind die Wärmeströme, die in einen Abschnitt ein- und austreten. Dies resultiert folglich auch in einem großen Netto-Wärmestrom, was wiederum eine starke zeitliche Änderung der Temperatur bedeutet.
Auch der Einfluss der Wärmekapazität des Materials auf die Temperaturänderung wird anschaulich klar, denn umso geringer die Wärmekapazität, desto weniger Wärme ist für eine gewünschte Temperaturänderung nötig. Umso geringer also die Wärmekapazität, desto stärker die Temperaturänderung bei gegebenem Netto-Wärmestrom.
Zudem wird auch anschaulich sehr schnell deutlich, dass die zeitliche Änderung der Temperatur von der Dichte des Materials abhängt. Je geringer nämlich die Dichte, desto weniger Masse hat ein betrachteter Streckenabschnitt. Und umso geringer die Masse, desto schneller wird sich ein Stoff bei gegebenem Wärmestrom erwärmen bzw. abkühlen. Somit wird auch anschaulich klar, dass eine geringere Dichte eine schnellere Temperaturerhöhung bedeutet.
Der Term λ/c⋅ϱ stellt also ein Maß dafür dar, wie schnell sich die Temperatur bei einer bestimmten Änderung des Temperaturgradienten ändert. Salopp formuliert bringt dieser Term zum Ausdruck, wie schnell sich die Temperaturen ausbreiten. Dieser Term wird deshalb auch als Temperaturleitfähigkeit a bezeichnet (auch Temperaturleitkoeffizient genannt):
\begin{align}
& \boxed{\frac{\partial T}{\partial t} = a \cdot \frac{\partial^2 T}{\partial x^2}} ~~~~~\text{mit}~~~ \boxed{a:=\frac{\lambda}{\rho \cdot c}} ~~~~~\text{Temperaturleitfähigkeit}\\[5px]
\end{align}
Ungeachtet dessen, dass sich Temperaturleitfähigkeit und Wärmeleitfähigkeit ineinander umrechnen lassen, gibt es in der Aussagekraft beider Größen dennoch Unterschiede. Während die Temperaturleitfähigkeit das instationäre Verhalten von Temperaturfeldern beschreibt, wird die Wärmeleitfähigkeit zur Berechnung von Wärmeströmen im stationären Zustand verwendet.
Diffusionsgleichung
Die prinzipielle Aussage der Wärmeleitungsgleichung ist, dass es bei Vorhandensein von unterschiedlichen Temperaturen zu entsprechenden Wärmeströmen kommt, die dann schließlich zu einem Temperaturausgleich führen. Die analoge Situation hat man auch bei Konzentrationsunterschieden in Stoffen. Aufgrund solcher Konzentrationsunterschiede entstehen Stoffströme, die zu einem Ausgleich der Konzentrationen führen. Deshalb ist es nicht verwunderlich, dass auch Diffusionsvorgänge mit formal derselben Gleichung beschrieben werden:
\begin{align}
& \boxed{\frac{\partial u}{\partial t} = k \cdot \frac{\partial^2 u}{\partial x^2}} \\[5px]
\end{align}
Folgende Größen können jeweils als analog zueinander betrachtet werden:
| Größe | Wärmeleitung (Wärmediffusion) | Stoffleitung (Stoffdiffusion) |
| u | Temperatur | Konzentration |
| k | Temperaturleitfähigkeit | Diffusionskoeffizient |
Anstelle von Temperaturunterschieden kann man sich also auch einfach Konzentrationsunterschiede denken (z.B. Tinte in einem mit Wasser gefüllten Behälter). Der Ausgleichsprozess verläuft in beiden Fällen nach denselben Gesetzmäßigkeiten. Umgekehrt kann man sich das Strömen der Wärme als eine Art Wärmediffusion gedacht vorstellen. Aus diesem Grund wird die Wärmeleitungsgleichung auch als Diffusionsgleichung bezeichnet.
Diffusionsgleichung für den dreidimensionalen Fall
Für den dreidimensionalen Fall einer Wärmeleitung müssen die Wärmeströme nicht mehr nur in eindimensionaler Richtung bilanziert werden, sondern in alle drei Richtungen (analog gilt dies natürlich auch für die Stoffströme im Falle der Diffusion). Man betrachtet in diesem Fall ein Volumenelement und bilanziert welche Wärmeströme jeweils in x-, y- und z-Richtung in das Volumenelement einströmen und auf der anderen Seite wieder ausströmen.
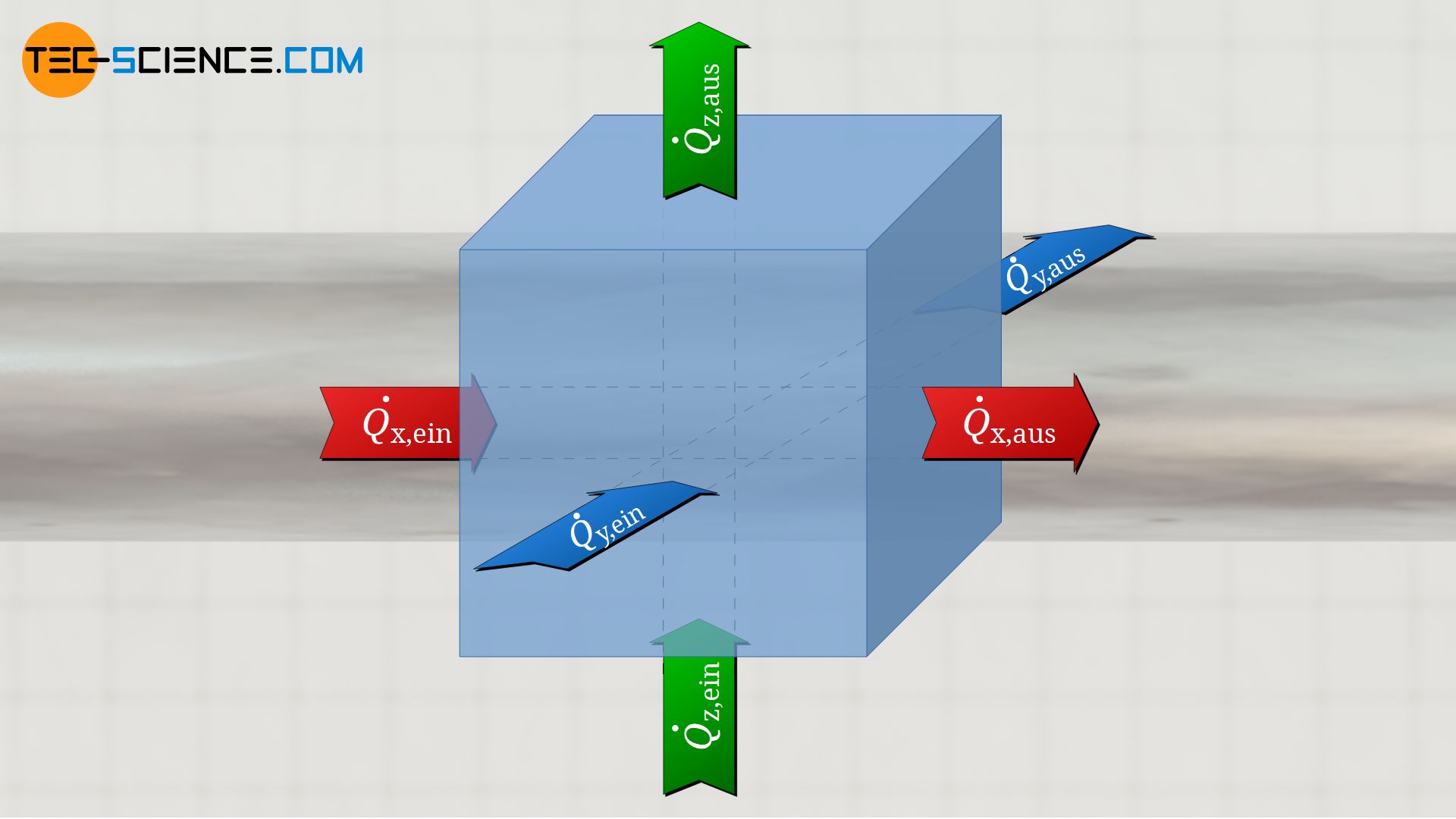
Die Summe aus diesen Einzelbilanzen ergibt der insgesamt auf das Volumenelement einströmende bzw. ausströmende Netto-Wärmestrom, welcher dann zur entsprechenden Änderung der Temperatur führt. Somit stellt sich die Diffusionsgleichung für den dreidimensionalen Fall wie folgt dar (isotropes Material vorausgesetzt, für das k in alle drei Raumrichtungen identisch ist):
\begin{align}
&\boxed{\frac{\partial u(\vec s,t)}{\partial t} = k \cdot \frac{\partial^2 u}{\partial x^2} + k \cdot \frac{\partial^2 u}{\partial y^2} + k \cdot \frac{\partial^2 u}{\partial z^2}} ~~~~~\text{mit: } ~~ \vec{s} = \left( \begin{array}{c} x \\ y \\ z \\ \end{array}\right) \\[5px]
\end{align}
Die Summe der zweifachen örtlichen Ableitungen in Richtung der jeweiligen Raumdimensionen wird mathematisch auch durch den sogenannten Laplace-Operator Δ ausgedrückt (Achtung: Der Laplace-Operator darf nicht mit dem Delta-Zeichen für Differenzen verwechselt werden!):
\begin{align}
&\boxed{\frac{\partial u(\vec s,t)}{\partial t} = k \cdot \Delta u(\vec s, t)} ~~~~~\text{mit}~~~\boxed{\Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}} \\[5px]
\end{align}
Die untere Simulation zeigt die Anwendung der Wärmeleitungsgleichung für den zweidimensionalen Fall. Es wird das Temperaturverhalten einer Platte simuliert, die an zwei Stellen erhitzt wird. Die Temperatur am Rand der Platte wurde als zeitlich konstant modelliert.
Wärmeleitungsgleichung mit innerer Wärmefreisetzung
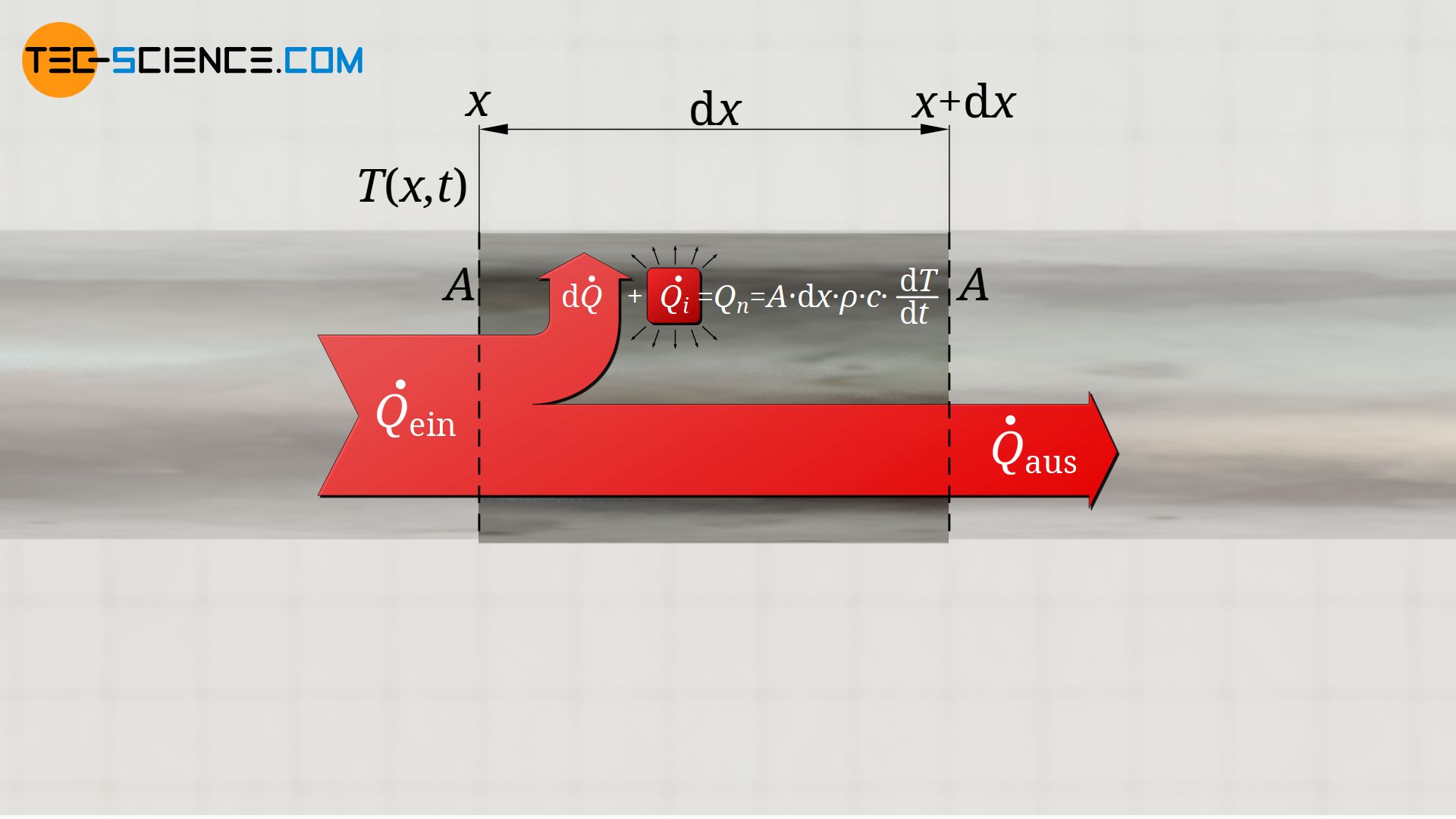
Bei der Herleitung der Wärmeleitungsgleichung wurde davon ausgegangen, dass der Netto-Wärmestrom eines betrachteten Streckenelement bzw. Volumenelements lediglich durch die Differenz in den zu- und abgeführten Wärmeströmen zustande kommt (aufgrund des Temperaturgradienten am Anfang und Ende des Abschnitts). Chemische Vorgänge im Inneren des Materials oder eine innere Wärmezufuhr können aber zusätzlich zu einem Wärmestrom führen. Dieser trägt dann ebenfalls zur Temperaturänderung bei. Unter Berücksichtigung eines solchen zusätzlichen Wärmestrom Q*i, ergibt sich Gleichung (\ref{kor}) dann wie folgt:
\begin{align}
&-\text{d}\dot Q + \dot Q_i= A \cdot \text{d}x \cdot \rho \cdot c \cdot \frac{\text{d}T}{\text{d}t} \\[5px]
\end{align}
Umstellen dieser Gleichung und einsetzen des Fourier’schen Gesetztes liefert folgenden Zusammenhang:
\begin{align}
& \frac{\text{d}T}{\text{d}t} =- \frac{1}{A \cdot \rho \cdot c} \cdot \frac{\text{d}\dot Q}{\text{d}x} + \frac{\dot Q_i}{A \cdot \text{d}x \cdot \rho \cdot c} \\[5px]
& \frac{\text{d}T}{\text{d}t} =\frac{\lambda}{\rho \cdot c} \cdot \frac{\text{d}^2 T}{\text{d}x^2} + \frac{\dot Q_i}{\underbrace{A \cdot \text{d}x }_{dV} \cdot \rho \cdot c } \\[5px]
& \frac{\text{d}T}{\text{d}t} =\frac{\lambda}{\rho \cdot c} \cdot \frac{\text{d}^2 T}{\text{d}x^2} +\frac{1}{\rho \cdot c} \cdot \underbrace{\frac{\dot Q_i}{dV}}_{\dot q_i} \\[5px]
& \frac{\text{d}T}{\text{d}t} =\frac{\lambda}{\rho \cdot c} \cdot \frac{\text{d}^2 T}{\text{d}x^2} +\frac{1}{\rho \cdot c} \cdot \dot q_i \\[5px]
\end{align}
Die Größe q*i beschreibt die zu einem bestimmten Zeitpunkt t an einer Stelle x im Inneren des Materials freigesetzte Wärmeenergie pro Zeiteinheit und pro Volumeneinheit. Für eine mathematisch korrekte Schreibweise lautet die eindimensionale Wärmeleitungsgleichung mit innerer Wärmefreisetzung somit wie folgt:
\begin{align}
&\boxed{\frac{\partial T(x,t)}{\partial t} = \frac{\lambda}{\rho \cdot c} \cdot \frac{\partial^2 T(x, t)}{\partial x^2} + \frac{1}{\rho \cdot c} \cdot \dot q_i(x,t) } \\[5px]
\end{align}
Für den dreidimensionalen Fall gilt entsprechend:
\begin{align}
&\boxed{\frac{\partial T(\vec s,t)}{\partial t} = \frac{\lambda}{\rho \cdot c} \cdot \Delta T(\vec s, t) + \frac{1}{\rho \cdot c} \cdot \dot q_i(\vec s,t) } \\[5px]
\end{align}