Die Prandtl-Zahl ist eine dimensionslose Ähnlichkeitskenngröße zur Beschreibung des Wärme- und Impulstransports.
Definition
Im Artikel zu den verschiedenen Grenzschichten wurde auf die Bedeutung dieser Grenzschichten was den Wärme- und Stoffübergang angeht, bereits ausführlicher eingegangen. Vor allem der Impulstransport innerhalb der hydrodynamischen Grenzschicht beeinflusst dabei den Wärmetransport in der thermischen Grenzschicht. Beide Transportvorgänge sind somit von entscheidender Bedeutung für den gesamten Wärmeübergang zwischen Wand und Fluid.
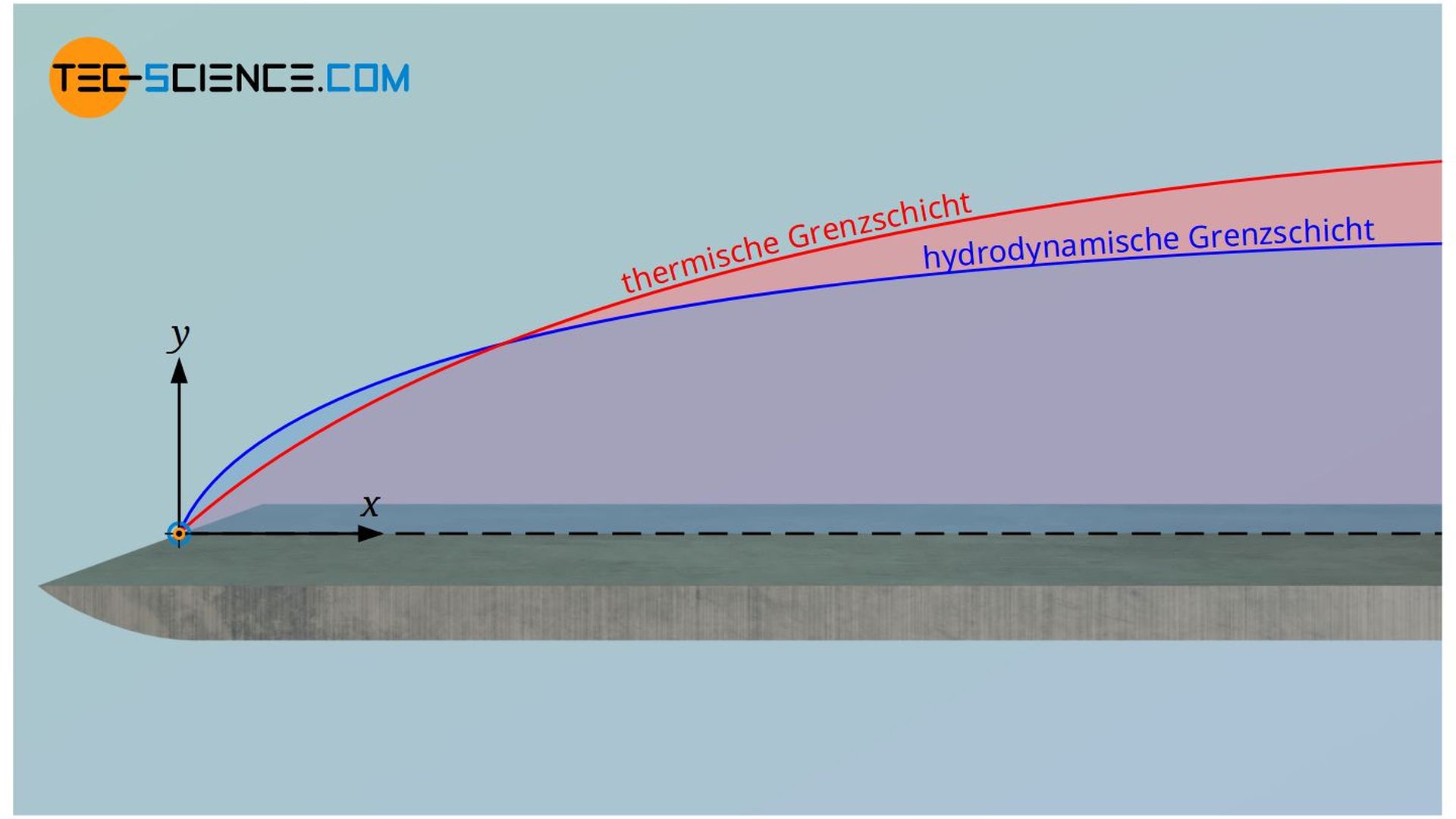
Das Verhältnis der Dicke zwischen Geschwindigkeitsgrenzschicht und Temperaturgrenzschicht spiegelt sich in der sogenannten Prandtl-Zahl wider. Die dimensionslose Prandtl-Zahl Pr ist definiert als das Verhältnis von Impulstransport (ausgedrückt durch die kinematische Viskosität ν) und Energietransport durch Wärmeleitung (ausgedrückt durch die Temperaturleitfähigkeit a):
\begin{align}
&\text{Prandtl-Zahl} = \frac{\text{Impulstransport}}{\text{Energietransport}} \\[5px]
\label{pr}
&\boxed{Pr = \frac{\nu}{a}} \\[5px]
\end{align}
Die kinematische Viskosität ν kann auch durch den Quotienten aus dynamischer Viskosität η und Dichte ϱ des Fluids ausgedrückt werden (ν=η/ϱ). Die Temperaturleitfähigkeit a wiederum kann durch die Wärmeleitfähigkeit λ, die Dichte ϱ und durch die spezifische Wärmekapazität cp ausgedrückt werden [a=λ/(cp⋅ϱ)]. Die Prandtl-Zahl lässt sich somit auch wie folgt ermitteln:
\begin{align}
\require{cancel}
&Pr = \frac{\nu}{a} =\frac{\eta \cdot c_p \bcancel{\rho}}{\bcancel{\rho} \cdot \lambda} \\[5px]
&\boxed{Pr = \frac{\eta \cdot c_p}{\lambda}} \\[5px]
\end{align}
Bei Prandtl-Zahlen größer 1 dominiert der Impulstransport gegenüber der Wärmeleitung. Die Geschwindigkeitsgrenzschicht ist in diesem Fall größer als die thermische Grenzschicht. Für gasförmiges Wasser mit einer relativ geringen Temperaturleitfähigkeit sind beide Grenzschichten ungefähr gleich groß. In diesem Fall liegt die Prandtl-Zahl in der Größenordnung von etwa 1.
Da die in den Formeln enthaltenen Größen im Allgemeinen von der Temperatur und dem Druck abhängen, wird die Prandtl-Zahl sowohl von der Temperatur als auch vom Druck beeinflusst. Bei Gasen ist die Temperaturabhängigkeit hingegen weniger stark ausgeprägt und kann meist als unabhängig der Temperatur angesehen werden.
Bedeutung der Prandtl-Zahl für die technische Praxis
Man kann an dieser Stelle bereits die praktische Bedeutung der Prandtl-Zahl erkennen. Untersucht man nämlich in einem Labor im verkleinerten Maßstab Wärmetransportvorgänge an strömenden Medien, so lassen sich die daran gewonnenen Erkenntnisse nur dann auf den realen Maßstab anwenden, wenn die Prandtl-Zahl identisch ist. Damit ist sichergestellt, dass Impulstransport und Energietransport im selben Maße ablaufen. Man kann in diesem Fall also auch von ähnlichen Voraussetzungen für den Wärmetransport ausgehen.
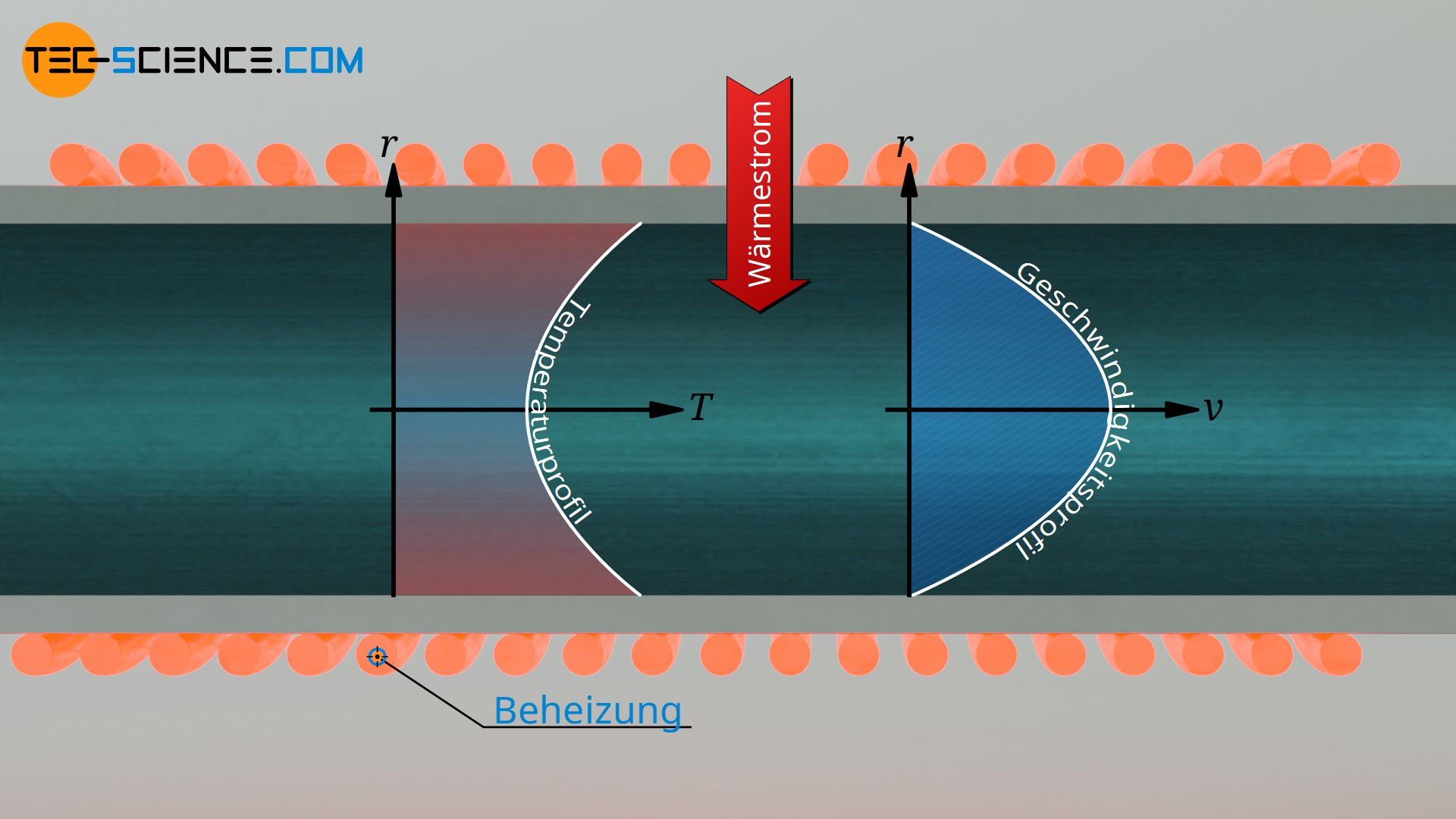
Man kann sich hierzu auch ein beheiztes Rohr vorstellen, das Wärme auf ein durchströmendes Fluid überträgt. Salopp formuliert beschreibt die Prandtl-Zahl in diesem Zusammenhang wie gut Wärme an der Rohrwand durch das Fluid geleitet wird und durch den Strömungsprozess abtransportiert wird. Dies ist entscheidend für den gesamten konvektiven Wärmeübergang. Deshalb hat die Prandtl-Zahl (neben der Reynolds-Zahl) besondere Bedeutung, wenn es um die Berechnung der Nusselt-Zahl geht, welche als weitere dimensionslose Kenngröße den konvektiven Wärmeübergang beschreibt.
Die Prandtl-Zahl ist eine dimensionslose Ähnlichkeitskenngröße zur Beschreibung des Wärme- und Impulstransports. Nur bei identischen Prandtl-Zahlen erhält man unabhängig der Größe des Systems stets physikalisch ähnliche Wärme- und Impulsströme.
Aufgrund der sehr guten Wärmeleitfähigkeit ist bei Strömungsvorgängen von flüssigen Metallen die thermische Grenzschicht meist deutlich ausgeprägter im Vergleich zur hydrodynamischen Grenzschicht. Die Wärme dringt sozusagen sehr stark in die Strömung vor und führt deshalb zu einer relativ großen thermischen Grenzschicht im Vergleich zur Geschwindigkeitsgrenzschicht. Die Prandtl-Zahl geht für flüssige Metalle deshalb gegen null. Quecksilber weist bei Raumtemperatur bspw. nur eine Prandtl-Zahl von 0,023 auf.
Bei Ölen mit erhöhter Viskosität ist die hydrodynamische Grenzschicht hingegen deutlich ausgeprägter als die Temperaturgrenzschicht. Die relativ geringe Temperaturleitfähigkeit führt dazu, dass Wärme nicht so stark in die Strömung vordringt. Gleichzeitig beeinflusst die hohe Viskosität des Öls die Strömung in einem weiten Bereich, d.h. es kommt zu einer relativ großen hydrodynamischen Grenzschicht. Die Prandtl-Zahlen sind in diesen Fällen deutlich größer als 1. So weist bspw. das bei Raumtemperatur hochviskose Glycerin eine Prandtl-Zahl von über 11.000 auf. Die Prandtl-Zahl sinkt allerdings mit zunehmender Temperatur aufgrund der damit verbundenen Abnahme der Viskosität.
Péclet-Zahl
Häufig hat man es in der Praxis mit Rohrströmungen zu tun, die zum Kühlen werden oder Heizen genutzt werden. Ziel dabei ist es, dass möglichst viel Wärme von der Wand an das Fluid (bzw. umgekehrt) übertragen wird. In diesem Zusammenhang stellt sich die Frage, ob große oder kleine Prandtl-Zahlen von Vorteil sind.
Betrachten wir hierzu eine Strömung in einem Rohr, das von außen erwärmt wird. Einen hohen Wärmestrom zwischen Wand und Fluid erhält man gemäß des Fourier’schen Gesetzes der Wärmeleitung immer dann, wenn der Temperaturgradient an der Wand sehr hoch ist.
Fluide die in diesem Zusammenhang eine hohe Temperaturleitfähigkeit aufweisen, würden die Wärme allerdings rasch im Fluid verteilen. Dies wiederum würde dazu führen, dass das Fluid im Extremfall eine einheitliche Temperatur über den gesamten Rohrquerschnitt hinweg besitzt. Bei einer hohen Temperaturleitfähigkeit würde sich die Temperatur des Fluids also rasch der Temperatur des Rohres anpassen. Man hätte dann allerdings keinen Temperaturabfall an der Wand mehr und der Wärmestrom käme zwischen Wand und Rohr käme zum Erliegen.
Hohe Temperaturleitfähigkeiten führen also zu einem geringen Wärmeübergang. Umgekehrt bedeutet dies, dass geringe Temperaturleitfähigkeiten zu großen Wärmeströmen führen, da bei solchen Fluiden ein höherer Temperaturgradient an der Wand besteht. Gemäß Gleichung (\ref{pr}) bedeuten geringe Temperaturleitfähigkeitswerte folglich hohe Prandtl-Zahlen. Für hohe konvektive Wärmeübergänge sind also hohe Prandtl-Zahlen von Vorteil.
Der Temperaturgradient an der Wand ist für den Wärmeübergang also immer die entscheidende Größe. Dieser wird aber auch durch die Geschwindigkeit beeinflusst. Für Newtonsche Fluide bildet sich ein parabolisches Geschwindigkeitsprofil im Rohr aus (siehe Hagen-Poiseuille Strömung). Je höher die mittlere Strömungsgeschwindigkeit ist, desto schneller wird die in das Fluid vorgedrungene Wärme abtransportiert. Die Wärme staut sich an der Wand sozusagen weniger auf, was wiederum zu einem größeren Temperaturgradienten führt. Hohe Strömungsgeschwindigkeiten begünstigen also ebenfalls den konvektiven Wärmeübergang. Da die Strömungsgeschwindigkeit wiederum durch die Reynolds-Zahl ausgedrückt werden kann, gilt also:
Hohe Prandtl-Zahlen und hohe Reynolds-Zahlen begünstigen den konvektiven Wärmetransport!
Das Produkt von Prandtl-Zahl und Reynoldszahl stellt letztlich ein Maß für die Stärke des konvektiven Wärmeübergangs dar. Damit kann eine neue dimensionslose Größe definiert werden, die sogenannte Péclet-Zahl Pe:
\begin{align}
\require{cancel}
\label{pe}
&\boxed{Pe:= Pr \cdot Re }=\frac{\bcancel{\nu}}{a} \cdot \frac{v \cdot L}{\bcancel{\nu}} \\[5px]
&\boxed{Pe= \frac{v \cdot L}{a}} \\[5px]
\end{align}
Darin bezeichnet L die charakteristische Länge des Systems, z.B. den Durchmesser eines Rohres bei Rohrströmungen oder die Plattenlänge bei Strömungen über eine Platte. Die Péclet-Zahl ist eine dimensionslose Ähnlichkeitskenngröße, die das Transportverhältnis zwischen (Impuls-)Strömung und (Wärme-)Diffusion beschreibt. Wie bereits erläutert, beeinflusst die Péclet-Zahl maßgeblich den konvektiven Wärmetransport in Rohrströmungen (siehe Artikel Berechnung der Nusselt-Zahlen für Rohrströmungen).
Gebrauchsformel zur Berechnung der Prandtl-Zahl für Luft und Wasser
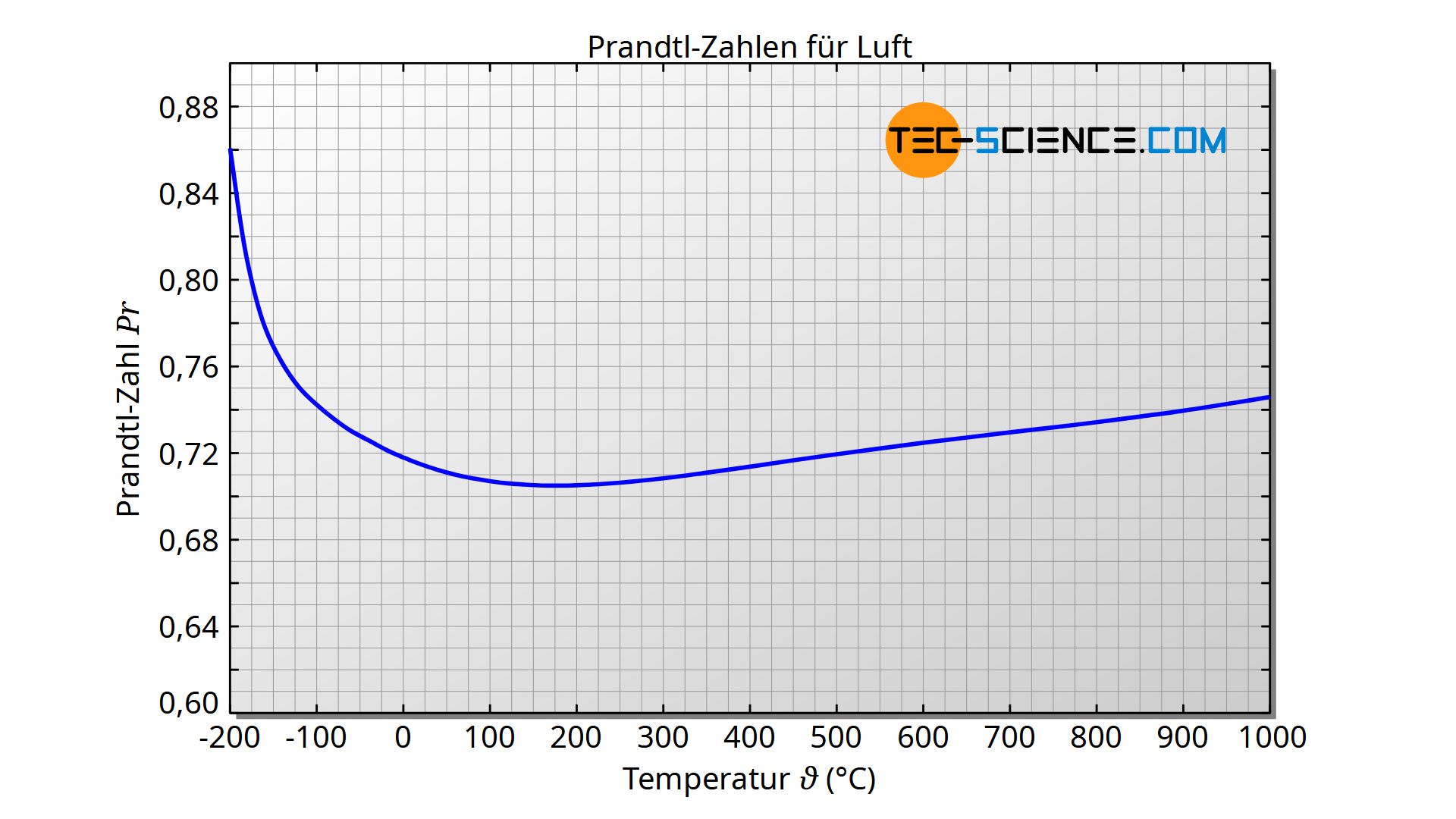
Luft liegt mit einer Prandtl-Zahl von 0,7 in einem Bereich, wo die hydrodynamische und die thermische Grenzschicht ungefähr gleich groß ist. Wie bereits erwähnt ist die Temperaturabhängigkeit dabei relativ gering. Bei einem Umgebungsdruck von 1 bar variiert die Prandtl-Zahl im Bereich zwischen -100 °C und +500 °C nur um maximal 5 %. Mit nachfolgend angegebener Formel kann die Prandtl-Zahl der Luft bei einem 1 bar im Temperaturbereich zwischen -100 °C und 500 °C mit einer Abweichung von maximal 0,1 % zum Literaturwert berechnet werden. Die Temperatur ist dabei in der Einheit „Grad Celsius“ einzusetzen.
\begin{align}
&\boxed{Pr_\text{Luft} = \frac{10^9}{1,1 \cdot \vartheta^3-1200 \cdot \vartheta^2 + 322000 \cdot \vartheta + 1,393 \cdot 10^9}}\\[5px]
&-100 °C <\vartheta < 500 °C \\[5px]
\end{align}
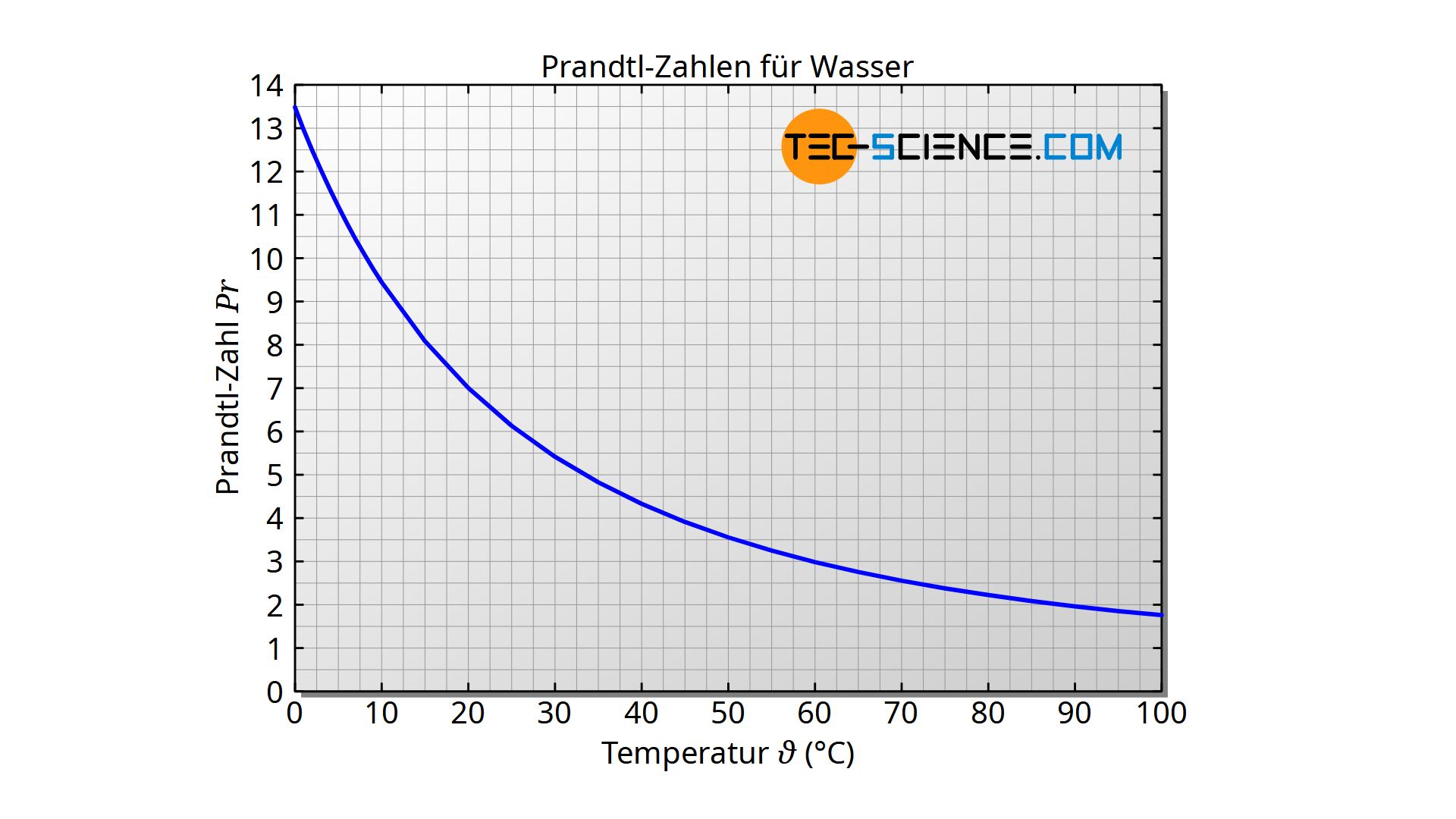
Im Falle von flüssigem Wasser reicht die Prandtl-Zahl bei einem Druck von 1 bar von 13,44 (bei 0 °C) bis zu 1,75 (bei 100 °C) Mit nachfolgend angegebener Formel kann die Prandtl-Zahl im Temperaturbereich zwischen 0 und 90 °C mit einer Abweichung von maximal 1 % zum Literaturwert ermittelt werden. Die Temperatur ist dabei in der Einheit „Grad Celsius“ einzusetzen.
\begin{align}
&\boxed{Pr_\text{Wasser} = \frac{50000}{\vartheta^2+155\cdot \vartheta + 3700}} ~~~0 °C <\vartheta < 90 °C\\[5px]
\end{align}