Neben der hydrodynamischen Grenzschicht beeinflusst auch die thermische Grenzschicht und die Konzentrationsgrenzschicht den gesamten Wärme- und Stofftransport einer Strömung entscheidend.
Temperaturgrenzschicht (thermische Grenzschicht)
Im Artikel zur hydrodynamischen Grenzschicht wurde am Beispiel einer überströmten Platte bereits ausführlich der Verlauf des Geschwindigkeitsprofils in laminaren und turbulenten Strömungen erläutert. Die Platte beeinflusst aber im Allgemeinen nicht nur die Strömungsgeschwindigkeit, sondern auch die Temperatur der Strömung, sofern sich die Temperatur des Fluids von der Platte unterscheidet. Betrachten wir deshalb mi folgenden eine isotherm beheizte Platte mit der Temperatur T0. Die Temperatur der ungestörten Anströmung betrage T∞.
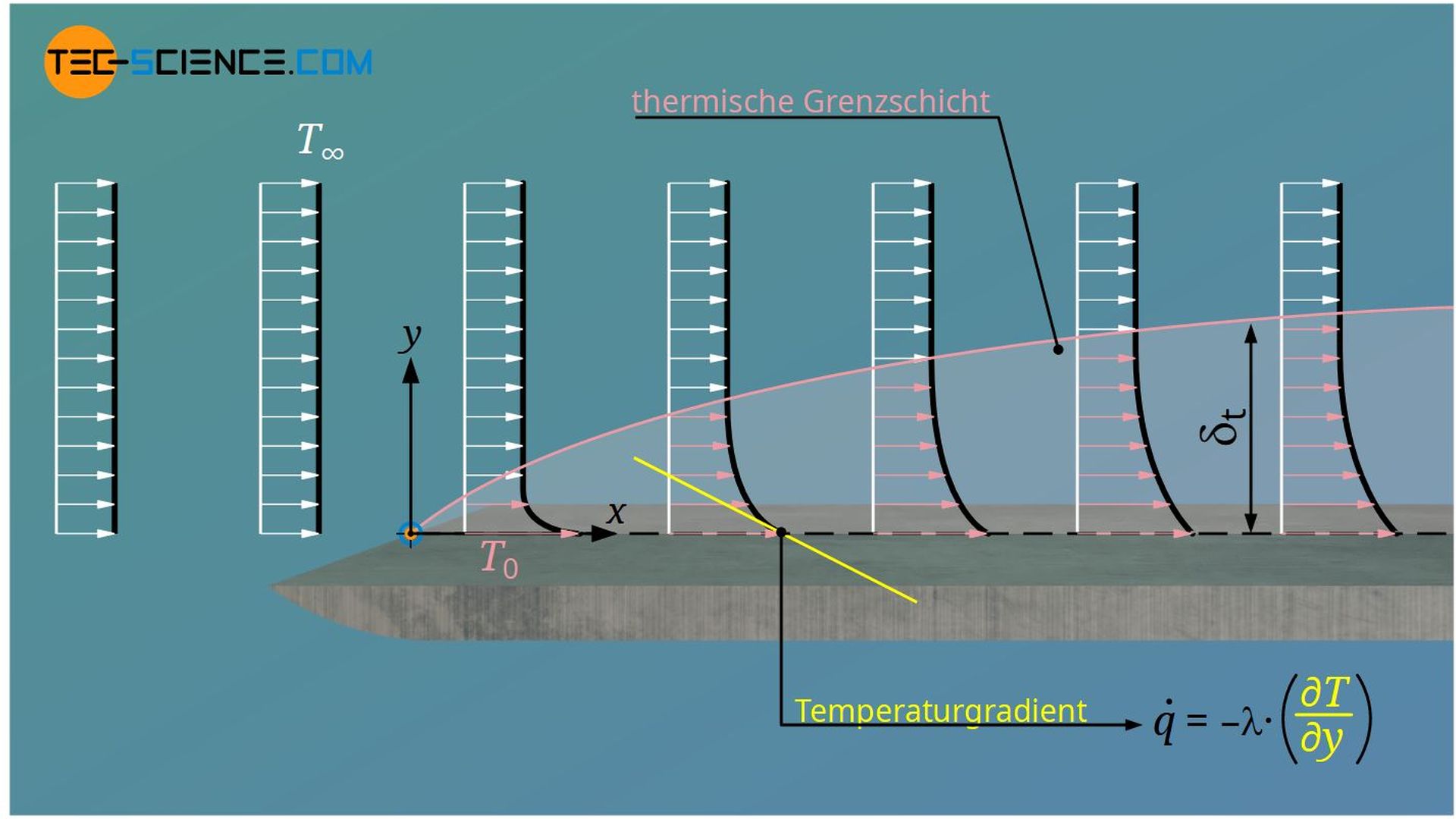
Die Temperatur des Fluids nimmt unmittelbar an der Wand die Temperatur der Platte T0 an, denn schließlich haftet das Fluid aufgrund der Haftbedingung dort. Die Temperatur nimmt senkrecht zur Hauptströmungsrichtung dann ab, bis in einem gewissen Abstand zur Wand die Temperatur T∞ der ungestörten Strömung erreicht ist. Analog zur Geschwindigkeitsgrenzschicht lässt sich somit eine Temperaturgrenzschicht definieren, die auch als thermische Grenzschicht bezeichnet wird.
Jener Randbereich bis wohin die Differenz zwischen lokaler Temperatur und Temperatur des ungestört strömenden Fluids 99% der Temperaturdifferenz zwischen Platte und ungestörter Strömung erreicht hat, wird auch als thermische Grenzschicht bezeichnet.
Auch die thermische Grenzschicht wächst wie die hydrodynamische Grenzschicht allmählich an, da die Wärme immer stärker in das Fluid vordringt und somit die Fluidschichten mit der Zeit erwärmt. Die thermische Grenzschicht ist also dadurch definiert, dass innerhalb deren Temperaturgradienten und somit auch Wärmetransportvorgänge existieren.
Der Wärmetransport hat gleichzeitig aber Auswirkungen auf den Strömungsprozess, da die Temperatur entscheidend die Viskosität des Fluids bestimmt. So beginnt das Fluid aufgrund der sinkenden Viskosität infolge einer Temperaturerhöhung bspw. plötzlich schneller zu strömen. Dies wiederum hat dann aber Auswirkungen auf den Abtransport der Wärme somit wieder auf die Strömung selbst. Die thermische und hydrodynamische Grenzschicht beeinflussen sich also gegenseitig. Die Dicke beider Grenzschichten unterscheiden sich im Allgemeinen voneinander!
Konzentrationsgrenzschicht (Stoffgrenzschicht)
Bei Mischungen von Fluiden wird ein Massetransport nicht nur durch Konvektionsströmungen hervorgerufen, sondern auch durch Konzentrationsunterschiede. Der damit verbundene Stofftransport durch Diffusion wird analog zum Wärmetransport durch Leitung beschrieben (siehe Artikel Ficksche Gesetze der Diffusion). Anstelle eines Wärmeleitkoeffizienten (Wärmeleitfähigkeit) und eines Temperaturgradienten, tritt im Falle des Stofftransports ein Diffusionskoeffizient D und ein Konzentrationsgradient ∂c/∂y. Die Wärmestromdichte \(\dot q\) entspricht bei der Diffusion einer Teilchenstromdichte \(\dot n\).
| Wärmetransport | Stofftransport | Impulstransport | |
|---|---|---|---|
| Gesetz von | Fourier | Fick | Newton |
| \begin{align} \notag &\boxed{\dot q = – \lambda ~\frac{\partial T}{\partial y}} \end{align} | \begin{align} \notag &\boxed{\dot n = – D~ \frac{\partial c}{\partial y}} \end{align} | \begin{align} \notag &\boxed{\tau = \eta~ \frac{\partial v}{\partial y}} \left(= \dot p_A\right) \end{align} | |
| Antrieb | Temperatur- gradient | Konzentrations- gradient | Geschwindigkeits- gradient |
| Charakteristische Größe | Wärmeleit- koeffizient | Diffusions- koeffizient | Viskosität |
| Stromdichte | Wärmestromdichte | Stoffstromdichte | Impulsstromdichte |
An dieser Stelle lässt sich auch gleich eine Analogie zum Impulstransport innerhalb der hydrodynamischen Grenzschicht ziehen. Tatsächlich hat die Schubspannung τ nämlich ebenfalls die Dimension einer Stromdichte (Analog zur Wärmestromdichte oder Teilchenstromdichte). So ist die Kraft definitionsgemäß nichts anderes als eine Impulsänderung pro Zeit (\(F=\frac{\Delta p}{\Delta t}=\dot p\)) und stellt somit ein Impulsstrom dar. Wird dieser Impulsstrom auf die Fläche bezogen, wie im Fall der Schubspannung \(\tau\), dann handelt es sich dabei letztlich um eine Impulsstromdichte (=\(\dot p_A\)).
Auch was die Gradienten angeht, zeigt sich eine Analogie zwischen allen drei Fällen. Der Antrieb für den Impulsstrom ist ein Geschwindigkeitsgradient, ganz analog wie ein Temperaturgradient der Antrieb eines Wärmestroms ist bzw. der Konzentrationsgradient der Antrieb für einen Stoffstrom darstellt. Analog zur thermischen Grenzschicht und zur Geschwindigkeitsgrenzschicht, lässt sich beim Stofftransport durch Diffusion eine Konzentrationsgrenzschicht definieren:
Jener Randbereich bis wohin die Differenz zwischen lokaler Konzentration und Konzentration des ungestört strömenden Fluids 99% der Konzentrationsdifferenz zwischen Platte und ungestörter Strömung erreicht hat, wird als Konzentrationsgrenzschicht bezeichnet.
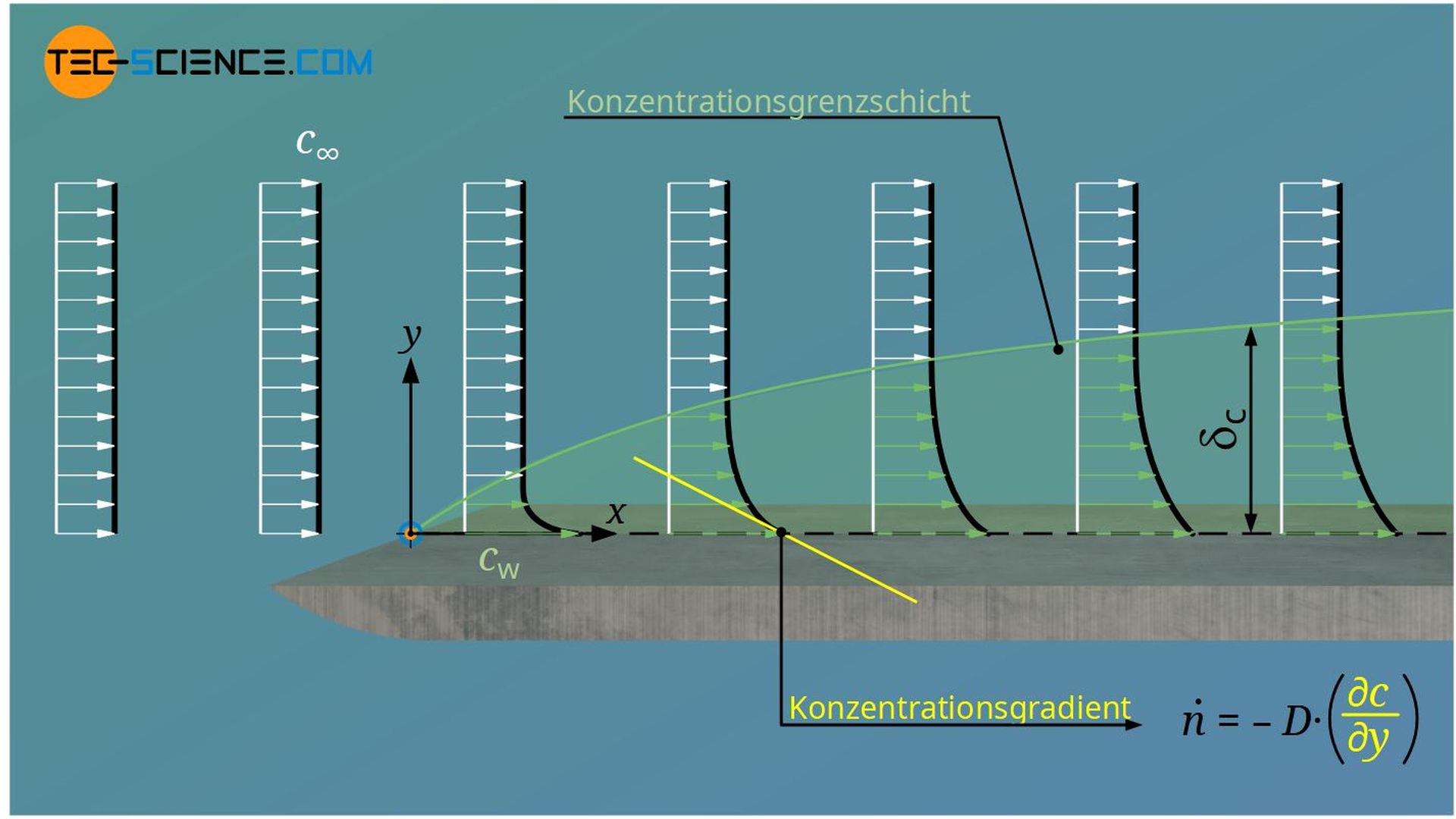
Auch dabei zeigt sich bei näherer Betrachtung, dass die Konzentrationsgrenzschicht nicht unabhängig von den Vorgängen in der Geschwindigkeitsgrenzschicht oder Temperaturgrenzschicht ist. Zum einen ist vor allem für Gase der Diffusionskoeffizient sehr stark von der Temperatur abhängig, sodass die thermische Grenzschicht unmittelbar Einfluss auf den Stofftransport nimmt. Zum anderen sorgen die konvektiven Strömungsvorgänge in der hydrodynamischen Grenzschicht dafür, dass die eindiffundierten Stoffteilchen abtransportiert werden. Erfolgt dieser Abtransport relativ rasch, dann bildet sich ein großer Konzentrationsgradient. Dieser wiederum hat einen verstärkten Stofftransport zur Folge. Somit beeinflusst also auch die Geschwindigkeitsgrenzschicht unmittelbar die Konzentrationsgrenzschicht.
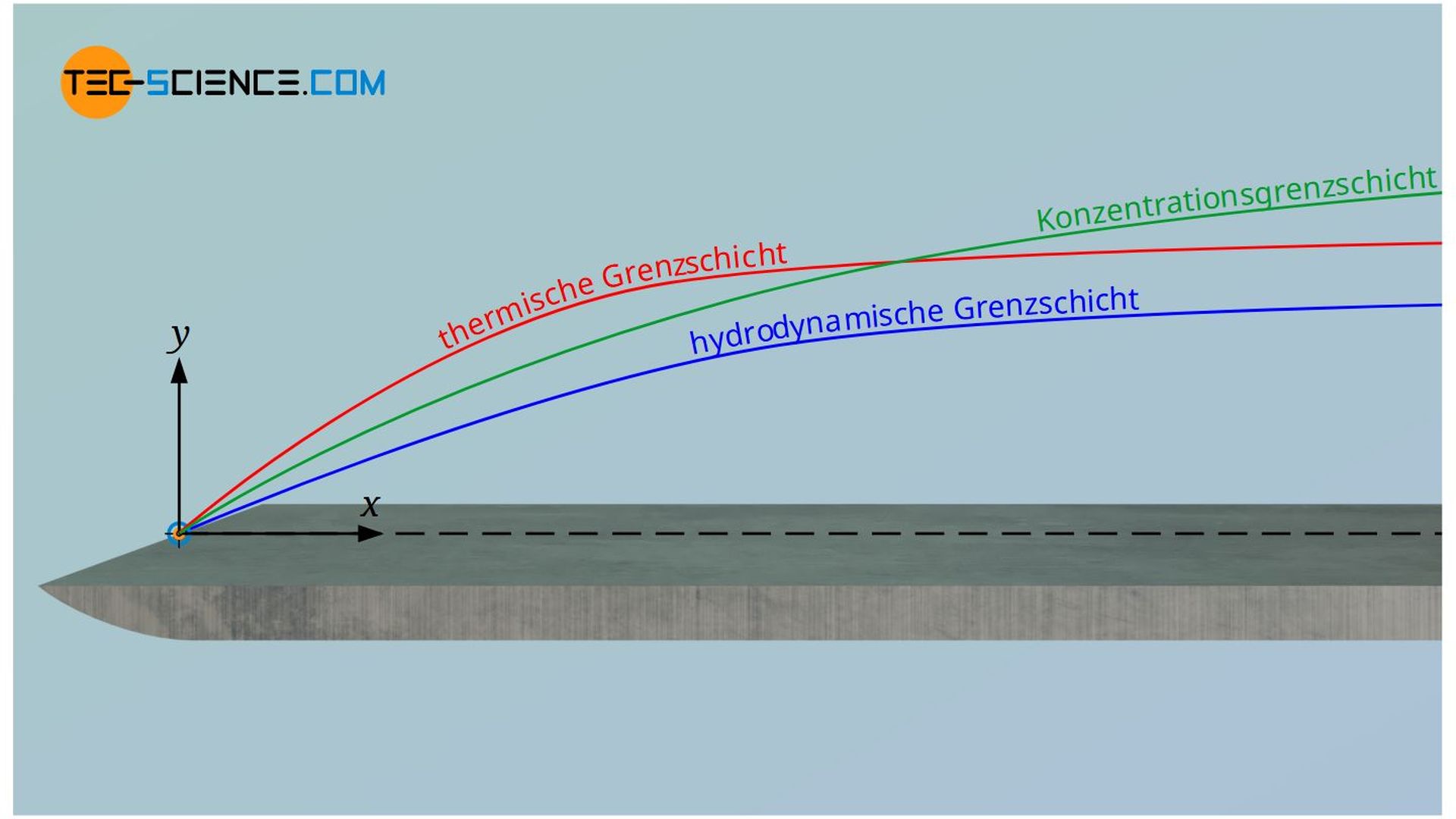
Als Fazit festzuhalten bleibt also, dass sich alle drei Grenzschichten stets gegenseitig beeinflussen und nicht unabhängig voneinander betrachtet werden können. Dies führt unmittelbar zu den dimensionslosen Kennzahlen, die jeweils zwei Grenzschichten miteinander ins Verhältnis setzen. Auf diese wird im Artikel näher eingegangen.






