Widerstandsbeiwert (Reibungsbeiwert und Druckbeiwert)

Widerstandsbeiwerte sind dimensionslose Ähnlichkeitskenngrößen zur Beschreibung des Widerstandes von umströmten Körpern.

Strömungswiderstand (Reibungswiderstand und Druckwiderstand)

Bewegt sich ein Körper durch ein Fluid oder wird ein Körper von einem Fluid umströmt, dann wirken auf den Körper Widerstandskräfte. Diese haben im Allgemeinen zwei Ursachen:

• Reibungskräfte (Schubspannungen)
• Druckkräfte (Normalspannungen)

Im Artikel Strömungswiderstand wurden diese beiden Mechanismen bereits ausführlich erläutert. Sie sollen an dieser Stelle nur nochmals kurz zusammengefasst werden.

Zum einen wirken aufgrund der Viskosität des Fluids Reibungskräfte auf den Körper, die zu einem gewissen Reibungswiderstand führen. Entscheidend sind dabei die wirkenden Schubspannungen an der Oberfläche des Körpers. Diese Schubspannungen werden auch als Wandschubspannungen τ_w bezeichnet.

Der Reibungswiderstand hat seine Ursache in den Wandschubspannungen, die aufgrund der Viskosität zwischen Fluid und Körperoberfläche wirken!

Zum anderen wirken auf den Körper im Allgemeinen unterschiedliche große statische Druckkräfte. Dies ist eine Folge der Energieerhaltung (siehe Bernoulli-Gleichung). Beschleunigt eine Strömung um einen Körper, dann sinkt der statische Druck, d.h. die Zunahme der kinetischen Energie geht zu Lasten der Druckenergie. Umgekehrt führt eine Abbremsung des Fluids zu einer Zunahme des statischen Drucks zu Lasten der kinetischen Energie. Die im Allgemeinen unterschiedlichen Drücke, die sich um den umströmten Körper ergeben, führen ebenfalls zu einer Widerstandskraft. Diese bezeichnet man auch als Druckwiderstand.

Der Druckwiderstand hat seine Ursache in den unterschiedlichen statischen Drücken, die aufgrund der Energieerhaltung am umströmten Körper wirken!

Beide Widerstandskräfte zusammen, d.h. Reibungswiderstand und Druckwiderstand, bilden dann den makroskopisch beobachtbaren Strömungswiderstand eines umströmten Körpers.

Die Summe aus Reibungswiderstand und Druckwiderstand entspricht dem Strömungswiderstand!

Reibungswiderstand, Druckwiderstand und Strömungswiderstand können jeweils mit dimensionslosen Kennzahlen beschrieben werden. Diese werden auch als Widerstandsbeiwerte oder kurz als Beiwerte bezeichnet. Die Bedeutung der dimensionslosen Beiwerte ist ganz analog zu anderen Ähnlichkeitskenngrößen wie bspw. Reynolds-Zahl, Prandtl-Zahl, Nusselt-Zahl, Schmidt-Zahl oder Lewis-Zahl (um nur ein paar zu nennen).

Die Widerstandsbeiwerte dienen dem Zwecke, strömungstechnische Vorgänge unabhängig der Größe des betrachteten Systems zu beschreiben. Auf diese Weise können bspw. die an einem Automodell im Windkanal gewonnen Erkenntnisse über die Widerstandskräfte auf das reale Fahrzeug übertragen werden.

Reibungsbeiwert

Zur dimensionslosen Charakterisierung des Reibungswiderstandes nutzt man den sogenannten Reibungsbeiwert. Der Reibungsbeiwert c_f setzt den Betrag der Wandschubspannung τ_w ins Verhältnis zur Strömungsgeschwindigkeit der Außenströmung v_∞. Die Strömungsgeschwindigkeit wird dabei in Form des dynamischen Drucks p_dyn,∞ der ungestörten Anströmung ausgedrückt. Beachte, dass beide Größen dieselbe Einheit haben und der Quotient somit dimensionslos ist. Der Reibungsbeiwert lässt sich damit als dimensionslose Wandschubspannung interpretieren.

\begin{align}
\label{cf}
&\boxed{c_f := \frac{\tau_w}{p_{\text{dyn},\infty}}}= \frac{\tau_w}{\tfrac{1}{2}\rho \cdot v_\infty^2} ~~~~~\text{(lokaler) Reibungsbeiwert}\\[5px]
\end{align}

Darin bezeichnet ϱ die Dichte des Fluids. Zieht man die Wurzel aus dem Quotienten von Schubspannung und Dichte, dann hat diese ebenfalls die Dimension einer Geschwindigkeit. Diese Größe wird auch als Schubspannungsgeschwindigkeit v_τ oder Reibungsgeschwindigkeit bezeichnet:

\begin{align}
\label{vw}
&\boxed{v_\tau := \sqrt{\frac{\tau_W}{\rho}}} ~~~~~\text{Schubspannungsgeschwindigkeit}\\[5px]
\end{align}

Die Schubspannungsgeschwindigkeit ist im eigentlichen Sinne keine Geschwindigkeit, sondern sie wird lediglich so genannt, weil diese Größe dieselbe Dimension wie eine Geschwindigkeit hat. Die Schubspannungsgeschwindigkeit beeinflusst nicht nur den Reibungsbeiwert, sondern auch die Dicke der viskosen Unterschicht.

Der Reibungsbeiwert kann also auch über das quadratische Verhältnis zwischen Schubspannungs- und Anströmgeschwindigkeit bestimmt werden:

\begin{align}
\label{cf2}
&\boxed{c_f = 2 \left(\frac{v_\tau}{v_\infty}\right)^2} \\[5px]
\end{align}

Im Falle einer ebenen Platte, ist mit dem Anwachsen der Grenzschicht eine Abnahme des Geschwindigkeitsgradienten an der Wand verbunden. Dies hat eine Abnahme der Wandschubspannung und somit eine Verringerung der Reibung zur Folge. Der Reibungsbeiwert ist also keineswegs eine konstante Größe, sondern hängt von den lokalen Bedingungen ab.

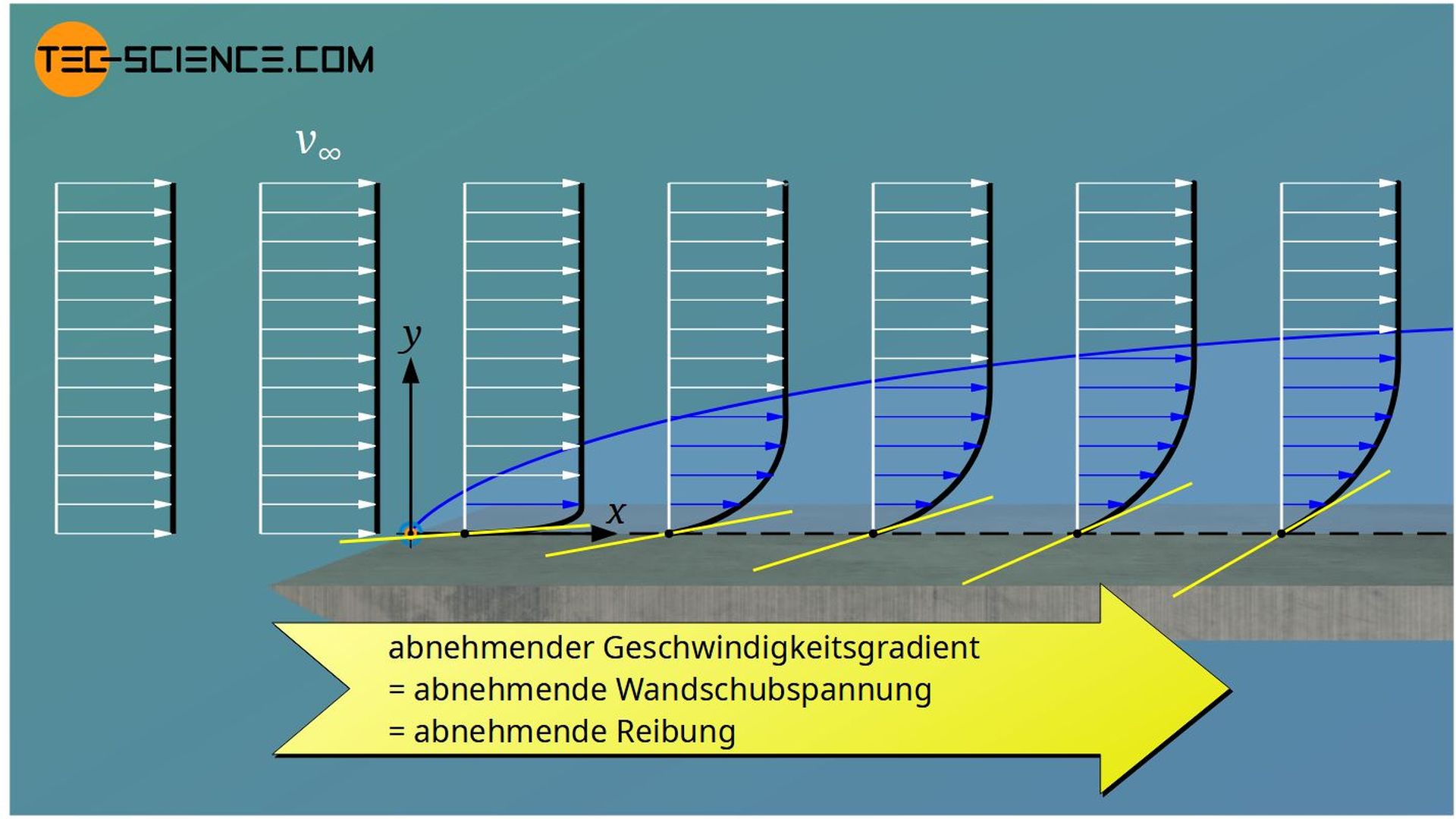
Laminare Umströmung einer Platte

Für eine ebene Platte und eine inkompressible laminare Strömung liefern die Grenzschichtgleichungen folgenden Zusammenhang zwischen der lokalen Reynoldszahl im Abstand x zur Plattenkante und dem dortigen Reibungsbeiwert c_f,lam (in der Formel bezeichnet ν die kinematische Viskosität des Fluids):

\begin{align}
&\boxed{c_\text{f,lam} = \frac{0,664}{\sqrt{Re_x}}} ~~~~~Re_x = \frac{v_\infty \cdot x}{\nu}~~~~~~~\text{(lokaler Reibungsbeiwert)}\\[5px]
\end{align}

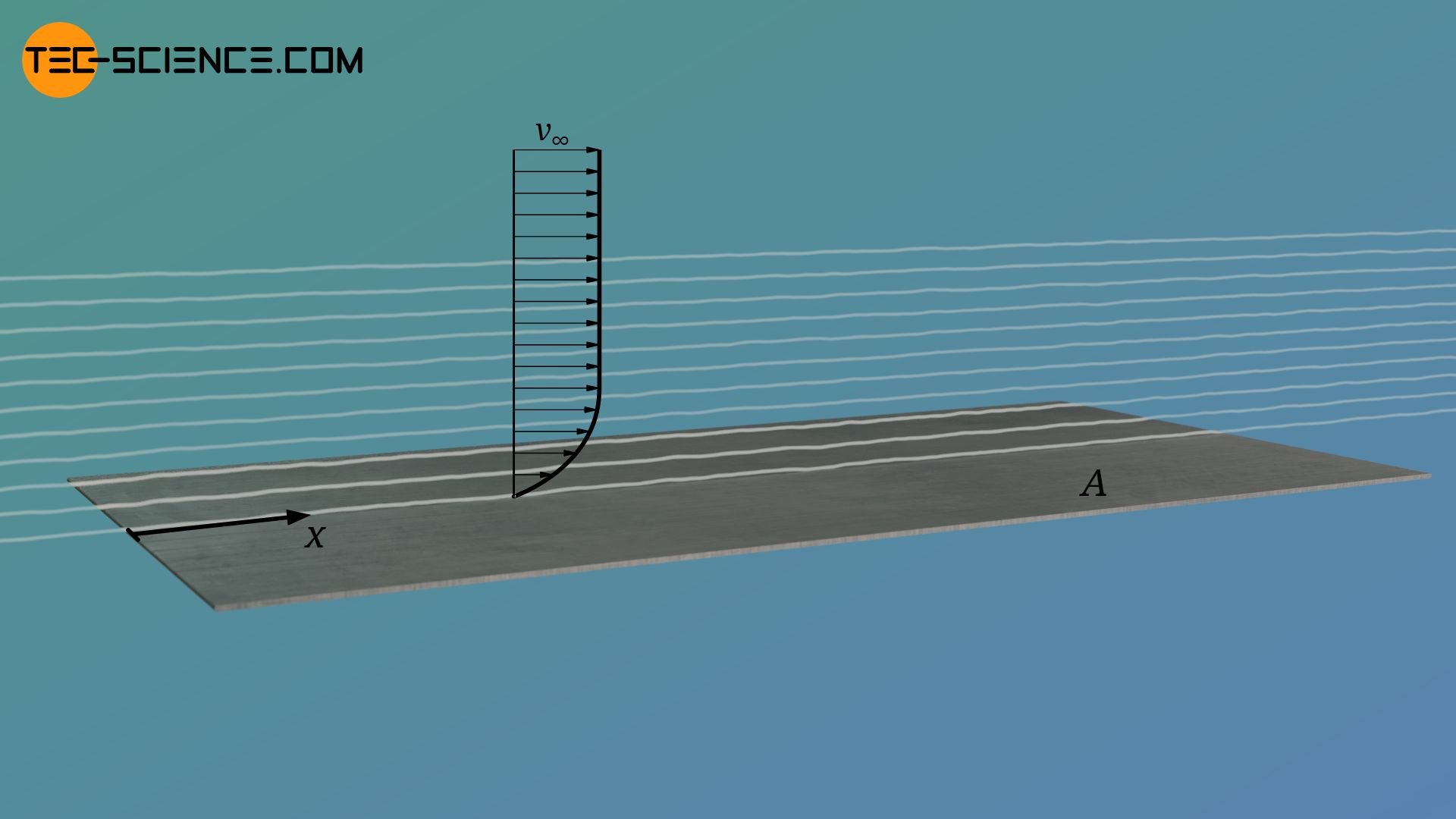
Durch Integration der lokalen Reibungsbeiwerte erhält man schließlich den gesamten Reibungsbeiwert C_f,lam der überströmten Plattenfläche. Die globale Reynolds-Zahl bezieht sich in diesem Fall auf die Gesamtlänge der Platte L.

\begin{align}
&\boxed{C_\text{f,lam} = \frac{1,328}{\sqrt{Re_L}}} ~~~~~Re_L = \frac{v_\infty \cdot L}{\nu} ~~~~~~~\text{(Gesamtreibungsbeiwert)}\\[5px]
\end{align}

Die Wandschubspannung in Gleichung (\ref{cf}) bezieht sich mit C_f,lam als Gesamtreibungsbeiwert dann auf die gesamte Plattenfläche A (mittlere Wandschubspannung τ_w). Für die angreifende Reibungskraft F_f,lam auf dieser Fläche gilt dann:

\begin{align}
& \overline{\tau}_w = \frac{F_\text{f,lam}}{A} = \frac{1}{2}\rho \cdot v_\infty^2 \cdot C_\text{f,lam} \\[5px]
&\boxed{F_\text{f,lam} = \frac{1}{2}\rho \cdot v_\infty^2 \cdot C_\text{f,lam} \cdot A} ~~\text{gilt für einseitig überströmte Platte}\\[5px]
\end{align}

Für eine beidseitig umströmte Platte ist die Reibungskraft offensichtlich doppelt so groß, da die Reibungskraft auf beiden Seiten wirksam ist:

\begin{align}
&\boxed{F_\text{f,lam} = \rho \cdot v_\infty^2 \cdot C_\text{f,lam} \cdot A} ~~\text{gilt für beidseitig umströmte Platte}\\[5px]
\end{align}

Turbulente Umströmung einer Platte

Im Artikel zu den Grenzschichten wurde gezeigt, dass sich die Dicke einer laminaren Grenzschicht umgekehrt proportional zur Wurzel der lokalen Reynoldszahl verhält:

\begin{align}
&\delta_\text{h,lam} \sim \frac{1}{\sqrt{Re_x}} \\[5px]
\end{align}

Dieser Einfluss zeigt sich nun direkt in den Reibungsbeiwerten für die laminare Strömung. Für eine turbulente Strömung ist der Zusammenhang allerdings folgender:

\begin{align}
&\delta_\text{h,tur} \sim \frac{1}{\sqrt[5]{Re_x}} \\[5px]
\end{align}

Es ist deshalb davon auszugehen, dass der Reibungsbeiwert einer turbulenten Strömung auf dieselbe Weise durch die lokale Reynolds-Zahl beeinflusst wird. Und tatsächlich gelten für die lokalen Reibungsbeiwerte bzw. den Gesamtreibungsbeiwert folgende Zusammenhänge:

\begin{align}
&\boxed{c_\text{f,tur} = \frac{0,0577}{\sqrt[5]{Re_x}}} ~~~~~Re_x = \frac{v_\infty \cdot x}{\nu}~~~~~~~\text{(lokaler Reibungsbeiwert)}\\[5px]
&\boxed{C_\text{f,tur} = \frac{0,0725}{\sqrt[5]{Re_L}}} ~~~~~Re_L = \frac{v_\infty \cdot L}{\nu} ~~~~~~~\text{(Gesamtreibungsbeiwert)}\\[5px]
\end{align}

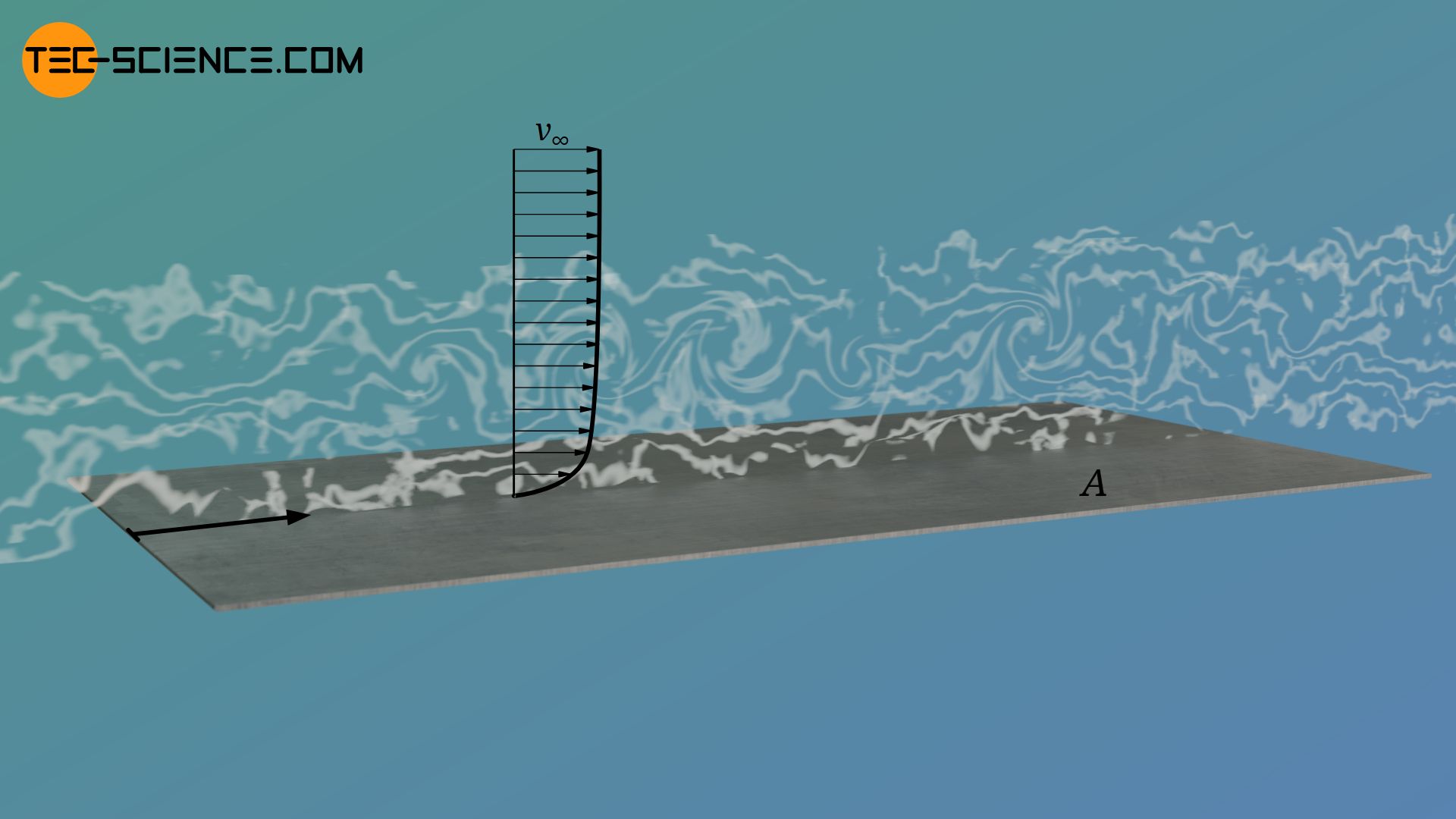
Für die Kraft auf eine turbulent überströmte bzw. umströmte Platte gilt somit:

\begin{align}
&\boxed{F_\text{f,tur} = \frac{1}{2}\rho \cdot v_\infty^2 \cdot C_\text{f,tur} \cdot A} ~~\text{gilt für einseitig überströmte Platte}\\[5px]
&\boxed{F_\text{f,tur} = \rho \cdot v_\infty^2 \cdot C_\text{f,tur} \cdot A} ~~\text{gilt für beidseitig umströmte Platte}\\[5px]
\end{align}

Druckbeiwert

Analog zum Reibungsbeiwert als dimensionslose Wandschubspannung, kann man einen Druckbeiwert als dimensionslose (statische) Druckdifferenz Δp_stat definieren.

\begin{align}
\label{cp}
&\boxed{c_p := \frac{\Delta p_\text{stat}}{p_{\text{dyn},\infty}}} = \frac{p_\text{stat}-p_{\text{stat},\infty}}{\tfrac{1}{2}\rho \cdot v_\infty^2}~~~~~\text{(lokaler) Druckbeiwert}\\[5px]
\end{align}

Darin bezeichnet p_stat den statischen Druck an jener Stelle an dem der Druckbeiwert bestimmt werden soll. p_stat,∞ ist der statische Druck in der ungestörten Anströmung und p_dyn,∞ der dynamische Druck der Anströmung. Beachte, dass die Druckdifferenz Δp_stat sozusagen der effektive wirksame Druck auf die umströmte Oberfläche ist.

Für stationäre, inkompressible und reibungsfreie Strömungen gilt gemäß der Energiegleichung nach Bernoulli folgender Zusammenhang zwischen einem Punkt in der ungestörten Anströmung und einem beliebigen Punkt am umströmten Körper:

\begin{align}
&p_{\text{stat},\infty}+\tfrac{1}{2}\rho \cdot v_\infty^2 = p_{\text{stat}}+\tfrac{1}{2}\rho \cdot v^2\\[5px]
\end{align}

Darin bezeichnet v_∞ die Strömungsgeschwindigkeit in der ungestörten Anströmung und v die Geschwindigkeit an einem beliebigen Punkt am reibungsfrei umströmten Körper. Umformen der oberen Gleichung und einsetzen in die Definition des Druckbeiwertes liefert für diese idealisierten Strömungen auch folgenden Zusammenhang zwischen den Strömungsgeschwindigkeiten und dem Druckbeiwert:

\begin{align}
&p_{\text{stat}} – p_{\text{stat},\infty} = \tfrac{1}{2}\rho \cdot v_\infty^2 – \tfrac{1}{2}\rho \cdot v^2 \\[5px]
\label{cpi}
&\boxed{c_p =1- \left(\frac{v}{v_\infty}\right)^2} ~~~\text{gilt für reibungsfreie und inkompressible Strömungen}\\[5px]
\end{align}

In einem Staupunkt wandelt sich die kinetische Energie der Strömung vollständig in statischen Druck um. Dort ergibt sich folglich die maximale (statische) Druckdifferenz zur Anströmung. Die Druckdifferenz entspricht gerade dem dynamischen Druck der ungestörten Strömung und der Druckbeiwert erreicht den maximalen Wert von 1. Dies sieht man auch direkt anhand von Gleichung (\ref{cpi}). Da die Strömung im Staupunkt bis zum Stillstand abgebremst wurde (v=0), folgt somit direkt c_p=1.

Der Druckbeiwert kann aber auch den Wert 0 annahmen. In diesem Fall ist der statische Druck an einer betrachteten Stelle genauso groß wie der statische Druck in der ungestörten Strömung. Somit existiert keine Druckdifferenz und der Druckbeiwert ist folglich null. Auch dies kann direkt anhand von Gleichung (\ref{cpi}) erkannt werden. Wird die Strömung nicht beschleunigt oder abgebremst, dann entspricht die lokale Strömungsgeschwindigkeit der Geschwindigkeit der ungestörten Anströmung und der c_p-Wert wird zu null.

Der Druckbeiwert kann allerdings auch negative Werte annehmen. Dies ist dann der Fall, wenn eine Strömung entlang eines Körpers beschleunigt (bspw. beim Überströmen von Luft über eine Tragfläche). Die Energie für das Beschleunigen bezieht die Strömung aus dem statischen Druck. Der lokale statische Druck ist dabei also geringer im Vergleich zur ungestörten Strömung. Die statische Druckdifferenz ist somit negativ, was zu negativen Werten für den Druckbeiwert führt (dies erklärt auch den Unterdruck über der Tragfläche und die damit verbundene Auftriebskraft). Auch dies zeigt Gleichung (\ref{cpi}) unmittelbar. Ist die lokale Geschwindigkeit größer als die der ungestörten Anströmung, dann ist der Geschwindigkeitsterm größer 1 und der c_p somit negativ.

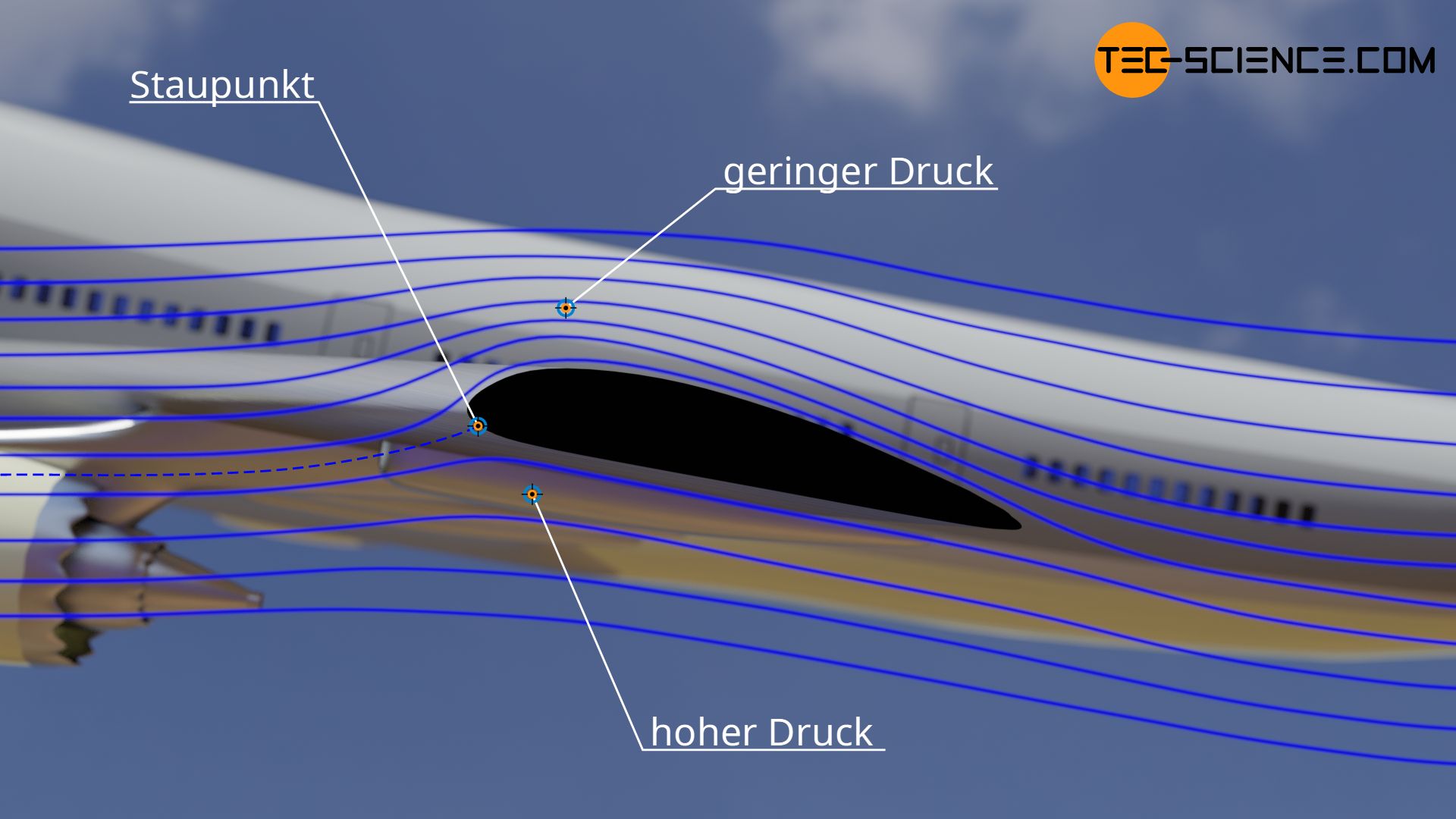
Man kann für inkompressible und reibungsfreie Strömungen also drei Fälle unterscheiden, die charakteristische Druckbeiwerte zur Folge haben:

Strömungsgeschwindigkeit …	nimmt zu	nimmt ab	bleibt konstant
Druckbeiwert	cp<0	0<cp<1	cp=0

Beachte, dass Druckbeiwerte zunächst nur die dimensionslose Druckverteilung um einen Körper beschreiben. Je nachdem wie die Oberfläche zur Strömung gerichtet ist, entstehen Kräfte in unterschiedliche Richtungen. Für den Druckwiderstand sind dabei nur diejenigen Kraftkomponenten entscheidend, die parallel zur Strömung gerichtet sind. Im Allgemeinen existieren auch Druckkräfte senkrecht dazu. Es sind genau diese Kräfte, die bspw. bei Tragflächen eine resultierende Kraft nach oben erzeugen und dem Flugzeug einen Auftrieb geben.

Strömungswiderstandsbeiwert

Wie bereits erläutert, ergeben die Summe aller in Strömungsrichtung wirkender Schubspannungskräfte und Druckkräfte über eine Oberfläche den Strömungswiderstand eines Körpers. Dies gilt entsprechend auch für die entdimensionierten Widerstandskräfte in Form der Widerstandsbeiwerte. Die Summe der beiden Widerstandsbeiwerte ergibt den Gesamtwiderstandsbeiwert c_w des Körpers.

\begin{align}
\label{ce}
&\boxed{c_w = c_f + c_p} ~~~~~\text{Gesamtwiderstandsbeiwert} \\[5px]
\end{align}

Der Gesamtwiderstandsbeiwert wird auch als Strömungswiderstandsbeiwert oder – etwas unpräzise – auch nur als Widerstandsbeiwert bezeichnet. Der genannte Zusammenhang der Beiwerte, lässt auch wie folgt herleiten. Sowohl die Wandschubspannung τ_w als auch der effektive wirksame Druck Δp_stat ergeben sich rein formal als Kraft pro Fläche, sodass für die entsprechenden Beiwerte gilt:

\begin{align}
&c_p = \frac{\Delta p_\text{stat}}{p_{\text{dyn},\infty}} = \frac{F_p}{\frac{1}{2}\rho \cdot v_\infty^2 \cdot A} \\[5px]
&c_f = \frac{\tau_w}{p_{\text{dyn},\infty}} = \frac{F_f}{\frac{1}{2}\rho \cdot v_\infty^2 \cdot A} \\[5px]
\end{align}

Die Summe aus Druckwiderstand F_p und Reibungswiderstand F_f ergibt schließlich den Gesamtwiderstand F_w:

\begin{align}
& F_p + F_f = F_w \\[5px]
\end{align}

Teilt man diese Gleichung durch den Ausdruck ½⋅ϱ⋅v_∞²⋅A, so ergibt sich auf der linken Seite gerade die Summe aus Druckbeiwert und Reibungsbeiwert. Die rechte Seite der Gleichung lässt sich als Gesamtwiderstandsbeiwert c_w interpretieren:

\begin{align}
& \underbrace{\frac{F_p}{\frac{1}{2}\rho \cdot v_\infty^2 \cdot A}}_{c_p} + \underbrace{\frac{F_f}{\frac{1}{2}\rho \cdot v_\infty^2 \cdot A}}_{c_f} = \underbrace{\frac{F_w}{\frac{1}{2}\rho \cdot v_\infty^2 \cdot A}}_{c_w} \\[5px]
\label{cw}
&\boxed{c_w:=\frac{F_w}{\frac{1}{2}\rho \cdot v_\infty^2 \cdot A}} \\[5px]
\end{align}

Wie bereits erläutert, ist bei stromlinienförmigen Körpern der Gesamtströmungsbeiwert hauptsächlich durch den Reibungsbeiwert bestimmt. Dabei kommt es nicht nur auf die Form an sich an, sondern auch auf den Anströmwinkel (Anstellwinkel). Bei nicht-stromlinienförigen Körpern (sog. stumpfe Körper), oder auch bei stromlinienförmigen Körpern mit großen Anstellwinkeln, beeinflusst der Druckbeiwert hingegen hauptsächlich den Gesamtströmungsbeiwert.

Experimentelle Bestimmung des Strömungswiderstandes

Mit Hilfe von numerischen Verfahren kann man den Druckbeiwert und den Reibungsbeiwert an den verschiedenen Stellen eines umströmten Körpers mathematisch ermitteln und zum Widerstandsbeiwert aufsummieren. In den meisten Fällen ist in der Praxis aber ohnehin der Widerstandsbeiwert als gesamtes relevant, da dieser schließlich den Strömungswiderstand eines Körper beschreibt. Dieser Strömungswiderstand kann man bspw. in Windkanälen relativ einfach ermitteln. Mann misst hierzu lediglich die von einer Strömung verursache Kraft auf einen umströmten Körper. Diese Widerstandskraft setzt man gemäß Gleichung (\ref{cw}) ins Verhältnis zur Fläche des umströmten Körpers.

Bei Zugrundelegung der Fläche ist jedoch Vorsicht geboten. Je nachdem welche Art der Widerstandskraft dominiert, kann sich die Fläche auf die in Strömungsrichtung projizierte Fläche beziehen oder auf die umströmte Fläche senkrecht zur Strömung. Bei Körpern wie bspw. Autos oder Motorräder beeinflusst entscheidend die senkrecht angeströmte Fläche den Strömungswiderstand, da der Druckwiderstand die maßgebende Größe ist (meist sogar noch verstärkt durch eine Strömungsablösung). Die projizierte Fläche entspricht anschaulich der Fläche des Schattens auf einer Wand, wenn man das Objekt in Strömungsrichtung beleuchtet.

Bei der Umströmung von Tragflächen hat die projizierte Fläche jedoch deutlich geringeren Einfluss, da der Reibungswiderstand dominiert. Dieser ist von der umströmten Fläche abhängig. Diese Fläche entspricht der Schattenfläche, wenn man die Tragfläche senkrecht zur Strömung von oben beleuchten würde.

Einfluss der Reynolds-Zahl auf den Widerstandsbeiwert

Der c_w-Wert ist keine reine Form-Konstante eines umströmten Körpers, sondern hängt im Allgemeinen von der Strömungsgeschwindigkeit v_∞, der (charakteristischen) Länge L des Körpers und von der kinematischen Viskosität ν des umströmten Fluids ab. Diese Größen werden durch die sogenannte Reynolds-Zahl Re verkörpert:

\begin{align}
&Re=\frac{v_\infty \cdot L}{\nu} \\[5px]
\end{align}

Der Widerstandsbeiwert ist im Allgemeinen also eine Funktion der Reynolds-Zahl:

\begin{align}
&c_w=c_w(Re) \\[5px]
\end{align}

Da die Reynolds-Zahl selbst von der Strömungsgeschwindigkeit abhängig ist, kann dies bei einigen Situationen dazu führen, dass der quadratische Einfluss der Strömungsgeschwindigkeit auf den Strömungswiderstand insgesamt verloren geht. Dies ist bspw. bei einer laminaren Strömung mit geringer Strömungsgeschwindigkeit der Fall, bei der sich die Strömung nicht vom umströmten Objekt löst (siehe auch Artikel Grenzschichtablösung). In diesem Fall sinkt der c_w-Wert nahezu umgekehrt proportional mit der Reynolds-Zahl, wobei die Widerstandskraft F_w formal mit dem Quadrat der Geschwindigkeit ansteigt. In diesem Fall ergibt sich dann eine lineare Abhängigkeit der Widerstandskraft von der Strömungsgeschwindigkeit:

\begin{align}
&F_w \sim \frac{1}{Re} \cdot v_\infty^2 \sim v_\infty \\[5px]
\end{align}

Dieser lineare Zusammenhang gilt in sehr guter Näherung für Reynolds-Zahlen kleiner 1, d.h. wenn die Zähigkeit des Fluids sehr viel größer als die Trägheit des Fluids ist. Dies setzt geringe Strömungsgeschwindigkeiten und geringe Körperabmessungen bei gleichzeitig hoher Viskosität des Fluids voraus. Für solche Fälle entwickelte der Mathematiker und Physiker George Stokes sein berühmtes Stoke’sches Reibungsgesetz für kugelförmige Körper.

In der Technik, wenn es um Luftströmungen um Autos oder Flugzeugen geht, sind die Reynolds-Zahlen im Allgemeinen wesentlich größer. In diesen Fällen ist der Einfluss der Reynolds-Zahl auf den Widerstandsbeiwert sehr gering und der Beiwert kann als nahezu konstant betrachtet werden. Dabei gilt dann wieder der quadratische Zusammenhang zwischen Geschwindigkeit und Widerstandskraft.

Zahlenbeispiel: Wie betrachten einen Körper, dessen Abmessung (charakteristische Länge) in der Größenordnung von einem Meter liegt. Dieser Gegenstand wird von Luft umströmt, wobei die Strömungsgeschwindigkeit in der Größenordnung von einem Meter pro Sekunde liegt. In diesem Fall erhält man bereits Reynolds-Zahlen, die in der Größenordnung von mehreren Zehntausend liegen! Würde man hingegen kleine Partikel in der Größenordnung von einigen Mikrometern in einer Wasserströmung mit einer Fließgeschwindigkeit von wenigen Zentimetern pro Sekunde betrachten, dann erhielte man Reynolds-Zahlen in der Größenordnung von 0,01.

Dieses Beispiel macht also deutlich, dass aufgrund der großen Reynolds-Zahlen in der Praxis sehr häufig von einem quadratischen Einfluss der Strömungsgeschwindigkeit auf die Widerstandskraft ausgegangen werden kann.

Bedeutung des quadratischen Einflusses der Geschwindigkeit auf den Strömungswiderstand

Wird ein Körper mit der Kraft F und der Geschwindigkeit v bewegt, dann setzt dieser Körper folgende mechanische Leistung P um:

\begin{align}
&P = F \cdot v \\[5px]
\end{align}

Bei motorisieren Fahrzeugen, wird diese Leistung vom Motor geliefert. Die Kraft des Motors entspricht dabei genau jener Kraft, die zur Kompensation des Strömungswiderstandes F_w erforderlich ist (Rollreibung und Gleitreibung ist bei hoher Geschwindigkeit vernachlässigbar). Zur Überwindung des Strömungswiderstandes muss der Motor also folgende Leistung aufwenden (Widerstandsleistung):

\begin{align}
&P_w = F_w \cdot v \\[5px]
\end{align}

Da die Widerstandskraft aber mit dem Quadrat der Geschwindigkeit anwächst, nimmt die Leistung insgesamt mit der dritten Potenz der Geschwindigkeit zu. Eine Verdopplung der Geschwindigkeit eines Fahrzeuges bedeutet also eine 8-fach so große Motorleistung! Dies hat bspw. enorme Auswirkungen auf den Treibstoffverbrauch, welcher direkt mit der Motorleistung in Zusammenhang steht. So würde bspw. die Reduktion der Geschwindigkeit von 140 km/h auf 110 km/h die benötigte Motorleistung zur Kompensation des Strömungswiderstandes um mehr als die Hälfte reduzieren!

Ganz allgemein gilt: Eine Verringerung der Geschwindigkeit um 20 % reduziert die Widerstandsleistung um etwa 50 %!

Typische Strömungsbeiwerte für ausgewählte Körperformen

Die untere Tabelle zeigt für ausgewählte Körper die typischen Strömungsbeiwerte. Mit Hilfe der charakteristischen Fläche des Körpers, kann dann der Strömungswiderstand bei gegebener Strömungsgeschwindigkeit und Dichte des Fluids wie folgt ermittelt werden:

\begin{align}
&\boxed{F_w=\frac{1}{2}\rho \cdot v_\infty^2 \cdot A \cdot c_w } \\[5px]
\end{align}

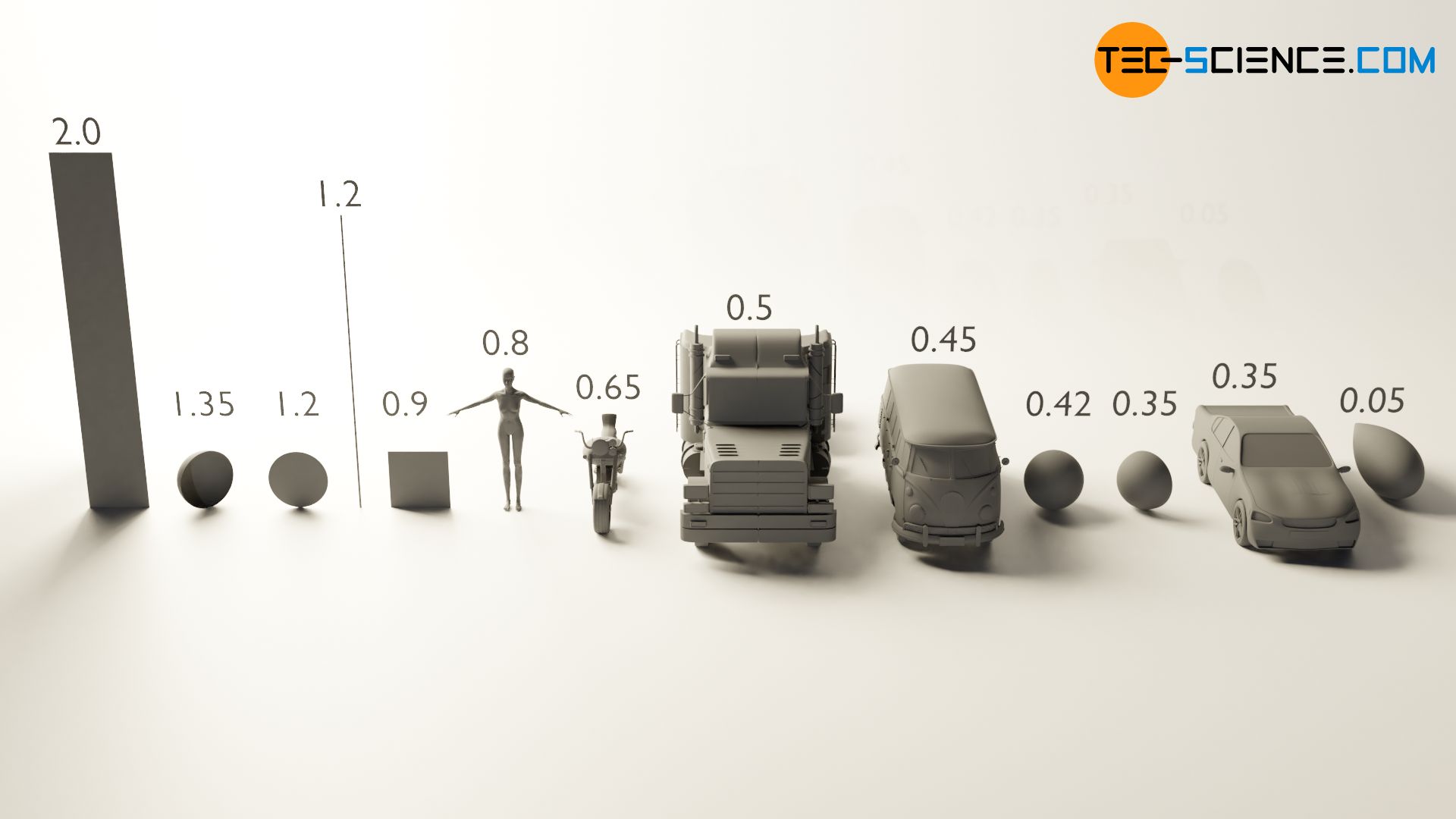
Bei bewegten Körpern durch ruhende Fluide (bspw. ein Auto oder ein Flugzeug durch Luft) entspricht die Strömungsgeschwindigkeit dann der Geschwindigkeit des sich bewegenden Körpers. Die Strömungsgeschwindigkeit entspricht also immer der Relativgeschwindigkeit zwischen Körper und Fluid. Im Falle von Luft als Fluid, spricht man in diesem Zusammenhang auch von der Luftwiderstandskraft oder kurz vom Luftwiderstand.

Körper	Widerstandsbeiwert (cw-Wert)
Motorrad	0,65
Auto	0,35
Bus	0,45
LKW	0,5
Mensch (stehend)	0,8
Kugel*	0,42 (für Re = 70.000)
Halbe Hohlkugel (konvexe Seite angeströmt)	0,35
Halbe Hohlkugel, „Fallschirm“ (konkave Seite angeströmt)	1,35
Tragfläche	0,1
Regentropfen (Stromlinienkörper)	0,05
Kreisscheibe	1,2
quadratische Platte	0,9
(unendlich) lange rechteckige Platte	2,0
langer dünner Draht	1,2

*) Für laminare Strömungen kann nach Kaskas folgende Näherungslösung zur Bestimmung des c_w-Wertes einer Kugel genutzt werden:

\begin{align}
&\boxed{c_w = \frac{24}{Re} +\frac{4}{\sqrt{Re}}+0,4}~~Re<2\cdot 10^5 \\[5px]
\end{align}

Beachte, dass für große Strömungsgeschwindigkeiten der Widerstandsbeiwert asymptotisch gegen 0,4 geht. Für sehr kleine Reynolds-Zahlen sind hingegen die letzten beiden Terme vernachlässigbar und es gilt das Gesetz von Stokes:

\begin{align}
&\boxed{c_w = \frac{24}{Re}}~~Re<1 \\[5px]
\end{align}

Dies führt zu der bereits angesprochenen Tatsache, dass die Widerstandskraft dann nicht mehr quadratisch mit der Geschwindigkeit ansteigt, sondern proportional.

Während bei einer Kugel die Strömungsrichtung offensichtlich keine Rolle spielt, ist sie bei einer Halbkugelschale allerdings von entscheidender Bedeutung. Trifft die Strömung auf die offene Seite der Halbkugel so ist der Widerstandsbeiwert fast vier mal so hoch im Vergleich zur Anströmung der kugelförmigen Seite. Die Kraft, die eine Strömung auf die Halbkugel mit der offenen Seite in Strömungsrichtung ausübt, ist entsprechend vier mal so groß. Dies macht man sich bspw. in sogenannten Schalenanemometern zu Nutze, um eine definierte Drehrichtung zu erzeugen. Die Drehzahl ist dabei ein Maß für die Windgeschwindigkeit.