Die Nusselt-Zahl ist eine dimensionslose Ähnlichkeitskenngröße zur Beschreibung des konvektiven Wärmeübergangs, unabhängig der Größe des Systems.
Einleitung
Der konvektive Wärmeübergang beschreibt den Wärmetransport zwischen einer festen Oberfläche und eines strömenden Fluids. Der dabei übertragene Wärmestrom ist umso höher, je größer die Temperaturdifferenz zwischen fester Wand und strömendem Fluid ist. Mit Hilfe eines sogenannten Wärmeübergangskoeffizienten α wird der Zusammenhang zwischen Temperaturdifferenz und Wärmestromdichte quantitativ beschrieben:
\begin{align}
\label{qq}
&\boxed{\dot q_\alpha = \alpha \cdot (T_W-\overline{T_F})} ~~~~~\text{konvektiver Wärmeübergang} \\[5px]
\end{align}
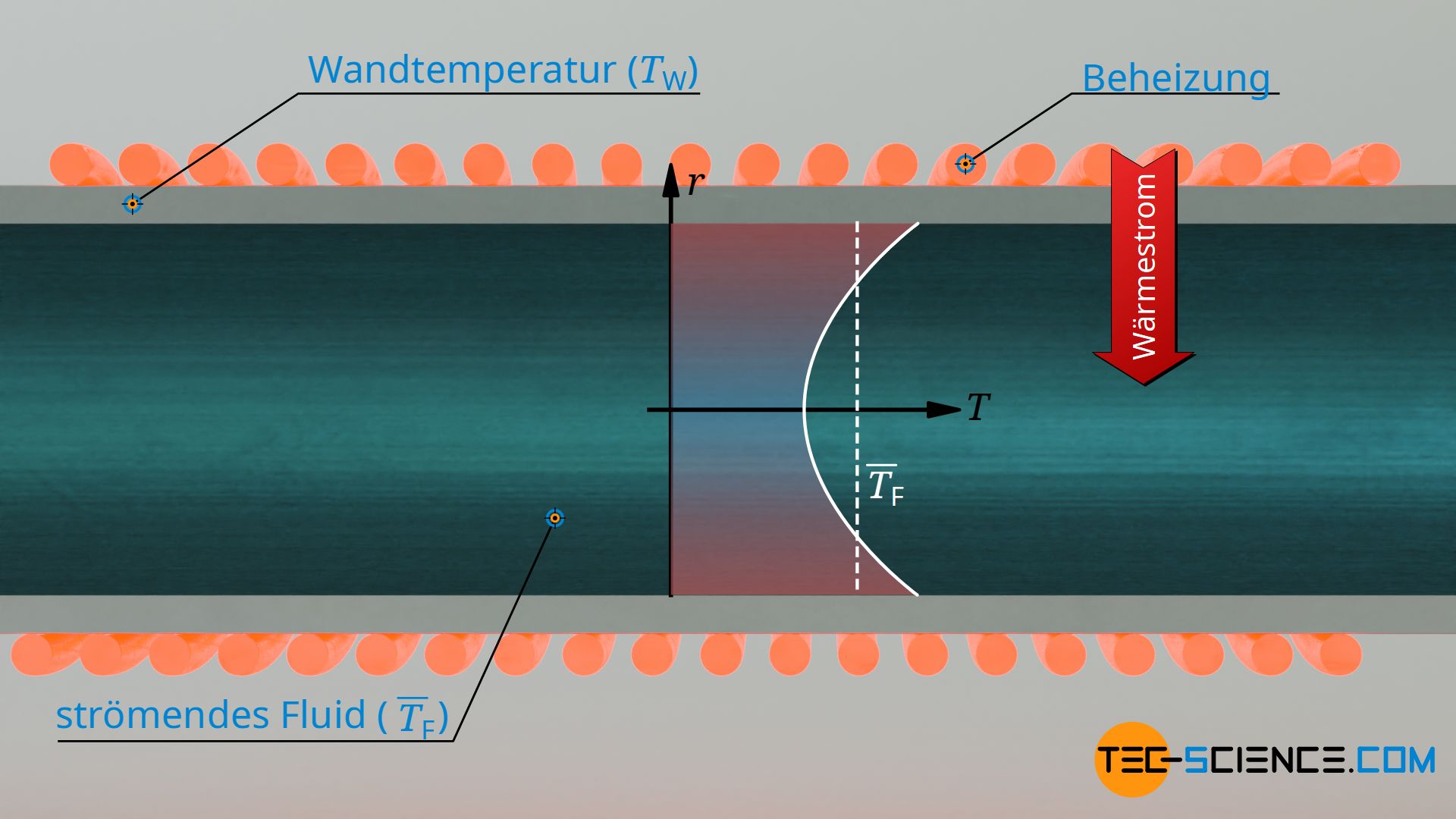
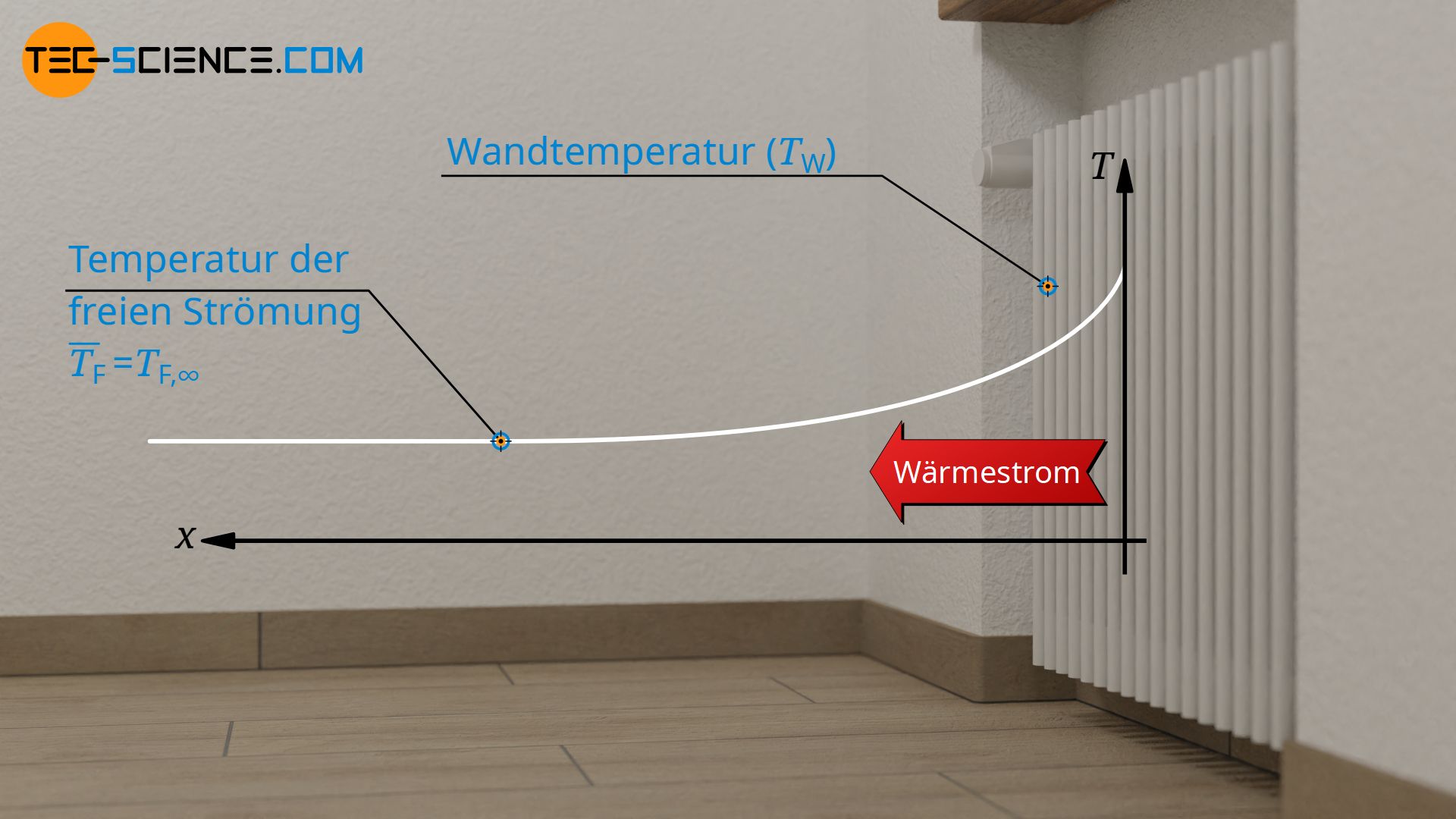
Darin bezeichnet q* die Wärmestromdichte an der Wand, TF die Temperatur des strömenden Fluids und TW die Temperatur der festen Wand. Bei einer Rohrströmung bezieht sich Fluidtemperatur auf die adiabate Mischtemperatur, d.h. auf die Temperatur, wenn man das Fluid an der betrachteten Stelle ideal mischen würde. Bei einer offenen Strömung bezieht sich die Fluidtemperatur hingegen auf die Temperatur in der freien Strömung, d.h. in hinreichend großem Abstand zur Wand (TF=TF,∞).
Im Artikel zum Wärmeübergangskoeffizienten wurde die Bedeutung der Grenzschicht zwischen strömendem Fluid und fester Wand bereits ausführlich erläutert. Deshalb soll an dieser Stelle hierauf nur in aller Kürze eingegangen werden. Aufgrund der sogenannten Haftbedingung haftet das Fluid unmittelbar an der Wand (dies gilt nur auf vollständig ausgebildete Strömungen!). Somit ist ein Wärmetransport zwischen Wand und Fluid an dieser Stelle nur durch Wärmeleitung möglich. Gemäß des Fourierschen Gesetzes hat dabei der Temperaturgradient im Fluid entscheidenden Einfluss auf den Wärmestrom. Je größer der Temperaturgradient, desto höher der Wärmestrom bzw. die Wärmestromdichte:
\begin{align}
\label{qw}
& \boxed{\dot{q_\lambda} =- \lambda_F \cdot \left(\frac{\text{d}T_F}{\text{d}y}\right)_\text{Wand}} ~~~~~\text{Fouriersches Gesetz} \\[5px]
\end{align}
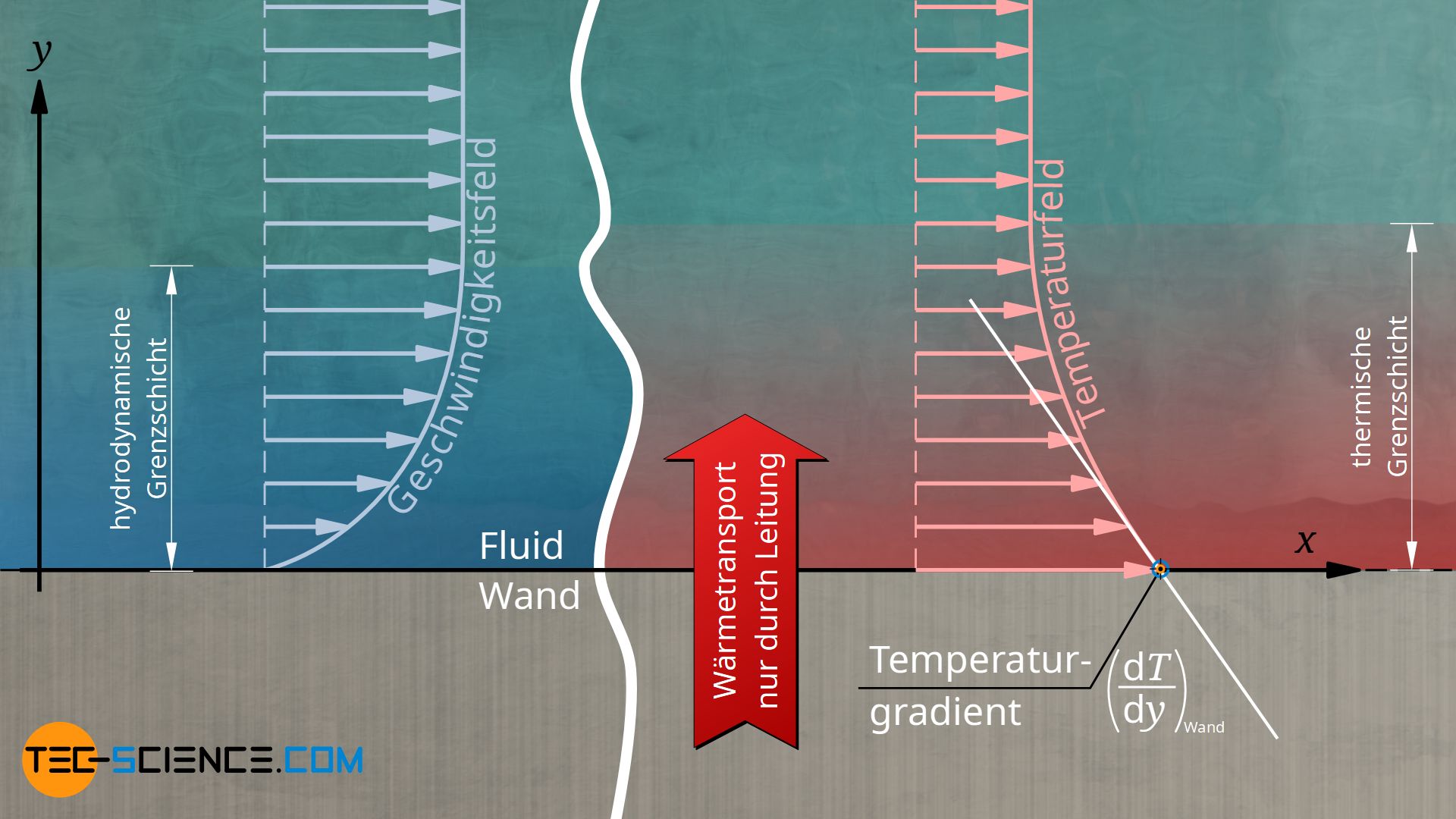
Darin bezeichnet λF die Wärmeleitfähigkeit des Fluids und dTF/dy|Wand den Temperaturgradienten des Fluids unmittelbar an der Wand. Unter der Bedingung qλ*=qα* folgt für den Wärmeübergangskoeffizienten α aus Gleichung (\ref{qq}) die unten hergeleitete Beziehung. Beachte, dass die Wärmestromdichten an der Wand identisch sein müssen, denn es kann nur so viel Wärme durch das Fluid hindurch geleitet werden, wie die Wand auch abgibt.
\begin{align}
&\alpha = \frac{\dot q_\alpha}{T_W-\overline{T_F}} \\[5px]
\label{wand}
&\boxed{\alpha = \frac{- \lambda_F \cdot \left(\frac{\text{d}T_F}{\text{d}y}\right)_\text{Wand}}{T_W-\overline{T_F}}}\\[5px]
\end{align}
Im Vergleich zu einem ruhenden Fluid (keine Konvektion) beeinflusst aber nun eine Strömung das Temperaturfeld im Fluid entscheidend, was wiederum Auswirkungen auf den Temperaturgradienten und somit auf den gesamten (konvektiven) Wärmeübergang hat. Unter vereinfachten Bedingungen betrachten wir hierzu eine beheizte Wand, die an einer Stelle x Wärme auf ein vorbeiströmendes Fluid überträgt. Durch das Strömen des Fluids wird die auf das Fluid übertragene Wärme relativ schnell abtransportiert und kühleres Fluid strömt nach. Würde sich das Fluid hingegen nicht bewegen, so würde sich die Wärme sozusagen aufstauen und das Fluid würde sich relativ stark erwärmen.
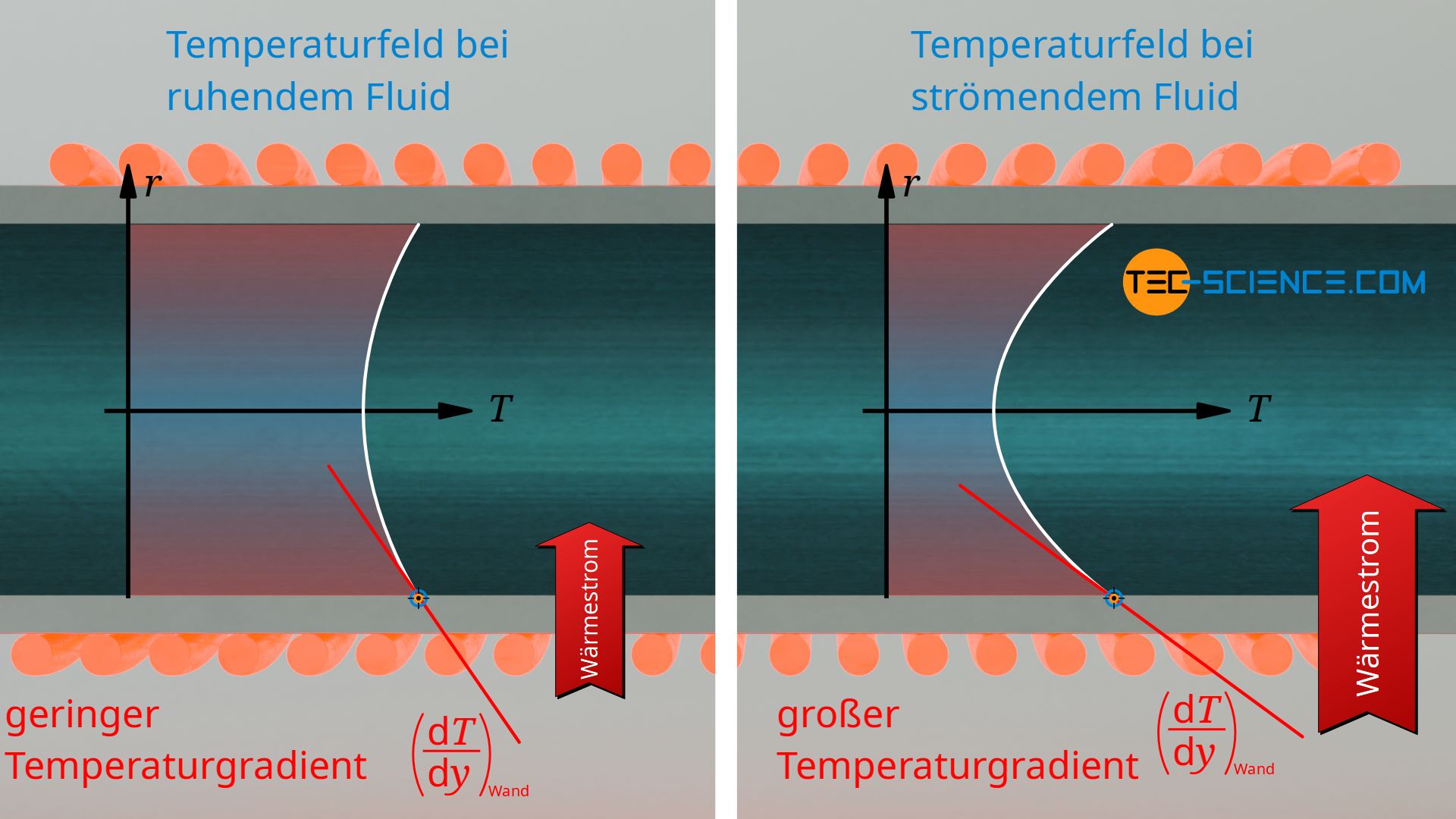
Salopp formuliert, ist also ein strömendes Fluid nahe einer beheizten Wand kühler als ein ruhendes Fluid. Bei Konvektionsströmungen fällt unmittelbar an der Wand somit die Temperatur im Fluid stärker ab. Dies wiederum bedeutet gemäß des Fourierschen Gesetzes einen größeren Wärmestrom. Besonders große Temperaturgradienten erhält man zudem, wenn die Strömung turbulent ist, sodass sich das Fluid durchmischt und die Wärme nochmals deutlich schneller von der Wand abtransportiert werden kann.
Definition der Nusselt-Zahl
Wie soeben erklärt, erfolgt der Wärmetransport unmittelbar an der Wand ausschließlich durch Wärmeleitung. Eine solche Wärmeleitung findet aber nicht nur an der Wand statt, sondern letztlich im gesamten Fluid. Der prinzipielle Mechanismus der Wärmeleitung ist ja nicht dadurch außer Kraft gesetzt, nur weil sich das Fluid bewegt. Allerdings dominiert in größerer Entfernung zur Wand der Wärmetransport durch die Strömung. Wie die obere Betrachtung der angeströmten Platte zeigte, beeinflussen sich beide Arten der Wärmeübertragung aber gegenseitig, dadurch dass sich das Temperaturfeld durch die Strömung ändert.
Zusammenfassend kann also festgehalten werden, dass Konvektion auf zwei wesentlichen Wärmeübertragungsmechanismen beruht:
- Wärmeleitung durch die ungeordnete Wärmediffusion der Teilchen (vor allem in der Nähe der Wand stark ausgeprägt, wo das Fluid praktisch ruht)
- Wärmeströmung in Form einer geordneten Bewegung der gesamten Fluidmenge (vor allem in größerer Entfernung zur Wand stark ausgeprägt)
- (Wärmestrahlung spielt nur bei extrem hohen Temperaturdifferenzen eine Rolle und wird daher vernachlässigt)
Beide Mechanismen zusammen bilden den makroskopisch beobachtbaren Wärmeübergang durch Konvektion, der durch Gleichung (\ref{qq}) sozusagen makroskopisch beschrieben wird und durch Gleichung (\ref{qw}) aber auch mikroskopisch ausgedrückt werden kann.
Das Verhältnis zwischen dem konvektiven Wärmeübergang („α“) im Vergleich zu einer reinen Wärmeleitung („λF„), wird durch die dimensionslose Nusselt-Zahl „Nu“ beschrieben:
\begin{align}
\label{nu}
&\boxed{Nu:= \frac{\alpha}{\lambda_F}L} ~~~~~\text{Nusselt-Zahl} \\[5px]
\end{align}
Darin bezeichnet L die sogenannte die charakteristische Länge des Systems, welche den Einfluss der Systemgröße auf den Wärmeübergang beschreibt. Im Fall eines Rohres entspräche die charakteristische Länge dem Rohrdurchmesser. Bei Betrachtung des Wärmeübergangs an einer Platte ist die charakteristische Länge mit der Plattenlänge in Strömungsrichtung gleichzusetzen.
Die Nusselt-Zahl beschreibt salopp formuliert das Verhältnis von konvektivem Wärmeübergang im Vergleich zu einer reinen Wärmeleitung!
An dieser Stelle wird häufig mit Beispielen versucht eine anschauliche Interpretation der Nusselt-Zahl als Verhältnis von Konvektion zu Wärmeleitung zu geben. In speziellen Situationen mag dies durchaus möglich und sinnvoll sein. In den meisten Fällen führt dies unserer Meinung nach aber mehr zu Verwirrungen als es zum wirklichen Verständnis beiträgt.
Deshalb möchten wir von einer solchen Interpretation Abstand nehmen und einen anderen Ansatz verfolgen. Dieser zeigt sich, wenn man den Wärmeübergangskoeffizienten gemäß Gleichung (\ref{wand}) in die Definition der Nusselt-Zahl (\ref{nu}) einsetzt:
\begin{align}
\require{cancel}
&Nu= \frac{\alpha}{\lambda_F}L \\[5px]
&Nu= \underbrace{\frac{- \cancel{\lambda_F} \cdot \left(\frac{\text{d}T_F}{\text{d}y}\right)_\text{Wand}}{T_W-\overline{T_F}}}_{\alpha} \cdot \frac{L}{\cancel{\lambda_F}} \\[5px]
\label{nutint}
&\boxed{Nu= \color{red}{\frac{\left(\frac{\text{d}T_F}{\text{d}y}\right)_\text{Wand}}{\overline{T_F}-T_W}} \cdot L} \\[5px]
\end{align}
Der rot markierte Term entspricht einem normierten Temperaturgradienten an der Wand. Die Nusselt-Zahl kann deshalb als Maß für den dimensionslosen Temperaturgradienten an der Wand interpretiert werden. Und umso größer dieser Temperaturgradient desto höher der Wärmestrom. Später werden wir noch zeigen, dass für ausgebildete Rohrströmungen dieser dimensionslose Temperaturgradient unter bestimmten Randbedingungen konstant ist. Dies gilt dann auch für die Nusselt-Zahlen.
Die Nusselt-Zahl ist ein Maß für den (entdimensionierten) Temperaturgradienten des Fluids an der Wand!
Technische Bedeutung der Nusselt-Zahl
So unanschaulich es zunächst auch klingen mag, erfährt die Nusselt-Zahl ihre wahre Begründung erst durch die Ähnlichkeitstheorie. Denn nur wenn man in unterschiedlich großen Systemen dieselben Nusselt-Zahlen erhält, kann man auch von physikalisch ähnlichen Wärmetransportvorgängen ausgehen. Später kann dann über die charakteristische Länge des Systems L und der Wärmeleitfähigkeit des Fluids λF der Wärmetransport in Form des Wärmeübergangskoeffizient α ganz konkret ermittelt werden:
\begin{align}
\label{alpha}
&\boxed{\alpha = Nu \cdot \frac{\lambda_F}{L}} \\[5px]
\end{align}
Die Nusselt-Zahl ist eine dimensionslose Ähnlichkeitskenngröße zur Beschreibung des konvektiven Wärmeübergangs. Nur bei identischen Nusselt-Zahlen erhält man unabhängig der Systemgröße stets physikalisch ähnliche Wärmeübergänge.
Während sich also der Wärmeübergangskoeffizient α immer auf einen konkreten Anwendungsfall bezieht (abhängig von der Größe des Systems), beschreibt die Nusselt-Zahl Nu völlig unabhängig des tatsächlichen Falls den konvektiven Wärmetransport (unabhängig von der Größe des Systems).
Die Nusselt-Zahl hat deshalb bspw. in der Chemietechnik große Bedeutung. Bevor chemische Prozesse nämlich durchgeführt oder Anlagen im realen Maßstab gebaut werden, werden diese zunächst in verkleinertem Maßstab erprobt bzw. erforscht (z.B. im Labor oder Technikum). Um dabei dieselben bzw. ähnlichen Wärmeübergänge wie später in der realen Größe zu erhalten, muss die Nusselt-Zahl in allen Maßstäben dieselbe sein. Man ermittelt also im kleinen Maßstab die entsprechende Nusselt-Zahl und wendet diese dann auf den realen Maßstab an (Scale-Up).
Die Nusselt-Zahl stellt im Falle des konvektiven Wärmeübergangs die Verbindung zwischen Modell und realem System her!
Lokale und mittlere Nusselt-Zahl
Betrachtet man den Wärmeübergang nur an einer bestimmten Stelle x im System (z.B. an einem Punkt in einem durchströmten Rohr), dann spricht man in diesem Zusammenhang auch von der lokalen Nusselt-Zahl. Die lokale Nusselt-Zahl beschreibt somit den lokalen Wärmeübergangskoeffizienten und damit die lokale Wärmestromdichte.
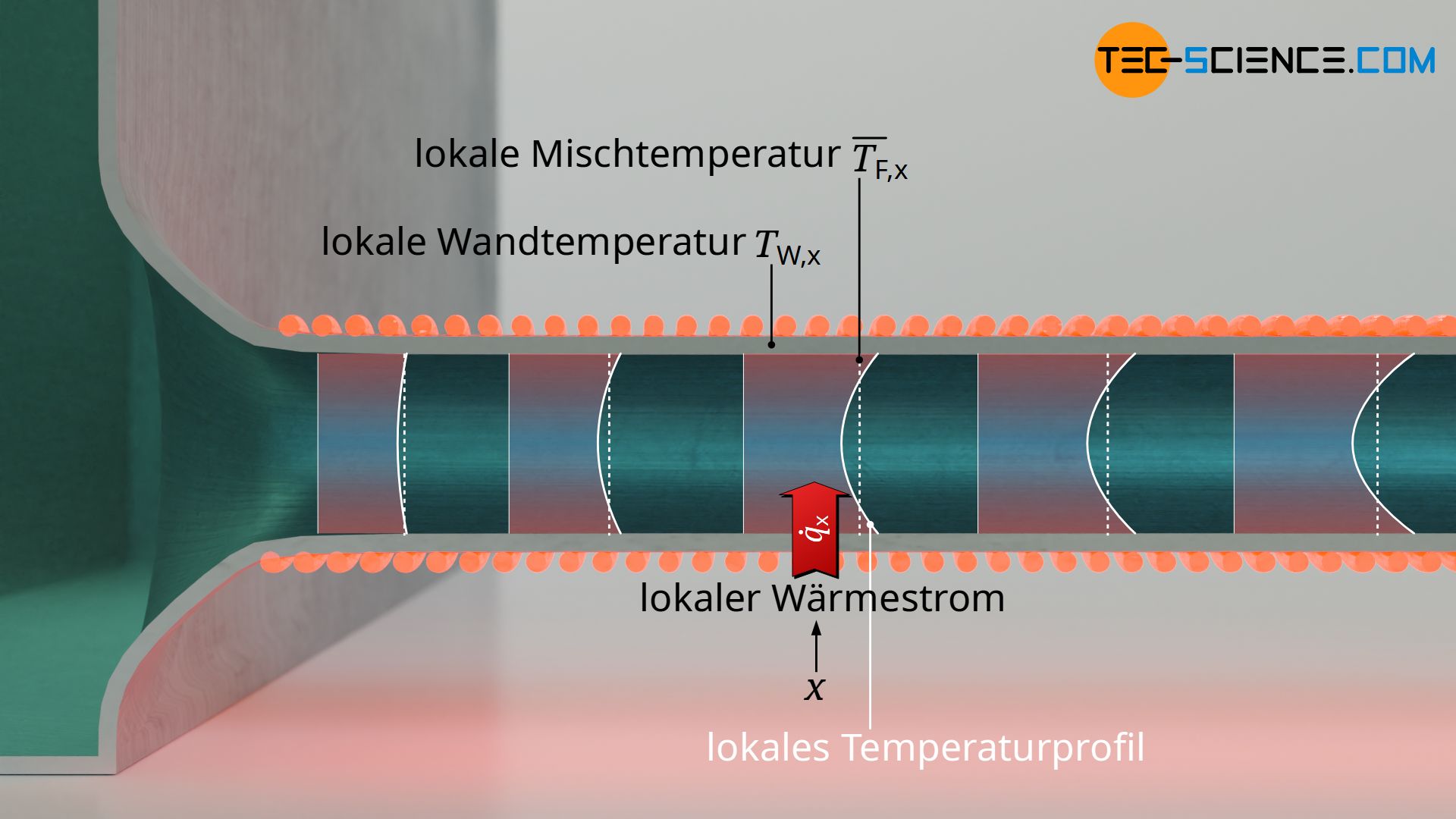
Man kann den Wärmeübergang aber auch auf das gesamte System an sich beziehen bzw. auf eine bestimmten Abschnitt. Im Falle einer Rohrströmung also nicht mehr auf eine spezielle Stelle im Rohr, sondern auf einen längeren Rohrabschnitt l. Man spricht dann von der mittleren Nusselt-Zahl, die den mittleren Wärmeübergangskoeffizienten gemittelt über die betrachtete Länge angibt. In diesem Fall erhält man die mittlere Wärmestromdichte über das gesamte Rohr.
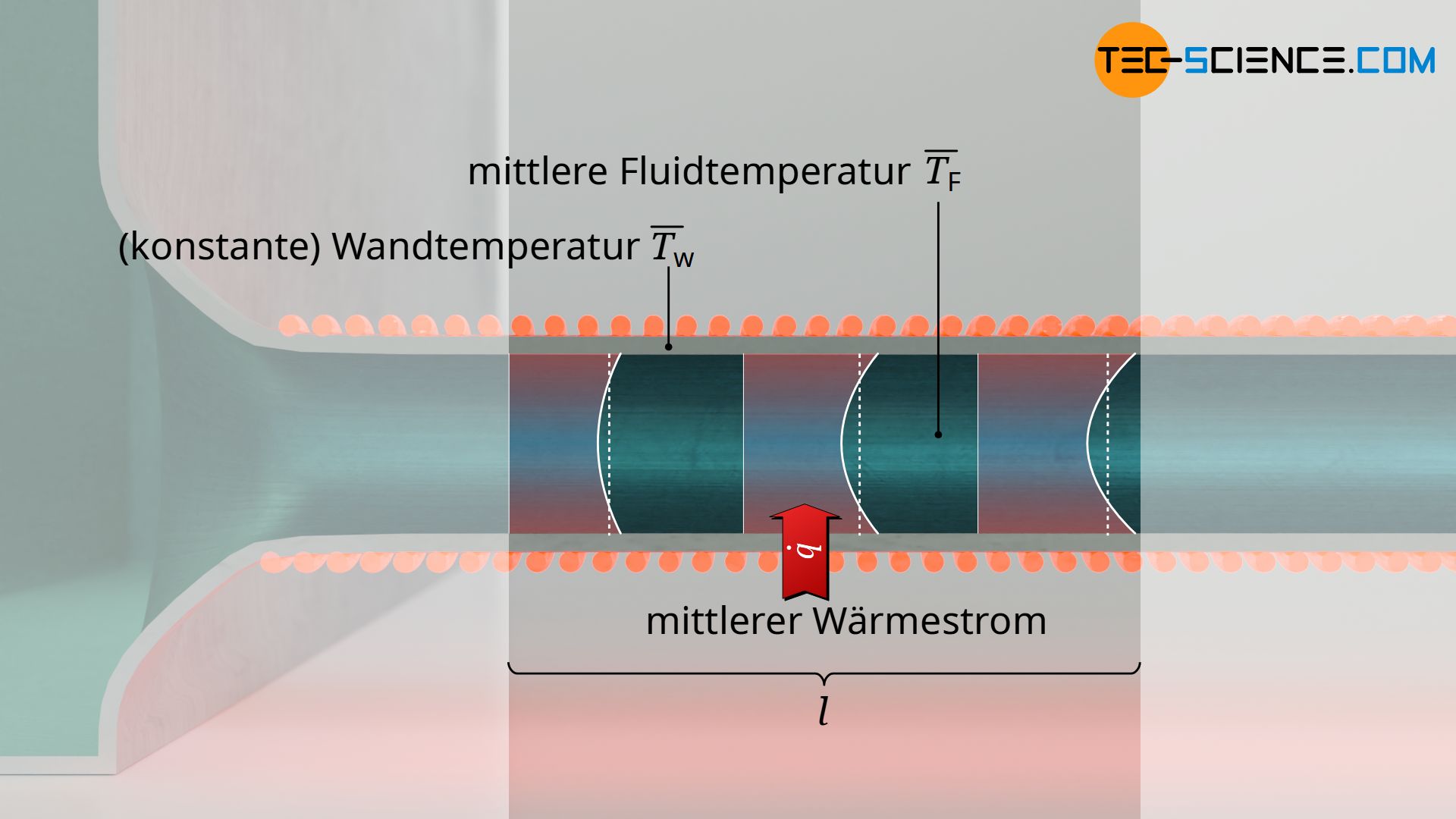
Die mittleren Nusselt-Zahlen erhält man also durch Integration der lokalen Nusselt-Zahlen über das gesamte System hinweg. Bei einem Rohr entspräche dies der Integration über die gesamte Rohrlänge und bei einer Platte über die gesamte Oberfläche.
Im Artikel Berechnung der Nusselt-Zahlen wird auf die Berechnung der lokalen und mittleren Nusselt-Zahlen von umströmten Platten und durchströmten Rohren näher eingegangen.
Dimensionslose Temperatur und Nusselt-Zahl im Zusammenhang mit Rohrströmungen
Das grundsätzliche „Problem“ bei der Beschreibung des Temperaturprofils im Inneren des Rohres ist, dass sich dieses entlang des Rohres ändert. Denn schließlich wird bei einem isotherm beheizten Rohr permanent Wärme auf das Fluid übertragen, welches sich dadurch erwärmt. Dies bedeutet, dass die Temperaturdifferenz zwischen einem Punkt im Fluid im Abstand r zur Rohrachse (TF) und der Wand (TW) eine Funktion von r und der Position x ist:
\begin{align}
&f(x,r) = T_F-T_W \\[5px]
\end{align}
Bezieht man diese Funktion allerdings auf die Differenz zwischen adiabater Mischtemperatur an der betrachteten Stelle x (TF) und konstanter Wandtemperatur TW, dann ist diese dimensionslose Fluidtemperatur θF bei thermisch und hydrodynamisch ausgebildeter Strömung unabhängig der Position im Rohr. Eine Strömung bezeichnet man dann als ausgebildet, wenn sich die Dicke der Grenzschichten nicht mehr ändert.
\begin{align}
&\boxed{\theta_F:= \frac{T_F-T_W}{\overline{T_F}-T_W}} ~~~~~\text{dimensionslose Fluidtemperatur}\\[5px]
\end{align}
Als ausgebildete Strömung bezeichnet man eine Strömung, bei der sich die Dicke der Grenzschichten nicht mehr ändern!

Beachte, dass die Wandtemperatur TW in dieser Gleichung eine Konstante ist, während die Fluidtemperatur TF sowohl von r als auch von x abhängig ist. Die Mischtemperatur ist hingegen nur eine Funktion des Ortes x:
\begin{align}
&\theta_F(r) = \frac{T_F(r,x)-T_W}{\overline{T_F}(x)-T_W} \\[5px]
\end{align}
Man hat also sowohl im Zähler des Bruchs eine Abhängigkeit von x als auch im Nenner. Aufgrund der Bildung des Quotienten eliminiert diese Abhängigkeit des Ortes sozusagen, sodass dieser Ausdruck tatsächlich keine Funktion des Ortes mehr ist. Der Beweis soll an dieser Stelle nicht erbracht werden. Man kann aber unter dieser Voraussetzung zeigen, dass die Nusselt-Zahl unabhängig von x ist (und somit auch der Wärmeübergangskoeffizient).
Hierzu bestimmten wird durch Ableiten der oberen Gleichung nach r den dimensionslosen Temperaturgradienten. Dabei ist zu beachten, dass der blau markierte Term während der (partiellen) Ableitung bzgl. r als konstanter Faktor zu betrachten ist, da dieser Term keine Funktion von r ist. Zudem ist die Ableitung der Wandtemperatur TW nach r Null, da die Wandtemperatur eine Konstante ist.
\begin{align}
&\frac{\text{d} \theta_F(r)}{\text{d}r}= \color{blue}{\frac{1}{\overline{T_F}(x)-T_W}} \cdot \frac{\text{d}\left[T_F(r,x)-T_W\right]}{\text{d}r} \\[5px]
&\frac{\text{d} \theta_F(r)}{\text{d}r}= \color{blue}{\frac{1}{\overline{T_F}(x)-T_W}} \cdot \left[\frac{\text{d}T_F(r,x)}{\text{d}r} – \underbrace{\frac{\text{d}(T_W)}{\text{d}r}}_{=0} \right]\\[5px]
&\frac{\text{d} \theta_F(r)}{\text{d}r}= \color{blue}{\frac{1}{\overline{T_F}(x)-T_W}} \cdot \frac{\text{d}T_F(r,x)}{\text{d}r}\\[5px]
\end{align}
Für den dimensionslosen Temperaturgradienten an der Wand gilt somit:
\begin{align}
&\left(\frac{\text{d} \theta_F(r)}{\text{d}r}\right)_\text{Wand}= \frac{\left(\frac{\text{d}T_F(r,x)}{\text{d}r}\right)_\text{Wand}}{\overline{T_F}(x)-T_W} \\[5px]
\end{align}
Verzichten wir an dieser Stelle auf die Angabe der Argumente,
\begin{align}
&\left(\frac{\text{d} \theta_F}{\text{d}r}\right)_\text{Wand}= \color{red}{\frac{\left(\frac{\text{d}T_F}{\text{d}r}\right)_\text{Wand}}{\overline{T_F}-T_W}} \neq f(x)\\[5px]
\end{align}
dann zeigt sich sofort, dass der Ausdruck auf der rechten Seite gerade dem rot markierten Term in Gleichung (\ref{nutint}) entspricht (die Variable y entspricht in diesem Fall dem Radius r und die charakteristische L dem Rohrinnendurchmesser d). Wie die linke Seite dieser Gleichung allerdings zeigt, ist dieser Term nicht von x abhängig und somit auch nicht die Nusselt-Zahl:
\begin{align}
&\boxed{Nu= \left(\frac{\text{d} \theta_F}{\text{d}r}\right)_\text{Wand} \cdot d} \neq Nu(x)\\[5px]
\end{align}
Beachte, dass das dimensionslose Temperaturprofil bzw. die Nusselt-Zahl und der Wärmeübergangskoeffizient nur unter folgenden Bedingungen unabhängig der Position x ist:
- thermisch und hydrodynamisch ausgebildete, laminare Rohrströmung (siehe auch Hagen-Poiseuille-Strömung)
- konstante Wandtemperatur oder konstanter Wärmestromdichte
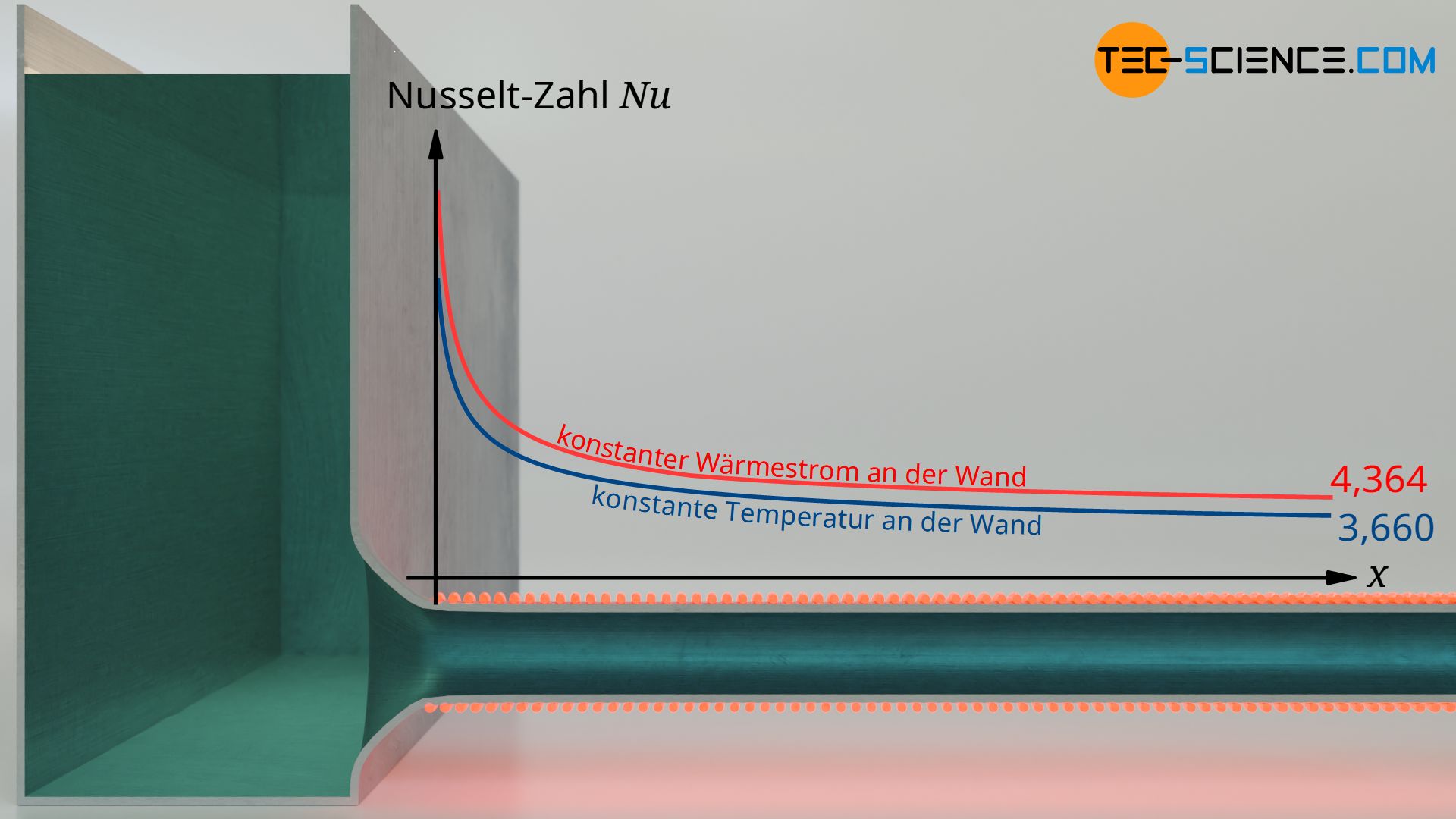
Umso länger ein Rohr ist, umso besser wird die Bedingung der vollständig ausgebildeten Rohrströmung erfüllt sein. Die Nusselt-Zahl strebt für lange Rohre deshalb einem Grenzwert entgegen. Diese Asymptote kann man mit Hilfe von numerischen Verfahren ermitteln. Je nach Randbedingung erhält man folgende Grenzwerte für die lokalen bzw. mittleren Nusselt-Zahlen:
\begin{align}
\label{366}
&\boxed{Nu_{\infty}= 3,660} &&~~~\text{bei konstanter Wandtemperatur}\\[5px]
\label{4364}
&\boxed{Nu_{\infty}= 4,364} &&~~~\text{bei konstanter Wärmestromdichte an der Wand}\\[5px]
\end{align}
Beachte, dass eine vollständig ausgebildete Rohrströmung theoretisch eben nur für sehr lange Rohre bzw. in hinreichend großem Abstand zum Rohranfang gegeben ist. Daher ist die lokale Nusselt-Zahl im Allgemeinen sehr wohl abhängig von x bzw. die mittlere Nusselt-Zahl abhängig von der Rohrlänge l. Mehr hierzu im Artikel Berechnung der Nusselt-Zahlen.