Herleitung der Bernoulli-Gleichung

Die Bernoulli-Gleichung beschreibt die Beziehung zwischen statischem, dynamischem und hydrostatischem Druck für nicht-viskose und inkompressible Fluide.

Statischer, dynamischer und hydrostatischer Druck

Aufgrund des wirkenden Drucks in ruhenden Fluiden wird eine Kraft auf Grenzflächen ausgeübt. Diese Kraft ist in der Lage Arbeit zu verrichten, z.B. wenn diese auf den Kolben in einem Zylinder wirkt. Im Artikel Bernoulli-Effekt wurde bereits ausführlich erläutert, dass Druck deshalb als eine volumenspezifische Energie interpretiert werden kann. Der Druck gibt an wie viel potentielle Energie pro Volumeneinheit in einem Fluid vorhanden ist und in mechanische Arbeit umgewandelt werden kann:

\begin{align}
\label{p}
& \boxed{p= \frac{\Delta W}{\Delta V}} \\[5px]
\end{align}

Ein makroskopisch ruhendes Fluid kann lediglich aufgrund des statischen Drucks Arbeit verrichteten, d.h. der Druck der aufgrund der ungeordneten mikroskopischen Bewegung der Moleküle entsteht, wenn diese auf eine Grenzfläche prallen (siehe auch Artikel Druck in Gasen). Ist in einem Fluid aber zusätzlich noch eine makroskopische Strömung vorhanden (geordnete makroskopische Bewegung), dann kann das Fluid auch aufgrund der damit verbundenen kinetischen Energie Arbeit verrichten. Bezieht man diese kinetische Energie auf das Fluidvolumen, dann kann man der kinetischen Energie gemäß Gleichung (\ref{p}) ebenfalls einen Druck zuordnen. Im Gegensatz zum statischen Druck, spricht man in diesem Fall vom dynamischen Druck. Salopp formuliert gilt also:

Der statische Druck ist mit der ungeordneten mikroskopischen Bewegung der Moleküle verbunden, während der dynamische Druck mit der geordneten makroskopischen Bewegung des strömenden Fluids verknüpft ist!

Je nach Bezugsniveau besitzt ein Fluid zudem noch Lageenergie, die ebenfalls in Arbeit umgewandelt werden kann. Diese Energie nutzt man bspw. in durch Aufstauung von Seen in Wasserkraftwerken. Die pro Volumeneinheit enthaltene Lageenergie entspricht gemäß Gleichung (\ref{p}) wiederum einem bestimmten Druck. Dieser Druck wird hydrostatischer Druck genannt!

Wird einer Strömung von außen keine Energie zugeführt, dann muss aus Gründen der Energieerhaltung die Summe aus statischer Energie, kinetischer Energie und Lageenergie konstant bleiben. Bei horizontalen Strömungen oder bei Strömungen von Fluiden mit geringer Dichte (z.B. Gasen) sind Lageenergien zu vernachlässigen. In diesem Fall bedeutet eine Zunahme der kinetischen Energie somit unweigerlich eine Abnahme der statischen Energie.

Ein solcher Fall tritt bspw. bei horizontalen Rohrströmungen ein, wenn sich das Rohr im Querschnitt verengt. Aufgrund der Kontinuitätsbedingung kann sich keine Masse im Rohr ansammeln und auch vernichtet werden. An jeder Stelle des Rohres muss innerhalb einer bestimmten Zeit somit dieselbe Masse strömen (Massenerhaltung). Bei kleinen Querschnitten muss somit die Strömungsgeschwindigkeit größer sein, damit pro Zeiteinheit dieselbe Masse hindurch strömen kann.

Eine Abnahme des Querschnitts bedeutet somit unweigerlich eine Erhöhung der Strömungsgeschwindigkeit. Die damit verbundene Erhöhung der kinetischen Energie kann nur aus der statischen Energie stammen, solange von außen keine Energie zugeführt wird (bspw. durch eine Pumpe). Der statische Druck sinkt somit zu Gunsten des dynamischen Drucks. Im Artikel Bernoulli-Effekt wurde auf dieses Phänomen, dass der Druck in strömenden Fluiden mit zunehmender Strömungsgeschwindigkeit abnimmt, bereits ausführlich eingegangen.

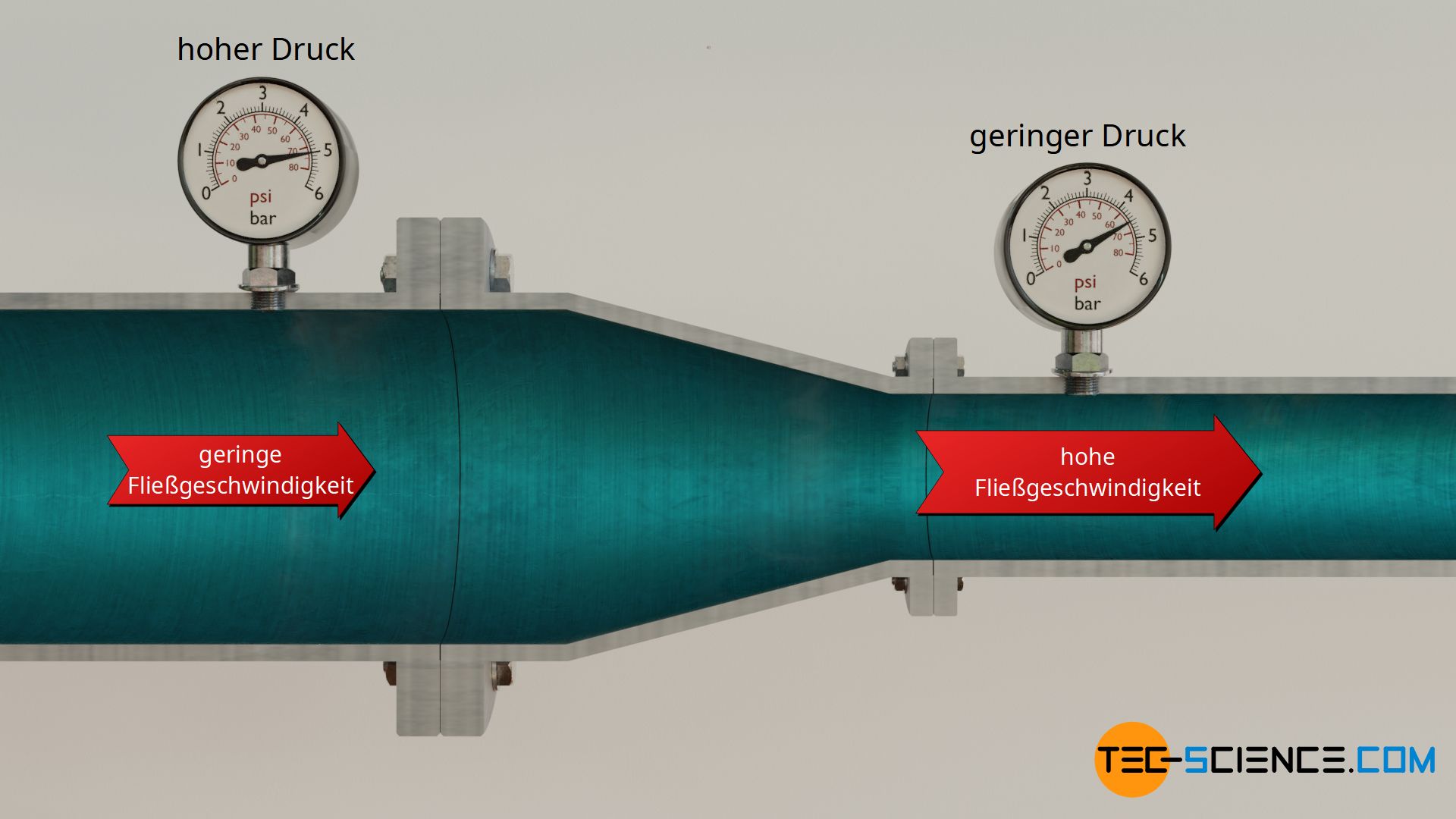
Wie bereits erwähnt müssen Lageenergien im Allgemeinen zusätzlich noch berücksichtigt werden, wenn das Fluid eine bestimmte Höhendifferenz überwindet. Der sich dabei ergebende mathematische Zusammenhang zwischen Höhendifferenz, Strömungsgeschwindigkeit und statischem Druck soll im Folgenden hergeleitet werden.

Herleitung der Bernoulli-Gleichung

Für die Herleitung der Zusammenhänge zwischen den unterschiedlichen Druckarten, betrachten wir ein reibungsfrei strömendes inkompressibles Fluid in einem Rohr. Das Rohr habe dabei einen veränderlichen Querschnitt und überwinde einen bestimmten Höhenunterschied.

Druckenergie (Ein- und Ausschiebeenergie)

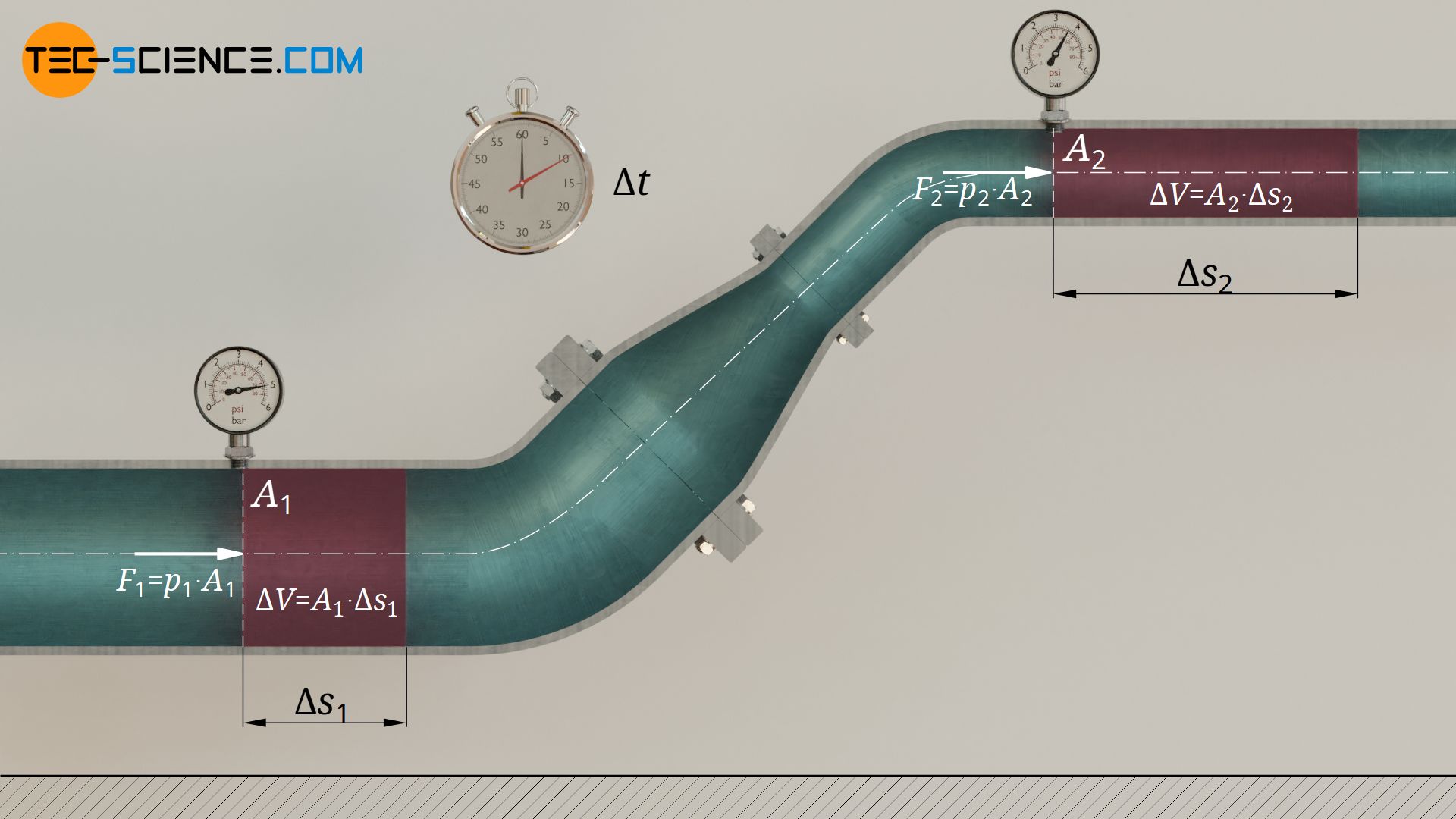
Betrachten wir zunächst den unteren Teil des Rohrabschnitts im Punkt 1. Dort wirke der statische Druck p₁. Innerhalb einer bestimmten Zeit drückt dieser eine bestimmte Fluidmasse Δm durch den Rohrquerschnitt A₁. Die Strecke, um die das betrachtete Fluidelement dabei verschoben wird, betrage Δs₁. Die Druckenergie W₁, mit der das Fluidelement aufgrund des statischen Drucks eingeschoben wird (Einschiebeenergie), ist abhängig vom eingeschobenen Fluidvolumen ΔV:

\begin{align}
& W_1 = F_1 \cdot \Delta s_1= p_1 \underbrace{A_1 \cdot \Delta s_1}_{\Delta V} \\[5px]
& \underline{W_1 = p_1 \Delta V} ~~~~~\text{Einschiebeenergie}\\[5px]
\end{align}

Nun betrachten wir den oberen Teil des Rohres im Punkt 2. Dort wirkt aufgrund der im Abschnitt zuvor erläuterten Zusammenhänge ein geringerer statischer Druck p₂. Aufgrund der Massenerhaltung muss innerhalb der betrachten Zeit aber dennoch dieselbe Fluidmasse durch den verkleinerten Querschnitt A₂ geschoben werden (Kontinuitätsbedingung). Da es sich um inkompressibles Fluid handelt, strömt folglich dasselbe Fluidvolumen ΔV oben aus dem betrachteten Rohrabschnitt aus wie unten einströmt.

Bei verkleinertem Querschnitt A₂ bedeutet dies aber eine größere Verschiebestrecke Δs₂ und somit eine höhere Strömungsgeschwindigkeit! Aufgrund des dort wirkenden statischen Drucks p₂ wird das Fluidelement mit folgender Druckenergie W₂ wieder aus dem betrachteten Rohrabschnitt ausgeschoben (Ausschiebeenergie):

\begin{align}
& W_2 = F_2 \cdot \Delta s_2= p_2 \underbrace{A_2 \cdot \Delta s_2}_{\Delta V} \\[5px]
& \underline{W_2 = p_2 \Delta V} ~~~~~\text{Ausschiebeenergie}\\[5px]
\end{align}

Beschleunigungsarbeit und Hubarbeit

In der Praxis wird man nun feststellen, dass die Energie W₁ mit der das Fluidelement in den Rohrabschnitt eingeschoben wurde größer ist als die Energie W₂ mit der es wieder ausgeschoben wird. Dies hat folgenden Grund: Ein Teil der Einschiebeenergie musste nämlich zum einen dazu verwendet werden das Fluidelement zu beschleunigen (Aufwenden von Beschleunigungsarbeit) und zum anderen wurde Energie benötigt, um das Fluid entgegen der Schwerkraft anzuheben (Aufwenden von Hubarbeit). Die Einschieenergie, abzüglich der hieraus verrichteten Beschleunigungsarbeit und Hubarbeit, ergibt die beim Austritt verbleibende Ausschiebeenergie. Oder anders ausgedrückt: Die Differenz der Verschiebeenergien entspricht der Summe aus Beschleunigungsarbeit ΔW_b und Hubarbeit ΔW_h:

\begin{align}
\label{a}
& \boxed{W_1 – W_2 = \Delta W_\text{b} + \Delta W_\text{h}} \\[5px]
\end{align}

Die für den Beschleunigungsvorgang des Fluidelementes von v₁ auf v₂ benötigte Energie bestimmt sich aus der Differenz der kinetischen Energie im Punkt 2 und Punkt 1 (Beachte: Δm=ϱ⋅ΔV):

\begin{align}
& \Delta W_\text{b} = W_\text{kin,2} -W_\text{kin,1} \\[5px]
& \underline{\Delta W_\text{b} = \frac{1}{2} \cdot \rho \Delta V \cdot v_2^2~ – \frac{1}{2} \cdot \rho \Delta V \cdot v_1^2} \\[5px]
\end{align}

Für die aufzuwendende Hubarbeit, um das Fluidelement von der Höhe h₁ auf die Höhe h₂ anzuheben, gilt:

\begin{align}
& \Delta W_\text{h} = W_\text{Lage,2} – W_\text{Lage,1}\\[5px]
& \underline{\Delta W_\text{h} =\rho \Delta V \cdot g \cdot h_2 – \rho \Delta V \cdot g \cdot h_1}\\[5px]
\end{align}

Bernoulli-Gleichung

Werden die bisherigen Formeln in Gleichung (\ref{a}) eingesetzt, dann zeigt sich folgender Zusammenhang zwischen den Druckenergien, den kinetischen Energien und den Lageenergien an den beiden betrachteten Stellen:

\begin{align}
\label{1}
& \underbrace{p_1 {\Delta V} – p_2 {\Delta V}}_{\text{Druckenergien}} = \underbrace{\frac{1}{2} \rho {\Delta V} v_2^2 – \frac{1}{2} \rho {\Delta V} v_1^2}_{\text{kinetische Energien}} + \underbrace{\rho {\Delta V} g h_2 – \rho {\Delta V}g h_1}_{\text{Lageenergien}} \\[5px]
\end{align}

Alle Energieterme enthalten das Fluidvolumen. Man kann diese Gleichung deshalb durch das Fluidvolumen teilen und ist somit unabhängig davon:

\begin{align}
\label{2}
& p_1 – p_2 = \frac{1}{2} \rho v_2^2 – \frac{1}{2} \rho v_1^2 + \rho g h_2 – \rho g h_1 \\[5px]
\end{align}

Umstellen dieser Gleichung nach den Zustandsgrößen im Zustand 1 und im Zustand 2 liefert schließlich folgenden Zusammenhang, der auch als Bernoulli-Gleichung bezeichnet wird:

\begin{align}
& \boxed{p_1 + \frac{1}{2} \rho v_1^2 +\rho g h_1= p_2 + \frac{1}{2} \rho v_2^2 + \rho g h_2} ~~~\text{Bernoulli-Gleichung} \\[5px]
&\text{oder}\\[5px]
& \boxed{p + \frac{1}{2} \rho ~v^2 +\rho g h= \text{konstant}}=p_\text{ges} \\[5px]
\end{align}

Die in der Bernoulli-Gleichung enthaltenen Terme haben alle die Dimension eines Drucks. Der Term ½⋅ϱ⋅v², der mit der kinetischen Energie des Fluids verknüpft ist, nennt sich hydrodynamischer Druck oder auch nur dynamischer Druck. Der mit der Lageenergie verknüpfte Term ϱ⋅g⋅h wird hydrostatischer Druck genannt. In Abgrenzung hierzu wird der Druck p als statischer Druck bezeichnet.

Druckart	Term	Energetisch verknüpft mit
statischer Druck	p	Druckenergie (pro Einheit Fluidvolumen)
dynamischer Druck	½⋅ϱ⋅v²	kinetische Energie (pro Einheit Fluidvolumen)
hydrostatischer Druck	ϱ⋅g⋅h	Lageenergie (pro Einheit Fluidvolumen)

Im Artikel Aufgaben und Lösungen zur Bernoulli-Gleichung wird auf ausgewählte Beispiele zur Anwendung der Bernoulli-Gleichung näher eingegangen.

Die Bernoulli-Gleichung besagt im Prinzip nichts anderes, dass die Summe aus statischem Druck, dynamischem Druck und hydrostatischem Druck in einer reibungsfreien, inkompressiblen Strömung konstant ist (sofern keine Energie von außen zugeführt wird, bspw. durch eine Pumpe). Die konstante Summe dieser Drücke wird auch als Gesamtdruck p_ges bezeichnet. Für die Anwendung der Bernoulli-Gleichung kann man sich stets ein beliebiges Fluidelement vorstellen, das sich entlang einer Stromlinie bewegt. Die Bernoulli-Gleichung verknüpft auf dieser Stromlinie dann die Zustände zweier beliebiger Punkte miteinander.

Die Bernoulli-Gleichung besagt, dass entlang einer Stromlinie die Summe aus statischem Druck, dynamischem Druck und hydrostatischem Druck konstant ist. Sie gilt in dieser Form nur für eine reibungsfreie, inkompressible Strömung, ohne äußere Energiezufuhr.

Beachte, dass aufgrund der Viskosität von Fluiden keine Strömung völlig reibungsfrei ist, da die Fluidschichten hierdurch untereinander reiben. Diese Energiedissipation ist in der Praxis mit einem zusätzlichen (statischen) Druckverlust verbunden. Später hierzu mehr.

Wichtige Anmerkungen

Wichtig zu verstehen ist, dass die Bernoulli-Gleichung letztlich eine (volumenspezifische) Energiegleichung ist. Dies zeigt der Schritt von Gleichung (\ref{1}) auf Gleichung (\ref{2}), bei dem letztlich die verschiedenen Energieformen (Druckenergie, kinetische Energie und Lageenergie) auf das Fluidvolumen ΔV bezogen wurden. Die Bezeichnung als Druck für die einzelnen auftretenden Terme ist letztlich nur rein formaler Natur, da diese jeweils die Dimension eines Drucks haben. Man sollte aber stets im Hinterkopf haben, dass diese „Drücke“ letztlich auf Energien beruhen.

Vor allem die klassische Interpretation des Drucks als „Kraft pro Fläche“ führt ansonsten häufig zu Missverständnissen, besonders beim dynamischen Druck. Mit dieser Interpretation ist es nur sehr schwer bis unmöglich zu verstehen, warum bei Zunahme der Strömungsgeschwindigkeit der statische Druck sinkt. Fälschlicherweise geht man davon aus, dass eine hohe Strömungsgeschwindigkeit eine große „Kraft“ und damit einen hohen Druck bedeutet.

Vor dem Hintergrund der Interpretation als Energie wird aber sofort klar, dass sich die Zunahme der kinetischen Energie nur zu Lasten der Druckenergie vollziehen kann. Folglich sinkt der statische Druck mit Zunahme der Strömungsgeschwindigkeit! Dieses Phänomen bezeichnet man auch als Bernoulli-Effekt und wird im verlinkten Artikel näher erläutert.

Tatsächlich ist in diesem Zusammenhang auch der Begriff des hydrostatischen Drucks anders zu verstehen, als man ihn vielleicht vom hydrostatischen Druck einer Wassersäule her kennt. In der Bernoulli-Gleichung sollte der hydrostatische Druck nicht ohne Weiters als „Kraft pro Fläche“ interpretiert werden. In der Bernoulli-Gleichung kann einem Punkt in einer Strömung letztlich ein willkürlicher hydrostatischer Druck zugeordnet werden, je nach dem welches Bezugsniveau für die Höhe gewählt wird. Deshalb ändern sich aber natürlich nicht die „Kräfteverhältnisse“ im Fluid, nur weil man einen anderen Bezugspunkt wählt.

Der hydrostatische Druck ist in diesem Fall wiederum als Energie zu interpretieren, nämlich als Lageenergie, die pro Fluidvolumen in einem betrachteten Punkt vorhanden ist. Diese Lageenergie ist abhängig vom gewählten Bezugspunkt und deshalb auch der hierdurch definierte hydrostatische Druck.

Erweiterte Bernoulli-Gleichung mit Berücksichtigung von Verlusten

Da Druck letztlich eine Form der (volumen-spezifischen) Energie ist, bedeutet ein Verlust an Energie unweigerlich einen Druckverlust. Ein solcher Druckverlust tritt schon deshalb auf, weil jedes Fluid eine gewisse Zähigkeit besitzt; ausgedrückt durch die Viskosität. Die an einer Rohrwand befindlichen Fluidschichten haften aufgrund der sogenannten Haftbedingung dort an und die weiter innen liegenden Schichten müssen somit gegeneinander verschoben werden, wenn das Fluid strömen soll. Es kommt zu einer inneren Reibung im Fluid, die letztlich einen Energieverlust bedeutet und damit einen Druckverlust erzeugt (siehe auch Hagen-Poiseuille-Strömung).

Weitere Energieverluste treten bei turbulenten Strömungen infolge der Verwirbelungen auf. Dabei spielt die Rauheit der Rohrwand eine große Rolle. Auch in einzelnen Bauteilen in einem Rohrsystem wie in Ventilen, Rohrkrümmern, Verzweigungen, Aufweitungen, Reduzierungen, etc. treten Strömungsverluste und damit Druckverluste auf (mehr hierzu im Artikel Druckverlust in Rohrsystemen).

Die antreibende Energie einer Strömung, gegeben durch die Differenz der Verschiebeenergien W₂ und W₁ zwischen Ein- und Austritt eines betrachteten Strömungsabschnitts, muss im Allgemeinen also nicht nur die Strömung beschleunigen und entgegen der Schwerkraft anheben, sondern auch die Reibungsverluste ausgleichen. Gleichung (\ref{a}) ist deshalb um einen Verlustterm ΔW_V zu erweitern:

\begin{align}
& \boxed{W_1 – W_2 = \Delta W_\text{b} + \Delta W_\text{h} + \Delta W_\text{V}} \\[5px]
\end{align}

Gleichung (\ref{1}) stellt sich dann wie folgt dar:

\begin{align}
& \underbrace{p_1 {\Delta V} – p_2 {\Delta V}}_{\text{Druckenergien}} = \underbrace{\frac{1}{2} \rho {\Delta V} v_2^2 – \frac{1}{2} \rho {\Delta V} v_1^2}_{\text{kinetische Energien}} + \underbrace{\rho {\Delta V} g h_2 – \rho {\Delta V}g h_1}_{\text{Lageenergien}} + \underbrace{\Delta W_\text{V}}_{\text{Verlustenergie}}\\[5px]
\end{align}

Diese Gleichung durch das Fluidvolumen ΔV geteilt, ergibt dann die erweiterte Bernoulli-Gleichung mit Berücksichtigung von Energieverlusten:

\begin{align}
& \boxed{p_1 + \frac{1}{2} \rho v_1^2 +\rho g h_1= p_2 + \frac{1}{2} \rho v_2^2 + \rho g h_2 + \Delta p_\text{V}}~~~\text{mit}~\boxed{\Delta p_\text{V} = \frac{\Delta W_\text{V}}{\Delta V}} \\[5px]
\end{align}

Der Term W_V/ΔV entspricht dem Energieverlust pro Volumeneinheit und entspricht dem besagten Druckverlust Δp_V. Ein solcher Druckverlust macht sich grundsätzlich nur im statischen Druck bemerkbar, da die dynamischen und hydrostatischen Drücke durch die Strömungsgeschwindigkeiten bzw. Höhen vorgeben sind. Der statische Druck p₂ stromabwärts verringert sich im Vergleich zu einer verlustfreien Strömung um den Betrag des Druckverlustes:

\begin{align}
& p_2 = p_1 + \frac{1}{2} \rho \left(v_1^2-v_2^2\right) +\rho g (h_1-h_2) \color{red}{- \Delta p_\text{V}} \\[5px]
\end{align}