Herleitung der Navier-Stokes-Gleichungen

Die Navier-Stokes-Gleichungen dienen der Beschreibung von viskosen Strömungen. Erfahre in diesem Artikel mehr über die Herleitung dieser Gleichung.

Euler-Gleichung

Im Artikel Herleitung der Euler-Gleichung wurde folgende Gleichung zur Beschreibung der Bewegung von reibungsfreien Strömungen hergeleitet:

\begin{align}
&\boxed{\frac{\partial \vec v}{\partial t} + \left(\vec v \cdot \vec \nabla \right) \vec v + \frac{1}{\rho} \vec \nabla p = \vec g}~~~\text{Euler-Gleichung} \\[5px]
\end{align}

Die Annahme einer reibungsfreien Strömung bedeutet insbesondere die Vernachlässigung der Viskosität von Fluiden. In der Praxis hat jedoch jedes Fluid eine Viskosität (auch ideale Gase!). Diese Viskosität führt zu Reibungskräften innerhalb des Fluids. Die Berücksichtigung der Viskosität in der oberen Euler-Gleichung führt dann schließlich zu der Navier-Stokes-Gleichung.

Normalkräfte auf ein Fluidelement

Für die Herleitung der Navier-Stokes-Gleichungen betrachten wir ein Fluidelement und die hierauf wirkenden Kräfte. Wir beschränken uns dabei zunächst nur auf die Untersuchung der Bewegung in x-Richtung. Die Bewegung des Fluidelements wird zum einen durch die Druckkräfte beeinflusst, die auf die vordere und hintere Fläche wirken. Diese Druckkräfte stellen letztlich Normalspannungen dar und werden im Folgenden mit σ anstelle mit p bezeichnet. Wir werden später nämlich noch sehen, dass neben den Druckkräften weitere (viskositätsbedingte) Kräfte senkrecht auf die Flächen wirken und einen Beitrag zur Normalspannung leisten.

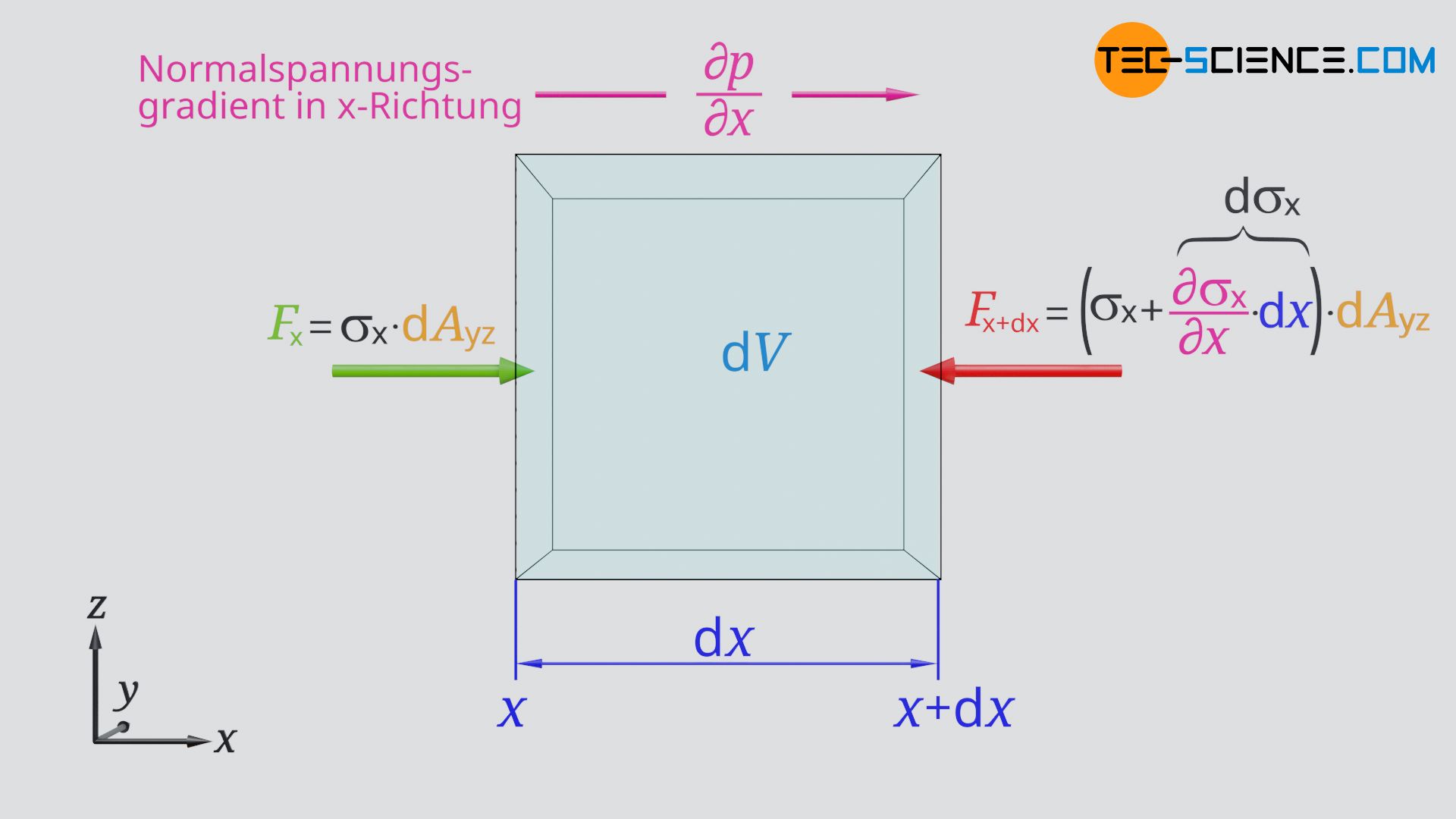
Die auf die vordere und hintere Fläche wirkenden Normalspannungen sind dabei allerdings unterschiedlich, da bspw. der Druck in Strömungsrichtung in der Regel abnimmt. Es ist also an einer betrachteten Stelle x ein Druckgradient und somit ein Spannungsgradient ∂σ_x/∂x vorhanden. Wirkt an der Stelle x die Normalspannung σ_x, dann ändert sich diese entlang der Strecke dx um ∂σ_x/∂x⋅dx. Folgende druckbedingte Normalkräfte wirken somit an der Stelle x bzw. x+dx auf das Volumenelement:

\begin{align}
& \underline{F_\text{x} = \sigma_\text{x} \cdot \text{d}A_\text{yz}} ~~~~~\text{Normalkraft an der Stelle }x\\[5px]
& \underline{F_\text{x+dx} = \left(\sigma_\text{x} + \frac{\partial \sigma_\text{x}}{\partial x}\text{d}x\right) \text{d}A_\text{yz}} ~~~~~\text{Normalkraft an der Stelle }x+\text{d}x \\[5px]
\end{align}

Da diese Kräfte offensichtlich in unterschiedliche Richtungen wirken, ergibt sich die resultierende Normalkraft F_σx auf das Volumenelement aus der Differenz beider Kräfte:

\begin{align}
\require{cancel}
& F_{\sigma_\text{x}} = F_\text{x} – F_\text{x+dx} \\[5px]
& F_{\sigma_\text{x}} = \sigma_\text{x} \cdot \text{d}A_\text{yz} – \left(\sigma_\text{x}+ \frac{\partial \sigma_\text{x}}{\partial x}\cdot \text{d}x\right) \cdot \text{d}A_\text{yz}\\[5px]
& F_{\sigma_\text{x}} = \cancel{\sigma_\text{x} \cdot \text{d}A_\text{yz}} – \cancel{\sigma_\text{x} \cdot \text{d}A_\text{yz}} – \frac{\partial \sigma_\text{x}}{\partial x} \cdot \underbrace{\text{d}x \cdot \text{d}A_\text{yz}}_{\text{d}V} \\[5px]
& \boxed{F_{\sigma_\text{x}} = ~ – \frac{\partial \sigma_\text{x}}{\partial x} \cdot \text{d}V} ~~\text{resultierende Normalkraft in x-Richtung} \\[5px]
\end{align}

Scherkräfte auf ein Volumenelement

Aufgrund der Viskosität η wirken auf die seitlichen Flächen des Fluidelements und auf die Fläche oben und unten Schubkräfte (Scherkräfte) bzw. Schubspannungen in x-Richtung. Im Gegensatz zu den zuvor betrachteten Normalspannungen, die senkrecht zur Fläche gerichtet sind, wirken die Scherspannungen parallel zur Fläche.

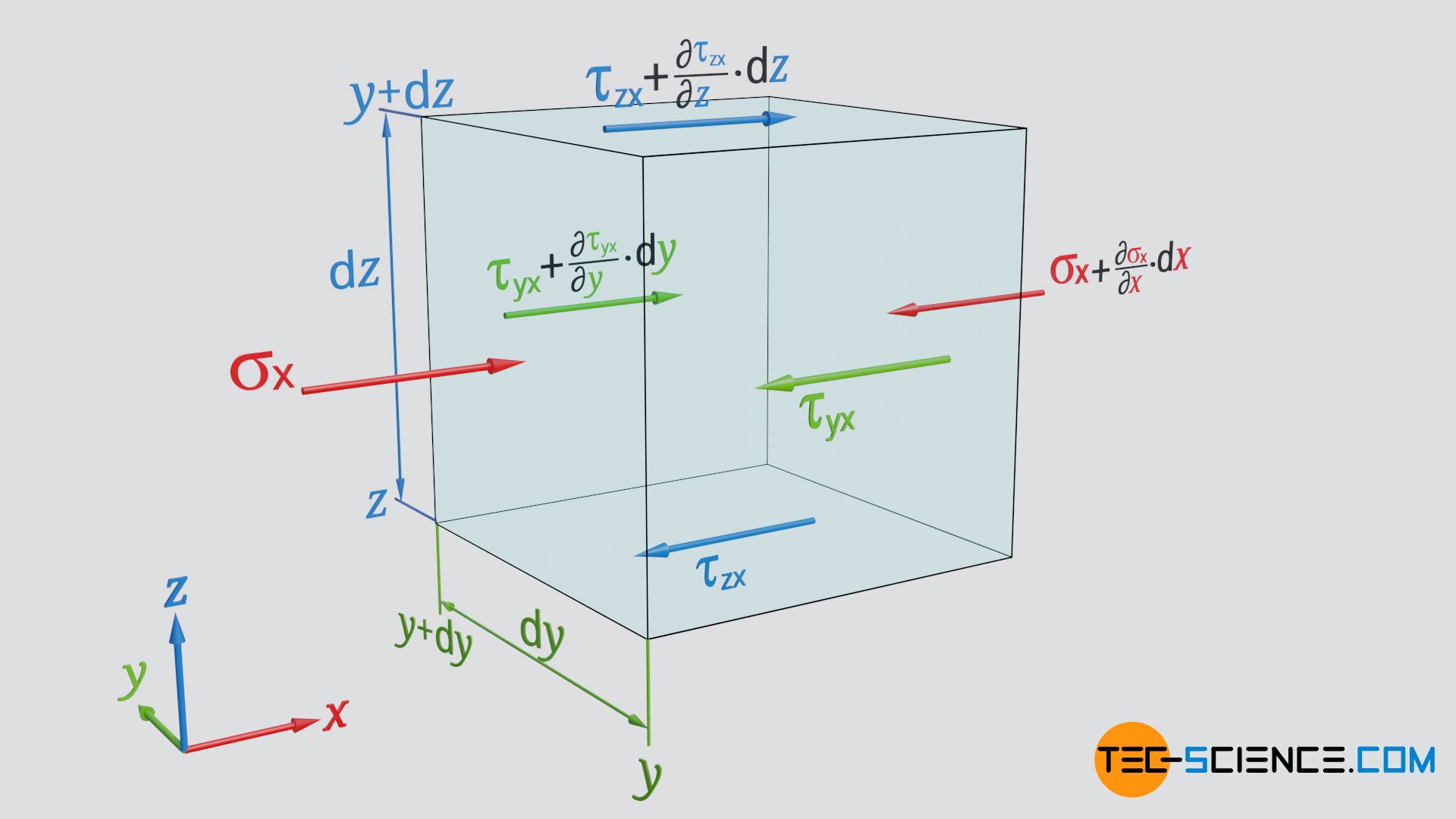
Die Schubspannungen τ_ij ermitteln sich gemäß des Newtonschen Reibungsgesetztes anhand des vorhandenen Geschwindigkeitsgradiente ∂v_j/∂i (auch Schergeschwindigkeit genannt); zur Anwendbarkeit dieses Gesetztes innerhalb eines Kontinuums später mehr:

\begin{align}
\label{newton}
& \boxed{\tau_\text{ij} = \eta \cdot \frac{\partial v_\text{j}}{\partial i}} ~~~\text{Newtonsches Reibungsgesetz}\\[5px]
\end{align}

Darin bezeichnet i (=y,z) die Richtung der Flächennormalen für die die Schubspannung ermittelt wird und j (=x) die Richtung in der die Schubspannung τ_ij letztlich wirkt. Auf diese Weise ergibt sich für die seitliche Fläche an der Position y die Bezeichnung τ_yx:

\begin{align}
&\underline{\tau_\text{yx}}~~~~~\text{Schubspannung an der Stelle }y \\[5px]
\end{align}

Über die Breite dy des Fluidelementes hinweg wird sich der Geschwindigkeitsgradient ∂v_x/∂y im Allgemeinen ändern. Somit wirkt an der Stelle y+dy eine andere Schubspannung. Man kann an dieser Stelle einen entsprechenden Schubspannungsgradienten ∂τ_yx/∂y definieren, sodass sich dann über die Länge dy folgende Schubspannung ergibt:

\begin{align}
&\underline{\tau_\text{yx}+\frac{\partial \tau_\text{yx}}{\partial y}\text{d}y}~~~~~\text{Schubspannung an der Stelle }y+\text{d}y \\[5px]
\end{align}

Konkret bedeutet ein positiver Schubspannungsgradient, dass gemäß dem Newtonschen Reibungsgesetz der Geschwindigkeitsgradient in y-Richtung ansteigt. Die Strömungsgeschwindigkeit an der Stelle y+dy ist somit größer als an der Stelle y. In Strömungsrichtung betrachtet (positive x-Richtung), strömt das Fluid rechts des Fluidelementes also langsamer vorbei und links davon schneller.

Das Fluidelement wird auf der rechten Seite sozusagen abgebremst und auf der linken Seite von der Strömung mitgerissen, d.h. beschleunigt. Die Schubspannung an der Stelle y ist somit in negative x-Richtung gerichtet und an der Stelle y+dy in positive Richtung. Die resultierende Schubspannung der beiden seitlichen Flächen ergibt sich folglich aus der Differenz beider Scherspannungen:

\begin{align}
&\tau_\text{yx,res} = \underbrace{\tau_\text{yx}+\frac{\partial \tau_\text{yx}}{\partial y}\cdot \text{d}y}_{\text{Schubspannung an der Stelle }y+\text{d}y} – \underbrace{\tau_\text{yx}}_{\text{Schubspannung an der Stelle }y} \\[5px]
&\underline{\tau_\text{yx,res}=\frac{\partial \tau_\text{yx}}{\partial y}\cdot \text{d}y}~~~~~\text{resultierende Schubspannung auf das Fluidelement} \\[5px]
\end{align}

Diese Schubspannung (Kraft pro Flächeneinheit) multipliziert mit der Fläche dA_xz ergibt schließlich die resultierende Kraft F_τyx, die auf die seitliche Flächen des Fluidelementes wirken:

\begin{align}
&F_{\tau_\text{yx}}= \tau_\text{yx,res} \cdot \text{d}A_\text{xz}\\[5px]
&F_{\tau_\text{yx}}=\frac{\partial \tau_\text{yx}}{\partial y}\cdot \underbrace{\text{d}y \cdot \text{d}A_\text{xz}}_{\text{d}V}\\[5px]
\label{for}
&\boxed{F_{\tau_\text{yx}} =\frac{\partial \tau_\text{yx}}{\partial y}\cdot \text{d}V} \\[5px]
\end{align}

Für die resultierende Schubspannung bzw. die resultierende Schubkraft F_τzx auf die obere und untere Fläche des Fluidelements gilt ganz analog:

\begin{align}
&\boxed{F_{\tau_\text{zx}} =\frac{\partial \tau_\text{zx}}{\partial z}\cdot \text{d}V} \\[5px]
\end{align}

Gewichtskraft auf ein Fluidelement

Als weitere Kraft neben Normal- und Scherkräften wirkt im Allgemeinen die Gravitation auf ein Fluidelement. Die betrachtete Strömung in x-Richtung muss dabei nicht notwendigerweise horizontal gerichtet sein, sondern kann in einem beliebigen Winkel verlaufen. In diesen Fällen ist nur diejenige Komponente der Gewichtskraft F_gx relevant, die auch in x-Richtung weist g_x bezeichnet darin die Komponente der Fallbeschleunigung in x-Richtung):

\begin{align}
&F_{\text{g}_\text{x}} = \text{d}m \cdot g_\text{x} \\[5px]
&\boxed{F_{\text{g}_\text{x}} = \rho g_\text{x} \cdot \text{d}V } ~~~\text{Gewichtskraft auf das Fluidelement in x-Richtung} \\[5px]
\end{align}

Im Gegensatz zu den Normal- oder Scherkräften, greift die Gewichtskraft nicht an Flächen an, sondern am gesamten Volumen des Fluidelements. Die Gewichtskraft zählt deshalb zu den sogenannten Volumenkräften. Auch andere angreifende Feldkräfte wie elektrische oder magnetische Kräfte zählen zu den Volumenkräften. Auch diese können am Fluidelement angreifen und müssen denn entsprechend berücksichtigt werden. An dieser Stelle soll die Gewichtskraft somit nur exemplarisch für auch andere Feldkräfte stehen.

Substantielle, lokale und konvektive Beschleunigung

Die Summe aus Normalkraft F_σx, Scherkraft F_τyx und F_τzx sowie der Volumenkraft F_gx, ergibt schließlich die insgesamt auf das Fluidelement wirkende resultierende Kraft F_xres in x-Richtung:

\begin{align}
&F_{\text{x}_\text{res}} = F_{\sigma_\text{x}} + F_{\tau_\text{yx}} + F_{\tau_\text{zx}} + F_{\text{g}_\text{x}} \\[5px]
&F_{\text{x}_\text{res}} =
– \frac{\partial \sigma_\text{x}}{\partial x} \cdot \text{d}V
+ \frac{\partial \tau_\text{yx}}{\partial y} \cdot \text{d}V
+ \frac{\partial \tau_\text{zx}}{\partial z} \cdot \text{d}V
+ \rho g_\text{x} \cdot \text{d}V
\\[5px]
\end{align}

Gemäß des zweiten Newtonschen Axioms führt diese resultierende Kraft zur folgender Beschleunigung a_x in x-Richtung, wobei dm=ϱ⋅dV die Masse des Fluidelements bezeichnet:

\begin{align}
\require{cancel}
&a_\text{x} = \frac{F_{\text{x}_\text{res}}}{\text{d}m} = \frac{F_{\text{x}_\text{res}}}{\rho~ \text{d}V} \\[5px]
&a_\text{x} =
\frac{- \frac{\partial \sigma_\text{x}}{\partial x} \cdot \cancel{\text{d}V}
+ \frac{\partial \tau_\text{yx}}{\partial y} \cancel{\text{d}V}
+ \frac{\partial \tau_\text{zx}}{\partial z} \cancel{\text{d}V}
+ \rho g_\text{x} \cdot \cancel{\text{d}V}}{\rho~ \cancel{\text{d}V}}
\\[5px]
&a_\text{x} =
\frac{- \frac{\partial \sigma_\text{x}}{\partial x}
+ \frac{\partial \tau_\text{yx}}{\partial y}
+ \frac{\partial \tau_\text{zx}}{\partial z}
+ \rho g_\text{x}}{\rho}
\\[5px]
\end{align}

und somit folgt:

\begin{align}
\label{a}
&\underline{a_\text{x}~ \rho=
– \frac{\partial \sigma_\text{x}}{\partial x}
+ \frac{\partial \tau_\text{yx}}{\partial y}
+ \frac{\partial \tau_\text{zx}}{\partial z}
+ \rho g_\text{x} }
\\[5px]
\end{align}

Die auch als substantielle Beschleunigung a_x bezeichnete Geschwindigkeitsänderung des Fluidelements in x-Richtung lässt sich zum einen durch die zeitliche Änderung der Geschwindigkeit an einem festen Ort ausdrücken (lokale Beschleunigung: ∂v_x/∂t) und zum anderen durch die Geschwindigkeitsänderung aufgrund der örtlichen Änderung des Fluidelements (konvektive Beschleunigung: ∂v_x/∂x⋅v_x + ∂v_x/∂y⋅v_y + ∂v_x/∂z⋅v_z):

\begin{align}
\label{sub}
&\underbrace{~~a_\text{x}~~}_{\text{substantielle}\\\text{Beschleunigung}} = \underbrace{\frac{\partial v_\text{x}}{\partial t}}_{\text{lokale}\\\text{Beschleunigung}} + \underbrace{\frac{\partial v_\text{x}}{\partial x}v_\text{x} + \frac{\partial v_\text{x}}{\partial y}v_\text{y} + \frac{\partial v_\text{x}}{\partial z}v_\text{z}}_\text{konvektive Beschleunigung} \\[5px]
\end{align}

Dieser Zusammenhang zwischen substantieller, lokaler und konvektiver Beschleunigung ist im Artikel Herleitung der Euler-Gleichung ausführlich hergeleitet und soll an dieser Stelle nicht weiter erläutert werden. Wird die Gleichung für die substantielle Beschleunigung (\ref{sub}) in Gleichung (\ref{a}) eingesetzt, dann folgt:

\begin{align}
\label{nav}
&\boxed{\left(\frac{\partial v_\text{x}}{\partial t} + \frac{\partial v_\text{x}}{\partial x}v_\text{x} + \frac{\partial v_\text{x}}{\partial y}v_\text{y} + \frac{\partial v_\text{x}}{\partial z}v_\text{z}\right) ~ \rho=- \frac{\partial \sigma_\text{x}}{\partial x} + \frac{\partial \tau_\text{yx}}{\partial y} + \frac{\partial \tau_\text{zx}}{\partial z} + \rho g_\text{x}} \\[5px]
\end{align}

Viskose Spannungstensor

Bei dreidimensionalen Strömung ändert sich die Geschwindigkeit bzw. der Geschwindigkeitsgradient in alle drei Richtungen. Dabei ist die entstehende Schubspannung aufgrund der Viskosität nicht mehr nur auf den Geschwindigkeitsgradient in einer bestimmten Richtung zurückzuführen, sondern noch auf einen Geschwindigkeitsgradienten senkrecht dazu.

Man diese Situation analog zur Deformation eines Fluidelementes betrachten. Man stelle sich hierzu Schubkräfte vor, die das Fluidelement verformen. Es entstehen auf diese Weise schräge Flächen, sodass die in der Fläche wirkenden Schubkräfte nun plötzlich eine weitere Raumdimension beeinflussen. Tatsächlich sind bei Fluiden die in zusätzliche Raumrichtungen wirkenden Spannungen nicht auf eine tatsächliche Deformation zurückzuführen (Stärke der Scherung), sondern auf die Scherrate (Geschwindigkeit der Scherung).

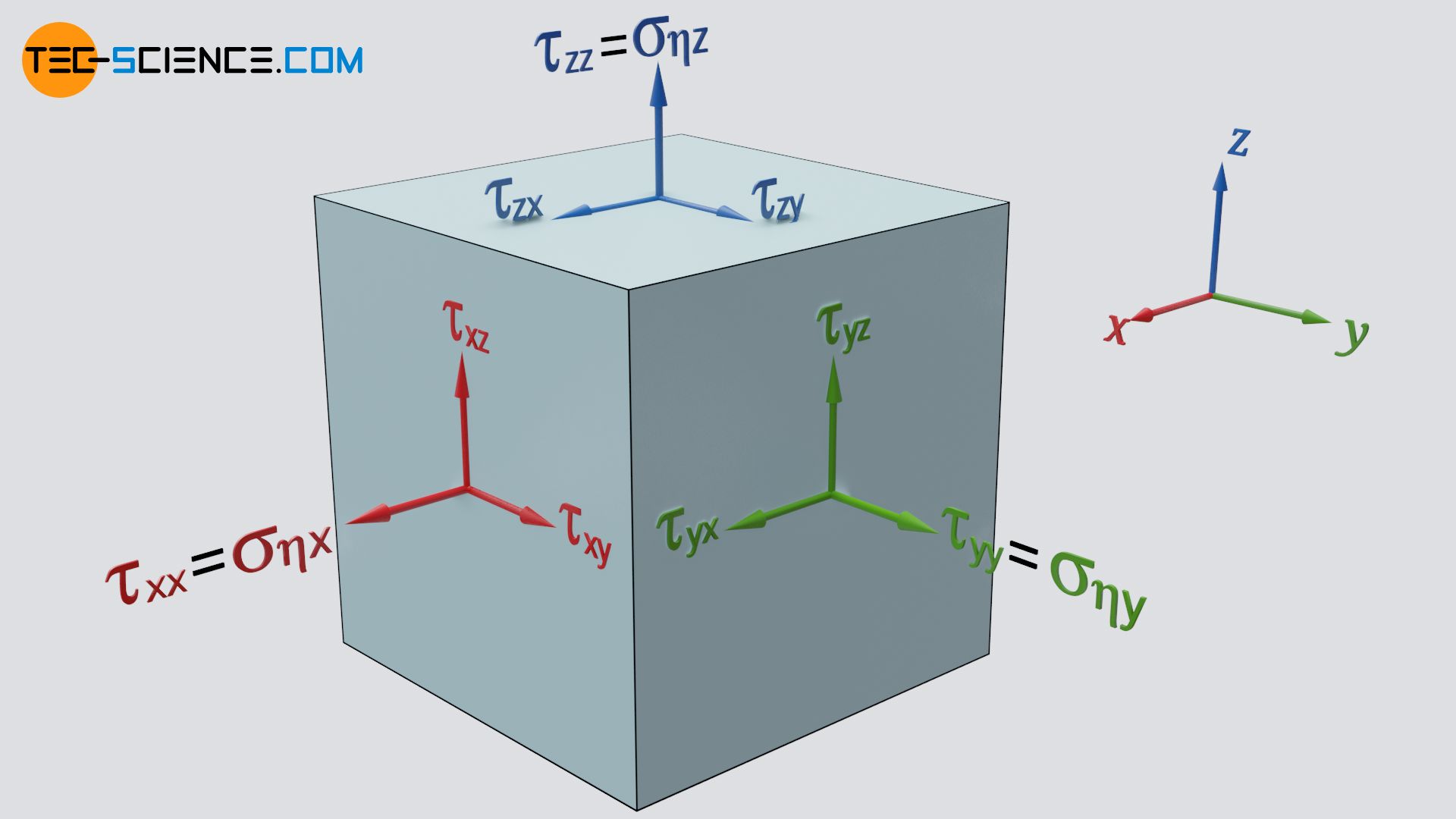
Diese Erkenntnis führt zur Einführung eines viskosen Spannungstensors, der die auf ein Fluidelement wirkenden Spannungen (Normal- und Schubspannungen) beschreibt:

\begin{align}
\label{matr1}
& \boxed{\tau =
\begin{pmatrix}
\color{red}{\tau_\text{xx}} & \tau_\text{xy} & \tau_\text{xz}
\\\
\tau_\text{yx} & \color{red}{\tau_\text{yy}} & \tau_\text{yz}
\\\
\tau_\text{zx} & \tau_\text{zy} & \color{red}{\tau_\text{zz}}
\end{pmatrix}} ~~~\text{viskoser Spannungstensor}\\[5px]
\end{align}

Für ein isotropes Newton’sches Fluid können die einzelnen Komponenten des viskosen Spannungstensors τ wie folgt anhand der Viskosität η ermittelt werden:

\begin{align}
\label{matr2}
& \boxed{\large\tau = \eta \cdot
\begin{pmatrix}
&\color{red}{\left(\frac{\partial v_\text{x}}{\partial x} + \frac{\partial v_\text{x}}{\partial x}\right)}
& \left(\frac{\partial v_\text{x}}{\partial y} + \frac{\partial v_\text{y}}{\partial x}\right)
& \left(\frac{\partial v_\text{x}}{\partial z} + \frac{\partial v_\text{z}}{\partial x}\right)
\\\
& \left(\frac{\partial v_\text{y}}{\partial x} + \frac{\partial v_\text{x}}{\partial y}\right)
&\color{red}{\left(\frac{\partial v_\text{y}}{\partial y} + \frac{\partial v_\text{y}}{\partial y}\right)}
& \left(\frac{\partial v_\text{y}}{\partial z} + \frac{\partial v_\text{z}}{\partial y}\right)
\\\
& \left(\frac{\partial v_\text{z}}{\partial x} + \frac{\partial v_\text{x}}{\partial z}\right)
& \left(\frac{\partial v_\text{z}}{\partial y} + \frac{\partial v_\text{y}}{\partial z}\right)
&\color{red}{\left(\frac{\partial v_\text{z}}{\partial z} + \frac{\partial v_\text{z}}{\partial z}\right)}
\end{pmatrix}} \\[5px]
\end{align}

Die einzelnen Einträge des Spannungstensors können auch wie folgt ermittelt werden:

\begin{align}
\label{t}
&\boxed{\tau_\text{ij} = \eta \left(\frac{\partial v_\text{i}}{\partial j} + \frac{\partial v_\text{j}}{\partial i}\right)} ~~~\text{viskose Spannung}\\[5px]
\end{align}

Es zeigt sich an dieser Stelle nun der Unterschied zum Newton’schen Reibungsansatz nach Gleichung (\ref{newton}): Bei dreidimensionalen Strömungen eines Kontinuums (Kontinuumsmechanik) hängen die Schubspannung jeweils noch von einem weiteren Geschwindigkeitsgradienten ab. Diese Erkenntnis und die Einführung des viskosen Spannungstensors ist im Wesentlichen die Leistung von Stokes.

Für die in Gleichung (\ref{nav}) enthaltenen Schubspannungen τ_yx und τ_zx gilt nach Gleichung (\ref{t}):

\begin{align}
\label{tyx}
&\underline{\tau_\text{yx} = \eta \left(\frac{\partial v_\text{y}}{\partial x} + \frac{\partial v_\text{x}}{\partial y}\right)}\\[5px]
\label{tzx}
&\underline{\tau_\text{zx} = \eta \left(\frac{\partial v_\text{z}}{\partial x} + \frac{\partial v_\text{x}}{\partial z}\right)}\\[5px]
\end{align}

Berücksichtigung der viskosen Normalspannung

Bei den angegebenen Spannungen mit identischen Indizes in Gleichung (\ref{matr1}) bzw. (\ref{matr2}) (rot markiert), zeigen offensichtlich sowohl die Flächennormale als auch die Wirkrichtung der Kraft in dieselbe Richtung. Es handelt sich dabei also nicht um Schubspannungen, sondern um Normalspannungen, die der besseren Unterscheidung deshalb häufig mit σ bezeichnet werden:

\begin{align}
& \tau_\text{xx} = \sigma_{\eta~\text{x}} \\[5px]
& \tau_\text{yy} = \sigma_{\eta~\text{y}} \\[5px]
& \tau_\text{zz} = \sigma_{\eta~\text{z}} \\[5px]
\end{align}

Dies bedeutet aber offensichtlich auch, dass die Viskosität nicht nur Schubspannungen, sondern auch Normalspannungen erzeugt. Diese aus der Viskosität resultierenden Normalspannungen sind deshalb zusätzlich mit dem Formelzeichen für die Viskosität η bezeichnet. Für die in x-Richtung wirkende viskositätsbedingte Normalspannung σ_ηx gilt nach Gleichung (\ref{t}):

\begin{align}
& \tau_\text{xx} =\underline{\sigma_{\eta~\text{x}}}= \eta \left(\frac{\partial v_\text{x}}{\partial x} + \frac{\partial v_\text{x}}{\partial x}\right) = \underline{2\eta \frac{\partial v_\text{x}}{\partial x}} \\[5px]
\end{align}

Diese viskose Normalspannung wirkt als Normalkraft zusätzlich zum (statischen) Druck in x-Richtung auf das Fluidelement. Im Gegensatz zum statischen Druck, der entgegen der Flächennormalen des Fluidelements wirkt (sozusagen auf das Fluidelement gerichtet ist), wirkt die viskose Normalspannung jedoch in Richtung der Flächennormalen (d.h. weg vom Fluidelement). Die in x-Richtung insgesamt auf das Fluidelement wirkende Normalspannung σ_x ergibt sich somit aus dem statischen Druck p, abzüglich der viskosen Normalspannung σ_ηx:

\begin{align}
& \sigma_\text{x} = p~ – \sigma_{\eta~\text{x}} \\[5px]
\label{sx}
& \underline{\sigma_\text{x} = p~ – 2\eta \frac{\partial v_\text{x}}{\partial x}} \\[5px]
\end{align}

Die Navier-Stokes-Gleichung für inkompressible Fluide

Werden die Gleichungen (\ref{tyx}), (\ref{tzx}) und (\ref{sx}) schließlich in die rechte Seite von Gleichung (\ref{nav}) eingesetzt, dann ergibt sich die nachfolgend angegebene Gleichung (der Übersichtlichkeit halber ist nur die rechte Seite der Gleichung dargestellt):

\begin{align}
&…=- \frac{\partial \sigma_\text{x}}{\partial x} + \frac{\partial \tau_\text{yx}}{\partial y} + \frac{\partial \tau_\text{zx}}{\partial z} + \rho g_\text{x} \\[5px]

&…=- \frac{\partial}{\partial x}\left(p~ – 2\eta \frac{\partial v_\text{x}}{\partial x}\right) +\eta ~\frac{\partial}{\partial y} \left(\frac{\partial v_\text{y}}{\partial x} + \frac{\partial v_\text{x}}{\partial y}\right) + \eta ~\frac{\partial}{\partial z} \left(\frac{\partial v_\text{z}}{\partial x} + \frac{\partial v_\text{x}}{\partial z}\right)+ \rho g_\text{x} \\[5px]

&…=- \frac{\partial p}{\partial x} + \color{red}{ 2\eta \frac{\partial^2 v_\text{x}}{\partial x^2}} +\eta \frac{\partial}{\partial y} \left(\frac{\partial v_\text{y}}{\partial x}\right) + \eta \frac{\partial^2 v_\text{x}}{\partial y^2}+ \eta \frac{\partial}{\partial z} \left(\frac{\partial v_\text{z}}{\partial x} \right)+ \eta \frac{\partial^2 v_\text{x}}{\partial z^2}+ \rho g_\text{x} \\[5px]
\end{align}

Den rot markierten Term können wir auch etwas anders schreiben und erhalten damit:

\begin{align}
…=&- \frac{\partial p}{\partial x} + \color{red}{\eta \frac{\partial^2 v_\text{x}}{\partial x^2} +\eta \frac{\partial}{\partial x} \left(\frac{\partial v_\text{x}}{\partial x}\right)} +\eta \frac{\partial}{\partial y} \left(\frac{\partial v_\text{y}}{\partial x}\right) + \eta \frac{\partial^2 v_\text{x}}{\partial y^2} \\[5px]&
+ \eta \frac{\partial}{\partial z} \left(\frac{\partial v_\text{z}}{\partial x} \right) + \eta \frac{\partial^2 v_\text{x}}{\partial z^2}+ \rho g_\text{x} \\[5px]
\end{align}

Wir ordnen diese Gleichung nun etwas:

\begin{align}
…=&- \frac{\partial p}{\partial x}
+ \eta \left(\frac{\partial^2 v_\text{x}}{\partial x^2}
+ \frac{\partial^2 v_\text{x}}{\partial y^2}
+ \frac{\partial^2 v_\text{x}}{\partial z^2}\right)\\[5px]&
+ \eta \frac{\partial}{\color{red}{\partial x}} \left(\frac{\partial v_\text{x}}{\color{blue}{\partial x}}\right)
+ \eta \frac{\partial}{\color{red}{\partial y}} \left(\frac{\partial v_\text{y}}{\color{blue}{\partial x}}\right)
+ \eta \frac{\partial}{\color{red}{\partial z}} \left(\frac{\partial v_\text{z}}{\color{blue}{\partial x}} \right)
+ \rho g_\text{x} \\[5px]
\end{align}

Wir können die Koordinaten nach denen wir die partielle Ableitung in den einzelnen Termen bilden auch vertauschen, denn schließlich macht es keinen Unterschied, ob wir zuerst partiell nach y ableiten und anschließend nach x oder erst nach x und anschließend nach y. Wir tauschen also die rot markierten Operatoren außerhalb der Klammer mit den blau markierten Operatoren innerhalb der Klammer:

\begin{align}
…=&- \frac{\partial p}{\partial x}
+ \eta \left(\frac{\partial^2 v_\text{x}}{\partial x^2}
+ \frac{\partial^2 v_\text{x}}{\partial y^2}
+ \frac{\partial^2 v_\text{x}}{\partial z^2}\right)\\[5px]&
+ \eta \frac{\partial}{\color{red}{\partial x}} \left(\frac{\partial v_\text{x}}{\color{blue}{\partial x}}\right)
+ \eta \frac{\partial}{\color{red}{\partial x}} \left(\frac{\partial v_\text{y}}{\color{blue}{\partial y}}\right)
+ \eta \frac{\partial}{\color{red}{\partial x}} \left(\frac{\partial v_\text{z}}{\color{blue}{\partial z}} \right)
+ \rho g_\text{x} \\[5px]
\end{align}

Wir klammern nun den Operator mit dem wir partiell nach x ableiten aus und erhalten:

\begin{align}
…=&- \frac{\partial p}{\partial x}
+ \eta \left(\frac{\partial^2 v_\text{x}}{\partial x^2}
+ \frac{\partial^2 v_\text{x}}{\partial y^2}
+ \frac{\partial^2 v_\text{x}}{\partial z^2}\right)
+ \eta \frac{\partial}{\partial x}
\color{red}{\underbrace{\left(
\frac{\partial v_\text{x}}{\partial x}
+\frac{\partial v_\text{y}}{\partial y}
+\frac{\partial v_\text{z}}{\partial z}
\right)}_{=0}}
+ \rho g_\text{x} \\[5px]
\end{align}

Der rot markierte Term ist für ein inkompressibles Fluid aufgrund der Kontinuitätsgleichung null (dies gilt in sehr guter Näherung auf für Gase bei nicht all zu großen Strömungsgeschwindigkeiten)! Diese Vereinfachung führt schließlich zur folgenden Gesamtgleichung, die die Bewegung eines in inkompressiblen Fluids als Kontinuum in x-Richtung beschreibt:

\begin{align}
&\left(\frac{\partial v_\text{x}}{\partial t}+ \frac{\partial v_\text{x}}{\partial x}v_\text{x} + \frac{\partial v_\text{x}}{\partial y}v_\text{y} + \frac{\partial v_\text{x}}{\partial z}v_\text{z}\right) \rho
=
– \frac{\partial p}{\partial x}
+ \eta \left(\frac{\partial^2 v_\text{x}}{\partial x^2}
+ \frac{\partial^2 v_\text{x}}{\partial y^2}
+ \frac{\partial^2 v_\text{x}}{\partial z^2}\right)
+ \rho g_\text{x}
\\[5px]
\end{align}

Für die Bewegung in y- und z-Richtung gelten die analogen Gleichungen. Diese Gleichungen werden schließlich als Navier-Stokes-Gleichungen bezeichnet:

\begin{align}
&\boxed{\left(\frac{\partial \color{red}{v_\text{x}}}{\partial t}
+ \frac{\partial \color{red}{v_\text{x}}}{\partial x}v_\text{x}
+ \frac{\partial \color{red}{v_\text{x}}}{\partial y}v_\text{y}
+ \frac{\partial \color{red}{v_\text{x}}}{\partial z}v_\text{z}
\right) \rho
=
– \frac{\partial p}{\partial \color{red}{x}}
+ \eta \left(\frac{\partial^2 \color{red}{v_\text{x}}}{\partial x^2}
+ \frac{\partial^2 \color{red}{v_\text{x}}}{\partial y^2}
+ \frac{\partial^2 \color{red}{v_\text{x}}}{\partial z^2}\right)
+ \rho \color{red}{g_\text{x}}}
\\[5px]

&\boxed{\left(\frac{\partial \color{green}{v_\text{y}}}{\partial t}
+ \frac{\partial \color{green}{v_\text{y}}}{\partial x}v_\text{x}
+ \frac{\partial \color{green}{v_\text{y}}}{\partial y}v_\text{y}
+ \frac{\partial \color{green}{v_\text{y}}}{\partial z}v_\text{z}
\right) \rho
=
– \frac{\partial p}{\partial \color{green}{y}}
+ \eta \left(\frac{\partial^2 \color{green}{v_\text{y}}}{\partial x^2}
+ \frac{\partial^2 \color{green}{v_\text{y}}}{\partial y^2}
+ \frac{\partial^2 \color{green}{v_\text{y}}}{\partial z^2}\right)
+ \rho \color{green}{g_\text{y}}}
\\[5px]

&\boxed{\left(\frac{\partial \color{blue}{v_\text{z}}}{\partial t}
+ \frac{\partial \color{blue}{v_\text{z}}}{\partial x}v_\text{x}
+ \frac{\partial \color{blue}{v_\text{z}}}{\partial y}v_\text{y}
+ \text{ }\frac{\partial \color{blue}{v_\text{z}}}{\partial z}v_\text{z}
\right) \rho
=
– \frac{\partial p}{\partial \color{blue}{z}}
+ \eta \left(\frac{\partial^2 \color{blue}{v_\text{z}}}{\partial x^2}
+ \text{ }\frac{\partial^2 \color{blue}{v_\text{z}}}{\partial y^2}
+ \text{ }\frac{\partial^2 \color{blue}{v_\text{z}}}{\partial z^2}\right)
+ \rho \color{blue}{g_\text{z}}}
\\[5px]
\end{align}

In vektorieller Schreibweise stellt sich die Navier-Stokes-Gleichung wie folgt dar:

\begin{align}
&\boxed{ \left[\frac{\partial \vec v}{\partial t} + \left(\vec v \cdot \vec \nabla \right) \vec v \right] \rho = – \vec \nabla p+ \eta \left( \vec \nabla^2 \vec v \right) + \rho \vec g}~~~\text{Navier-Stokes-Gleichung} \\[5px]
&\underbrace{\left[\underbrace{\frac{\partial \vec v}{\partial t}}_\text{lokale Beschl.} + \underbrace{\left(\vec v \cdot \vec \nabla \right) \vec v}_\text{konvektive Beschl.} \right]}_\text{(substantielle) Beschleunigung} \rho = \underbrace{- \vec \nabla p}_{\text{„Druckkraft“}\\\text{(Normalkraft)}}+ \underbrace{\eta \left( \vec \nabla^2 \vec v \right)}_{\text{„Reibungskraft“}\\\text{(Scherkraft)}} + \underbrace{\rho \vec g}_{\text{„Gewichtskraft“}\\\text{(Volumenkraft)}} \\[5px]
\end{align}

Beachte, dass die hier dargestellte Form der Navier-Stokes-Gleichung nur für inkompressible Fluide gilt und näherungsweise auch für relativ langsam strömende Gase!

Die Navier-Stokes-Gleichungen können im Allgemeinen nicht analytisch gelöst werden. Nur für spezielle Fälle kann unter vereinfachten Annahmen eine Lösung bzw. Näherungslösung gefunden werden. Unter anderem ergibt sich als Spezialfall von inkompressiblen Fluide in einer Rohrströmung das Gesetz von Hagen-Poiseuille. Für Fluide, bei denen die Viskosität vernachlässigt werden kann, gilt η=0 und man erhält als Spezialfall schließlich die Euler-Gleichung für reibungsfreie Strömungen:

\begin{align}
& \left[\frac{\partial \vec v}{\partial t} + \rho \left(\vec v \cdot \vec \nabla \right) \vec v \right] \rho = – \vec \nabla p+ \rho \vec g \\[5px]
&\boxed{\frac{\partial \vec v}{\partial t} + \left(\vec v \cdot \vec \nabla \right) \vec v + \frac{1}{\rho} \vec \nabla p = \vec g}~~~\text{Euler-Gleichung} \\[5px]
\end{align}