Herleitung der Euler-Gleichung (Impulserhaltung)

Die Euler-Gleichung dient der Beschreibung von reibungsfreien, instationären Strömungen mit kompressiblen und inkompressiblen Fluiden.

Komponenten der Druckkräfte am Fluidelement

Die Euler-Gleichung dient der Beschreibung von reibungsfreien (nicht-viskosen) Strömungen. Diese Gleichung beruht auf dem zweiten Newtonschen Axiom, das die Änderung der Geschwindigkeit eines Fluidteilchens auf eine Krafteinwirkung zurückführt. Damit verbunden ist letztlich auch die Impulserhaltung, sodass die Euler-Gleichung auch als Folge der Impulserhaltung angesehen werden kann.

Für die Herleitung der Euler-Gleichung betrachten wir ein infinitesimales Fluidvolumen dV mit der Masse dm. Wir beschreiben die Bewegung des Fluidelementes aus einem ortsfesten Koordinatensystem heraus (sog. Eulersche Betrachtungsweise). Das betrachtete Fluidelement bewegt sich definitionsgemäß entlang einer beliebig orientierten Stromlinie.

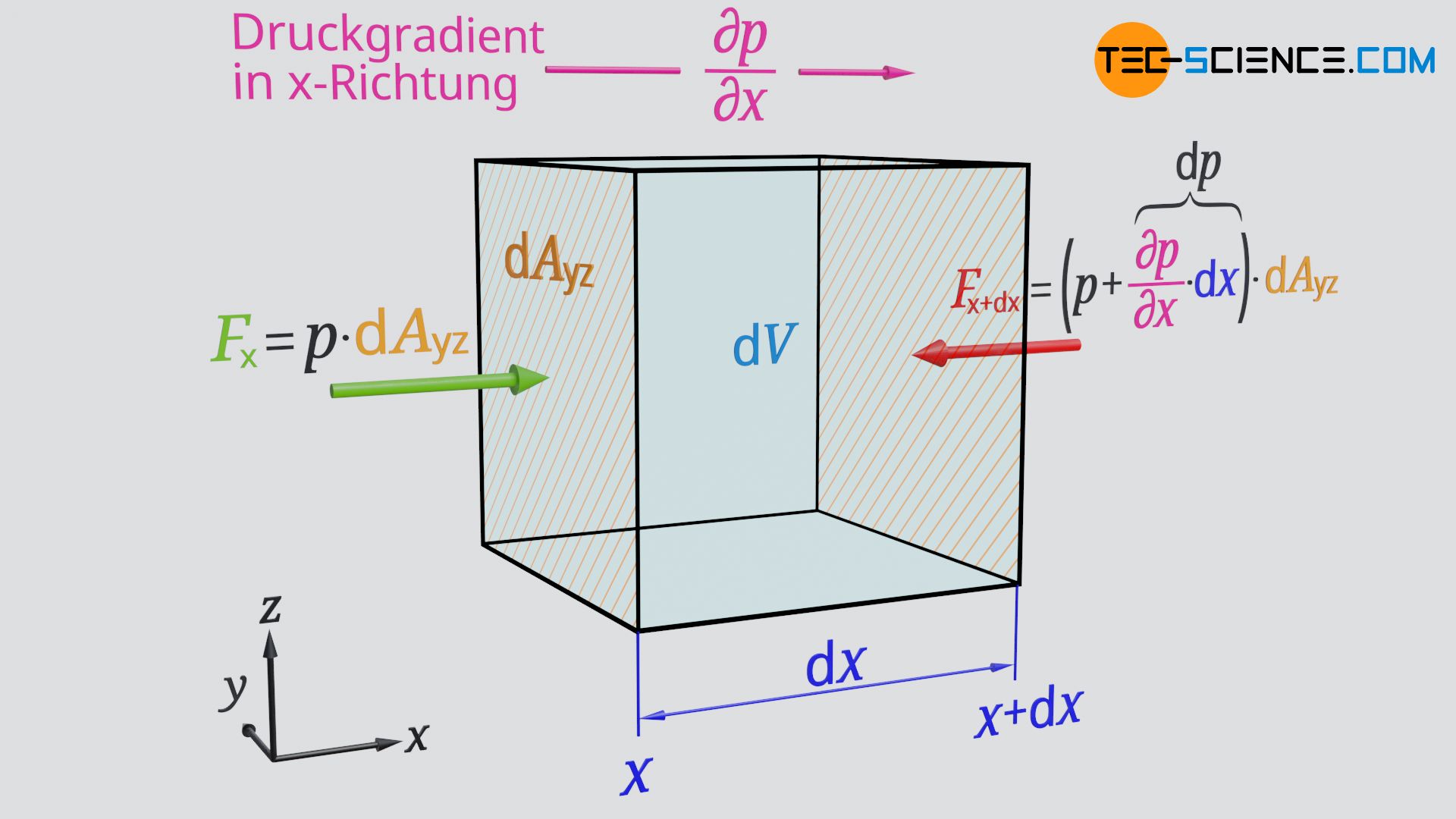
Wir betrachten zunächst die Bewegung des Fluidelementes in x-Richtung. An der Stelle x herrsche der Druck p. An dieser Stelle wirkt auf die Fläche dA_yz des Volumenelements damit folgende Kraft F_x:

\begin{align}
&\underline{F_\text{x} = p \cdot \text{d}A_\text{yz}} \\[5px]
\end{align}

Der Druck ist in einer Strömung örtlich nicht konstant. Denn Druckunterschiede sind schließlich die Ursache, dass eine Strömung überhaupt zustande kommt. Somit wird sich der Druck in x-Richtung im Allgemeinen ändern. Bei gegebenen Druckgradienten ∂p/∂x (der negativ oder positiv sein kann) ergibt sich über die Länge dx des Fluidelementes somit folgende Druckänderung dp_x:

\begin{align}
&\underline{\text{d}p_\text{x} =\frac{\partial p}{\partial x} \cdot \text{d}x} ~~~~~\text{Druckänderung entlang }\text{d}x \\[5px]
\end{align}

Diese Druckänderung führt zu folgender Kraft F_x+dx an der Stelle x+dx:

\begin{align}
&F_{\text{x+d}x}= \left(p + \text{d}p_\text{x} \right) \cdot \text{d}A_\text{yz} \\[5px]
&\underline{F_{\text{x+d}x} = \left(p + \frac{\partial p}{\partial x} \cdot \text{d}x \right) \cdot \text{d}A_\text{yz}} \\[5px]
\end{align}

Die auf die Flächen dA_yz wirkenden Kräfte F_x und F_x+dx sind jeweils entgegengesetzt gerichtet, sodass in x-Richtung folgende effektive Druckkraft F_px wirkt, die die Bewegung in x-Richtung verursacht/beeinflusst.

\begin{align}
\require{cancel}
&F_\text{px} = F_\text{x} – F_{\text{x+d}x} \\[5px]
&F_\text{px} = p \cdot \text{d}A_\text{yz} – \left(p + \frac{\partial p}{\partial x} \cdot \text{d}x \right) \cdot \text{d}A_\text{yz} \\[5px]
&F_\text{px} = \cancel{p \cdot \text{d}A_\text{yz}} – \cancel{p \cdot \text{d}A_\text{yz}} – \frac{\partial p}{\partial x} \cdot \underbrace{\text{d}x \cdot \text{d}A_\text{yz}}_{\text{d}V} \\[5px]
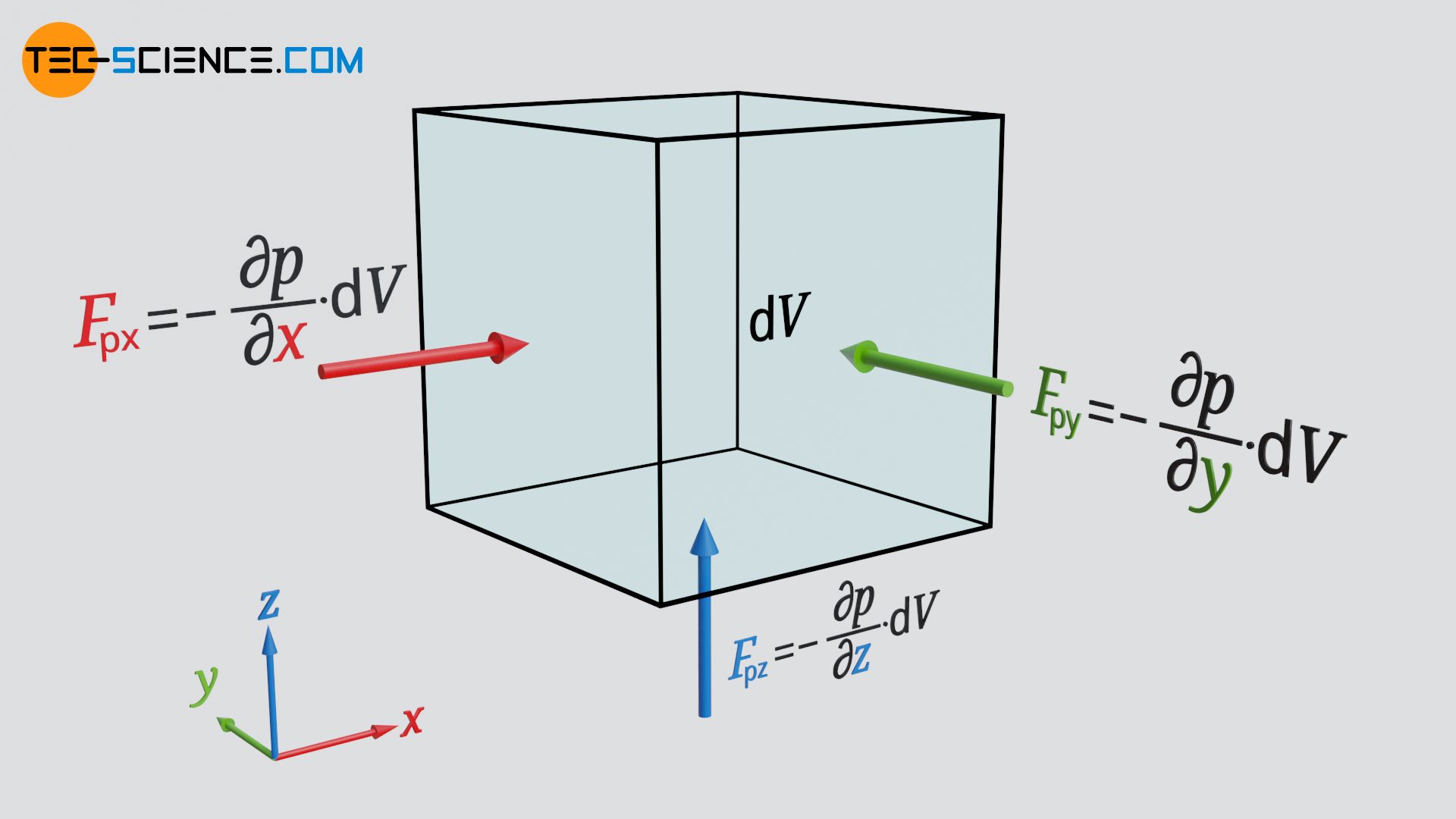
&\boxed{F_\text{px} = – \frac{\partial p}{\partial x} \cdot \text{d}V} ~~~~~\text{Betrag der Druckkraft in x-Richtung} \\[5px]
\end{align}

Das negative Vorzeichen gibt an, dass bei positivem Druckgradienten ∂p/∂x>0 die Kraft auf das Fluidelement entgegen der der positiven x-Richtung gerichtet ist, da der Druck entlang des Fluidelementes offensichtlich zunimmt. Das Fluidelement würde somit in x-Richtung abgebremst werden, sofern es sich in positive x-Richtung bewegen würde. Dieselben Überlegungen wie wir sie für die x-Richtung angestellt haben, lassen sich auch für die y-Richtung und z-Richtung anstellen. Dies führt zu analogen Gleichungen:

\begin{align}
&\boxed{F_\text{py} = – \frac{\partial p}{\partial y} \cdot \text{d}V}~~~~~\text{Betrag der Druckkraft in y-Richtung} \\[5px]
&\boxed{F_\text{pz} = – \frac{\partial p}{\partial z} \cdot \text{d}V}~~~~~\text{Betrag der Druckkraft in z-Richtung} \\[5px]
\end{align}

Darin bezeichnen ∂p/∂y und ∂p/∂z die Druckgradienten in y- bzw. z-Richtung.

Vektorschreibweise der Druckkraft

Die anhand der jeweiligen Gradienten berechneten Druckkräfte F_px, F_py und F_pz können zeilenweise als Vektor geschrieben werden. In vektorieller Schreibweise gilt für die resultierende Druckkraft F_p folglich:

\begin{align}
&\vec{F_\text{p}} = \begin{pmatrix}F_\text{px} \\\ F_\text{py} \\\ F_\text{pz} \end{pmatrix} = \begin{pmatrix}-\frac{\partial p}{\partial x}\cdot \text{d}V \\\ -\frac{\partial p}{\partial y}\cdot \text{d}V \\\ -\frac{\partial p}{\partial z} \cdot \text{d}V \end{pmatrix} = -\begin{pmatrix}\large\frac{\partial p}{\partial x} \\\ \large\frac{\partial p}{\partial y} \\\ \large\frac{\partial p}{\partial z} \end{pmatrix} \cdot \text{d}V\\[5px]
\end{align}

Der Ausdruck in der Klammer entspricht dem Druckgradienten und kann auch durch den Nabla-Operator ∇ ausgedrückt werden (häufig wird der Vektorpfeil über dem Operator auch weggelassen; formal ist der Nabla-Operator allerdings ein Vektor!):

\begin{align}
&\boxed{\vec F_\text{p} =- \vec \nabla p \cdot \text{d}V } ~~~\text{mit:}~~~\boxed{\vec \nabla =\begin{pmatrix}\large\frac{\partial}{\partial x}\\\ \large\frac{\partial }{\partial y} \\\ \large\frac{\partial}{\partial z} \end{pmatrix}} ~~~\text{Nabla-Operator}\\[5px]
& \vec \nabla p = \text{Druckgradient} \\[5px]
\end{align}

Beachte, dass die Anwendung des Nabla-Operators auf ein Skalarfeld (hier: räumliche Druckverteilung) ein Vektorfeld ergibt. Die Vektoren zeigen dabei in Richtung des stärksten Anstiegs der skalaren Größe (hier: in Richtung des größten Druckanstiegs).

Auch an dieser Stelle sei nochmals ausdrücklich darauf hingewiesen, dass das negative Vorzeichen in der oberen Formel der Tatsache gerecht wird, dass die auf ein Fluidvolumen dV wirkende Druckkraft F_p entgegen des Druckgradienten ∇p gerichtet ist. Ein Fluidelement wird somit in Richtung abnehmenden Drucks beschleunigt, sofern keine weiteren Kräfte auf das Fluidteilchen einwirken.

Scherkräfte und Feldkräfte

In einer Strömung ist die Geschwindigkeit im Allgemeinen weder zeitlich noch räumlich konstant. An den seitlichen Flächen des betrachteten Fluidvolumens strömt das Fluid somit entweder langsamer oder schneller vorbei. Es kommt zu Reibungskräften, die umso größer sind, je viskoser das Fluid ist. Da wir allerdings von einer reibungsfreien Strömung und damit von einem nicht-viskosen Fluid ausgehen, treten solche Scherkräfte in der Strömung nicht auf.

Weitere Kräfte, die am Fluid angreifen, aber im Allgemeinen nicht vernachlässigt werden können, sind Feldkräfte wie bspw. durch die Gravitation verursacht. Luftströmung auf der Erde oder Flüssigkeitsströmungen in Rohren werden bspw. maßgeblich durch die Gravitation beeinflusst. Bei Strömungen die zum Beispiel ferromagnetische Fluidpartikel enthalten, beeinflusst auch ein äußeres Magnetfeld die Strömung.

Auch elektrisch geladene Partikel in einem Fluid sind denkbar, sodass die Strömung dann durch ein äußeres elektrisches Feld beeinflusst wird. Wasser wird bereits aufgrund der Dipolwechselwirkung der H₂O-Moleküle in einem elektrischen Feld beeinflusst, ohne dass dabei elektrisch geladene Partikel enthalten sein müssen. Dies lässt sich mit einem elektrisch aufgeladenen Plastikstab eindrucksvoll demonstrieren. Bringt man den geladenen Plastikstab in die Nähe eines dünnen Wasserstrahls, dann stellt man fest, dass der Strahl abgelenkt wird.

Auf ein Fluidelement wirken neben der Druckkraft F_p somit auch Feldkräfte F_G (die Gewichtskraft soll an dieser Stelle nur stellvertretend für auch andere mögliche Feldkräfte stehen!). Die Summe beider Kräfte entspricht dann letztlich der resultierenden beschleunigenden Kraft F_b, die die Bewegung des Fluidelementes beeinflusst:

\begin{align}
& \vec{F}_\text{b} = \vec F_\text{G}+ \vec F_\text{p}\\[5px]
\label{besch}
&\boxed{\vec{F}_\text{b} = \vec F_\text{G}- \vec \nabla p \cdot \text{d}V } ~~~~~\text{beschleunigende Kraft auf ein Fluidelement}\\[5px]
\end{align}

Zweites Newtonsches Axiom (substantielle Beschleunigung)

Gemäß des zweiten Newtonschen Axioms führt die beschleunigende Kraft F_b zu einer entsprechenden Geschwindigkeitsänderung (Beschleunigung), die von der Masse dm des betrachteten Fluidelements abhängt. Diese materielle Beschleunigung wird auch als totale oder substantielle Beschleunigung a_sub bezeichnet:

\begin{align}
& \boxed{\vec a_\text{sub} = \frac{\vec F_\text{b}}{\text{d}m}} ~~~~~\text{2. Newtonsches Axiom}\\[5px]
& \vec a_\text{sub} = \frac{\vec F_\text{G}- \vec \nabla p \cdot \text{d}V}{\text{d}m} \\[5px]
& \vec a_\text{sub} = \frac{\vec F_\text{G}}{\text{d}m}- \frac{\vec \nabla p \cdot \text{d}V}{\text{d}m}
~~~\text{mit} ~~~\text{d}m=\rho \cdot \text{d}V ~~~\text{folgt:}\\[5px]
& \vec a_\text{sub} = \underbrace{\frac{\vec F_\text{G}}{\text{d}m}}_{\text{spezifische Feldkraft } g}- \frac{\vec \nabla p \cdot \text{d}V}{\rho \cdot \text{d}V} \\[5px]
\label{eu}
& \boxed{\vec a_\text{sub} = \vec g- \frac{1}{\rho} \vec \nabla p} ~~~~~\text{substantielle Beschleunigung}\\[5px]
\end{align}

Der Quotient von Feldkraft F_G und Masse dm lässt sich allgemein als Feldkraft pro Masseneinheit auffassen und entspricht im Falle der Gewichtskraft gerade der Fallbeschleunigung g. Sollten noch andere Feldkräfte wie magnetische oder elektrische Kräfte angreifen, so sind diese ebenfalls als massenspezifische Feldkräfte in der Gleichung zu berücksichtigen.

Lokale und konvektive Beschleunigung

Die substantielle Beschleunigung, d.h. die tatsächlich beobachtbare Beschleunigung eines materiellen Fluidelements (deshalb auch als materielle Beschleunigung bezeichnet), lässt sich letztlich auf zwei Ursachen zurückführen. Zum einen ändert sich eine Strömung und damit die Geschwindigkeit eines Fluidelementes nämlich nicht nur zeitlich, sondern auch örtlich. Die substantielle Beschleunigung ist somit auf eine zeitliche Komponente (lokale Beschleunigung) und eine örtliche Komponente (konvektive Beschleunigung) zurückzuführen.

Wir können uns hierzu eine Luftströmung an einem windigen Tag vorstellen. Der Wind weht dabei mit einer sich ständig ändernden Richtung (instationäre Strömung). Ein Fluidelement an einem bestimmten Ort betrachtet, ändert also von einer Sekunde auf die nächste seine Geschwindigkeit. Dies ist eine Folge der sich zeitlich permanent ändernden Strömung. Die darauf zurückzuführende Beschleunigung wird deshalb auch als lokale Beschleunigung a_lok bezeichnet, da sie eine Folge der sich ändernden Geschwindigkeit an einem festen (lokalen) Ort ist.

Man könnten nun schlussfolgern, dass bei einer stationären Strömung, bei der sich die Geschwindigkeit zeitlich nicht ändert, folglich keine Beschleunigung auf die Fluidteilchen wirke. Dem ist allerdings nicht so. Die Geschwindigkeit ändert sich bei einer stationären Strömung zwar zeitlich an einem festen Ort nicht mehr, aber ein Fluidteilchen muss beim Strömen im Allgemeinen dennoch seine Geschwindigkeit permanent ändern. Zum Beispiel ist die Strömungsgeschwindigkeit in einem Rohr an einer Engstelle größer im Vergleich zu einem Punkt in einem größeren Strömungsquerschnitt. Ein Fluidteilchen wird trotz der fehlenden zeitlichen Änderung der Strömung im Allgemeinen also dennoch beschleunigt, wenn es einen Ort ändert.

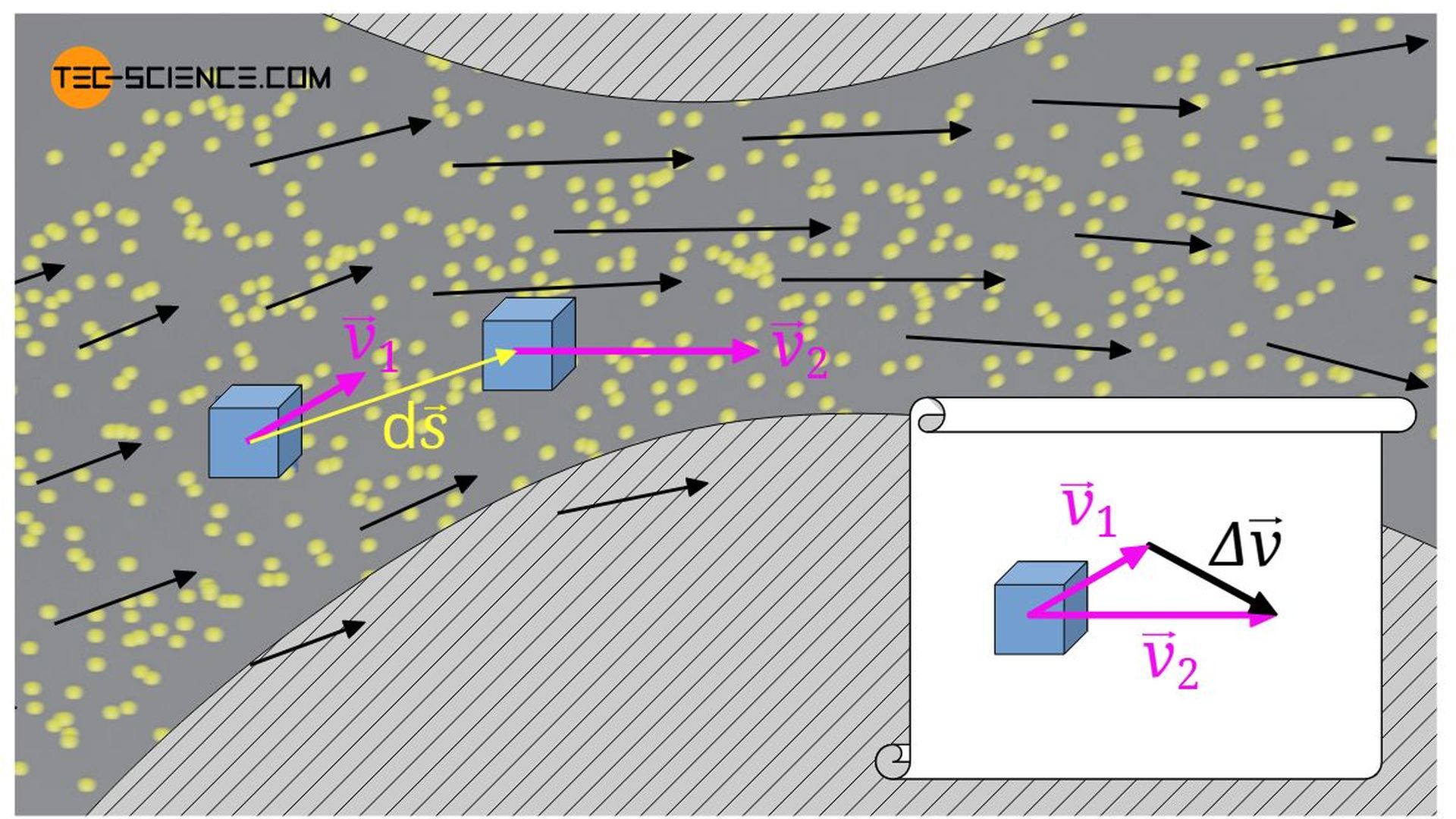
Auch das Strömen von Wind um eine gebogene Strecke erfordert ständig eine Anpassung des strömenden Fluidteilchens an die neue Geschwindigkeitsrichtung und damit eine Beschleunigung. Die auf die Änderung des Ortes zurückzuführende Beschleunigung wird deshalb auch als konvektive Beschleunigung a_kon bezeichnet.

Zusammenfassend lässt sich also festhalten:

• Die lokale Beschleunigung ist auf die sich zeitlich ändernde Strömungsgeschwindigkeit einer instationären Strömung an einem festen Ort zurückzuführen.
• Die konvektive Beschleunigung ist auf die sich von Ort zu Ort ändernde Strömungsgeschwindigkeit zurückzuführen.
• Beide Beschleunigungsanteile zusammen ergeben die beobachtbare Beschleunigung, die auch als substantielle oder materielle Beschleunigung bezeichnet wird.

Beachte, dass der lokale Anteil der Beschleunigung bei einer stationären Strömung entfällt, da sich die Geschwindigkeit an einem festen Ort der Strömung dann zeitlich nicht ändert!

Zusammenhang zwischen lokaler, konvektiver und substantieller Beschleunigung

Wir betrachten der Einfachheit halber zunächst ein Fluidteilchen auf einer Stromline s und beschreiben die Bewegung auf dieser Stromlinie (eindimensionale Bewegung). Die substantielle Änderung der Geschwindigkeit dv, d.h. die tatsächlich beobachtbare Geschwindigkeitsänderung, erhält man in diesem Fall also über die zeitliche Änderung der Geschwindigkeit ∂v/∂t innerhalb der Zeit dt (lokaler Anteil) und über eine räumliche Änderung der Geschwindigkeit ∂v/∂s (Gradient) innerhalb der Strecke ds (konvektiver Anteil):

\begin{align}
&\underbrace{\text{d}v}_{\text{substantielle Änderung}} = \underbrace{\frac{\partial v}{\partial t} \text{d}t}_{\text{lokale Änderung}} + \underbrace{\frac{\partial v}{\partial s} \text{d} s}_{\text{konvektive Änderung}}\\[5px]
\end{align}

Teilt man die obere Gleichung durch die Zeitdauer dt, so erhält man folgenden Ausdruck für die substantielle Beschleunigung a_sub in tangentialer Richtung der Stromlinie:

\begin{align}
\require{cancel}
&\boxed{a_\text{sub} = \frac{\text{d}v}{\text{d}t}} = \frac{\partial v}{\partial t} \frac{\cancel{\text{d}t}}{\cancel{\text{d}t}}+ \frac{\partial v}{\partial s} \underbrace{\frac{\text{d}s}{\text{d}t}}_{v} \\[5px]
&a_\text{sub} = \underbrace{~~~~~\frac{\partial v}{\partial t}~~~~~}_{\text{lokale Beschleunigung}} + \underbrace{~~~~~\frac{\partial v}{\partial s}v~~~~~}_{\text{konvektive Beschleunigung}} \\[5px]
\end{align}

\begin{align}
& \boxed{a_\text{sub} = \frac{\partial v}{\partial t} + \frac{\partial v}{\partial s}v} &&\text{substantielle Beschleunigung}\\[5px]
& \boxed{a_\text{lok}=\frac{\partial v}{\partial t}} &&\text{lokale Beschleunigung} \\[5px]
& \boxed{a_\text{kon}= \frac{\partial v}{\partial s}v} &&\text{konvektive Beschleunigung} \\[5px]
\end{align}

Der Term der konvektiven Beschleunigung ist offensichtlich von der Strömungsgeschwindigkeit abhängt. Dies wird auch anschaulich klar, denn strömt das Fluidelement sehr schnell, dann legt dieses innerhalb einer bestimmten Zeit eine relativ große Strecke zurück. Bei gegebenem Geschwindigkeitsgradienten ∂c/∂s bedeutet dies dann auch eine entsprechend große Änderung der Geschwindigkeit und somit eine große Beschleunigung.

Substantielle Beschleunigung als Vektor

Die Beschreibung der Bewegung beschränkte sich der Einfachheit halber bisher auf die eindimensionale Bewegung eines Fluidteilchens auf einer Stromlinie. Im dreidimensionalen Fall, d.h. bei der Beschreibung der Bewegung aus einem ortsfesten Koordinatensystem heraus, lässt sich der lokale Beschleunigungsanteil ebenfalls noch relativ einfach in Vektorform schreiben:

\begin{align}
& \boxed{\vec a_\text{lok}=\frac{\partial \vec v}{\partial t} = \begin{pmatrix}\Large\frac{\partial v_x}{\partial t} \\\ \Large\frac{\partial v_y}{\partial t} \\\ \Large\frac{\partial v_z}{\partial t} \end{pmatrix} } ~~~~~\text{lokale Beschleunigung} \\[5px]
\end{align}

Im Gegensatz hierzu ist die Beschreibung der konvektiven Beschleunigung deutlich komplizierter, da es sich dabei um eine Ortsabhängigkeit in drei Dimensionen handelt. Jede Geschwindigkeitskomponente ändert sich nicht nur aufgrund einer lokalen Ortsänderung in einer Dimension, sondern ist die Folge einer Ortsänderung in allen drei Raumdimensionen!

Die Geschwindigkeitskomponente in x-Richtung wird sich im Allgemeinen nämlich nicht nur dann ändern, wenn sich ein Fluidteilchen in x-Richtung bewegt. Die Geschwindigkeit in x-Richtung wird sich zum Beispiel auch dann ändern, wenn sich das Fluidteilchen in y-Richtung bewegt, weil dort bspw. die Strömungsgeschwindigkeit in x-Richtung geringer ist. Auch eine Ortsänderung in z-Richtung hat im Allgemeinen eine Änderung der Geschwindigkeit in x-Richtung zur Folge, weil dort bspw. die Strömungsgeschwindigkeit in x-Richtung größer wird.

Die konvektive Beschleunigungskomponente in x-Richtung (a_kon,x) ist somit auf die Ortsänderung in alle drei Raumdimensionen zurückzuführen:

\begin{align}
& \underline{a_\text{kon,x}=\frac{\partial v_\text{x}}{\partial x}v_\text{x} + \frac{\partial v_\text{x}}{\partial y}v_\text{y} + \frac{\partial v_\text{x}}{\partial z}v_\text{z}} ~~~~~\text{konvektive Beschleunigung in }x\text{-Richtung} \\[5px]
\end{align}

Nochmals zur Erläuterung: Die Geschwindigkeit eines Fluidteilchens in x-Richtung wird sich im Allgemeinen eben nicht nur bei einer Ortsänderung in x-Richtung ändern (Geschwindigkeitsgradient ∂v_x/∂x), sondern auch bei einer Ortsänderung in y-Richtung (Geschwindigkeitsgradient ∂v_x/∂y) oder z-Richtung (Geschwindigkeitsgradient ∂v_x/∂z).

Für die konvektiven Beschleunigungskomponenten in y- und z-Richtung gelten die analogen Überlegungen:

\begin{align}
& \underline{a_\text{kon,y}=\frac{\partial v_\text{y}}{\partial x}v_\text{x} + \frac{\partial v_\text{y}}{\partial y}v_\text{y} + \frac{\partial v_\text{y}}{\partial z}v_\text{z}} ~~~~~\text{konvektive Beschleunigung in }y\text{-Richtung} \\[5px]
& \underline{a_\text{kon,y}=\frac{\partial v_\text{z}}{\partial x}v_\text{x} + \frac{\partial v_\text{z}}{\partial y}v_\text{y} + \frac{\partial v_\text{z}}{\partial z}v_\text{z}} ~~~~~\text{konvektive Beschleunigung in }z\text{-Richtung} \\[5px]
\end{align}

Der Vektor der konvektiven Beschleunigung a_kon stellt sich insgesamt also mit 9 Termen dar:

\begin{align}
& \boxed{\vec a_\text{kon}= \large \begin{pmatrix} a_\text{kon,x}\\\ a_\text{kon,y}\\\ a_\text{kon,z} \end{pmatrix} 
= \Large \begin{pmatrix}
\frac{\partial v_\text{x}}{\partial x}v_\text{x} + \frac{\partial v_\text{x}}{\partial y}v_\text{y} + \frac{\partial v_\text{x}}{\partial z}v_\text{z}
\\\
\frac{\partial v_\text{y}}{\partial x}v_\text{x} + \frac{\partial v_\text{y}}{\partial y}v_\text{y} + \frac{\partial v_\text{y}}{\partial z}v_\text{z}
\\\
\frac{\partial v_\text{z}}{\partial x}v_\text{x} + \frac{\partial v_\text{z}}{\partial y}v_\text{y} + \frac{\partial v_\text{z}}{\partial z}v_\text{z}
\end{pmatrix} 
} \\[0px]
&\text{konvektive Beschleunigung} \\[5px]
\end{align}

Die konvektive Beschleunigung lässt sich mit Hilfe des Nabla-Operators ∇ deutlich kompakter darstellen:

\begin{align}
& \boxed{\vec a_\text{kon} = \left(\vec v \cdot \vec \nabla \right) \vec v}~~~\text{konvektive Beschleunigung} \\[5px]
\end{align}

Für den Vektor der substantielle Beschleunigung a_sub, als Summe von lokaler und konvektiver Beschleunigung, gilt somit:

\begin{align}
\label{en}
&\boxed{\vec a_\text{sub} = \frac{\partial \vec v}{\partial t} + \left(\vec v \cdot \vec \nabla \right) \vec v} ~\text{substantielle Beschleunigung} \\[5px]
& \boxed{\vec a_\text{sub}
= \Large \begin{pmatrix}
\frac{\partial v_x}{\partial t} + \frac{\partial v_\text{x}}{\partial x}v_\text{x} + \frac{\partial v_\text{x}}{\partial y}v_\text{y} + \frac{\partial v_\text{x}}{\partial z}v_\text{z}
\\\
\frac{\partial v_y}{\partial t} + \frac{\partial v_\text{y}}{\partial x}v_\text{x} + \frac{\partial v_\text{y}}{\partial y}v_\text{y} + \frac{\partial v_\text{y}}{\partial z}v_\text{z}
\\\
\frac{\partial v_z}{\partial t} + \frac{\partial v_\text{z}}{\partial x}v_\text{x} + \frac{\partial v_\text{z}}{\partial y}v_\text{y} + \frac{\partial v_\text{z}}{\partial z}v_\text{z}
\end{pmatrix} \\[5px]
}
\end{align}

Setzt man Gleichung (\ref{en}) in Gleichung (\ref{eu}) ein, dann erhält man letztlich die Bewegungsgleichung eines Fluidteilchens in einer reibungsfreien, instationären Strömung. Diese Gleichung wird auch als Euler-Gleichung bezeichnet und gilt sowohl für inkompressible als auch für kompressible Fluide:

\begin{align}
& \vec a_\text{sub} = \vec g- \frac{1}{\rho} \vec \nabla p \\[5px]
&\frac{\partial \vec v}{\partial t} + \left(\vec v \cdot \vec \nabla \right) \vec v = \vec g- \frac{1}{\rho} \vec \nabla p \\[5px]
&\boxed{\frac{\partial \vec v}{\partial t} + \left(\vec v \cdot \vec \nabla \right) \vec v + \frac{1}{\rho} \vec \nabla p = \vec g}~~~\text{Euler-Gleichung} \\[5px]
\end{align}

Die Euler-Gleichung kann auch in Komponenten angegeben werden:

\begin{align}
& \boxed{\frac{\partial v_\text{x}}{\partial t} + \frac{\partial v_\text{x}}{\partial x}v_\text{x} + \frac{\partial v_\text{x}}{\partial y}v_\text{y} + \frac{\partial v_\text{x}}{\partial z}v_\text{z} + \frac{1}{\rho} \frac{\partial p}{\partial x} = g_\text{x}}~~~\text{Euler-Gln. in x-Richung} \\[5px]
& \boxed{\frac{\partial v_\text{y}}{\partial t} + \frac{\partial v_\text{y}}{\partial x}v_\text{x} + \frac{\partial v_\text{y}}{\partial y}v_\text{y} + \frac{\partial v_\text{y}}{\partial z}v_\text{z} + \frac{1}{\rho} \frac{\partial p}{\partial y} = g_\text{y}}~~~\text{Euler-Gln. in y-Richung} \\[5px]
& \boxed{\frac{\partial v_\text{z}}{\partial t} + \frac{\partial v_\text{z}}{\partial x}v_\text{x} + \frac{\partial v_\text{z}}{\partial y}v_\text{y} + \frac{\partial v_\text{z}}{\partial z}v_\text{z} + \frac{1}{\rho} \frac{\partial p}{\partial z} = g_\text{z}}~~~\text{Euler-Gln. in z-Richung} \\[5px]
\end{align}

Beachte bei der Berechnung der konvektiven Beschleunigung mithilfe des Nabla-Operators folgende Vorgehensweise:

\begin{align}
\vec a_\text{kon} &= \left(\vec v \cdot \vec \nabla \right) \vec v\\[5px]
&= \left[\begin{pmatrix} v_x \\\ v_y \\\ v_z \end{pmatrix}
\cdot \begin{pmatrix} \frac{\partial}{\partial x} \\\ \frac{\partial}{\partial y} \\\ \frac{\partial}{\partial z} \end{pmatrix} \right] \cdot \begin{pmatrix} v_x \\\ v_y \\\ v_z \end{pmatrix}\\[5px]
&=\left[ v_x \frac{\partial}{\partial x} + v_y \frac{\partial}{\partial y} + v_z \frac{\partial}{\partial z} \right] \cdot \begin{pmatrix} v_x \\\ v_y \\\ v_z \end{pmatrix}\\[5px]
&=\Large \begin{pmatrix}
v_\text{x} \frac{\partial v_\text{x}}{\partial x} + v_\text{y} \frac{\partial v_\text{x}}{\partial y} +v_\text{z} \frac{\partial v_\text{x}}{\partial z}
\\\
v_\text{x} \frac{\partial v_\text{y}}{\partial x} + v_\text{y} \frac{\partial v_\text{y}}{\partial y} +v_\text{z} \frac{\partial v_\text{y}}{\partial z}
\\\
v_\text{x} \frac{\partial v_\text{z}}{\partial x} +v_\text{y} \frac{\partial v_\text{z}}{\partial y} +v_\text{z} \frac{\partial v_\text{z}}{\partial z}
\end{pmatrix} 
\end{align}

Anwendung der Euler-Gleichung entlang einer Stromlinie (Bernoulli-Gleichung)

Wir möchten an dieser Stelle die Euler-Gleichung auf eine Stromlinie anwenden und die Zustandsänderung einer Strömung entlang dieser Stromline beschreiben. In diesem Fall haben wir es mit einer eindimensionaler Beschreibung zu tun. Die Geschwindigkeit v entspricht der ortsabhängigen Geschwindigkeit auf der Stromlinie und p dem ebenfalls ortsabhängigen Druck. Mit s als Ortskoordinate entlang der Stromlinie lautet die Euler-Gleichung wie folgt:

\begin{align}
&\frac{\partial v}{\partial t} + \frac{\partial v}{\partial s}v + \frac{1}{\rho} \frac{\partial p}{\partial s} = – g \cdot \cos(\alpha) \\[5px]
\end{align}

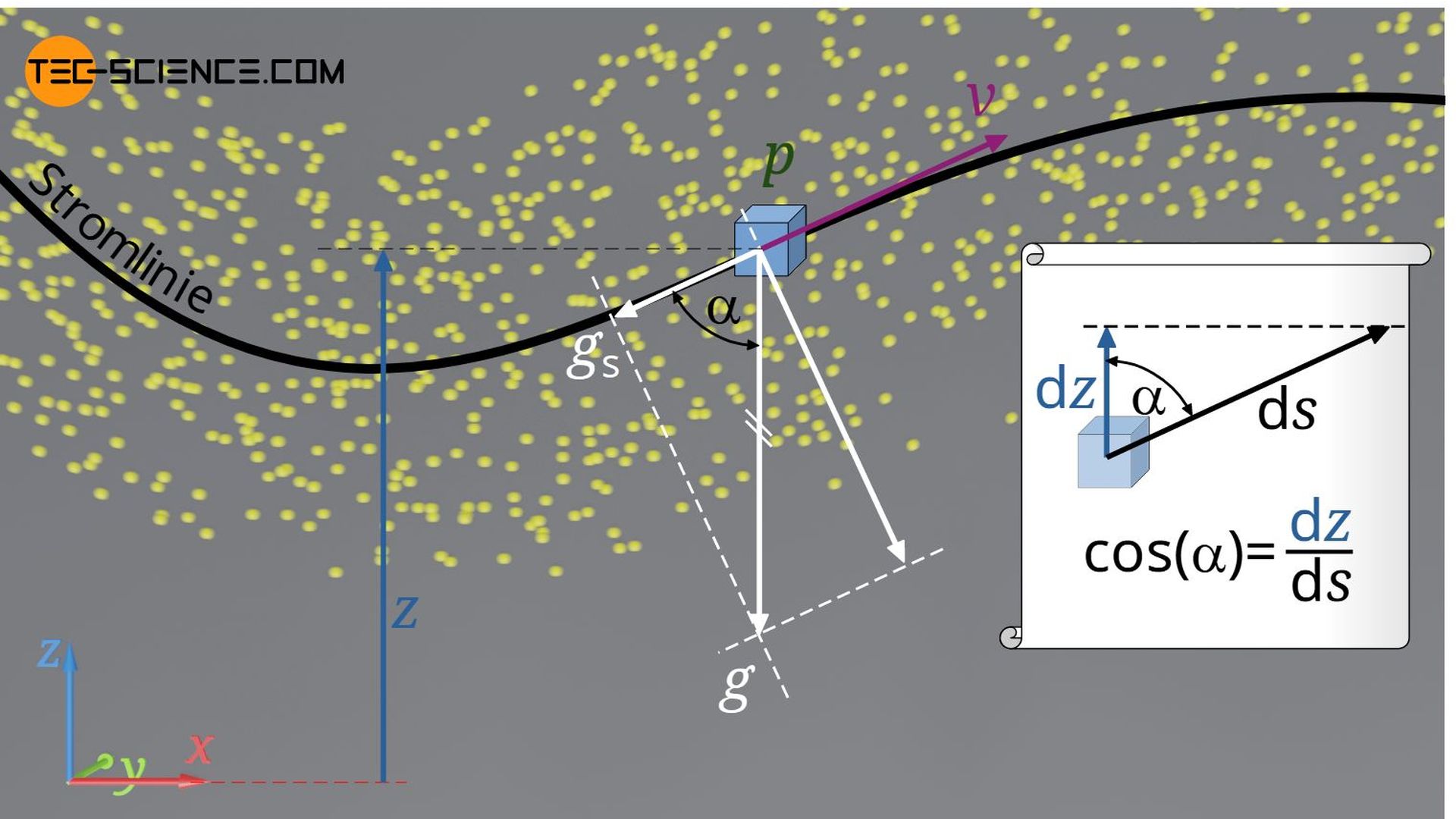
Der Winkel α entspricht dem Winkel zwischen der senkrechten z-Richtung und der Tangente der Stromlinie s. Der Term -g⋅cos(α) beschreibt damit die entgegen der Stromlinie wirkende Komponente der Fallbeschleunigung, die bei einem positiven Winkel α zu einer abbremsenden Kraft des Fluidteilchen führt (deshalb das negative Vorzeichen). Eine infinitesimale Änderung auf der Stromlinie ds hängt über den Winkel α wie folgt mit der infinitesimalen Änderung dz in z-Richtung zusammen:

\begin{align}
&\cos(\alpha) = \frac{\text{d}z}{\text{d}s}\\[5px]
\end{align}

Damit gilt für die Euler-Gleichung entlang der Stromlinie:

\begin{align}
&\frac{\partial v}{\partial t} + \frac{\partial v}{\partial s}v + \frac{1}{\rho} \frac{\partial p}{\partial s} = – g \frac{\text{d}z}{\text{d}s}\\[5px]
\end{align}

Der Einfachheit halber gehen wir im Folgenden davon aus, dass die Strömung stationär sei und das betrachtete Fluid inkompressibel. In diesem Fall ist die Geschwindigkeit keine Funktion der Zeit und damit die partielle Ableitung der Geschwindigkeit nach der Zeit Null (∂v/∂t=0). Aufgrund der Inkompressibilität ist zudem die Dichte keine Funktion des Ortes. Anstelle der partiellen Ableitungen nach dem Ort, können wir nun auch die totalen Differentiale schreiben. Wir erhalten dann folgenden Zusammenhang zwischen den infinitesimalen Änderungen von Druck, Geschwindigkeit und Höhe entlang der Stromlinie:

\begin{align}
\require{cancel}
&\cancel{\frac{\partial v}{\partial t}} + \frac{\text{d}v}{\text{d}s}v + \frac{1}{\rho} \frac{\text{d}p}{\text{d}s} = -g \frac{\text{d}z}{\text{d}s}\\[5px]
&\frac{\text{d} v}{\text{d}s}v + \frac{1}{\rho} \frac{\text{d}p}{\text{d}s} = -g \frac{\text{d}z}{\text{d}s}&&|\cdot \text{d}s\\[5px]
&v~\text{d}v + \frac{1}{\rho} \text{d}p = -g \text{d}z&&|\cdot \rho\\[5px]
&\underline{\text{d}p + \rho v ~\text{d}v ~ + \rho g ~\text{d}z = 0}\\[5px]
\end{align}

Diese Gleichung beschreibt den Zusammenhang zwischen den infinitesimalen Änderungen von Druck, Geschwindigkeit und Höhe entlang einer Stromlinie. Wir können diese Gleichung nun integrieren, um nicht mehr die Zusammenhänge zwischen den Änderungen der Größen, sondern die Zusammenhänge zwischen den Größen selbst zu erhalten. Die als konstant betrachtete Dichte und die Fallbeschleunigung können dabei vor das Integral geschrieben werden können.

\begin{align}
&\int \left(\text{d}p + \rho v ~\text{d}v ~ + \rho g ~ \text{d}z \right)= \text{konstant}\\[5px]
&\int \text{d}p + \rho \int v ~\text{d}v ~ + \rho g ~\int \text{d}z = \text{konstant}\\[5px]
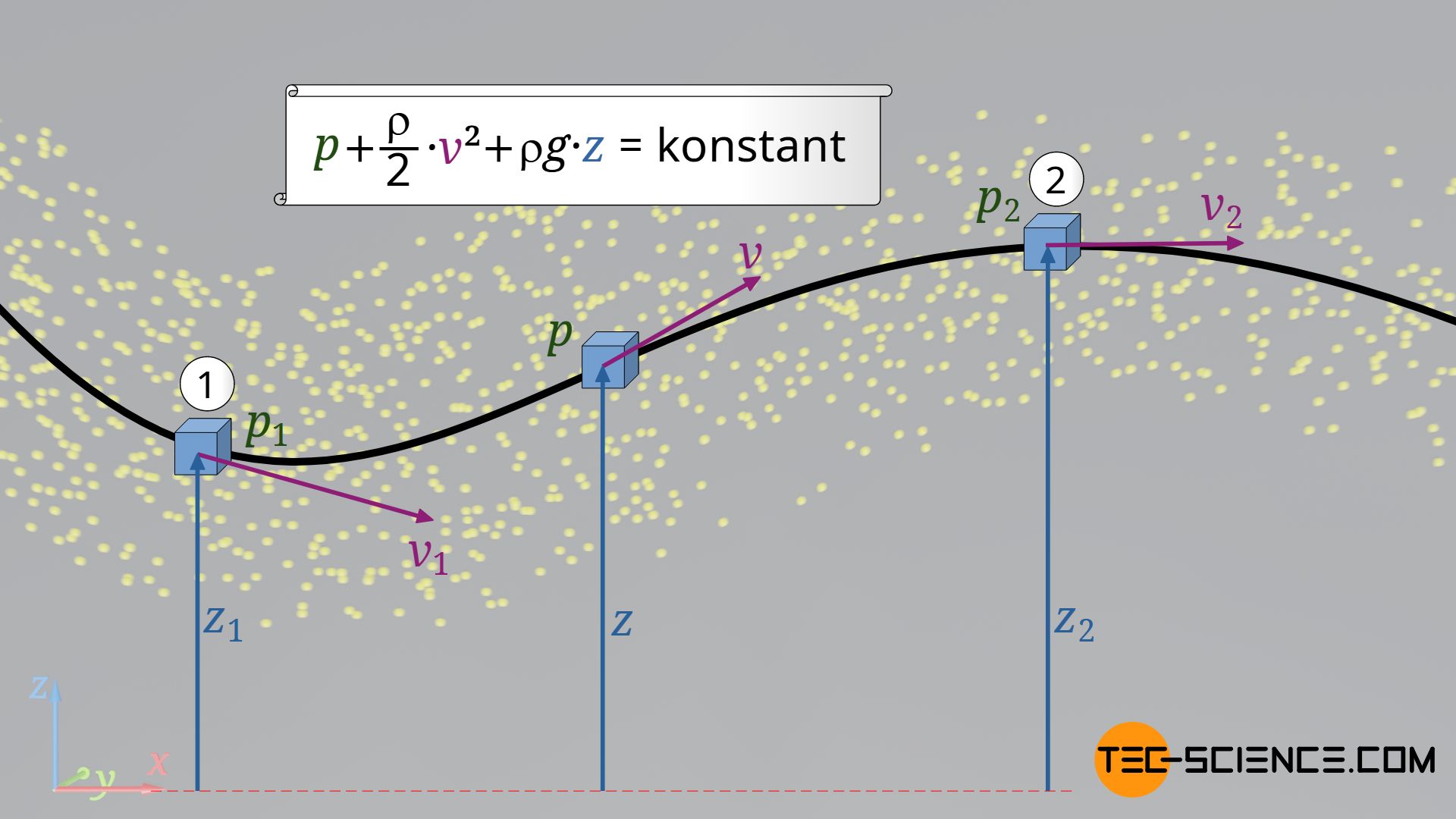
&\boxed{p + \frac{\rho}{2} v^2 + \rho g ~z = \text{konstant}}~~~\text{Bernoulli-Gleichung}\\[5px]
\end{align}

Wir erhalten schließlich die Bernoulli-Gleichung für inkompressible und reibungsfrei strömende Fluide! Diese Gleichung besagt, dass die Summe aus Druckenergie, kinetischer Energie und Lageenergie entlang der Stromlinie konstant ist (Energieerhaltung). Beachte, dass diese Gleichung nur für reibungsfreie, d.h. insbesondere für nicht-viskose Fluide gilt. Zwei Punkte auf einer Stromlinie sind in diesem reibungsfreien Fall somit wie folgt miteinander verknüpft:

\begin{align}
&\boxed{p_1 + \frac{\rho}{2} v_1^2 + \rho g ~z_1 =p_2 + \frac{\rho}{2} v_2^2 + \rho g ~z_2}\\[5px]
\end{align}

Beispiel und praktische Anwendungen der Bernoulli-Gleichung finden sich auch im Artikel Aufgaben und Lösungen zur Bernoulli-Gleichung.