The ideal gas law describes the relationship between pressure, volume, mass and temperature of ideal gases.
Parameters influencing the gas pressure
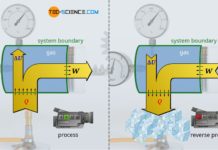
The figure below shows a gas-filled cylinder closed with a piston. If the pressure inside the cylinder is now increased, this becomes noticeable by a force acting on the piston (collisions of gas molecules with the piston surface). To keep the piston in position, a counterforce must be exerted. If, on the other hand, the piston is released, the gas expands and pushes the piston out of the cylinder with a certain force. Due to the high pressure, the gas is therefore able to do work.

Internal combustion engines (generally referred to as heat engines) also work according to the above-mentioned principle. The higher the gas pressure, the greater the work done by the gas. It is therefore of interest that heat engines generate the highest possible pressure. Therefore, the question arises which thermodynamic parameters have any influence on the pressure in a cylinder and which laws are the basis for this. The influencing parameters will be explained in the following. We will consider the gas as an ideal gas.
Experimental setup
The experimental setup shown below is used to investigate the variables influencing the pressure. The setup consists of a glass cylinder and a piston. The cylinder contains air as an approximately ideal gas. The position of the piston can be adjusted by a threaded rod. A valve is attached to the cylinder, through which air can be filled in. The air can also be heated with a Bunsen burner. The pressure in the cylinder can be read on a pressure gauge. How can the pressure in the cylinder be increased?

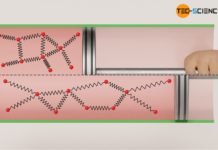
On the one hand, an increase in pressure can be achieved by an increase of the gas mass. This principle is used, for example, when inflating a bicycle tire with an air pump. In doing so, more air molecules are pressed into the tire, which leads to an increase in pressure. The increase in pressure can be explained by the increasing number of collisions taking place per unit time. After all, the gas contains more molecules colliding with an interface, which in this way makes up the pressure.

An increase of the gas mass causes a higher number of collisions of the molecules and thus leads to a higher pressure!
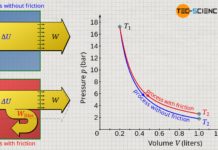
Another possibility to increase the gas pressure in a cylinder is by reducing the gas volume. This is also demonstrated by everyday experience, for example, when the outlet of an air pump is sealed and the piston is pushed at the same time. One will realize that it requires more and more effort to reduce the gas volume more and more. The increased effort is a sign that the gas pressure has increased due to the compression of the gas, which makes it increasingly difficult to compress the gas further.

In the particle model, the increase in pressure when the volume is reduced can be explained by the fact that the gas molecules then take up a smaller volume. The distances that the molecules have to travel in order to collide with the piston surface are shorter and the frequency of collisions therefore increases. This leads to an increased force and thus to an increase in pressure.
A reduction of the gas volume causes an increased collision frequency of the molecules and thus leads to a higher pressure!
Another way to increase the pressure is to increase the gas temperature. Here, too, the increase in pressure is noticeable by an increased force to hold the piston of a cylinder in position. In everyday life, this can be seen, for example, when an air-filled bottle is placed in the sun for some time. The thermal radiation will increase the air temperature in the bottle. If one opens the bottle now, one will hear a hissing sound as a sign of outflowing air. The reason for this is the increased gas pressure inside the bottle, which pushes some air out.

An increase in pressure when gas is heated can be explained by the higher velocity of the gas particles, which is caused by the increased gas temperature (see article Maxwell-Boltzmann distribution). This causes the molecules to collide with other surfaces with more impact, resulting in a greater force and thus increased pressure. This principle of increasing pressure by increasing temperature is used, for example, in combustion engines. A fuel-air mixture is burned in the cylinder and the resulting temperature increase is used to increase pressure. The resulting force causes the crankshaft to rotate.
An increase of the gas temperature causes stronger collisions of the molecules and thus leads to a higher pressure!
Derivation of the ideal gas law
In conclusion, the gas pressure is dependent on …
- gas volume,
- gas mass and
- gas temperature
Since all these quantities describe the state of a gas, they are also called state variables. The mathematical relationship between these variables and the gas pressure (as a further state variable) is clarified in the following.
It can be assumed that a doubling of the gas mass also results in a doubling of the gas pressure, since with twice the number of molecules, twice as many collisions take place within a certain time (also see article Pressure in gases). Thus, the force that these molecules exert on an interface is twice as great and so is the pressure as force per unit area. A tripling of the gas mass should accordingly produce three times the pressure. And indeed, assuming that temperature and volume are kept constant, one can see that the gas pressure p is proportional to the gas mass m:
\begin{align}
\label{m}
&\underline{p \sim m} ~~~~~ T,V=\text{constant} \\[5px]
\end{align}
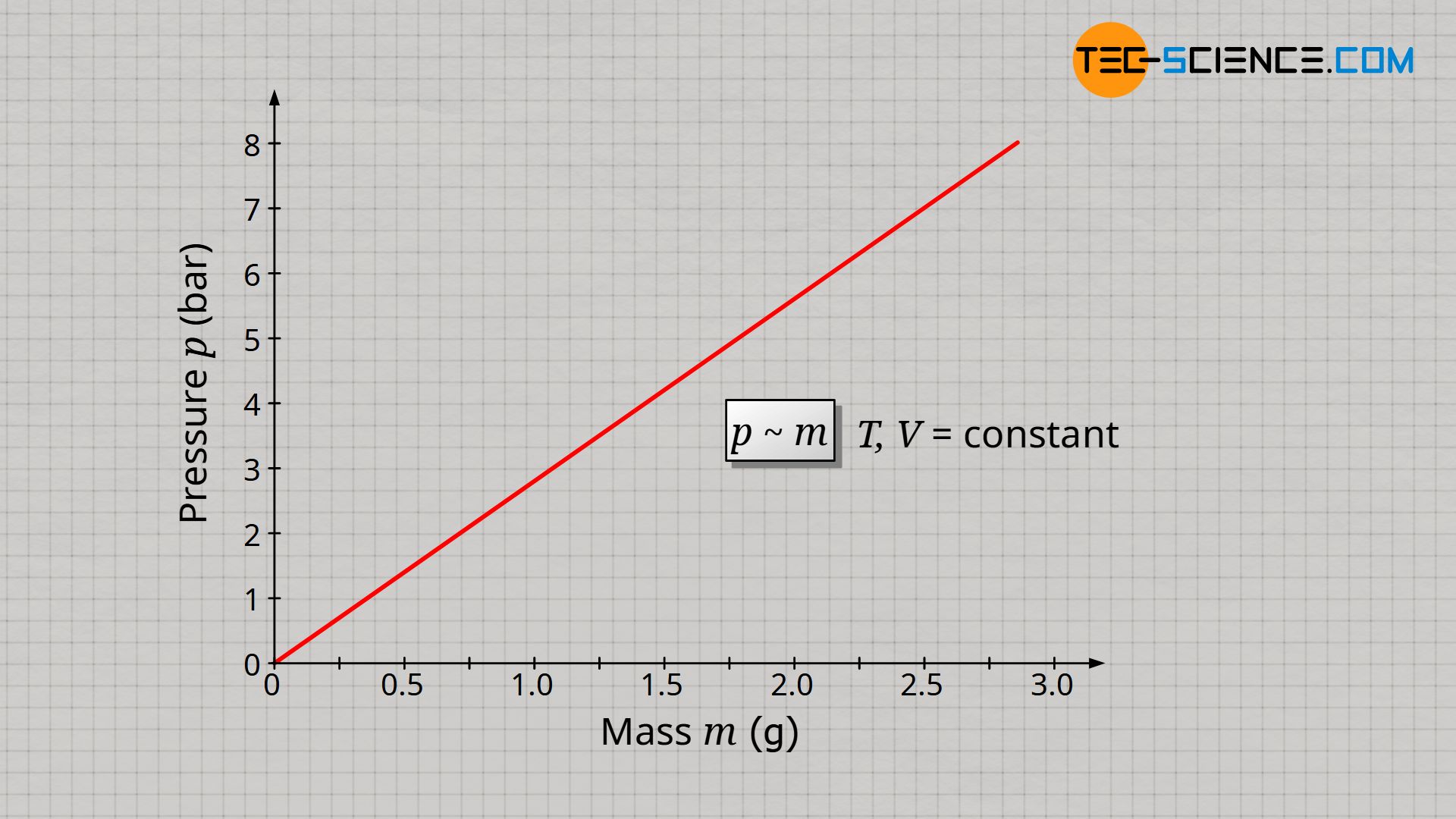
In the same way that an increase in mass influences the gas pressure, a reduction in gas volume should also influence the pressure. Whether the gas mass is doubled at a constant volume or the volume is halved at a constant gas mass has the same effect on the gas molecules: the individual gas particle has, so to speak, only half the space left. Due to the shorter distance to be covered between two collisions, more collisions take place per unit time and the resulting pressure is greater.
The decisive quantity for the gas pressure is therefore the particle density. The particle density is doubled when the gas mass is doubled or also when the volume is halved. And finally, particle density determines how often collisions take place and exert forces on interfaces (more on this later). Assuming that gas mass and gas temperature are kept constant, the gas pressure p is inversely proportional to the gas volume V, since halving the gas volume results in a doubling of the gas pressure:
\begin{align}
\label{v}
&\underline{p \sim \frac{1}{V}} ~~~~~ T,m=\text{constant} ~~~~~\text{(law of Boyle-Mariotte)} \\[5px]
\end{align}
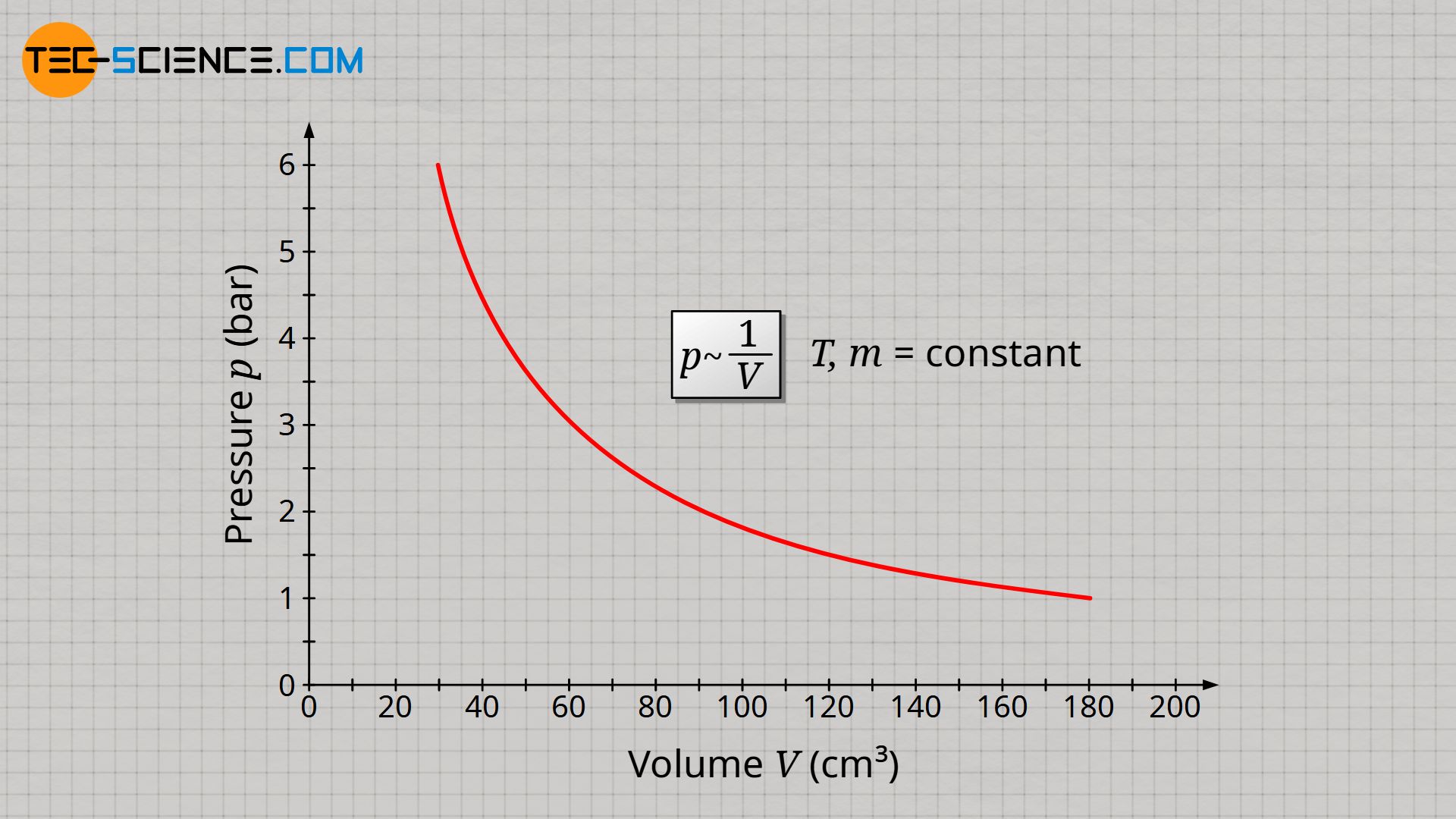
The inversely proportional relationship between pressure and volume at constant temperature and constant mass is also known as Boyle-Mariotte’s law.
The experimental determination of absolute zero in the article Temperature scales had shown that temperature and volume of an ideal gas are proportional to each other if gas mass and gas pressure are kept constant. If now the volume is kept constant, the pressure increases proportionally with the gas temperature. This proportional relationship between pressure p and temperature T is only true if the temperature is given in the unit Kelvin (thermodynamic temperature)!
\begin{align}
\label{t}
&\underline{p \sim T} ~~~~~ V,m=\text{constant} ~~~~~\text{(law of Amontons)} \\[5px]
\end{align}
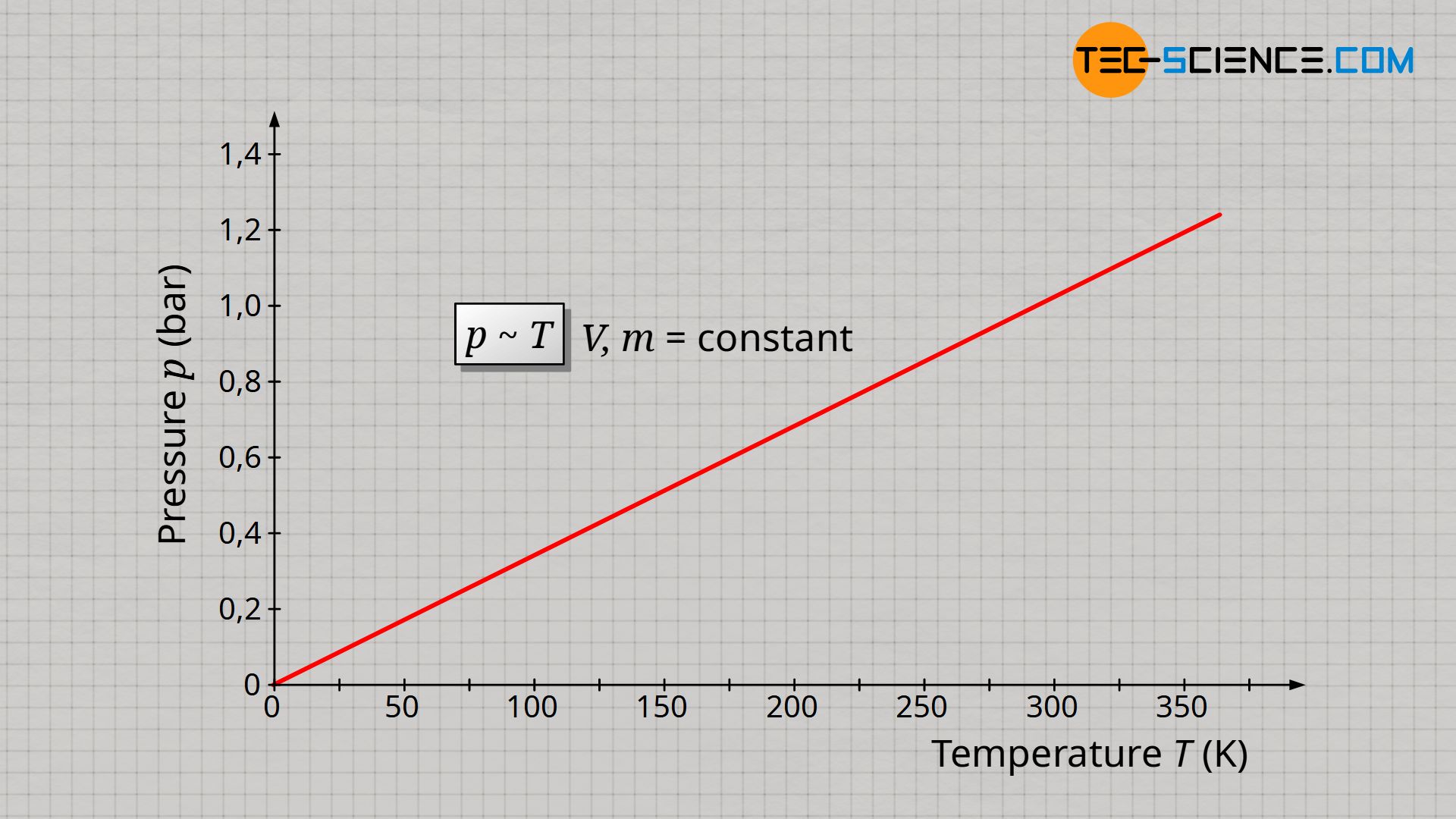
The proportional relationship between pressure and temperature at constant volume and constant mass is also know as Amontons’ law.
The above mentioned laws can finally be transferred into an overall context, so that the gas pressure p is proportional to the gas mass m and the gas temperature T and inversely proportional to the gas volume V:
\begin{align}
&p \sim \frac{m \cdot T }{V} \\[5px]
\end{align}
Thus the quotient of p⋅V and m⋅T is constant and a proportionality constant Rs can be defined:
\begin{align}
\label{p}
&\boxed{\frac{p \cdot V}{m \cdot T} =\text{constant} = R_\text{s}} \\[5px]
&[R_\text{s}] = \frac{{\tfrac{\text{N}}{\text{m²}}} \cdot \text{m³}}{\text{kg K}} = \frac{\text{N} \cdot \text{m}}{\text{kg K}}= \frac{\text{J}}{\text{kg K}} ~~~\text{specific gas constant} \\[5px]
\end{align}
This proportionality constant is called specific gas constant Rs and is only dependent on the type of gas. The specific gas constant describes the relationship between gas mass, gas temperature, gas volume and the resulting gas pressure (absolute pressure!):
\begin{align}
\label{tt}
&\boxed{p = R_\text{s} \cdot \frac{m \cdot T}{V}} \\[5px]
\end{align}
Equation (\ref{tt}) is also called ideal gas law and applies only to ideal gases. In practice, however, many real gases also show a very good agreement with this idealized law. The ideal gas law is very often given in the following form:
\begin{align}
\label{therm}
&\boxed{p \cdot V = R_\text{s} \cdot m \cdot T} ~~~~~\text{(ideal gas law)}\\[5px]
\end{align}
Note that the volume of a gas is a purely geometric quantity and must not be equated with a mass! Due to the incompressibility of water, a water volume of 1 liter can indeed be linked to a mass of 1 kg. However, with compressible fluids such as gases, a direct correlation between volume and mass no longer works. Depending on the pressure, a 1 liter bottle can contain an air mass of 1.2 g (at 1 atm pressure), but also an air mass of 12 g (at an increased pressure of 10 atm).
Specific gas constants of selected gases
The table below shows specific gas constants of selected gases. Note that the specific gas constant depends only on the type of gas and is not influenced by the state of the gas, i.e. it is independent of mass, temperature, volume and pressure!
| gas | specific gas constants Rs J/(kg⋅K) |
|---|---|
| argon Ar | 208 |
| helium He | 2077 |
| nitrogen N2 | 297 |
| oxygen O2 | 260 |
| air | 287 |
| water vapor | 462 |
For each (ideal) gas, the pressure is proportional to the gas mass and the gas temperature and is inversely proportional to the gas volume. However, this generally valid relationship applies to a different extent. This means that, depending on the type of gas (specific gas constant), even with identical gas mass, gas temperature and gas volume, different pressures result. The higher the specific gas constant, the higher the pressure under identical conditions.
For example, air has a specific gas constant of 287 J/(kg·K). This means that air of mass 1 kg, which is contained in a volume of 1 m³ at a temperature of 1000 K (727 °C), causes a pressure of 2.87 bar. If, on the other hand, helium with a specific gas constant of 2077 J/(kg·K) is used instead of air, a pressure of 20.77 atm will result under the same conditions (1 kg gas mass, 1 m³ gas volume and 1000 K gas temperature).
Alternative formulations of the ideal gas law
Dependence on the density
It was explained at the beginning of this article that doubling the gas mass has the same effect on the pressure as halving the gas volume. With the particle model of matter this can be clearly understood: The molecules are closer together and therefore more collisions with interfaces take place per unit time. This leads to an increase in pressure.
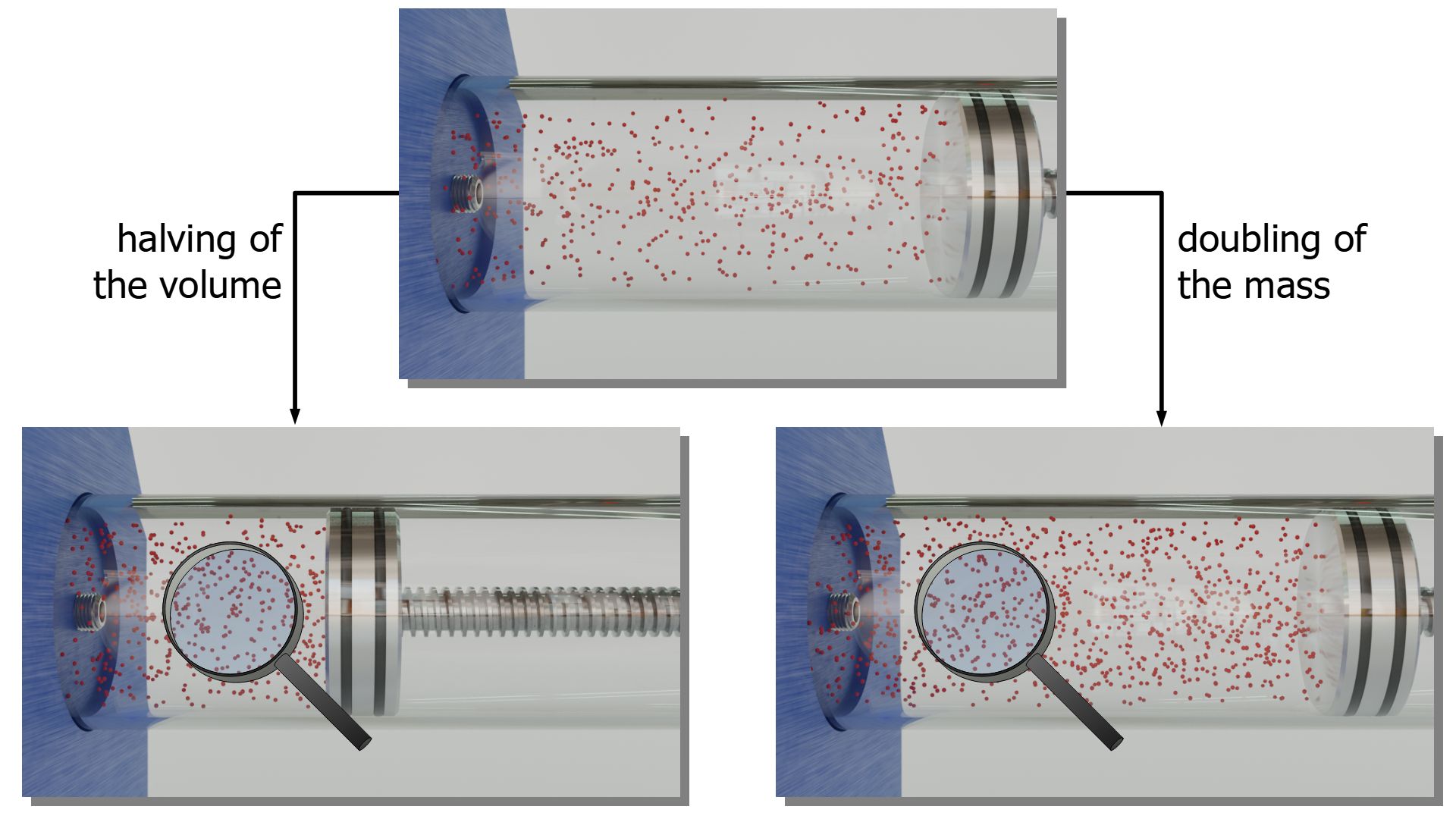
The decisive factor is therefore not the mass or volume per se, but the particle density. The particle density is directly related to the volumetric mass density ϱ, which is the quotient of gas mass m and gas volume V (“mass per unit volume”). That the density is the decisive variable is also directly evident from the ideal gas law (\ref{therm}):
\begin{align}
&p \cdot V = R_\text{s} \cdot m \cdot T \\[5px]
&p = R_S \cdot \frac{m}{V} \cdot T ~~~~~\text{where} ~~~~~ \frac{m}{V}=\rho\\[5px]
&\boxed{p = R_S \cdot \rho \cdot T} \\[5px]
\end{align}
Dependence on the amount of substance
In the ideal gas law (\ref{therm}), the gas mass m can also be expressed by the number of particles n contained in the gas (to be given as amount of substance in the unit mol!) and their molar mass M (unit: kg/mol):
\begin{align}
&p = R_\text{s} \cdot \frac{m}{V} \cdot T ~~~~~\text{where} ~~~~~ m= M \cdot n \\[5px]
&p = R_\text{s} \cdot \frac{n \cdot M}{V} \cdot T \\[5px]
&p = \underbrace{R_\text{s} \cdot M}_{=R_\text{m}} \cdot \frac{n}{V} \cdot T \\[5px]
\end{align}
If the product of specific gas constant Rs and molar mass M for different gases is examined more closely, it turns out that the value of this product is the same for all (ideal) gases:
| gas | specific gas constant Rs [J/(kg⋅K)] | molar mass M [kg/mol] | universal gas constant Rm=Rs⋅M [J/(mol⋅K)] | ||
|---|---|---|---|---|---|
| argon Ar | 208 | x | 0.040 | = | 8.3 |
| helium He | 2077 | x | 0.004 | = | 8.3 |
| nitrogen N2 | 297 | x | 0.028 | = | 8.3 |
| oxygen O2 | 260 | x | 0.032 | = | 8.3 |
| air | 287 | x | 0.029 | = | 8.3 |
| water vapor | 462 | x | 0.018 | = | 8.3 |
Rounded to one decimal place, the value of the product is 8.3 J/(mol⋅K) for all mentioned gases. Minor deviations from this value are due to the fact that the gases listed are not ideal gases but real gases. Helium comes closest to the properties of an ideal gas.
Since the product of specific gas constant Rs and molar mass M is obviously identical for all ideal gases (independent of the actual gas type!), this product is therefore called universal gas constant Rm. More detailed analysis show that the value of the universal gas constant is Rm = 8.3145 J/(mol⋅K).
Finally, the ideal gas law can also be expressed by the amount of substance and the universal gas constant:
\begin{align}
\label{mol}
&\boxed{p = R_\text{m} \cdot \frac{n}{V} \cdot T} \\[5px]
\text{where}~~~ &\boxed{R_\text{m} = 8.3145 \frac{\text{J}}{\text{mol K}}}=R_\text{s} \cdot M \\[5px]
&\text{universal gas constant} \\[5px]
\end{align}
The specific gas constant Rs of a gas can be determined using the molar mass M of the gas and the universal gas constant Rm:
\begin{align}
&\boxed{R_\text{s} = \frac{R_\text{m}}{M}} \\[5px]
\end{align}
Note that there is no gas-specific quantity in equation (\ref{mol})! This equation can be used completely independent of the gas type! Only the amount of substance n must be known. This is also called Avogadro’s law. According to this law, every ideal gas occupies a volume of 22.4 liters per 1 mol of particles under normal conditions (1 atm and 0 °C)!
Under normal conditions, an ideal gas in a volume of 22.4 liters contains 1 mol of particles (Avogadro’s law)!
The question arises why the type of gas is not important for the determination of the pressure according to equation (\ref{mol})? One could think that gases with heavier molecules have a higher kinetic energy and therefore cause a higher pressure when they collide with interfaces compared to lighter molecules. However, the kinetic theory of gases and especially the Maxwell-Boltzmann distribution shows that the mean kinetic energy of a gas molecule Wkin depends only on the temperature T (kB is the Boltzmann constant):
\begin{align}
&\boxed{\overline{W}_\text{kin}=\frac{3}{2}~k_\text{B}~T } \\[5px]
\end{align}
Thus, if the temperatures are identical, the molecules of heavier gases have the same mean kinetic energy as the molecules of lighter gases. Therefore heavier gas molecules have a lower velocity than lighter gas particles. In both cases, however, the mean kinetic energy of a single molecule is identical. For the total pressure, which is ultimately caused by all molecules of a gas, only the particle density n/V is decisive for the pressure besides the temperature.
Dependence on the number of particles
The mole is a count of particles. 1 mol corresponds to a number of particles of 6.022⋅1023. This value is therefore generally used as a conversion factor between the amount of substance n and the number of particles N. This conversion factor is also called Avogadro constant NA. Unlike the particle number N, the Avogadro constant has a unit!
\begin{align}
&\boxed{n=\frac{N}{N_A}} ~~~\text{where } ~~~ \boxed{N_\text{A} = 6.022 \cdot 10^{23} \frac{1}{\text{mol}}} \\[5px]
\end{align}
The ideal gas law can now also be expressed by the number of molecules N instead of the amount of substance n using the Avogadro constant NA:
\begin{align}
&p = R_\text{m} \cdot \frac{n}{V}\cdot T ~~~\text{where} ~~~n=\frac{N}{N_\text{A}} \\[5px]
\label{k}
&p = \underbrace{\frac{R_\text{m}}{N_\text{A}}}_{=k_\text{B}} \cdot \frac{N}{V} \cdot T \\[5px]
\end{align}
The quotient Rm/NA in equation (\ref{k}) consists only of physical constants and is therefore also a constant for all gas types. This term can therefore be defined as a new constant. This constant is called Boltzmann constant kB with a value of 1.381·10-23 J/K.
Finally, the ideal gas law can be expressed by the number of particles N using the Boltzman constant:
\begin{align}
&\boxed{p = k_B \cdot \frac{N}{V} \cdot T} ~~~\text{where} ~~~ \boxed{k_B = 1.381 \cdot 10^{-23} \frac{\text{J}}{\text{K}}} ~\text{Boltzmann constant} \\[5px]
\end{align}
Summary
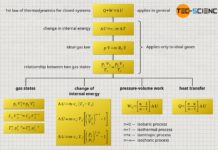
The different forms of the ideal gas law are listed below:
\begin{align}
&\boxed{p \cdot V = R_\text{s} \cdot m \cdot T} \\[5px]
&\boxed{p = R_\text{s} \cdot \rho \cdot T} \\[5px]
&\boxed{p \cdot V = R_\text{m} \cdot n \cdot T}~~~~~R_\text{m} = 8.3145 \tfrac{\text{J}}{\text{mol K}} \\[5px]
&\boxed{p \cdot V = k_\text{B} \cdot N \cdot T}~~~~~k_\text{m} = 1.381 \cdot 10^{-23} \tfrac{\text{J}}{\text{K}} \\[5px]
\end{align}
Linking two states of an ideal gas
With the ideal gas law the specific gas constant of a gas can be determined, if gas pressure, gas volume, gas mass and gas temperature are known:
\begin{align}
\label{0}
&R_\text{s} = \frac{p \cdot V}{m \cdot T} \\[5px]
\end{align}
In most cases, however, one will know the type of gas and therefore its specific gas constant. Therefore one is more interested in one of the state variables. For example, one is interested in the pressure that results from compressing a gas in a piston, heating it and simultaneously increasing the gas mass. Or one could be interested in the temperature that results when a gas is compressed to a certain volume and pressure.
Therefore, the question arises how two states of a gas are generally related to each other. In the following we will therefore consider an ideal gas. Starting from an initial state 1 this gas is brought to a final state 2. This is done by changing the volume, temperature and mass of the gas. As a consequence, the pressure also changes, of course.
In initial state the gas has the pressure p1, the volume V1, the temperature T1 and the mass m1. In the final state the pressure is p2, the volume is V2, the temperature is T2 and the mass is m2. All these state variables will change during the change of state. However, a variable will never change for an ideal gas unless the type of gas suddenly changes due to chemical reactions caused by a change in temperature or pressure: namely the specific gas constant Rs!
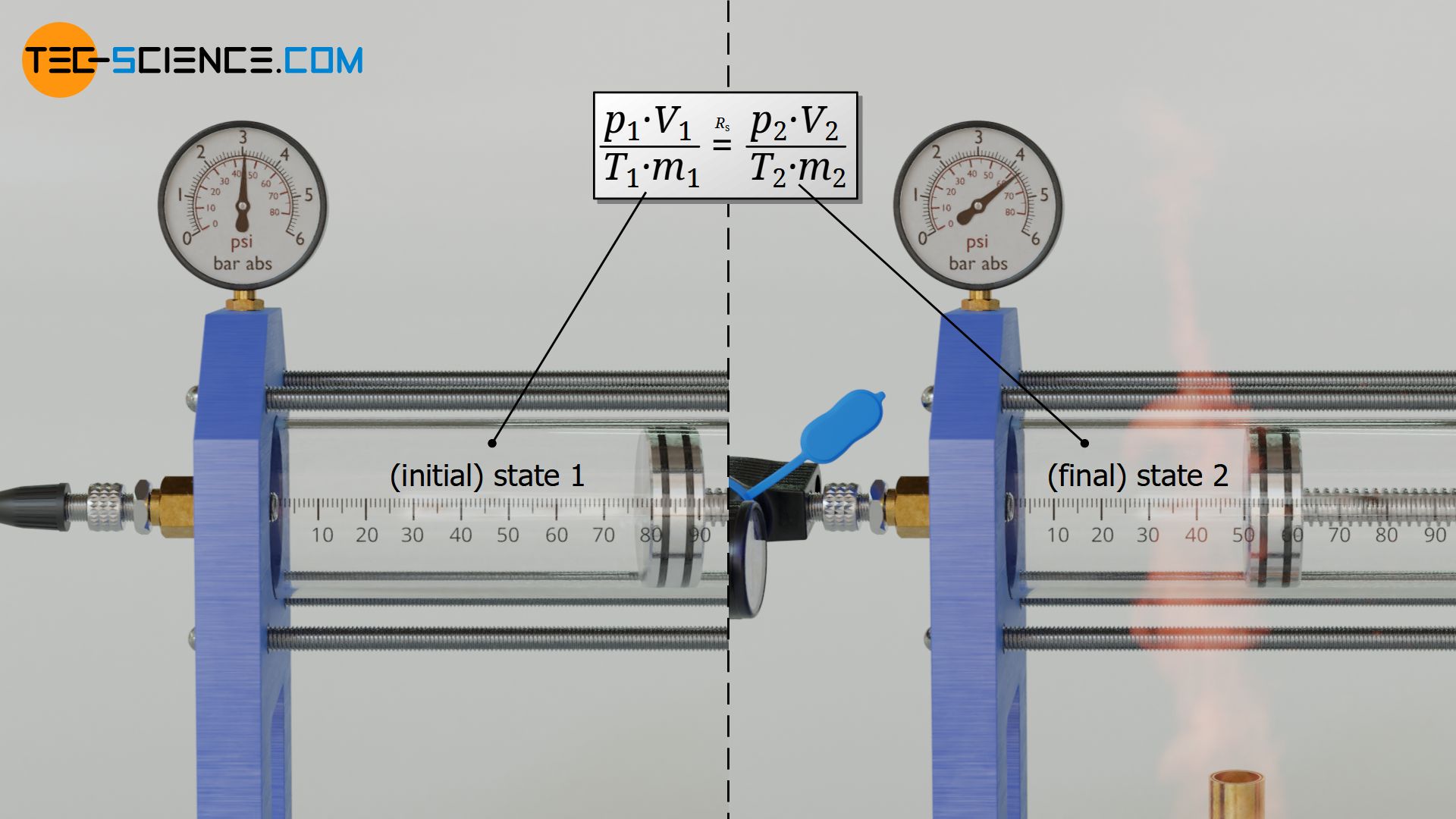
Two states of an ideal gas are therefore linked to each other by the specific gas constant Rs, because this is a material quantity and thus independent of the state of the gas. For both states the same gas constant applies, which is the quotient of the products p⋅V and m⋅T according to equation (\ref{0}). Two gas states are thus generally linked by the following equation:
\begin{align}
&\frac{p_1 \cdot V_1}{m_1 \cdot T_1} = R_S = \frac{p_2 \cdot V_2}{m_2 \cdot T_2} \\[5px]
\label{1a}
&\boxed{\frac{p_1 \cdot V_1}{m_1 \cdot T_1} = \frac{p_2 \cdot V_2}{m_2 \cdot T_2}} ~~~\text{generally applies to ideal gases} \\[5px]
\end{align}
The benefit of equation (\ref{1a}) compared to the ideal gas law (\ref{0}) is, that different gas states can be linked together independent of the gas type, because there is no gas-specific quantity this equation, but only state variables. The exact type of gas is therefore irrelevant for the use of this equation, as long as it is an ideal gas.
Special case for closed systems
Many thermodynamic processes take place in so-called closed systems. This means that the mass of the gas does not change during the change of state. This is the case, for example, during the compression of air in an engine cylinder. Thus, the masses m1 and m2 can be equated in equation (\ref{1a}). The masses cancel each other out. Thus for closed systems, two states are linked only by the gas pressure p, the gas volume V and the gas temperature T:
\begin{align}
\label{b}
&\boxed{\frac{p_1 \cdot V_1}{ T_1} = \frac{p_2 \cdot V_2}{T_2}} ~~~\text{applies to ideal gases in closed systems} \\[5px]
\end{align}
The special cases resulting from equation (\ref{b}) for a change of state
- at constant pressure (law of Gay-Lussac),
- at konstant volume (law of Amontons) and
- at konstant temperature (law of Boyle-Mariotte)
are explained in more detail in the linked articles.