In thermodynamics, reversible processes are processes which are reversible from an energetic point of view!
Introduction
The free adiabatic expansion of an ideal gas in a vacuum showed that this thermodynamic process cannot be described by the isentropic equations, although these equations were derived for an adiabatic system. The adiabatic expansion against a vacuum is an isothermal process in which the temperature remains constant. Therefore, the question arises under which condition a thermodynamic process in an adiabatic system can actually be described with the isentropic equations.
Reversibility of thermodynamic processes
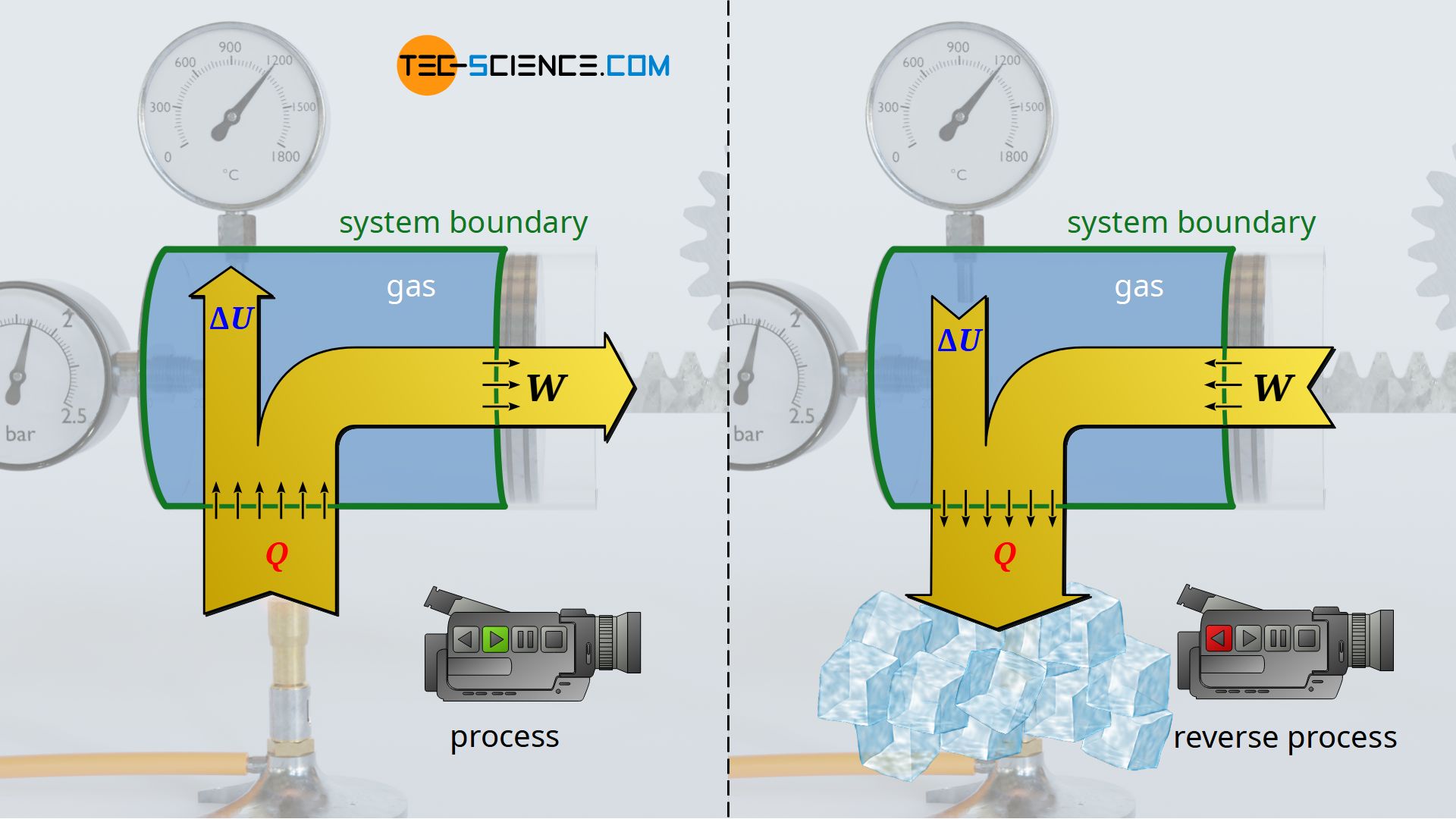
For this purpose, we will take a closer look at different thermodynamic processes. In doing so, we will see that, from an energetic point of view, all these processes can run in one direction as well as, in principle, in the other direction. For example, in the article Concept of pressure-volume work, we looked at a thermodynamic process in which a gas expands in a cylinder by adding heat and finally lifts a weight via a rack and pinion. From an energetic point of view, this process can be reversed in principle.

To do so, one can imagine the original process as being recorded with a video camera, which is then played backwards. In such a reverse case, the weight lowers by removal of heat (cooling). Here, work is no longer done by the gas on the weight, but conversely work is done on the gas by the weight – the gas is compressed by the weight, so to speak. At the same time, cooling lowers the temperature and with it the internal energy. The energy flows are therefore reversed in such a reversal process, without any contradiction arising from experience.
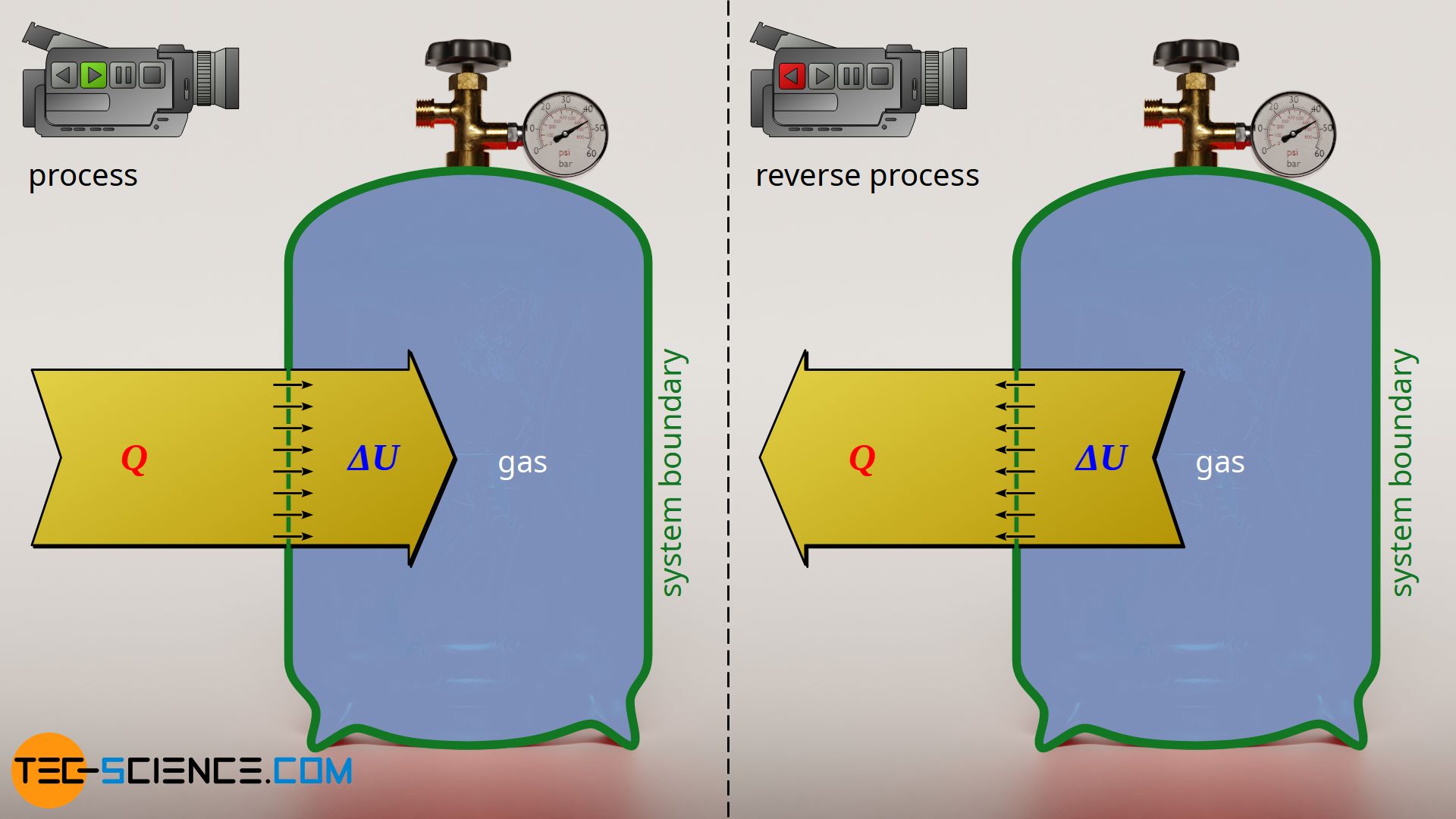
Isochoric process
Such a reversal process can also be found in an isochoric heating of a gas cylinder. The heat supplied causes an increase in internal energy, i.e. the temperature rises. If this process is considered energetically reversed, one would obtain an isochoric cooling. In such a reversal case, the internal energy would decrease due to the dissipated heat and the temperature would decrease.
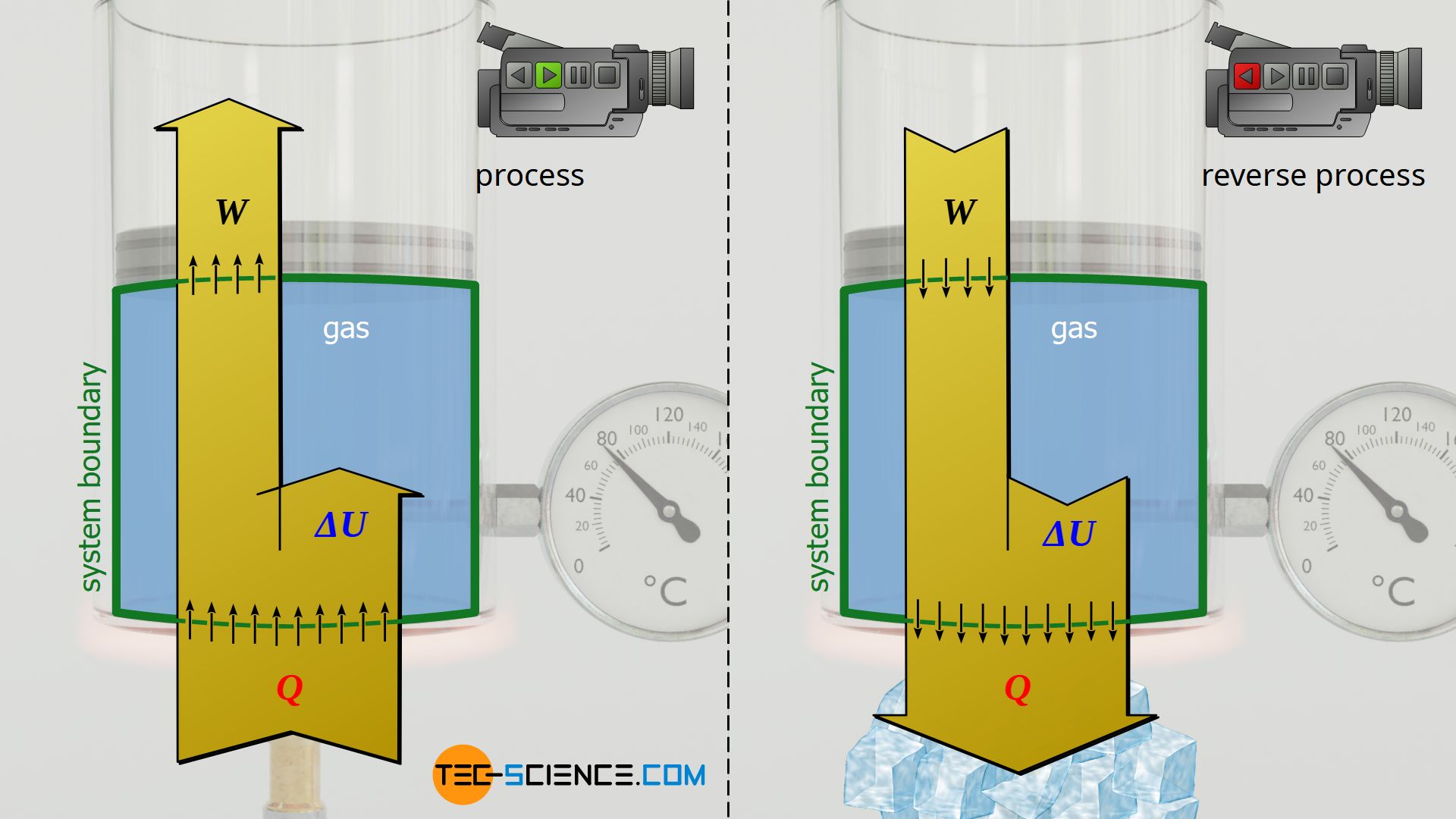
Isobaric process
The process explained in the article on the isobaric process, in which a weight is lifted when heat is supplied, can also be reversed in terms of energy. In the original case, the gas performs work on the weight (lifting) by adding heat, while the internal energy increases and the temperature rises. In the reverse case, an isobaric cooling would be obtained, in which the gas is compressed by the weight (lowering), while at the same time heat is dissipated. The internal energy and thus the temperature are reduced.
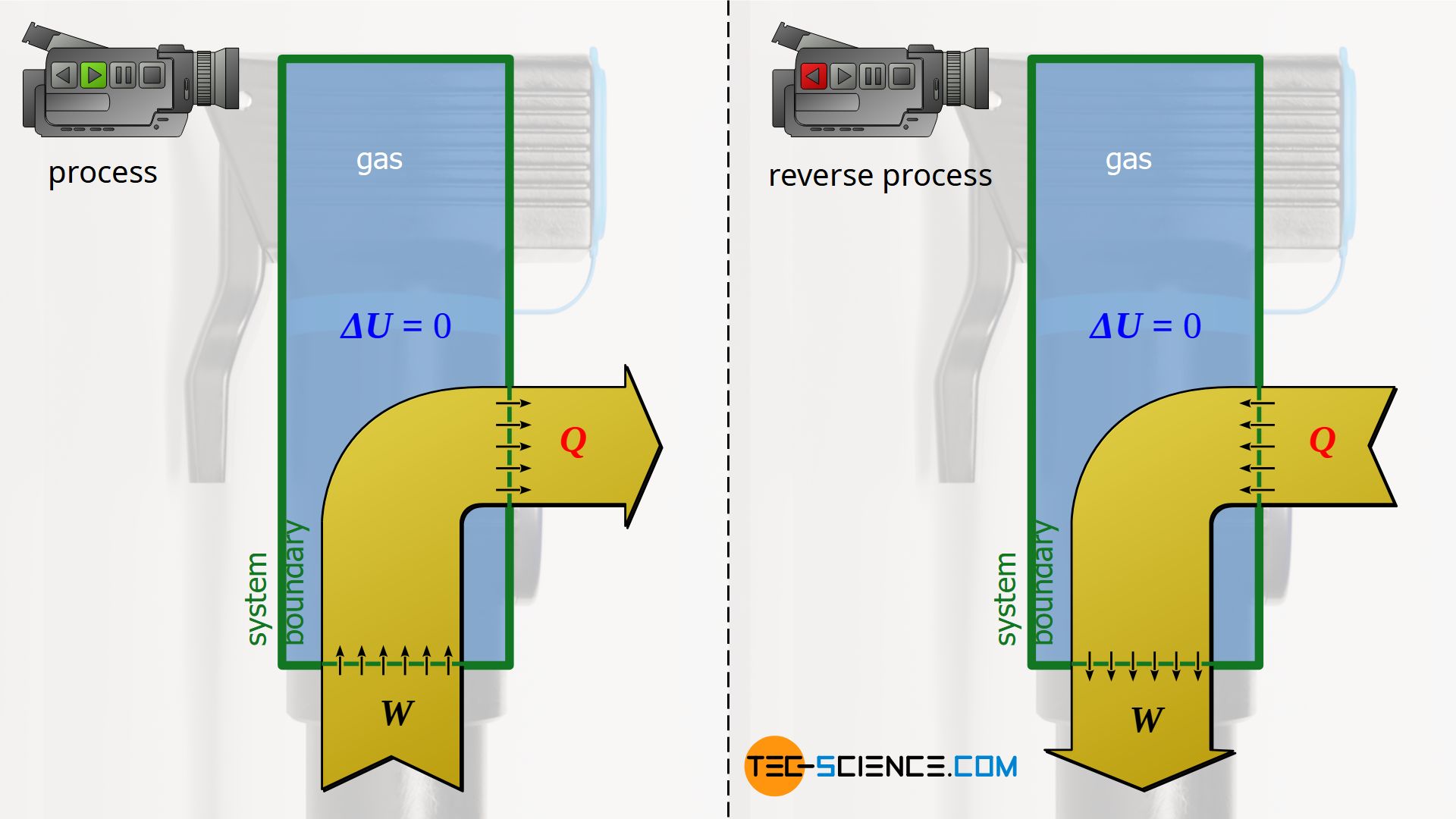
Isothermal process
The compression of air in an air pump explained in the article on the isothermal process also shows such an energetic reversibility. If the gas in an air pump is compressed very slowly with the valve closed, the temperature (nearly) remains constant due to the heat transfer to the surroundings. Conversely, the gas can also expand isothermally from this compressed state. In this case, the expansion must again be very slow so that the surroundings can transfer enough heat to the expanding gas to prevent a drop in temperature.
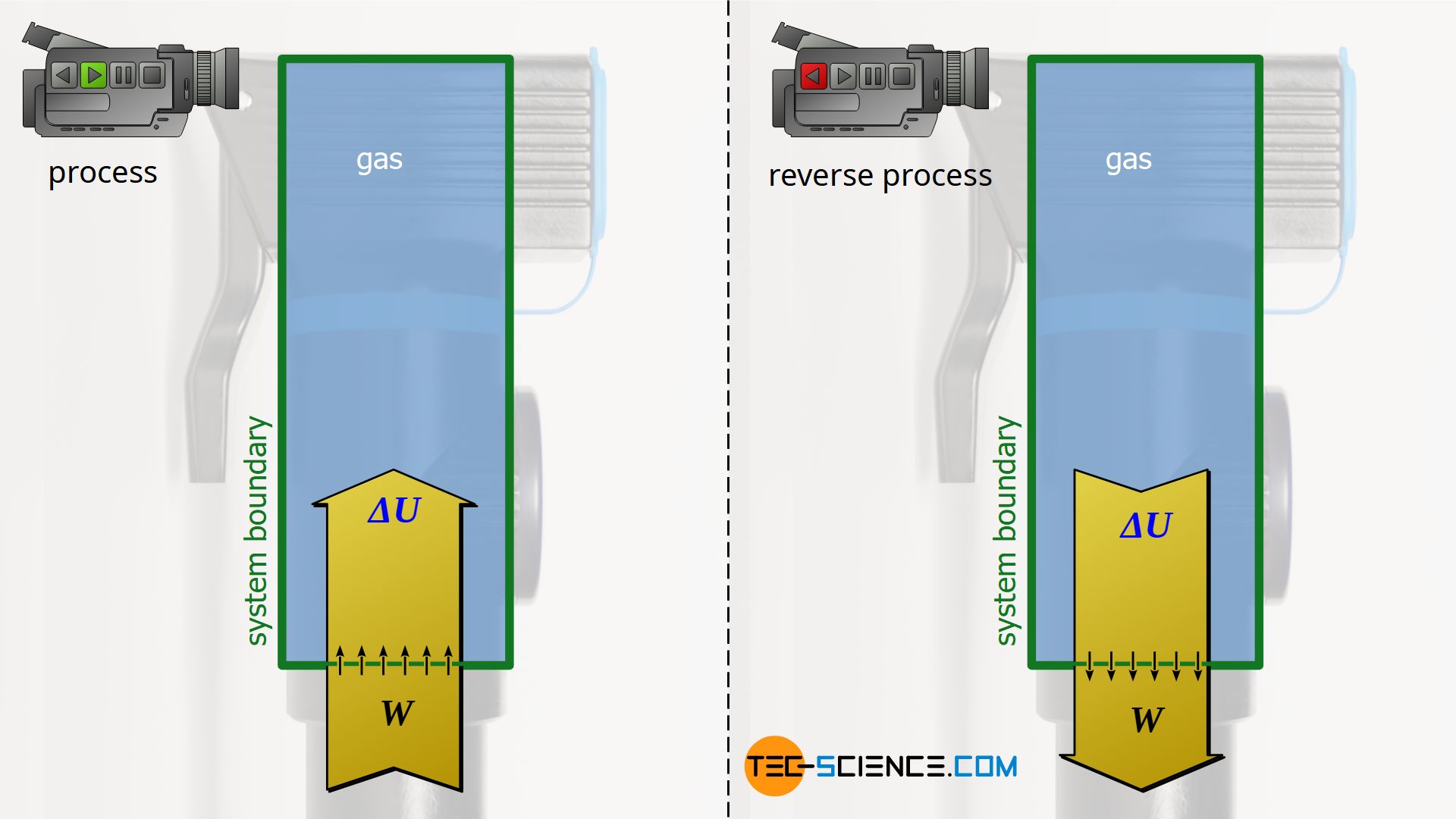
Isentropic process
Also, the rapid compression of air in an air pump presented in the article on the isentropic process can be reversed from an energetic point of view. In the original process, a gas is compressed rapidly (work is done on the gas) so that heat cannot be transferred in such a short time (adiabatic system), which leads to an increase in internal energy and causes the temperature to rise. In the reverse case, the gas expands very rapidly starting from the compressed state. In this isentropic reversal process, work is then done by the gas at the expense of the internal energy and the temperature consequently drops.
Reversibility
The processes considered in the previous sections make it clear that they are all reversible from an energetic point of view. The reversibility of thermodynamic processes presupposes, among other things, that there is no friction or, more generally, no dissipation of energy (e.g. when a piston slides in a cylinder).
In thermodynamics, reversible processes are processes which are reversible from an energetic point of view without violating everyday experience!
Furthermore, the gas states must always be in equilibrium, so that there is no temperature difference within the gas itself. Both the assumption that no energy is dissipated by friction and the assumption of the always existing equilibrium exist, of course, only in the ideal conception. Reversible processes therefore do not exist in reality. However, these ideal conditions have been assumed for all thermodynamic processes considered so far.
Adiabatic expansion against a vacuum as a non-reversible process
As far as reversibility is concerned, however, the situation is different for the free adiabatic expansion of an ideal against a vacuum. This thermodynamic process is not reversible from everyday experience! In adiabatic expansion against a vacuum, the gas expands at constant temperature without transfer of work or heat. For the reverse case, this would have to mean that the gas compresses itself without help.

However, this contradicts all experience, because in order to compress a gas in a cylinder, work must be done on the gas – a gas will not do this by itself. The temperature would then also no longer remain constant, but it would increase due to the work transferred to the gas. Consequently, an adiabatic expansion against a vacuum is a non-reversible process from an energetic point of view. Such non-reversible processes are also called irreversible processes.
Basically all equations presented in the respective articles – in particular those of the isochoric, isobaric, isothermal and isentropic process – are valid only for reversible processes. This now explains why the equations of the isentropic process cannot be applied to the adiabatic expansion against a vacuum: the process is irreversible! The equations of the isentropic process may only be used if it is a reversible process of an adiabatic system. Thus, an isentropic process be defined as follows:
An isentropic process is a reversible thermodynamic process of an adiabatic system!
The reversibility of thermodynamic processes is described by the quantity entropy. For a reversible process of an adiabatic system, the entropy remains constant. Therefore, such a process is called an isentropic process (process at constant entropy).