Derivation of the formulas for work and heat of a polytropic process

In this article you will learn more about the derivation of the formulas for calculating work, heat and change of internal energy for polytropic processes.

Polytropic equations

In the article Polytropic Process in a closed system, the following equations describing polytropic processes were derived and discussed in more detail:

\begin{align}
\label{2716}
\boxed{p \cdot V^n=\text{constant}} &~~\Rightarrow~~ \boxed{p_1 \cdot V_1^n=p_2 \cdot V_2^n} \\[5px]
\label{4375}
\boxed{T \cdot V^{n-1}=\text{constant}} &~~\Rightarrow~~ \boxed{T_1 \cdot V_1^{n-1}=T_2 \cdot V_2^{n-1}} \\[5px]
\label{7991}
\boxed{T^n \cdot p^{1-n}=\text{constant}} &~~\Rightarrow~~ \boxed{T_1^n \cdot p_1^{1-n}=T_2^n \cdot p_2^{1-n}} \\[5px]
\end{align}

The aim of this article is to derive the formulas for calculating work and transferred heat for polytropic thermodynamic processes.

Derivation of the formula for calculating pressure-volume work

The pressure-volume work W_v can generally be calculated by integrating the p(V) function of the polytropic process:

\begin{align}
\label{www}
&\boxed{W_\text{v} = – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V}\\[5px]
\end{align}

Thus, for calculating the work, the function p(V) must be known. If a polytropic process is mathematically described starting from an initial state 1 with pressure p₁ and volume V₁, equation (\ref{2716}) establishes a relationship to any further state 2 with pressure p and volume V. From this, the pressure function p(V) can be determined:

\begin{align}
\label{9891}
&p_1~V_1^n=p~V^n \\[5px]
\label{1227}
&p = \underbrace{p_1~V_1^n}_{=\text{konstant}} \cdot {1 \over V^n} \\[5px]
\label{9377}
&\boxed{p(V)=p_1~V_1^n \cdot {1 \over V^n}} \\[5px]
\end{align}

To calculate the pressure-volume W_v, the pressure function (\ref{9377}) can now be integrated within the limits V₁ to V₂:

\begin{align}
\label{9445}
W_\text{v} &= – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V \\[5px]
&= – \int\limits_{V_1}^{V_2} \underbrace{p_1~V_1^n}_{=\text{constant}} \cdot {1 \over V^n} ~ \text{d}V \\[5px]
&= – p_1~V_1^n~\int\limits_{V_1}^{V_2} {V^{-n}} ~ \text{d}V \\[5px]
&= – p_1~V_1^n~ \left[{1 \over {1-n}}~V^{1-n} \right]_{V_1}^{V_2} \\[5px]
&= – {{p_1~V_1^n} \over {1-n}} ~ \left[V_2^{1-n}-V_1^{1-n} \right] \\[5px]
&= {{p_1~V_1^n} \over {n-1}} ~ \left[V_2^{1-n}-V_1^{1-n} \right] ~~~ \text{factoring out } V_1^{1-n} \text{:} \\[5px]
&= {{p_1~V_1^n~V_1^{1-n}} \over {n-1}} ~ \left[{V_2^{1-n} \over V_1^{1-n}} -1 \right] \\[5px]
\end{align}

\begin{align}
\label{8254}
\boxed{W_\text{V}= {{p_1~V_1} \over {n-1}} ~ \left[\left(V_2 \over V_1 \right)^{1-n} -1 \right]}
\end{align}

The pressure-volume work can be determined relatively easily, especially on the basis of the temperatures. For this purpose, equation (\ref{4375}) is combined with equation (\ref{8254}) and the ideal gas law p⋅V=m⋅R_s⋅T is used:

\begin{align}
W_\text{v} &= {\overbrace{p_1~V_1}^{=m~R_\text{s}~T_1}\over {n-1}} ~ \left[\left(V_2 \over V_1 \right)^{1-n} -1 \right] \text{where: } ~{V_2 \over V_1} = \left(T_1 \over T_2 \right)^{1 \over {n-1}}=\left(T_2 \over T_1 \right)^{1 \over {1-n}}~ \text{ : } \\[5px]
&= {{m~R_\text{s}~T_1} \over {n-1}} ~ \left[{T_2 \over T_1} -1 \right] \\[5px]
\label{m}
&= {{R_\text{s} \over {n-1}}} ~m~ \left(T_2 – T_1 \right) ~~~\text{where } \underline{R_\text{s}=c_\text{p}-c_\text{v}} ~~~\text{:} \\[5px]
&= {{{c_\text{p}-c_\text{v}} \over {n-1}}} ~m~ \left(T_2 – T_1 \right) \\[5px]
&= {{{{c_\text{p}\over c_\text{v}}-1} \over {n-1}}} ~c_\text{v}~m~ \left(T_2 – T_1 \right) ~~~\text{where } \underline{\kappa={c_\text{p} \over c_\text{v}}} ~~~\text{:} \\[5px]
\label{eq:9418}
\end{align}

\begin{align}
\boxed{W_\text{V}=\left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~ \left(T_2 – T_1 \right)}
\label{2604}
\end{align}

Derivation of the formula for calculating transferred heat

According to the first law of thermodynamics, the transferred heat results from the difference between the change in internal energy ΔU and the pressure-volume work W_v:

\begin{align}\
&\boxed{ Q + W_\text{v} = \Delta U} ~~~~\text{first law of thermodynamics}\\[5px]
\label{put}
&Q = \Delta U – W_\text{v}\\[5px]
\end{align}

For ideal gases, the change in internal energy ΔU results – regardless of the thermodynamic process (!) – only on the basis of the temperature change ΔT=T₂-T₁:

\begin{align}\
\label{9719}
&\boxed{ \Delta U = c_\text{v}~m~\left(T_2-T_1 \right)} \\[5px]
\end{align}

If the change in internal energy given by equation (\ref{9719}) and the pressure-volume work according to equation (\ref{m}) are put in equation (\ref{put}), the following formula is obtained for calculating the transferred heat Q of a polytropic process:

\begin{align}
Q &= \Delta U – W_\text{V} \\[5px]
&= c_\text{v}~m~\left(T_2-T_1 \right) – {R_\text{S} \over {n-1}} ~m~ \left(T_2 – T_1 \right) \\[5px]
&= \left[c_\text{v}-{R_\text{S} \over {n-1}}\right]~m~\left(T_2-T_1 \right) ~~~\text{where } \underline{R_\text{S}=c_\text{p}-c_\text{v}} ~~~\text{:} \\[5px]
&= \left[c_\text{v}-{{c_\text{p}-c_\text{v}} \over {n-1}}\right]~m~\left(T_2-T_1 \right) \\[5px]
&= \left[{{c_\text{v}~(n-1)}\over {n-1}}-{{c_\text{p}-c_\text{v}} \over {n-1}}\right]~m~\left(T_2-T_1 \right) \\[5px]
&= \left[{{c_\text{v}~n-c_\text{v}-c_\text{p}+c_\text{v}} \over {n-1}}\right]~m~\left(T_2-T_1 \right) \\[5px]
&= \left[{{c_\text{v}~n-c_\text{p}} \over {n-1}}\right]~m~\left(T_2-T_1 \right) \\[5px]
&= \left[{{n-{c_\text{p} \over c_\text{v}}} \over {n-1}}\right]~c_\text{v}~m~\left(T_2-T_1 \right) ~~~\text{where } \underline{\kappa={c_\text{p} \over c_\text{v}}} ~~~\text{:} \\[5px]
\label{eq:7090}
\end{align}

\begin{align}
\boxed{Q= \left[{{n-\kappa} \over {n-1}}\right]~c_\text{v}~m~\left(T_2-T_1 \right)}
\label{eq:8691}
\end{align}

Summary

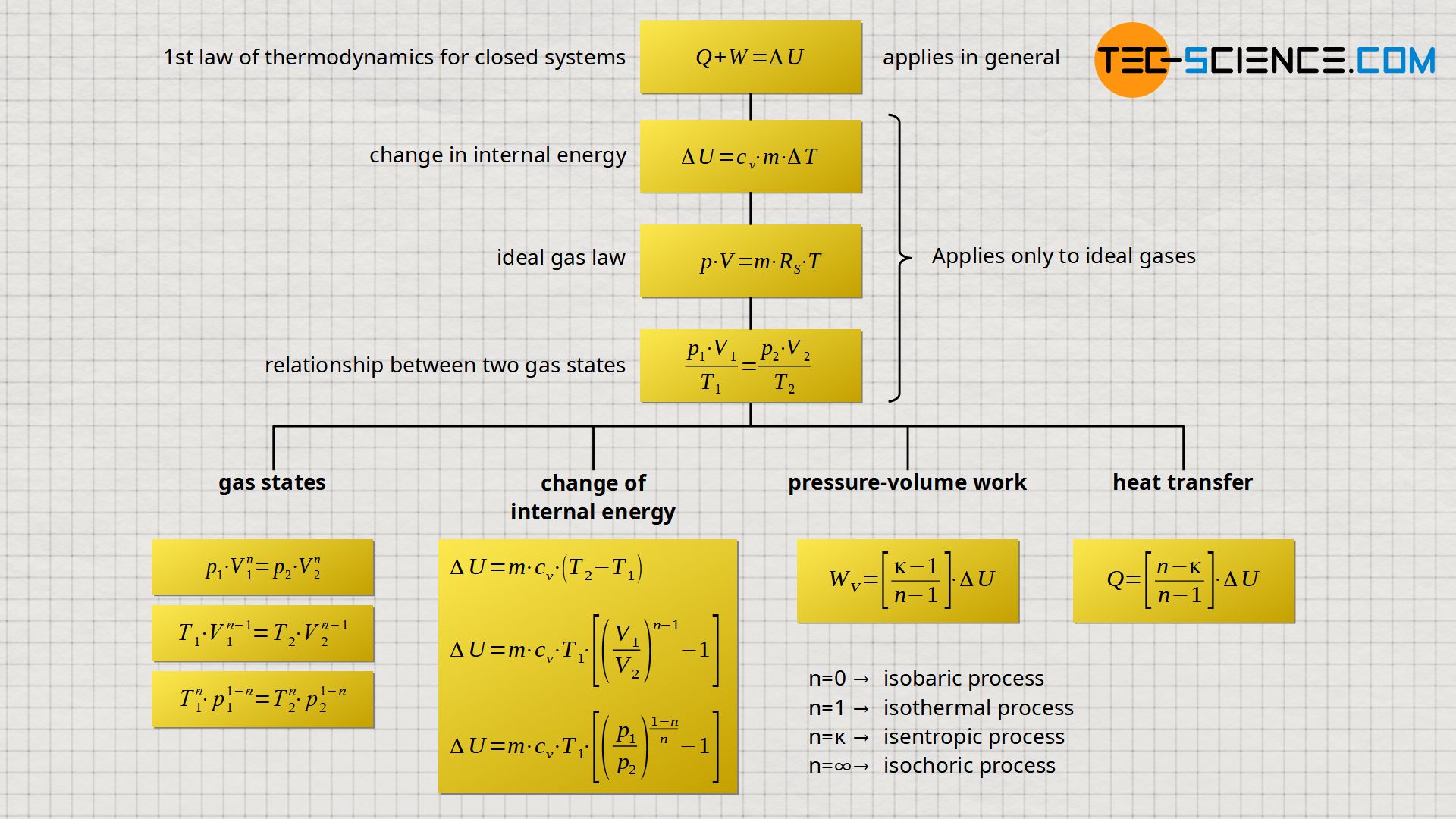
The derived formulas for the calculation of heat, work and change of internal energy, can also be expressed by the volume and pressure ratios using equation (\ref{4375}) and equation (\ref{7991}), respectively:

\begin{alignat}{2}
\label{6005}
&{W_\text{v} = \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~\left(T_2-T_1 \right)}& &= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[\left(T_2\over T_1\right)-1 \right] \\[5px]
&&&= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[20px]
\label{1733}
&{Q = \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~\left(T_2-T_1 \right)}& &= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[\left(T_2\over T_1\right)-1 \right] \\[5px]
&&&= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[20px]
&{\Delta U = c_\text{v}~m~\left(T_2-T_1 \right)}& &= c_\text{v}~m~T_1~\left[{T_2 \over T_1}-1 \right] \\[5px]
&&&= c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&=c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[5px]
\end{alignat}

If we look more closely at equations (\ref{6005}) and (\ref{1733}), we notice that the term c_v⋅m⋅(T₂-T₁) just corresponds to the change in internal energy ΔU. Thus, the pressure-volume work W_v and the transferred heat Q can also be given as a function of the change in internal energy ΔU:

\begin{align}
\label{6763}
&\boxed{W_\text{v}= \left[{{\kappa-1} \over {n-1}}\right] ~\Delta U} \\[5px]
&\boxed{Q= \left[{{n-\kappa} \over {n-1}}\right] ~\Delta U} \\[5px]
\end{align}