Pressure

The pressure describes the force distribution on a surface and is therefore a measure of the magnitude with which a surface is loaded!

Definition

In everyday life one often encounters the concept of pressure. When baking, you press your fingers into the dough to knead it. The feet of a heavy table press into the soft wooden floor and leave pressure marks. A drawing pin is pressed into a wall to hang up a poster.

These examples show that a pressure obviously only arises when at least two objects are involved (finger/dough, table/floor, pin/wall) and exert forces onto each other. The pressure always occurs at the contact surfaces of the two objects.

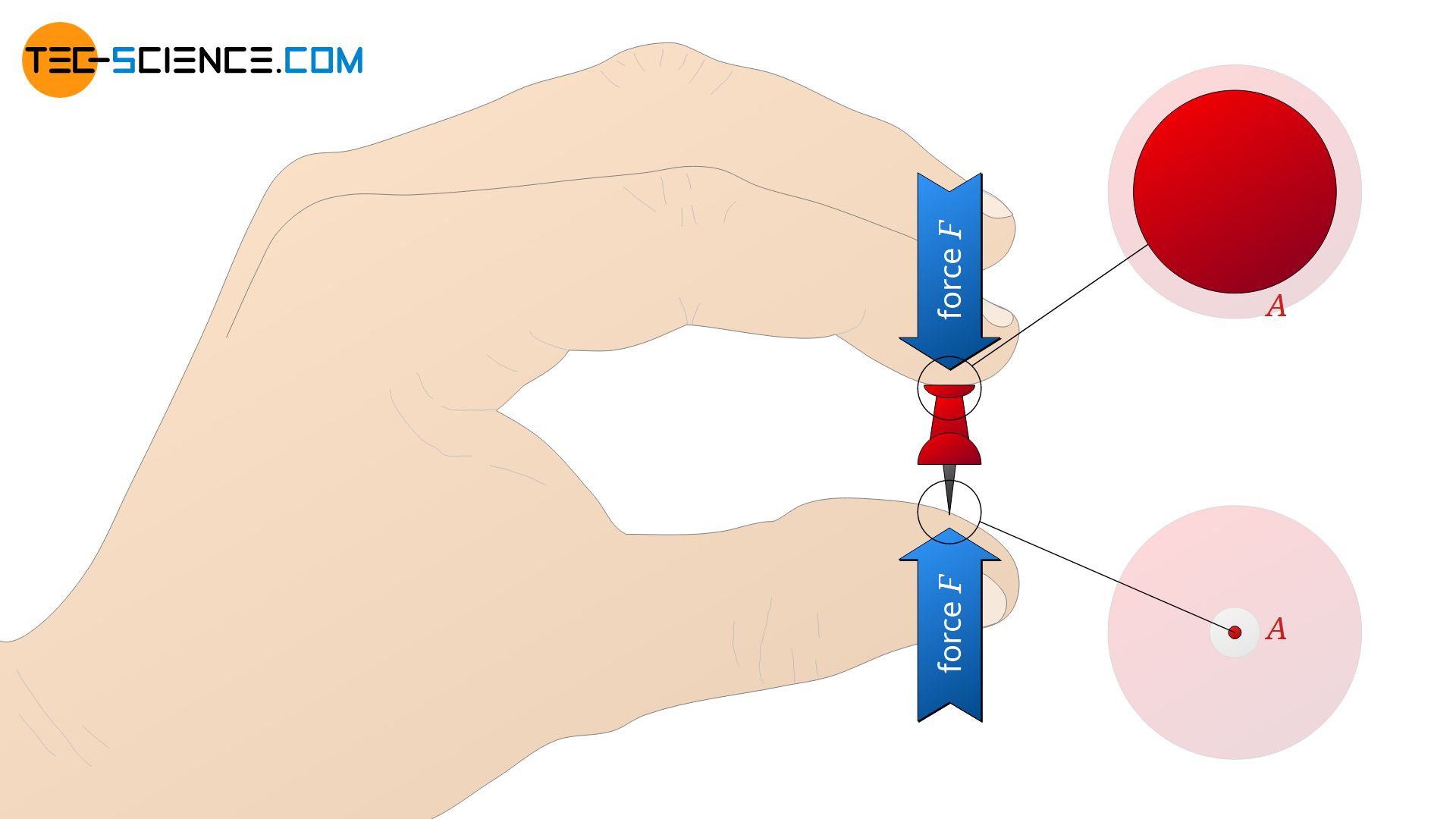
But not only the force is decisive for the magnitude of the pressure. If, for example, one holds a drawing pin between thumb and index finger, one will notice differences when pressing the fingers together, although both sides are subjected to the same force. The tip of the drawing pin presses into the skin much more painfully than the opposite head.

The pressure marks left behind by the feet of the table on a wooden floor will also be deeper, the smaller the contact surface is. In addition to the force, the surface area is also decisive for the magnitude of the pressure.

Everyday experience shows that the greater the force and the smaller the surface area, the greater the pressure. Therefore, it makes sense to define the magnitude of a pressure p as the quotient of force F and surface area A.

\begin{align}
\label{p}
&\boxed{p =\frac{F}{A}}~~~~~[p]=\frac{\text{N}}{\text{m²}}=\text{Pa}~~~\text{(Pascal)} \\[5px]
\end{align}

The pressure thus describes the force distribution on a surface (force per unit area) and has the unit N/m². This unit is often referred to as Pascal (unit: Pa). For example, a pressure of 300 N/m² means that there is a force of 300 N per square meter of area.

The pressure describes the force distribution on a surface and is therefore a measure of the magnitude with which a surface is loaded!

Pressure in liquids and gases

The above mentioned examples are always solid objects which exerted pressure onto each other. In this context one also speaks of solid pressure. But not only solid objects can exert forces on other solid objects and thus, depending on the contact area, exert pressures. Gases and liquids (both referred to as fluids) can also exert forces and thus pressures on interfaces. In this context one speaks of fluid pressure.

The pressure of a gas can be observed, for example, when a car tire is inflated. The air is obviously able to lift the car a little during inflation. The required force results from the air pressure in the tire. Also liquids are able to exert forces and thus pressures. One thinks for example of the hydraulic oil of a jack, by whose pressure a piston is lifted with large force.

In contrast to the solid pressure which, to put it simply, acts only in a certain direction, the fluid pressure of gases or liquids acts in all directions in the same way. In this way, for example, the gas pressure of a car tyre is able to keep the tyre stable in shape in any direction. Also the pressure in a liquid will have the same effect in all directions.

In contrast to the “solid pressure” of solid objects, the “fluid pressure” in gases or liquids acts equally in all directions!

The following experiment can easily prove that the pressure in liquids and gases acts equally in all directions. For this purpose a rubber cushion is filled with water. Tubes are attached to different points of the cushion. At the other end of the tubes there are pressure gauges. Now one squeezes the cushion at any place. One will notice that not only the pressure rises near the contact point, but all pressure gauges equally. Obviously, the pressure is the same at all points of the liquid. Instead of water, the experiment can also be carried out with gas, e.g. air. The result will be the same.

The fact, that the fluid pressure within liquids and gases acts equally in all directions, is based on the free movement of the particles within. Since the particles do not show preferred directions of motions, they collide with all adjoining surfaces the same way. Thus the forces resulting from these collisions, which make up the pressure, are identical into all directions. This phenomenon is described by the so-called equipartition theorem. More detailed information on pressure in gases can be found in the article Gas pressure.

Pressure of liquids and gases on curved surfaces

The figure below shows a gas (or liquid) in a cylinder, which is closed by a piston. The force exerted by the fluid on the piston can be calculated as the product of pressure p and piston surface area A according to the definition of pressure:

\begin{align}
\label{a}
&F = p \cdot A \\[5px]
\end{align}

Until now, a flat surface was assumed on which the pressure acts and thus exerts forces. But how does the force change if it is no longer a flat but a curved surface? The figure below shows a piston whose surface is no longer flat (the surface on which the pressure is applied is coloured yellow for better visibility).

Due to the curvatures, the piston now has a larger surface area. One could therefore come to the premature conclusion that the enlarged piston surface also increases the force on the piston according to the equation (\ref{a}). In fact, however, the force on the piston will be the same! So the shape of the surface has no influence on the force caused by the pressure.

A simple example from everyday life can be used to demonstrate this phenomenon. To do this, one simply holds the piston in the air without a cylinder. In this case, both sides of the piston are exposed to the same atmospheric pressure. This atmospheric pressure is caused by the surrounding air molecules which collide on both sides of the piston. Obviously, the piston is not pushed in either direction, but remains at rest. Since the piston is in equilibrium, the force exerted by the ambient pressure on the flat surface must be as great as on the curved surface.

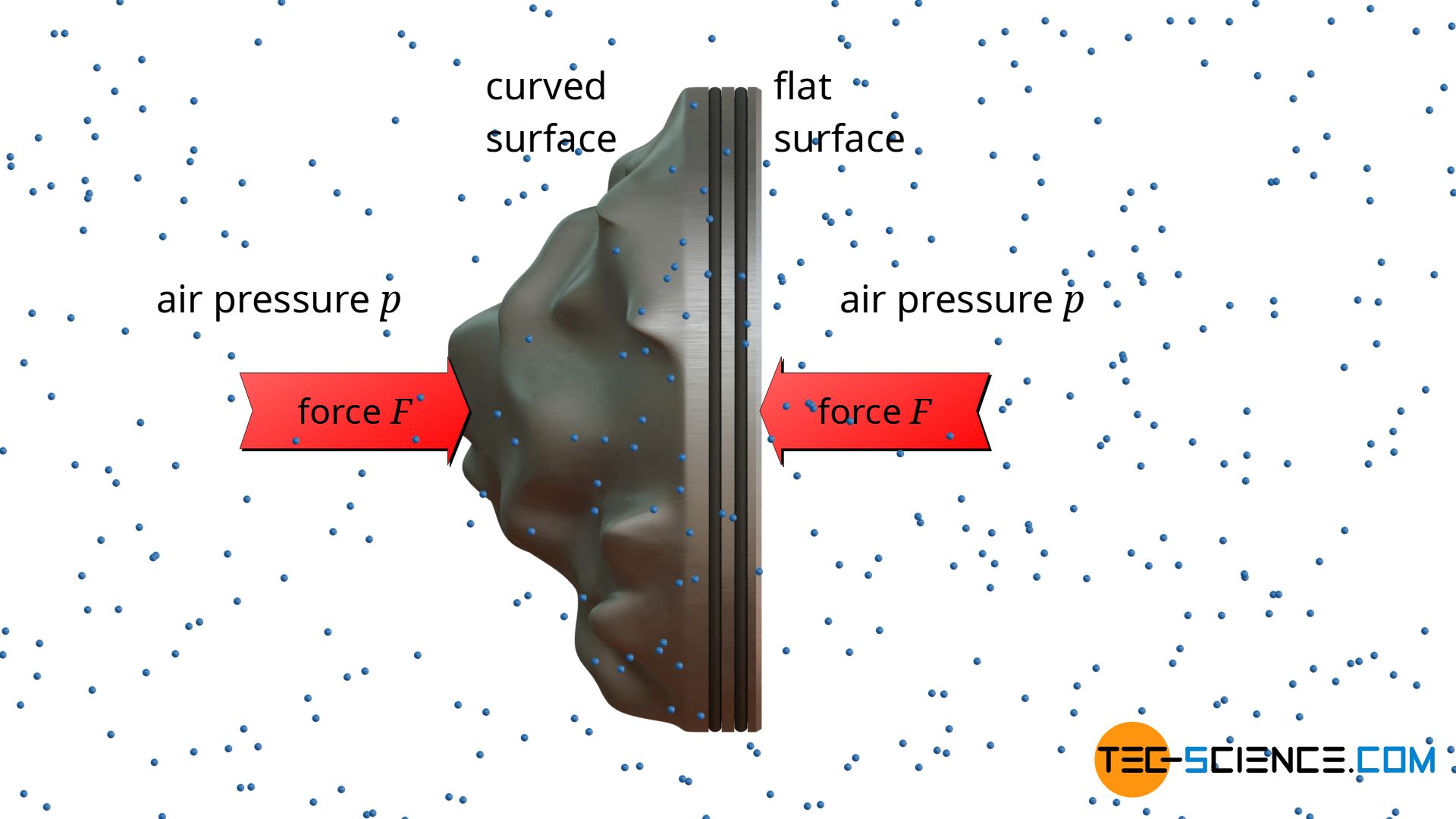
In a nutshell, the calculation of the force on a curved surface is therefore always based on the flat surface; to be more precise: the surface area projected in the direction of the force. One can imagine irradiating the curved surface with a flashlight in the direction of the force. The area of the resulting shadow on a flat wall corresponds to the surface projected in the direction of the force.

To calculate the force exerted by the pressure of a gas or liquid on any curved surface, the area projected in the direction of the force must be taken as a basis!

One can also explain this fact very well. For this one imagines the curved surface as built up by many steps (which is the case on a more atomic level by the atoms). Only surfaces arranged perpendicular to the direction under consideration generate an effective force when the fluid molecules collide with the surface (arrows marked yellow). If particles collide with sideward surfaces, these will also produce force, however not in considered direction but perpendicular to it (white arrows). Thus it becomes clear that only surfaces are relevant which are arranged perpendicular to the considered force. This corresponds to the projected area!

Compressibility & Incompressibility

Even though gases and liquids are very similar in terms of their spatial pressure effect, there is one decisive difference. This is evident when one tries to compress a gas and a liquid, i.e. to reduce the volume. If one confines the air to a cylinder and compresses it with a piston, then the gas pressure rises strongly with volume reduction. If, however, a liquid is used instead of the gas, then the liquid pressure also rises strongly, but (almost) without a reduction in volume.

In contrast to gases, liquids cannot be compressed. This also applies to many solids, such as metals. Such materials, which do not change their volume under pressure, are also called incompressible. Substances such as gases, which change their volume very strongly under pressure, are called compressible.

Incompressible substances are substances which do not change their volume under pressure!

Note that the term incompressibility refers only to the volume of the material and not to the shape. A steel cube will change its shape under the high pressure of a press, but not its volume. The volume is determined solely by density and mass. Since the density ϱ is a material constant and the mass m does not change during deformation, the volume V remains constant (V=m/ϱ). Steel is therefore incompressible despite its changeable shape! This also applies to liquids, which can change their shape but not their volume.