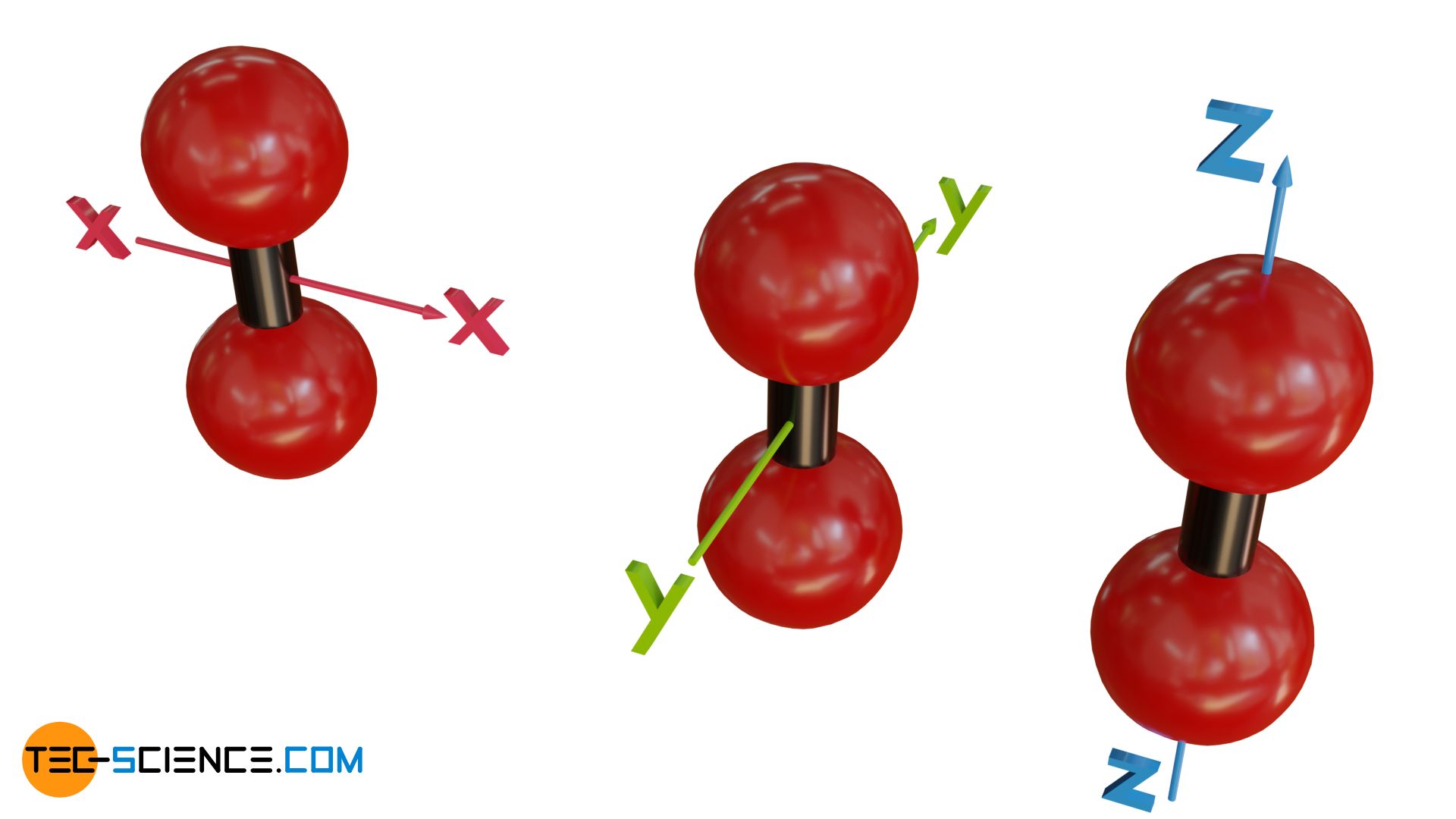
The equipartition theorem states that the kinetic energy of the gas molecules is equally divided along all three spatial directions!
Equipartition theorem
In the article Pressure and temperature the following equation was derived to calculate the pressure p exerted by an ideal gas:
\begin{align}
\label{druck}
& \boxed{p = 2 \cdot \frac{N}{V} \cdot \overline{W_{kin,x}}} \\[5px]
\end{align}
In this equation, N denotes the number of particles in a gas volume V (e.g. in a cylinder). Wkin,x refers to the mean kinetic energy with which the molecules collide with a boundary surface and thereby exert the pressure p (e.g. on a piston). The kinetic energy refers only to those velocity components with which the particles actually hit the boundary surface (here: the velocity components along the x-direction). Speed components directed perpendicular to the surface (in y- and z-direction) do not lead to an impulse on the piston and are therefore not relevant for the pressure on the piston.

At first glance, the pressure given by the equation (\ref{druck}) refers only to the pressure exerted by the gas in the x-direction. For the other spatial directions a pressure can be defined analogously, which is connected with the kinetic energies in the corresponding directions:
\begin{align}
\label{pi}
& p_i = 2 \cdot \frac{N}{V} \cdot \overline{W_{kin,i}} ~~~~~i=x,y,z \\[5px]
\end{align}
However, practice shows that the pressure in gases is equally present in all spatial directions. To verify this, the cylinder sealed with a piston can be equipped with three pressure gauges. These are mounted at right angles to each other on the cylinder, so that the pressure exerted by the gas in the various spatial directions can be measured separately. In fact, you will find that the pressure in all three directions is identical.

Now the gas in the cylinder is compressed by suddenly pushing the piston into the cylinder. The moving piston then hits the oncoming molecules in the gas with great force. On a microscopic level, this process is similar to hitting an oncoming ball with a racket. The moving piston thus increases the speed of the molecules in the (negative) x-direction. This also increases the mean kinetic energy that is related to the x-direction (which also explains the increase in temperature during compression).
Consequently, the compression should only increase the pressure in the x-direction and the pressures in the y- and z-direction should remain unaffected. However, this will not be found in practice! Experience shows that even with such a compression the pressure will increase equally in all spatial directions. According to the equation (\ref{pi}), the kinetic energy must have increased equally along the three spatial directions. Obviously the supplied energy during compression must have been divided equally among all three spatial directions. This phenomenon is also called equipartition theorem.
The equipartition theorem in connection with ideal gases states that the kinetic energy of the particles (or the gas) is equally divided along all three spatial directions and thus the pressure in all spatial directions is identical!
The equipartition theorem is a direct consequence of the random, statistical motion of the particles. These “chaotic” movements of the particles leads to continuous collisions in which the particles subsequently move in different directions. In this way, the originally ordered motions quickly become disordered motions in which no direction is preferred and thus an equal distribution of speed and energy takes place.
The equipartition theorem is not limited to translational motion but applies to all forms of energy at the atomic level. The next section deals with this in more detail.
Distribution of energy among degrees of freedom
In the article “Pressure and temperature” it was shown that the mean kinetic energy of a particle Wkin (now no longer limited to one direction but to be understood as “total” kinetic energy of a molecule!) is related to the thermodynamic temperature T as follows:
\begin{align}
\label{kin}
& \boxed{\overline{W_{kin}} = \frac{3}{2} k_B \cdot T} \\[5px]
\end{align}
For the overall energy of the ideal gas with a total of N particles, the following internal energy applies:
\begin{align}
\label{u}
& \boxed{U = \frac{3}{2} N k_B T} \\[5px]
\end{align}
Translation
The three dimensions in which the molecules of an ideal gas can move ultimately stand for the possibilities the gas has to store energy. A particle can put its energy into the motion along the x-direction as well as into the motion in y- or z-direction. These possibilities to store energy are also called degrees of freedom.
In thermodynamics, degrees of freedom are the number of possibilities to store energy at the atomic level!
A molecule of an ideal gas thus has a total of three degrees of freedom – for each spatial direction a possibility to store energy in the form of a translational motion. For each degree of freedom f (i.e. for each spatial direction) an energy of ½⋅kB⋅T is assigned for a particle or for the entire gas an (internal) energy of ½⋅N⋅kB⋅T per degree of freedom.
\begin{align}
\label{frei}
&\boxed{W = \frac{f}{2} k_BT} ~~\text{energy of a particle}\\[5px]
\label{inn}
&\boxed{U = \frac{f}{2}Nk_BT} ~~\text{internal energy of the gas}\\[5px]
\end{align}
Rotation
Whereas only three degrees of freedom in terms of the three spatial dimensions are possible for translational motion in monatomic gases, rotational motion can also occur in molecules with two atoms (or more generally: linear molecules). This theoretically results in three further possibilities to store energy: in the form of rotation around the x-axis, the y-axis and the z-axis. Theoretically in this case you get a total of f = 6 degrees of freedom.
One will also notice an equal distribution among these individual possibilities to store energy, regardless of whether it is a translational or rotational motion! Imagine that the linear molecules in a gas are initially only given a translational motion in one direction, but then sooner or later the molecules will begin to rotate due to the collisions between the molecules. Due to the random motion, the originally purely translational kinetic energy will gradually be converted into rotational energy and divided equally among all degrees of freedom. For example, the translational kinetic energy in the x-direction will then be the same as the angular kinetic energy around the y-axis.
The equipartition theorem states that the total energy is divided equally among each degree of freedom!
Note that the temperature is determined exclusively by the translational kinetic energy of the particles, regardless of whether the molecules rotate or not! Thus, at a given temperature, the same amount of energy will always be attributed to the translational motion, which is determined by equation (\ref{kin}). According to the equipartition theorem, the same amount of energy must then be in the rotational motion, as long as the molecules can rotate! Therefore, equation (\ref{frei}) also applies to each degree of freedom of a rotational motion. Analogously this applies to equation (\ref{inn}). A gas with linear molecules with a total of 6 degrees of freedom at the same temperature thus contains twice the (internal) energy compared to a monatomic gas with only three degrees of freedom (assuming the same number of particles).
Note that, for quantum mechanical reasons, not all theoretically possible degrees of freedom can actually be used. For example, with molecular hydrogen (dihydrogen), a very high energy is required for the hydrogen molecule to rotate around the molecular axis (rotation around the z-axis in the figure above). At “normal” temperatures, the energy stored in the gas is usually not sufficient to cause the molecule to rotate around this axis. The use of this rotational energy is therefore only theoretical for the time being. One also speaks of a so-called “frozen” degree of freedom, since this is only actually present at high thermal energies or temperatures. The hydrogen molecule, like many other diatomic molecules, therefore only effectively has five degrees of freedom.
Note: In many cases, the atoms are assumed to be mass points, including the individual atoms of linear molecules. In this case, no energy can be stored around the molecular axis anyway, since effectively no mass is in rotation (no moment of inertia)! In this model, such a two-atom molecule then has only two degrees of freedom for rotation anyway! Therefore in most cases we speak of two degrees of freedom for rotation and not of three. The consideration as mass points also makes sense insofar as one would otherwise have had to take rotational energies into account even for monatomic gases (after all, spherical atoms can also rotate and thus store energy). In addition, practice shows that in most cases only two degrees of freedom are effectively available anyway for the rotational movement of diatomic molecules.
Vibration
Diatomic molecules (dumbbell molecules)
In the case of diatomic molecules, it must be noted that there are generally also binding energies between the particles, which act similarly to an elastic spring. Due to these elastic bonding forces, the molecule can also oscillate (vibrate) along the molecular axis. One might think that this is only one degree of freedom. In reality, however, vibrations contain both potential energies and kinetic energies. For this reason, two degrees of freedom always apply to possible directions of oscillation.

Triatomic linear molecules
Triatomic linear molecules, for example, can vibrate in four different ways, so that eight degrees of freedom effectively result. Such vibrational degrees of freedom are also referred to as normal modes of vibration.
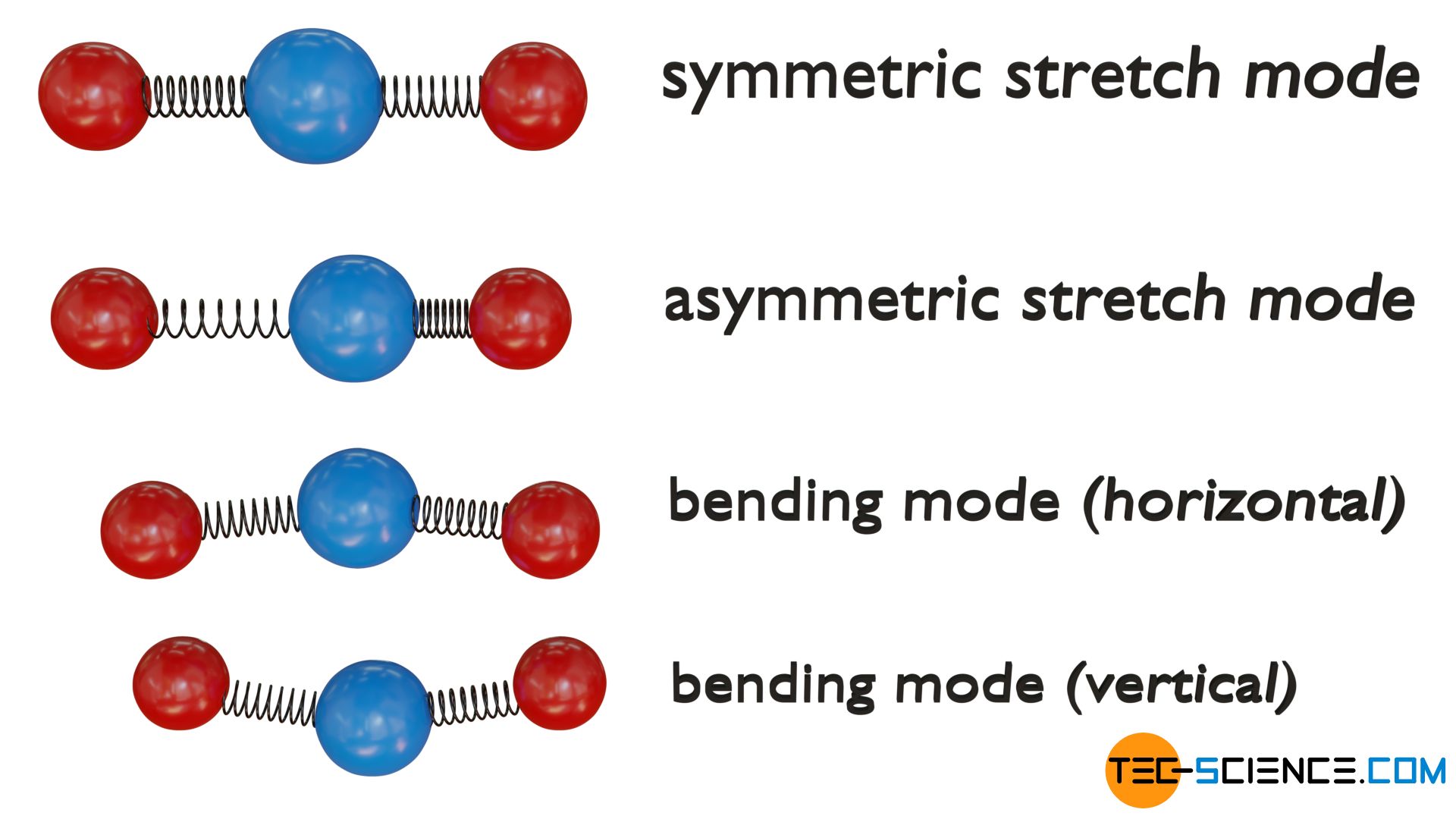
One normal mode of vibration results from the symmetrical stretching of the two outer atoms (red) along the molecular axis around the centrally located atom (blue). In addition, the molecule can also perform an asymmetric stretching motion by all three atoms vibrating along the molecular axis. The third and fourth vibrational mode result from a so-called bending mode (also referred to as scissoring). A distinction is made in which plane (vertical or horizontal) the vibrational bending motion takes place.
Triatomic non-linear molecules
For triatomic non-linear molecules, there are generally three vibrational degrees of freedom. At the one hand, again there is a symmetrical stretching of the outer atoms (red) along their molecular axis. At the other hand, again exists an asymmetrical stretching, where atoms vibrate phase-shifted. The third normal mode of vibration is again a bending (scissoring) mode, where the outer atoms vibrate in a kind of scissoring motion within the molecular plane (i.e. the bond angle oscillates around a resting position).
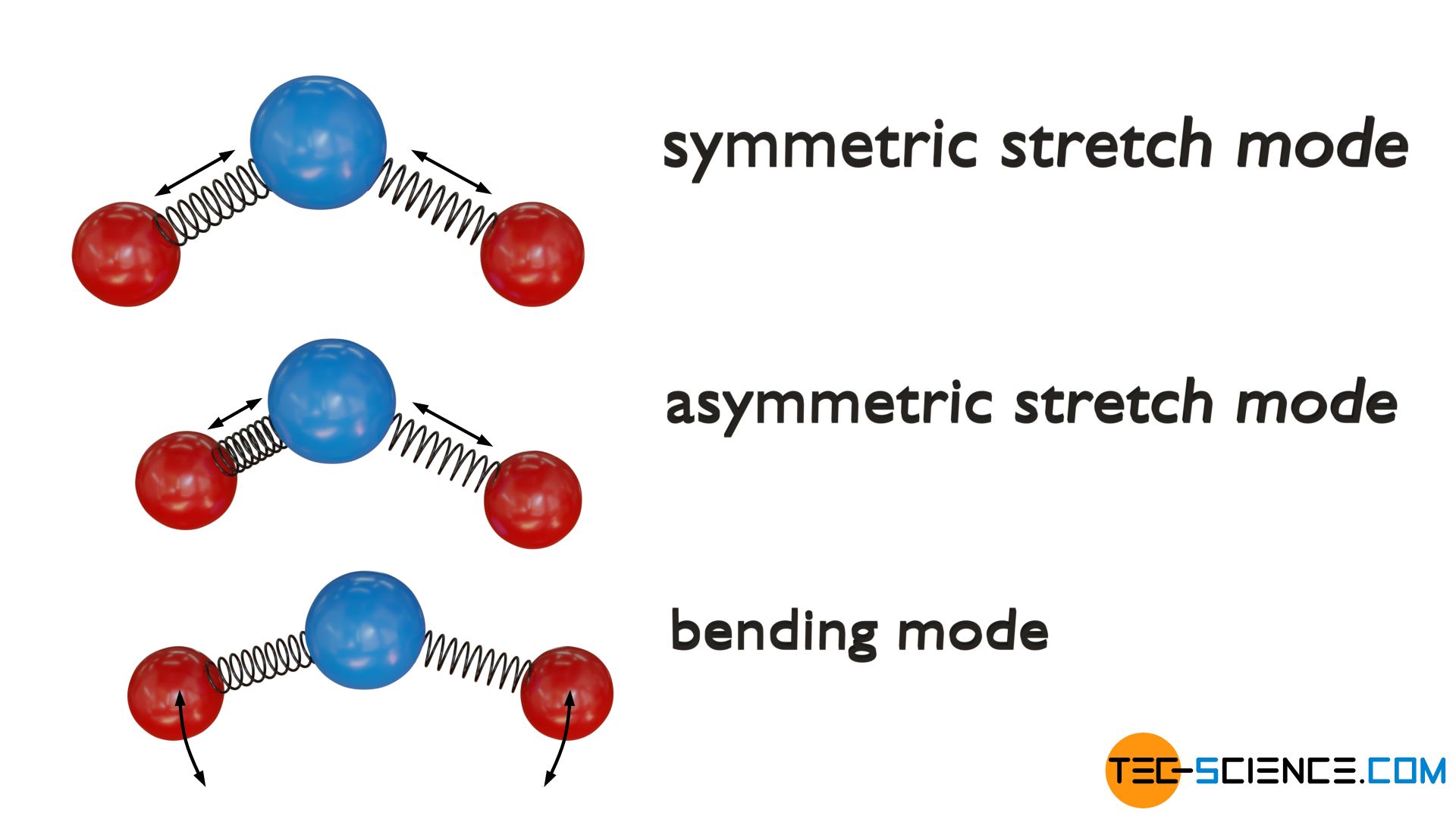
Determination of the number of normal modes of vibration
To determine the position of an atom within a molecule, one needs three coordinates (x-, y- and z-coordinates). A molecule with n atoms thus needs 3⋅n coordinates in total, by which it is then unambiguously defined at a certain point in time. This number of parameters corresponds to the total number of degrees of freedom ftot that a molecule has in principle:
\begin{align}
&\boxed{f_{tot} = 3 n} \\[5px]
\end{align}
These degrees of freedom can be divided into translation (ftrans), rotation (frot) and vibration (fvib):
\begin{align}
&f_{tot} = 3 n = f_{trans} + f_{rot} + f_{vib} \\[5px]
\end{align}
If the number of degrees of freedom of translation and the number of degrees of freedom of rotation are known, then the degrees of freedom of vibration (normal modes of vibration) can be determined as follows:
\begin{align}
\label{xx}
&\boxed{f_{vib} = 3 n – f_{trans} – f_{rot}} \\[5px]
\end{align}
Summary
It must be noted that for the number of degrees of freedom f that are relevant for the internal energy, the total degrees of freedom ftot are not essential, since from an energetic point of view the degrees of freedom of vibration must be counted twice!
If one divides the degrees of freedom between the translational motion (ftrans), the rotational motion (frot) and the vibrational motion (fvib), then the total number of degrees of freedom relevant for the internal energy is:
\begin{align}
\label{yy}
&\boxed{f = f_{trans} + f_{rot} + 2 \cdot f_{vib}} \\[5px]
\end{align}
If at this point equation (\ref{xx}) is used in equation (\ref{yy}), then the “energetic” degrees of freedom f can also be determined by the number of atoms n of a molecule:
\begin{align}
&f = f_{trans} + f_{rot} +2 \cdot \overbrace{ \left(3 n – f_{trans} – f_{rot} \right)}^{f_{vib} } \\[5px]
&\boxed{f =6n- f_{trans} – f_{rot}} \\[5px]
\end{align}
The table below shows the number of degrees of freedom for monatomic, diatomic and triatomic (non-linear) molecules.
| Molecule geometry | Translation ftrans | Rotation frot | Vibration fvib | Total f |
| monatomic | 3 | 0 | 0 (x 2) | 3 |
| diatomic | 3 | 2 | 1 (x 2) | 7 |
| triatomic (non-linear) | 3 | 3 | 3 (x 2) | 12 |
| triatomic (linear) | 3 | 2 | 4 (x 2) | 13 |