Learn more about the origin of the Celsius, Fahrenheit, and Kelvin temperature scales in this article.
Introduction
In everyday life, temperature is often understood as a quantity that expresses the property of a substance to be “hot” or “cold”. In fact, however, such a perception of hot or cold depends on various factors. Among other things, it depends on the thermal conductivity of the substance. For example, metal feels much cooler than wood at low temperatures due to its higher thermal conductivity, although both have the same temperature.

On the other hand, the human perception of temperature (human thermal response) depends on the “prehistory” of our skin with which we touch objects. For example, if we hold a hand in ice water and then put it in a pot of warm water, it feels much hotter than if we hold an uncooled hand in the pot with warm water.

Defining the temperature of a substance by the human sensation of being “hot” or “cold” therefore fails. For the determination of the temperature one uses therefore a different connection which is directly related to the temperature: the motion of the particles in a substance. As already explained in detail in the article “Temperature and particle motion“, the temperature of a substance is a measure of the kinetic energy of the particles contained in it (more precisely: a measure of the average kinetic energy of a particle).
Temperature is a measure of the kinetic energy of a particle in a substance!
This kinetic energy is also noticeable in the thermal expansion of substances. At high temperatures, the particles are very strongly in motion and thus occupy a larger space. In so-called liquid-in-glass-thermometers exactly this principle of thermal expansion is used to determine the temperature. A thermometric liquid* in glass tube (also called capillary tube) expands when heated and contracts when cooled. A calibrated scale can then be used to read off the respective temperature that led to the corresponding thermal expansion.
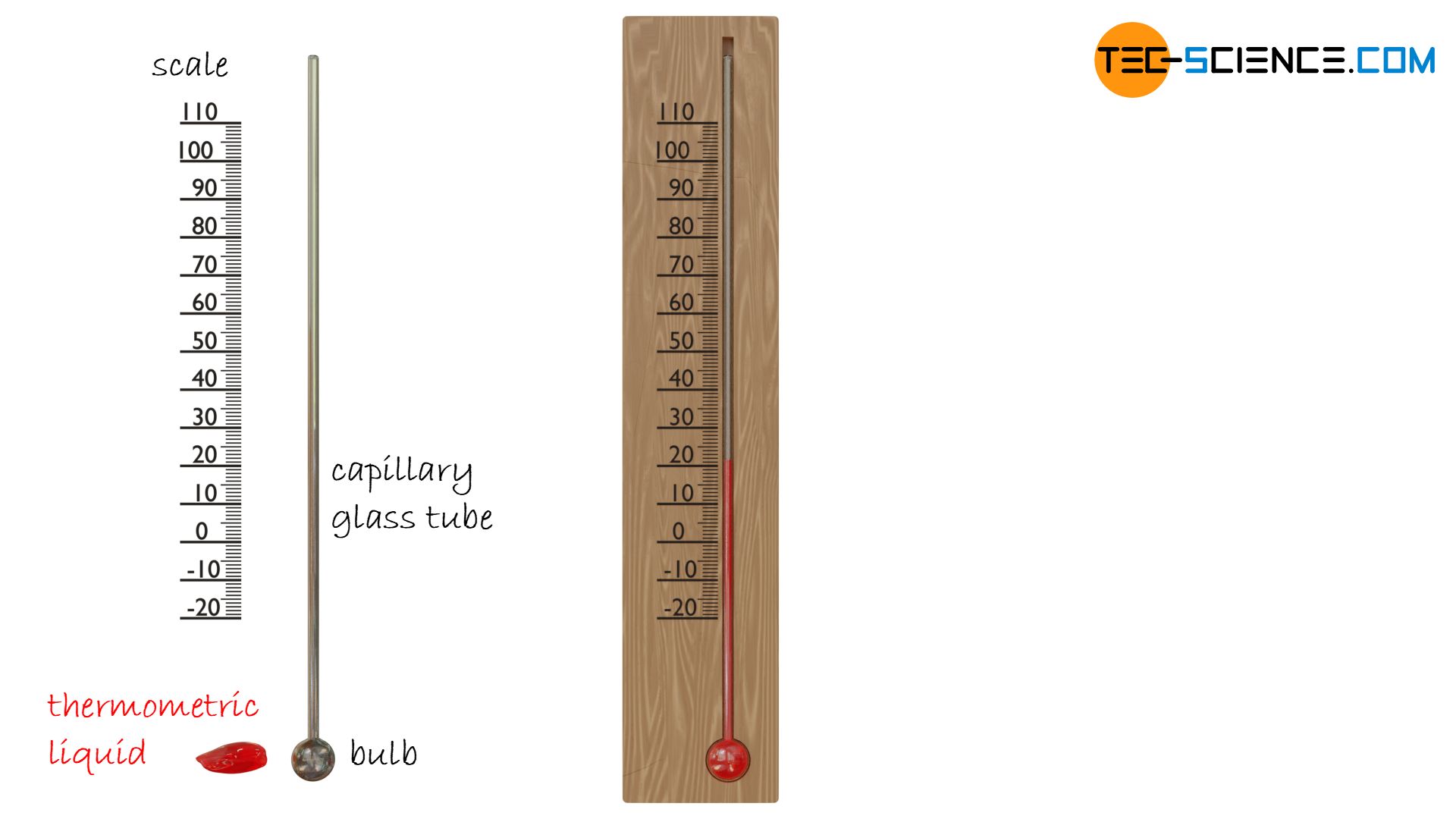
Depending on which reference points are used to determine the scale and thus to measure the temperature, there are three main temperature scales:
- Celsius scale
- Fahrenheit scale
- Kelvin scale
The different temperature scales are described in more detail in the following sections.
*) A liquid is considered thermometric if its volume changes uniformly with temperature and is therefore suitable for use in liquid-in-glass-thermometers. In the past, highly toxic mercury was used for this purpose; today, a coloured alcohol mixture is used (e.g. ethanol).
Celsius scale
In many countries it is common to measure the temperature of substances by means of the so-called Celsius scale. When the Swedish astronomer Anders Celsius defined the Celsius scale at the time, two reference points were used. One is the melting point of water and the other is its boiling point of water (both at an ambient pressure of 1 bar).

The melting point of water was arbitrarily defined as 0 (zero point), while the boiling point of water was given the value 100. All other temperatures can be obtained by interpolating or extrapolating this basic scale. The temperature values as they are obtained on the Celsius scale, are indicated with the unit degrees Celsius or centigrade (°C).
Fahrenheit scale
The German physicist Daniel Fahrenheit wanted to avoid negative temperature values on his temperature scale for everyday life. In the 17th century (well before Celsius), he therefore thought about the lowest possible temperature, which he could produce in his laboratory without technical aids.
He experimented with a cooling bath of water, ice, and ammonium chloride and was able to produce a minimum temperature of -17.8 °C. He used this temperature to determine the zero point of his Fahrenheit scale (0 °F). As a further reference point, Fahrenheit used the human body temperature and assigned the value 100 °F to it (37.8 °C) . The temperature values obtained on the Fahrenheit scale are denoted by the unit degrees Fahrenheit (°F).

The decisive handicap of the Fahrenheit scale was that the reference point defined by body temperature is not exactly reproducible. Everyone has a different body temperature depending on their daily form and physical activity.
For this reason, other reference points are used for today’s definition of the Fahrenheit scale, namely the freezing point of water at 32 °F (0°C) and the steam-point temperature of water at 212 °F (100 °C). Between the freezing point and boiling point of the water are therefore 180 degrees and not 100 degrees as with the Celsius scale. If the temperature in the Celsius scale changes by 1 degree, the temperature value in the Fahrenheit scale changes by 1.8 degrees. In addition, for the temperature value, the shift of the zero point for the freezing point of water must be taken into account (32°F). For the conversion of a temperature from the Celsius scale to the Fahrenheit scale, the following formula applies:
\begin{align}
&\boxed{ [°F] = [°C] \cdot 1,8 + 32} \\[5px]
\end{align}
Conversely, the following formula applies to the conversion of a given temperature in the unit degress Fahrenheit to degress Celsius:
\begin{align}
&\boxed{ [°C] = \frac{[°F] – 32}{1.8} } \\[5px]
\end{align}
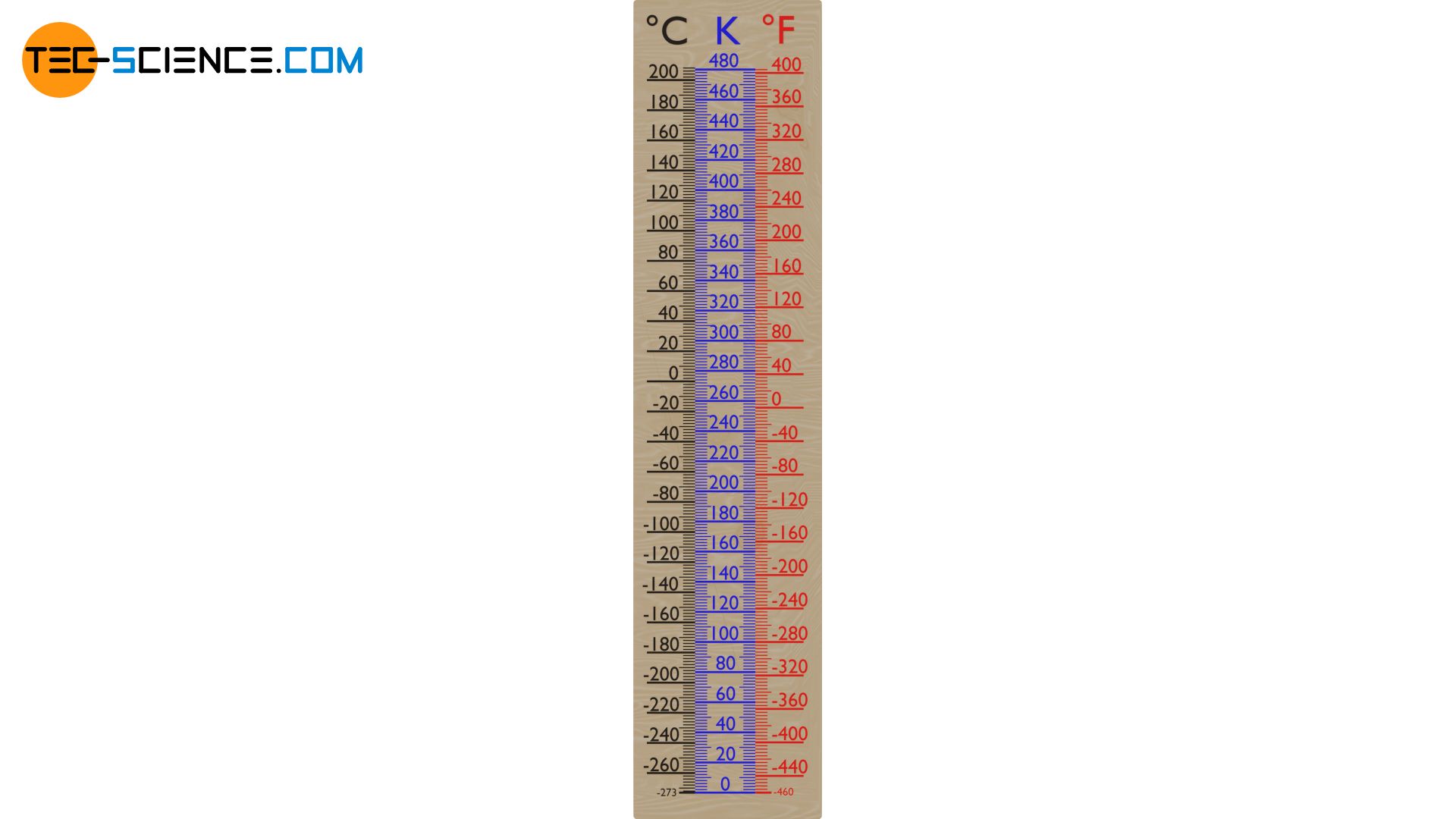
The figure below shows the comparison of the two temperature scales.

Kelvin scale
The Celsius scale and also the Fahrenheit scale are not very scientific due to the arbitrary determination of the reference points. Rather, a thermodynamical temperature scale should take into account the fact that temperature is a measure of particle motion. The temperature at which the particles no longer have any kinetic energy (i.e. are completely at rest) should therefore be used as the (absolute) zero point for a physically meaningful temperature scale.
Such an absolute “zero point” is used for the so-called Kelvin scale. The temperature at which the particles of a substance no longer have any motion is defined as the zero point. This temperature therefore represents the lowest possible temperature and is therefore also referred to as absolute zero.
On the Celsius scale absolute zero is at -273.15 °C or at -459,67 °F on the Fahrenheit scale and henceforth serves as the reference point for the Kelvin scale (zero point). Absolute zero is therefore denoted as 0 K (K: Kelvin). Like the Celsius scale, the Kelvin scale is divided into a total of 100 “degrees” between the melting point of water (273 K ≙ 0 °C) and boiling point of water (373 K ≙ 100 °C).
Absolute zero denotes the temperature at which the particles of a substance no longer have any kinetic energy, i.e. are completely at rest! Absolute zero is at -273.15 °C on the Celsius scale and -459.67 °F on the Fahrenheit scale!
The Kelvin scale is merely a shifted Celsius scale, with a scientifically determined zero point, that equals to the standstill of the particles contained in a substance. For the conversion of a temperature on the Celsius scale into the temperature on the Kelvin scale and vice versa, the following formulas apply:
\begin{align}
&\boxed{ [K] = [°C] + 273.15} \\[5px]
&\boxed{ [°C] = [K] – 273.15} \\[5px]
\end{align}
For the conversion of a temperature on the Fahrenheit scale to the temperature on the Kelvin scale and vice versa, the following formulas apply:
\begin{align}
&\boxed{ [K] = \frac{[°F] – 32}{1.8} + 273.15} \\[5px]
&\boxed{ [°F] = \left([K] – 273.15\right) \cdot 1.8 + 32 } \\[5px]
\end{align}
The figure below shows the comparison of the different temperature scales.
Experimental determination of absolute zero
In everyday life it is not really possible whithout further ado to cool substances so strongly that the temperature at absolute zero (on the Fahrenheit scale or the Celsius scale) could be determined directly. In addition, the atomic particles are not directly visible in order to be able to judge whether the point where the particles are motionless has actually been reached. In this section, therefore, an experiment for determining absolute zero is to be shown, which then leads to the implementation of the Kelvin scale.
In order to determine the temperature at absolute zero, at which the particles are completely motionless, the following considerations are made:
- If the temperature is to be a measure of the kinetic energy of the particles in a substance, then there must therefore be a lowest temperature at which the particles have no motion.
- For a real gas, this would mean that all gas particles contract to a smallest possible volume, since there is no particle movement.
- For an ideal gas whose particles are assumed to be mass points without spatial dimension, the volume at this lowest possible temperature would therefore be zero.
This means, that absolute zero can be determined by examining the laws between temperature and volume for an (approximately) ideal gas in more detail and then determining the temperature at which the volume should theoretically become infinitely small.

Experimental setup
Helium comes closest to an ideal gas, which is why it makes sense to study the relationship between temperature and volume of helium more closely. The examination of this temperature-volume relationship can be done with a glass tube containing helium (or in the simplest case air).
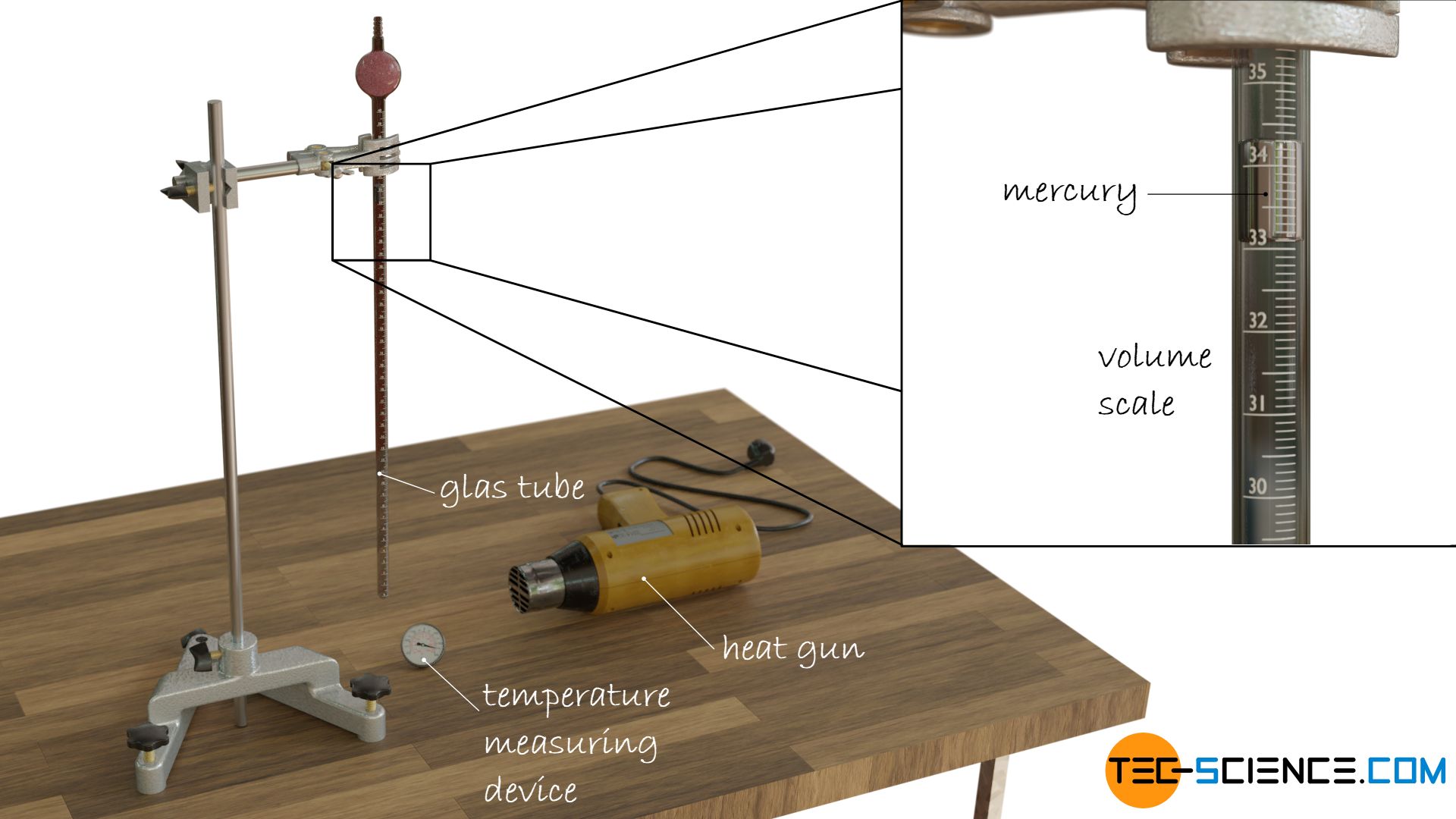
The glass tube is sealed with a droplet of mercury to prevent the gas from escaping while at the same time allowing it to expand and contract. The gas volume can therefore always adapt to the given temperature at a constant ambient pressure. The different temperatures can be adjusted for example with a heat gun. The volume which the gas occupies at a certain temperature can be read off directly from the scale on the glass tube.

In this experiment, it makes sense to first heat the gas to the maximum and to record the temperatures and volumina during cooling, as the cooling is much more uniform than the punctual heating with the heat gun. This ensures that the entire gas has a uniform temperature and does not only become hot here and there.
Evaluation
If the experiment is now carried out for different temperatures and the resulting temperature-volume relationship is graphically represented, a linear connection becomes apparent. This means that the volume increases continuously with an increase in temperature and decreases uniformly with a decrease in temperature. With the help of this regularity a prediction can now be made which lowest possible temperature can be expected at an infinitely small volume (which means at absolute zero).
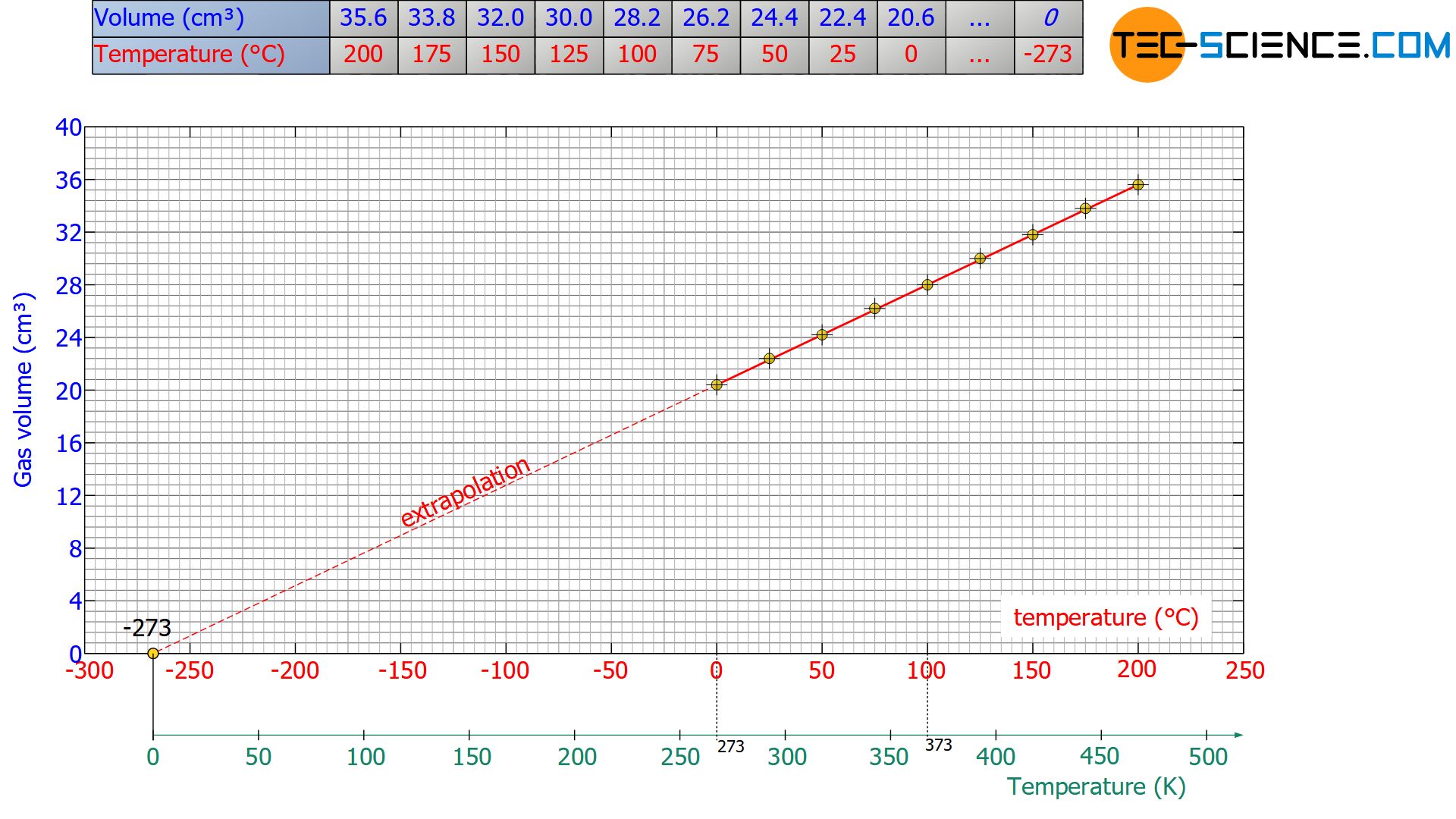
For this purpose, the straight line in the diagram is continued for ever smaller volumes (called Extrapolation) until finally the smallest possible volume of zero is reached at the point of intersection with the temperature axis. Consequently, the point of intersection with the temperature axis corresponds to absolute zero, which is at -273.15 °C on the Celsius scale and -459.67 °F on the Fahrenheit scale.
Note that the same temperature at absolute zero will also be obtained again and again when other types of gas are used. For this reason, this temperature value is called absolute zero, which applies to all substances in the world.
Note: Extrapolation is the determination of a value that lies outside a measured range. Hereby it is assumed without any reliable knowledge that the valid laws within the reliable range of the measured values can also be transferred to values outside. To what extent this is permissible must, however, be checked separately! Interpolation, on the other hand, is the determination of a value within a measured range that was not measured directly. Interpolation thus means the determination of a value between (lat. “inter”) two measured values.