The expansion of an ideal gas against a vacuum in an adiabatic system is an isothermal process!
In the article on the isentropic process it was already indicated that the often used term “adiabatic process” can be misleading in some situations and is generally not correct. To clarify this, the expansion of an ideal gas against a vacuum is considered in the following.
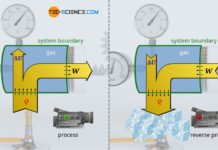
For this purpose, imagine a gas in a cylinder which is closed by a piston with negligible mass. The piston slides frictionless inside the cylinder. The piston is initially held in position by force. The cylinder is located in an evacuated chamber so that there is a vacuum on the outside of the piston. Cylinder and piston are assumed to be perfectly thermally insulated. It is therefore an adiabatic system. Now the piston is released and the gas expands against the vacuum.

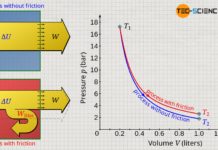
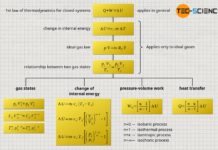
However, just because the cylinder and the piston form an adiabatic system, this does not mean that the derived laws of the supposed “adiabatic process” can be applied! According to these laws, the temperature should decrease during an expansion with increasing volume (T⋅Vκ-1=constant). However, this is not observed in the case considered, where the gas expands against the vacuum! The surprising result of this process shows up, if one takes a look at the first law of thermodynamics:
\begin{align}
\underbrace{W}_{=0} + \underbrace{Q}_{=0} = \Delta U = 0
\end{align}

Since it is an adiabatic system, by definition no heat is transferred (Q=0). Furthermore, the gas does not perform any work (W=0), because the gas expands against a vacuum. The gas does not have to exert any force to move the (massless!) piston. There is, so to speak, no counterpressure against which the gas has to push. Thus, the gas does not have to perform any work for the expansion of its volume. However, if no energy is transferred, neither as work nor as heat, the internal energy consequently remains constant (ΔU=0). Since the internal energy of an ideal gas is directly linked to the temperature (and this does not change), the free expansion of an ideal gas against a vacuum is therefore an isothermal process!
When an ideal gas expands in an adiabatic system against a vacuum, the temperature remains constant (isothermal process)!
Note: The fact that the temperature remains constant during expansion against the vacuum applies only to ideal gases. For real gases, on the other hand, a slight decrease in temperature will be observed. This phenomenon is referred to Joule-Thomson effect.
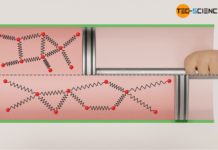
One can explain the isothermal expansion against a vaccum quite clearly. Imagine you are in a vacuum and you hold wildly flying particles in your hand. If you open your hand, the particles fly into the vacuum and are not slowed down by any other particles (since the piston is considered massless in the above example, you can also remove the piston and let the particles fly freely into the vacuum – this is the same situation). So the gas molecules keep their kinetic energy. Since the kinetic energy of the molecules is directly linked to the temperature, this means a constant temperature.
The adiabatic expansion of an ideal gas into a vacuum represents an isothermal process!
This example makes clear that thermodynamic processes in adiabatic systems cannot necessarily be described with the laws of isentropic processes. Therefore, in connection with the isentropic equations derived for this purpose, one should not speak of “adiabatic” processes. Because this suggests falsely that for all adiabatic systems these equations could be used. However, the expansion against a vacuum disproves exactly this.
Of course, the question arises under which condition a thermodynamic process of an adiabatic system can actually be described by the derived isentropic equations. The answer to this question can be found in the article Reversibility of thermodynamic processes (entropy).