Learn more about polytropic thermodynamic processes in closed systems in this article.
Particular processes shown in a volume-pressure diagram
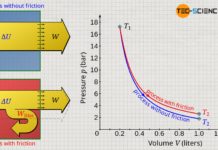
The figure below shows the course of the pressure as a function of the volume for an isobaric, isochoric, isothermal and isentropic process. All processes take place starting from an initial volume V1. The pressure curves show both an expansion and a compression. For the isentropic process, an isentropic index of air with κ=1.4 was used.
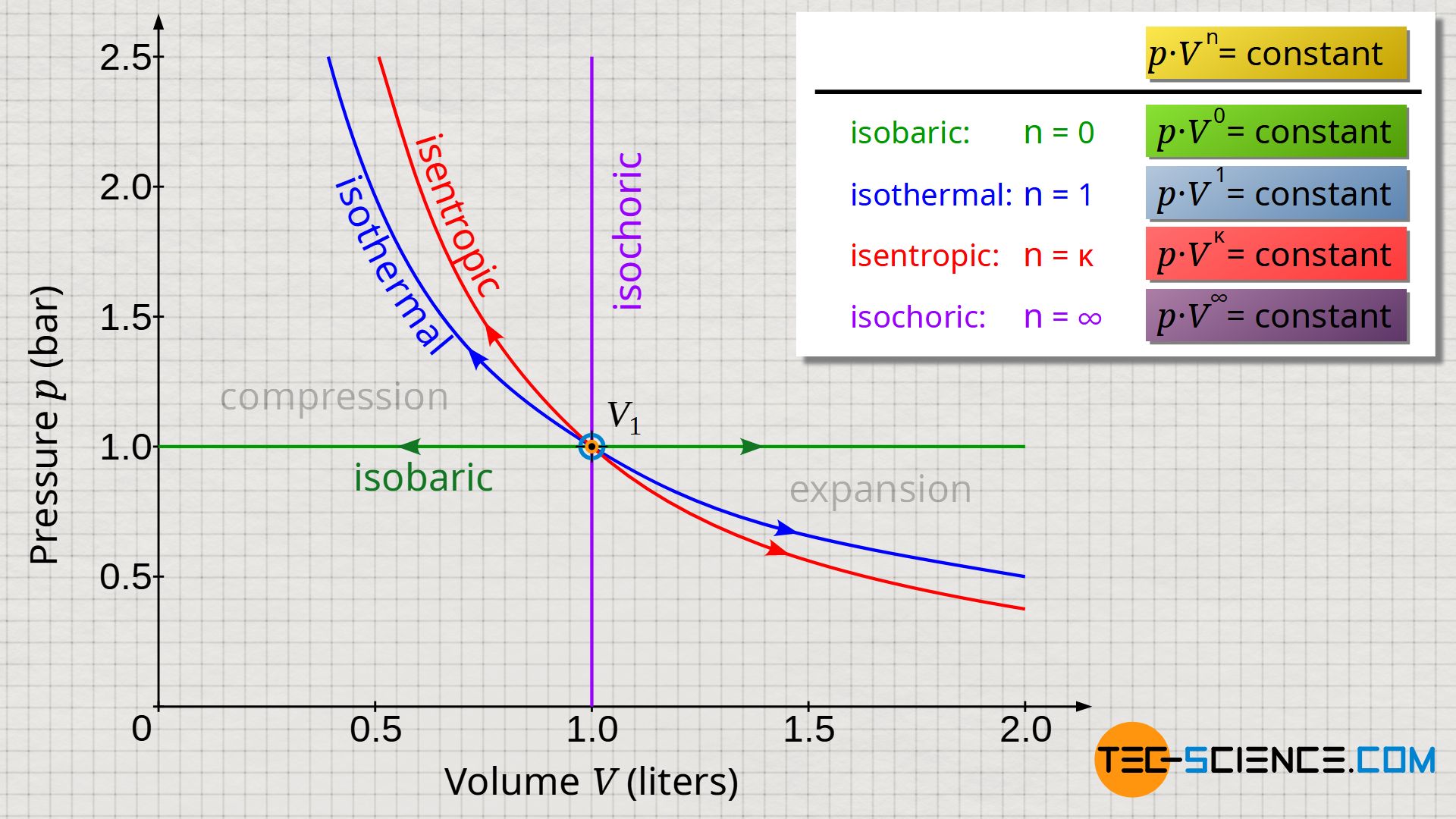
Although the shown thermodynamic processes appear at first glance to be very different from one another, a closer look reveals common characteristics. These become clear when one takes a closer look at the pressure as a function of the volume:
\begin{alignat}{3}
\text{isobaric process: } ~~~ &p=\text{constant} &&~~~~~~ \Rightarrow ~~~ &&& { p~V^0 =\text{constant}} \\[5px]
\text{isothermal process: } ~~~ &p\sim {1\over V} &&~~~~~~ \Rightarrow ~~~ &&& { p~V^1 =\text{constant}} \\[5px]
\text{isentropic process: } ~~~ &p\sim {1\over V^{\kappa}} &&~~~~~~ \Rightarrow ~~~ &&& { p~V^{\kappa} =\text{constant}} \\[5px]
\text{isochoric process: } ~~~ &V=\text{constant} &&~~~~~~ \Rightarrow ~~~ &&& { p~V^{\infty} =\text{constant}} \\[5px]
\label{8858}
\end{alignat}
From the comparison it is clear that the entire processes shown can be generalized to obey the relation p⋅Vn=constant, where a very specific exponent n can be found for each thermodynamic process:
\begin{align}
\label{3445}
& \boxed{p~V^{n} =\text{constant}} ~~~~~~ {p_1~V_1^n}={p_2~V_2^n} \\[5px]
\end{align}
Note: Why n=∞ holds for the isochoric process becomes clear if one first solves equation (\ref{3445}) with respects to the volume V and then sets n=∞:
\begin{align}
p~V^n=\text{const.} ~~~\Rightarrow ~~~
V ={\left(\text{const.} \over p \right)^{1 \over n}}
={\text{const.} \over p^{1 \over n}}
\overset{n=\infty}={\text{const.} \over \underbrace{p^0}_{=1}}
=\text{constant!} \nonumber \\[5px]
\end{align}
Polytropic equations
Not only the relationship between pressure and volume, but also the relationship between temperature and volume or temperature and pressure can be generalized. These relationships can be derived using the ideal gas law and equation (\ref{3445}). Thus, all special processes (isobaric, isochoric, isothermal and isentropic) treated so far can be reduced to obey the following equations:
\begin{align}
\label{2716}
\boxed{p~V^n=\text{constant}} &~~\Rightarrow~~ \boxed{p_1~V_1^n=p_2~V_2^n} \\[5px]
\label{4375}
\boxed{T~V^{n-1}=\text{constant}} &~~\Rightarrow~~ \boxed{T_1~V_1^{n-1}=T_2~V_2^{n-1}} \\[5px]
\label{7991}
\boxed{T^n~p^{1-n}=\text{constant}} &~~\Rightarrow~~ \boxed{T_1^n~p_1^{1-n}=T_2^n~p_2^{1-n}} \\[5px]
\text{ mit: }~~ &n=0 ~~~\text{isobaric process} \nonumber \\
&n=1 ~~~\text{isothermal process} \nonumber \\
&n=\kappa ~~~\text{isentropic process} \nonumber \\
&n=\infty ~~~\text{isochoric process} \nonumber \\
\end{align}
However, the exponent n is not limited to the special cases such as isobaric, isothermal, isentropic and isothermal. In principle, the exponent can be chosen arbitrarily! The choice depends decisively on which exponent can best describe the thermodynamic process in reality. After all, most thermodynamic processes in reality never run exactly isobaric, isothermal, isentropic or isochoric. The diagram below shows for selected values of n the respective pressure curves. Depending on which curve comes closest to the actual thermodynamic process, the corresponding exponent would then have to be chosen. In principle, negative exponents are also feasible!
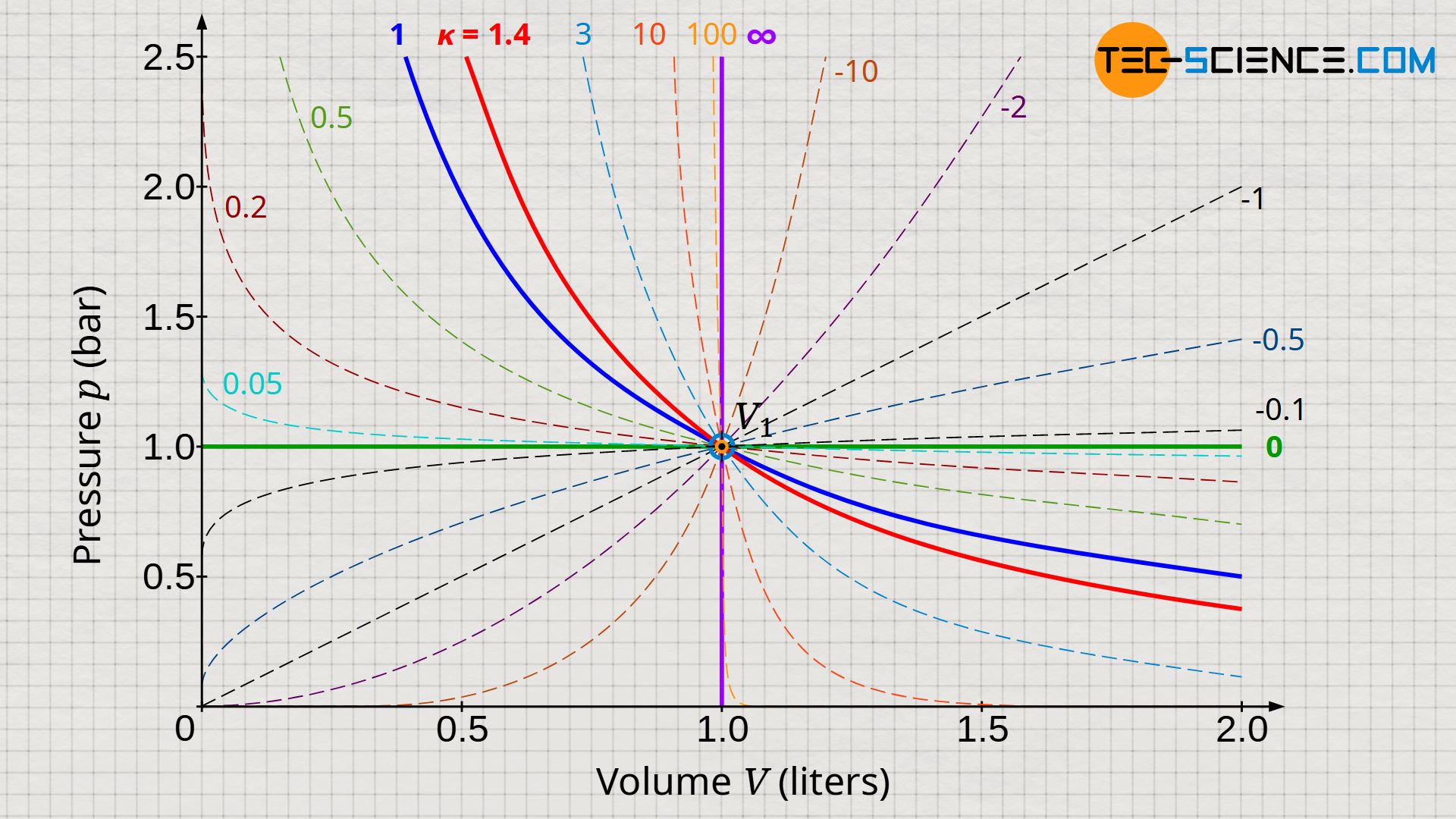
Note that ultimately all the curves shown belong to the same set of curves described by the equation (\ref{2716}).
Since equations (\ref{2716}) to (\ref{7991}) can be used to describe a large number of thermodynamic processes (including special cases), the processes behind these equations are commonly referred to as polytropic processes (“poly”=many). The exponent n is therefore also called polytropic index. The isobaric, isothermal, isentropic and isochoric processes are therefore only to be regarded as special cases of a generally polytropic process!
Pressure-volume Work and heat
Besides the equations (\ref{2716}) to (\ref{7991}) describing the state of a gas by state variables, general formulas for calculating the process quantities such as pressure-volume work Wv and transferred heat Q, as well as for the change of the internal energy ΔU can also be found for polytropic processes. Due to their complexity, the derivation of the formulas given below will be discussed in more detail in the linked article. In this article only the formulas are discussed in more detail:
\begin{alignat}{2}
\label{4862}
&\boxed{W_\text{V} = \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~\left(T_2-T_1 \right)}& &= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[\left(T_2\over T_1\right)-1 \right] \\[5px]
&&&= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&= \left[{{\kappa-1} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[20px]
\label{5451}
&\boxed{Q = \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~\left(T_2-T_1 \right)}& &= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[\left(T_2\over T_1\right)-1 \right] \\[5px]
&&&= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&= \left[{{n-\kappa} \over {n-1}}\right] ~c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[20px]
\label{9277}
&\boxed{\Delta U = c_\text{v}~m~\left(T_2-T_1 \right)}& &= c_\text{v}~m~T_1~\left[{T_2 \over T_1}-1 \right] \\[5px]
&&&= c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{n-1}}-1 \right] \\[5px]
&&&=c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-n} \over n}}-1 \right] \\[5px]
\end{alignat}
Note that the isentropic index κ in the above equations is to be understood only as the ratio of the heat capacities (κ=cp/cv). Therefore, one should not be deceived into thinking that these equations are valid only for an isentropic process, just because there is an isentropic index κ! In principle, these equations describe any polytropic process, the special cases like isobaric, isochoric, isothermal and isentropic of course included!
However, care must be taken at this point for the special case of the isothermal process with a polytropic index of n=1, since in this case the denominator in the equations would become zero. From a mathematical point of view, there is no solution for such a case. With sufficient accuracy, however, a polytropic index close to one can be chosen as an alternative, for example n=0.999.
Relationship between change in internal energy and work/heat
If we look more closely at equations (\ref{4862}) and (\ref{5451}), we notice that the term cv⋅m⋅(T2-T1) just corresponds to the change in internal energy ΔU. Thus, the pressure-volume work Wv and the transferred heat Q can also be given as a function of the change of the internal energy ΔU:
\begin{align}
\label{6763}
&\boxed{W_V= \left[{{\kappa-1} \over {n-1}}\right] ~\Delta U} \\[5px]
&\boxed{Q= \left[{{n-\kappa} \over {n-1}}\right] ~\Delta U} \\[5px]
\end{align}
It is now obvious that transferred work and heat for a given polytropic process are always in a constant ratio:
\begin{align}
\require{cancel}
\label{3657}
{W_V \over Q} = {{\left[{{\kappa-1} \over \bcancel{n-1}}\right]~\bcancel{\Delta U}} \over {\left[{{n-\kappa} \over \bcancel{n-1}}\right]~\bcancel{\Delta U}}}
= { {\kappa-1} \over {n-\kappa} } \\[5px]
\end{align}
\begin{align}
\label{3285}
\boxed{{ W_V \over Q } = { {\kappa-1} \over {n-\kappa} }} \\[5px]
\end{align}
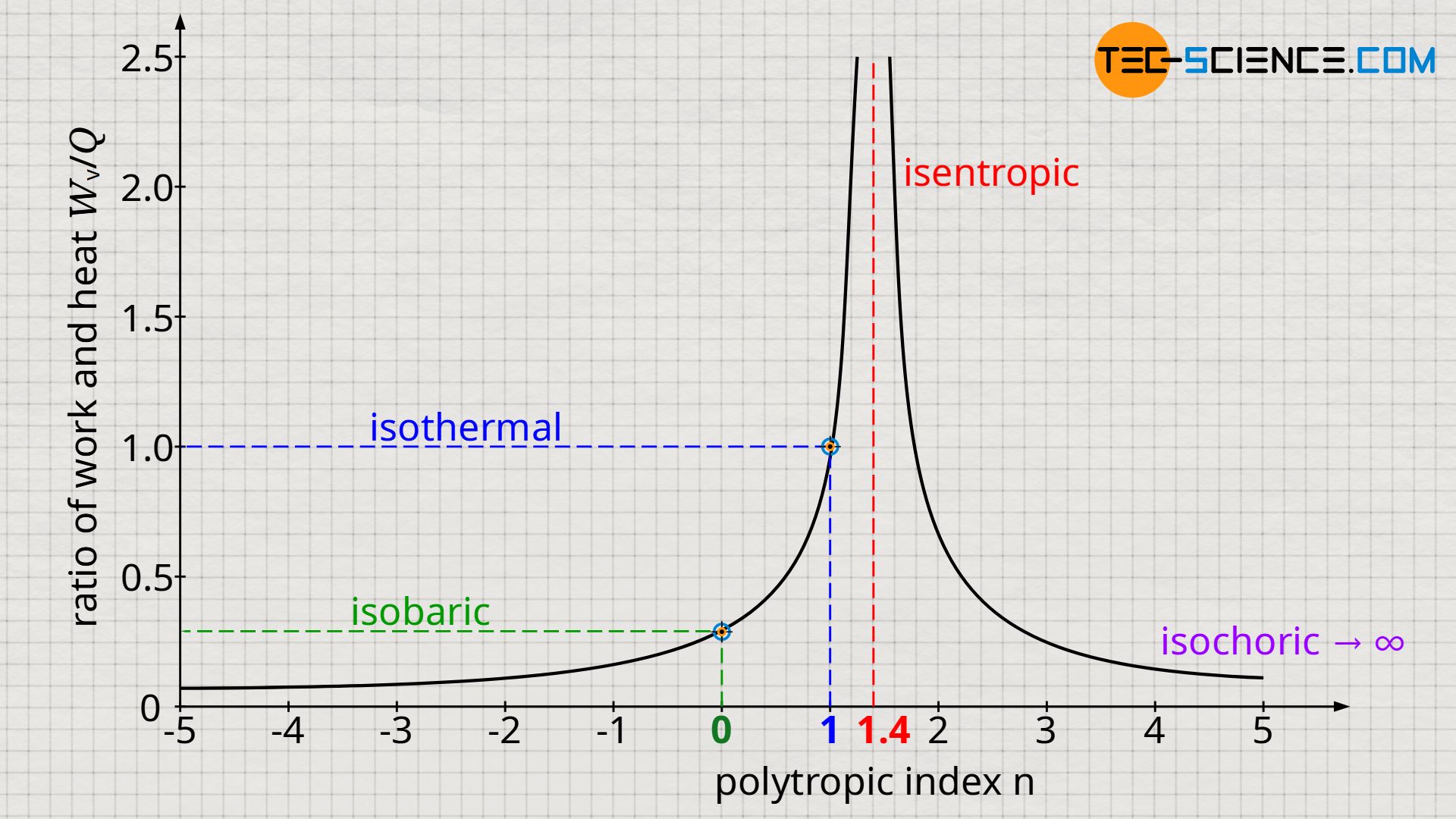
The diagram below shows for an isentropic index of κ=1.4 the (positive) ratio of work and heat as a function of the polytropic index.
Isobaric process
For any isobaric process with n=0 and κ=1.4 (for air), the quotient of work and heat is (-)0.286. This means that for an isobaric expansion, 28.6% of the supplied heat is converted into (pressure-volume) work. The remaining 71.4% of heat energy benefits the internal energy. This result is independent of the pressure, volume or temperature at which the isobaric process takes place! Only the type of gas influences the efficiency with which the supplied heat is converted into work. For example, the share of the converted pressure-volume work can be increased to 40.1% if helium with an isentropic index of κ=1.67 is used instead of air!
Isentropic process
For a thermodynamic process described with a polytropic index of n<κ, the result of equation (\ref{3285}) is negative. This means that, mathematically speaking, work and heat have opposite signs. Thus, heat must be added to the gas (Q>0) while the gas expands (Wv<0). For the reverse case, heat must be released by the gas (Q<0) when the gas is compressed (Wv>0).
For the special case of a process with an isentropic index n→κ, the denominator in the equation (\ref{3285}) approaches more and more zero. This means that the transferred heat (in relation to the pressure-volume work) decreases and is finally zero at n=κ. For this special case, the isentropic process is obtained, which is exactly characterized by this fact that no heat is transferred.
\begin{align}
{ W_V \over Q } = { {\kappa-1} \over {n-\kappa} } \overset{n\rightarrow\kappa}= \infty
~~~\Rightarrow~~~Q= {W_V\over \infty} = 0
\nonumber \\[5px]
\end{align}
Isochoric process
On the other hand, for a thermodynamic process with an isentropic index n→∞, the denominator in the equation (\ref{3285}) approaches more and more infinity. This means that the transferred work (in relation to the transferred heat) decreases and is finally zero at n=∞. For this special case, the isochoric process is obtained, which is exactly characterized by this fact that no work is transferred.
\begin{align}
{ W_V \over Q } = { {\kappa-1} \over {n-\kappa} } \overset{n\rightarrow\infty}= 0
~~~\Rightarrow~~~W_V= {Q \cdot 0} = 0
\nonumber \\[5px]
\end{align}
Isothermal process
Another special case is shown by the equation (\ref{3285}) for n=1. In this case, the magnitude of the transferred work is as large as the magnitude of the transferred heat (with opposite signs). Thus, the heat absorbed by the gas is completely converted into work and released by the gas. Therefore, the internal energy of the gas is neither reduced nor increased, i.e. it remains constant. For an ideal gas this means that temperature remains constant. The special case n=1 thus corresponds to the isothermal process, which is exactly characterized by this fact that the temperature remains constant.
\begin{align}
{ W_V \over Q } = { {\kappa-1} \over {n-\kappa} } \overset{n\rightarrow 1}= -1
~~~\Rightarrow~~~W_V= -Q
\nonumber \\[5px]
\end{align}
Importance of polytropic processes in real life
As already explained in detail, the polytropic equations (\ref{2716}) to (\ref{7991}) can describe, depending on the polytropic index n, all special cases considered so far, such as the isobaric (n=0), isothermal (n=1), isentropic (n=κ) and isochoric process (n=∞). Also, a variety of other thermodynamic processes can be described depending on the chosen polytropic index. Nevertheless, not all processes obey these polytropic equations (e.g. the expansion process described in this article, in which a weight is lifted by a lever via a rack and pinion).
Nevertheless, polytropic processes are of great technical importance, especially in the range between n=1 (isothermal process) and n=κ (isentropic process). This is because many thermodynamic processes occur between these limiting cases. This becomes clear if one takes a closer look at these thermodynamic processes.
As an example, the compression of air inside an air pump is considered with the outlet valve kept closed. If the compression is carried out (infinitely) slowly, any increase in temperature is immediately compensated by heat dissipation to the surroundings. Thus, the temperature of the gas will not increase during such a slow process. Therefore, an (infinitely) slow thermodynamic process represents an isothermal process – at least the described process for compressing air with the help of an air pump.

However, if the compression of air is performed (infinitely) fast, the temperature increase cannot be compensated, since the system has no time to transfer any significant amount of heat to the surroundings. Therefore, an (infinitely) fast thermodynamic process represents an isentropic process.
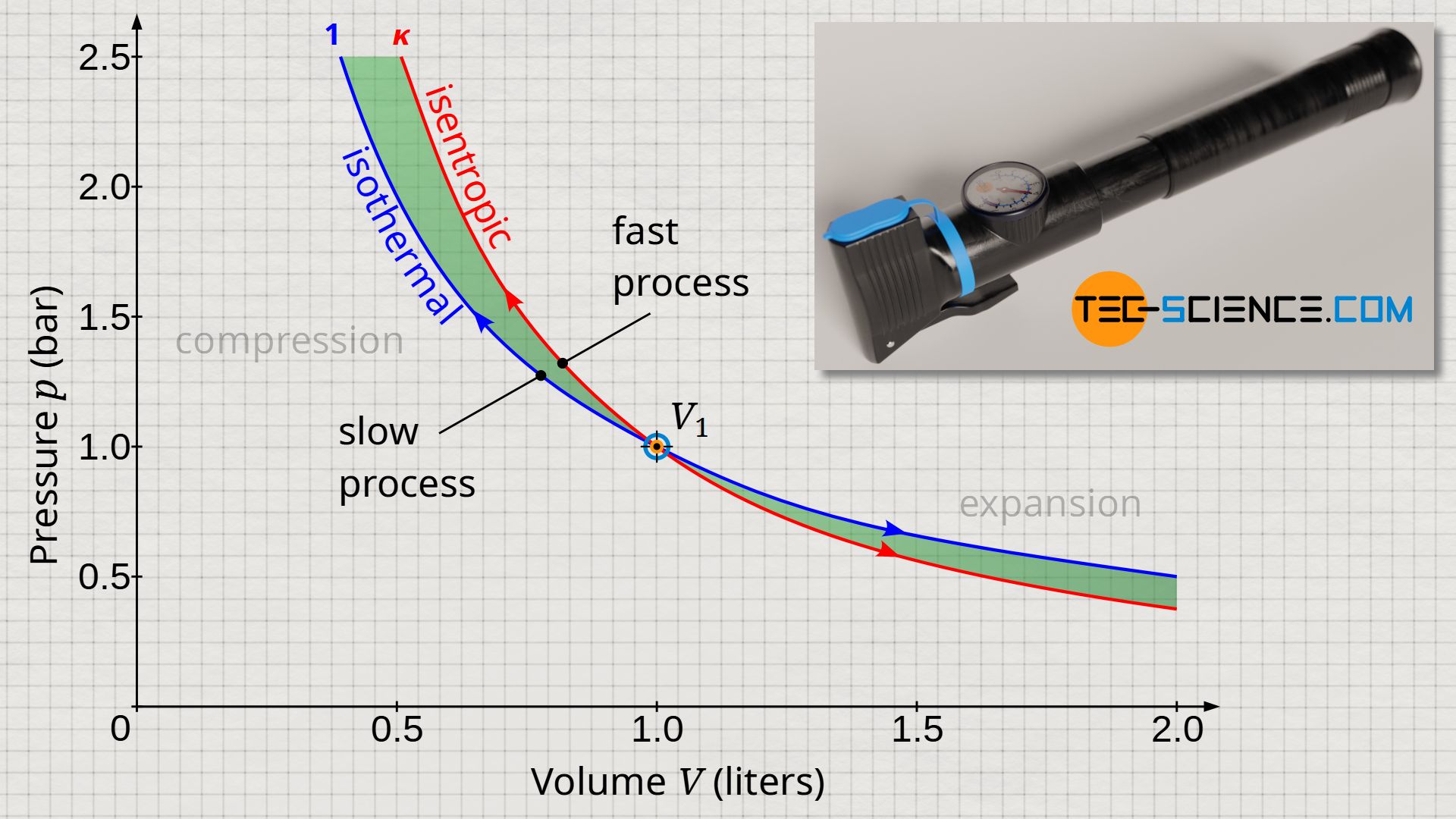
In reality, however, a thermodynamic process can be neither infinitely slow nor infinitely fast, so that the actual process will run between these two limiting cases. Consequently, the polytropic index will have a value between 1 (isothermal process) and κ (isentropic process). Often, the term polytropic process is limited to exactly those thermodynamic processes whose polytropic indices lie in the range between n=1 and n=κ. Especially in cases where energy is dissipated, the thermodynamic process is often approximated by such a polytropic process. More information on this can also be found in the article Dissipative thermodynamic processes in adiabatic systems.