Dissipation is the (partial) conversion of a certain form of energy into thermal energy that cannot be fully converted back into the original form of energy.
Definition
Dissipation of energy means that when one form of energy (e.g. potential energy) is converted into another (e.g. kinetic energy), it can no longer be completely converted back into its original form. Friction, for example, is a typical dissipative process in which mechanical energy is converted into thermal energy and cannot be completely converted back into mechanical energy. Mechanical energy has thus been (partially) dissipated into thermal energy. The dissipation of energy is thus a irreversible process.
Example of dissipation of energy by friction
An example of a dissipative process is the rolling of a toy car along a roadway. The track starts from a certain height and then goes downhill. The track then goes into a loop and then leads back uphill to the starting point. The toy car now rolls down from the starting point. During the ride, potential energy is converted into kinetic energy and vice versa. Without friction, the toy car would return to its original height after the ride and arrive at the starting point.

In reality, friction occurs both at the wheels of the vehicle (sliding friction) and between the vehicle and the air (drag). In this case, the car an the surroundings heat up at those points where friction occurs. The car no longer reaches its original height. The difference between the potential energy at the beginning and at the end corresponds to the energy dissipated by friction. This amount of energy can no longer be converted back into kinetic or potential energy to bring the car back to its initial position. Thus, the original potential energy of the car has been partially dissipated into thermal energy.
Dissipation of energy in thermodynamics
Expansion and compression of a gas in a cylinder
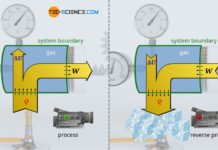
Many thermodynamic processes also involve friction, which results in dissipation of energy. As an example of such a process, let us consider a cylinder which is closed by a piston. The piston is now pressed into the cylinder by force. Such a compression of the gas, however, does not only increase the pressure. Work is obviously done on the gas as a result of the force applied during compression. The mechanical work supplied to the system is converted into thermal energy, or more generally, into internal energy of the gas. This explains not only the increase in pressure, but also the increase in temperature during compression (see also the article Why do pressure and temperature increase during the compression of a gas?)

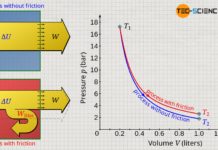
Ideally, the work of compression stored as internal energy can be completely converted back into mechanical energy (adiabatic system assumed). In the process, the high gas pressure in the cylinder will push the piston back to its original position while releasing the same amount of work. After expansion, pressure and temperature drop back to the original value before compression.
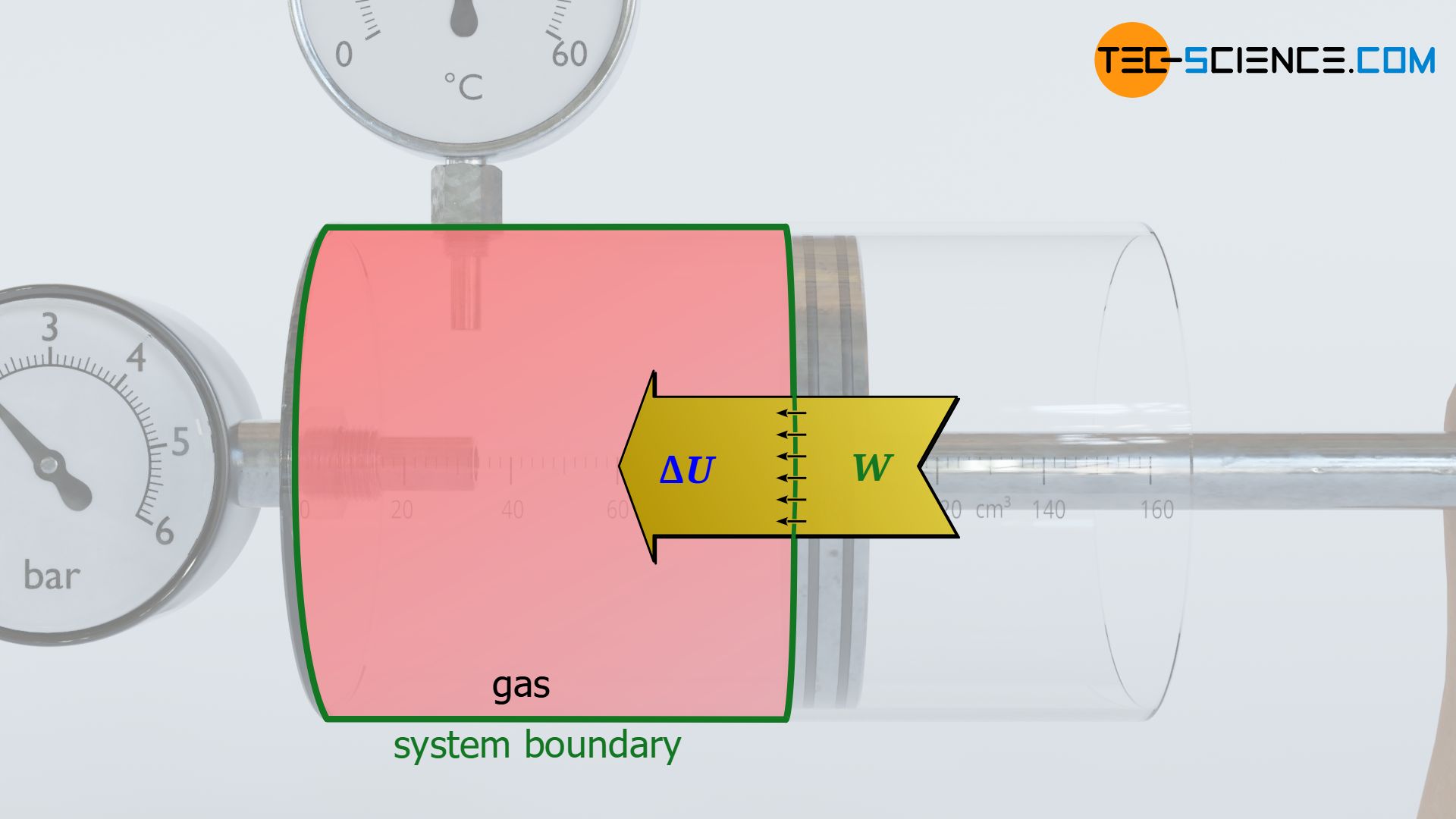
In reality, however, friction will occur between the cylinder wall and the piston during both compression and expansion. The work done on the gas during compression is greater than the work done by the gas during expansion. The difference between the two amounts of energy corresponds to the dissipated energy. This dissipated energy remains in the system as internal energy. The increased internal energy, in turn, is directly noticeable in a higher temperature of the gas compared to the frictionless ideal case (see also the article Internal energy of ideal gases).
Dissipation of energy by a stirrer
Another example of a dissipative process is a stirrer placed inside the cylinder. Depending on how viscous the gas behaves, more or less force is required to drive the stirrer. This is ultimately due to the “friction” between the stirrer and the gas. The work required to drive the stirrer is completely dissipated into internal energy. Thus, stirring is noticeable by an increase in the temperature of the gas.
This phenomenon is also known from everyday life, for example when whipping cream with a mixer. The cream whipped will have a higher temperature. One often hears the following explanation in this context: “Friction between the mixer and the cream generates heat”. In technical terms, however, this is not correct, because in thermodynamics, heat means an energy transfer as a result of a temperature difference (see article Heat and thermodynamic equilibrium). In the considered case, however, the cause of the energy transfer is not a temperature difference, but is of a mechanical nature.

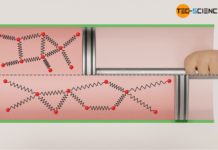
This fact can also be clearly understood with the particle model of matter. The rotating blades of the stirrer collide with the gas molecules in the cylinder. This gives the molecules additional momentum (kinetic energy) and they fly away at a higher speeds. Thus, mechanical energy is transferred from the stirrer to the gas molecules. The situation can be compared to a tennis player who is hitting a tennis ball with his racket. The tennis ball is accelerated by the racket moving at high speed. In the analogous way, the gas molecules will also be accelerated by the blades of the stirrer.
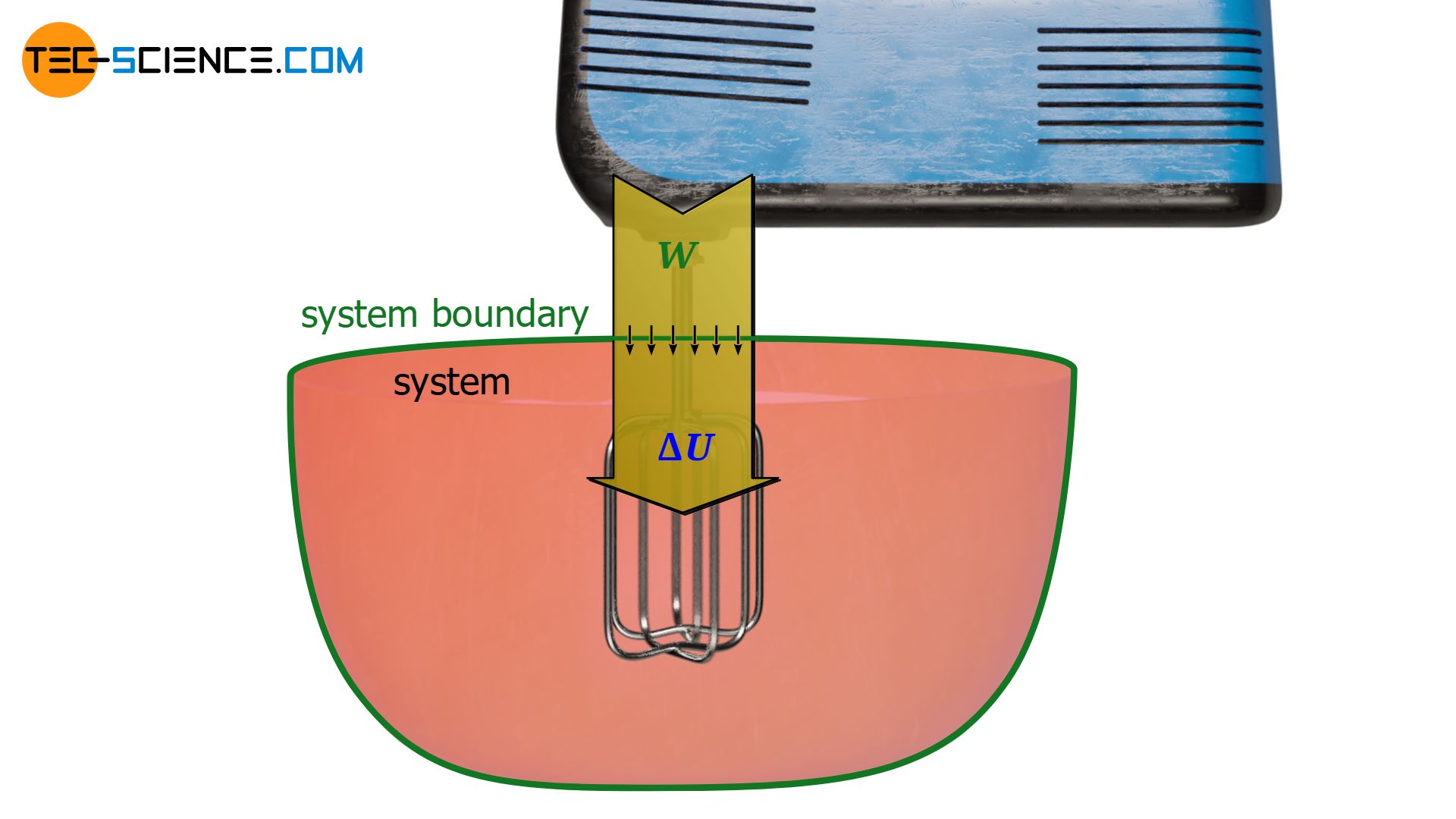
Furthermore, this analogy of the tennis player makes it clear that in the considered case of the stirrer, energy is obviously dissipated even if the gas is regarded as an ideal gas in which no friction exists in the classical sense. For even then, the ordered motion of the stirrer is transformed into a random thermal motion of the gas molecules and cannot be transformed back (i.e., the gas molecules are not able to set the stirrer into an ordered rotational motion at a later time and to release the energy brought into the system by the stirring). Thus, friction in the classical sense does not always have to be present for a dissipative process.

Dissipation of electrical energy
Not only mechanical energy, but also electrical energy can be dissipated into internal energy. In principle, this is already the case with the mixer, provided that the mixer is regarded as part of the system. In this case, electrical energy is transferred across the system boundary and is dissipated into internal energy. Note that to judge which form of energy is dissipated, only the form of energy transported across the system boundary is relevant.
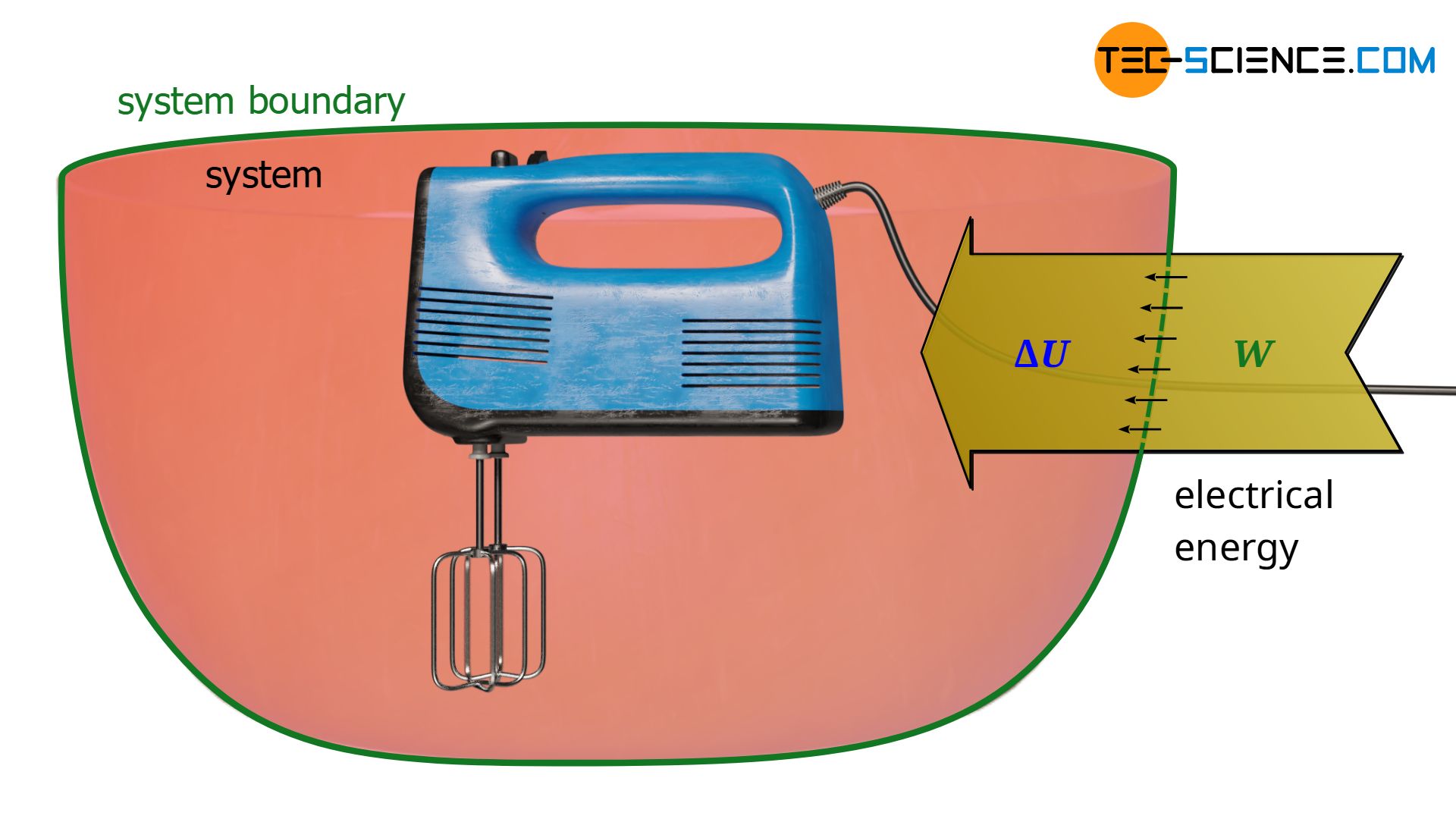
Instead of an electrically driven stirrer, we now consider a heating coil. In this case, electrical energy is also transferred across the system boundary, which is dissipated into internal energy, resulting in an increase in temperature. So, from a thermodynamic point of view there is no difference whether the electrical energy ist dissipated by a mixer or a heating coil. In the thermodynamic sense, therefore, the gas is not heated in the true sense of the word, but electrical energy is dissipated as a form of work!
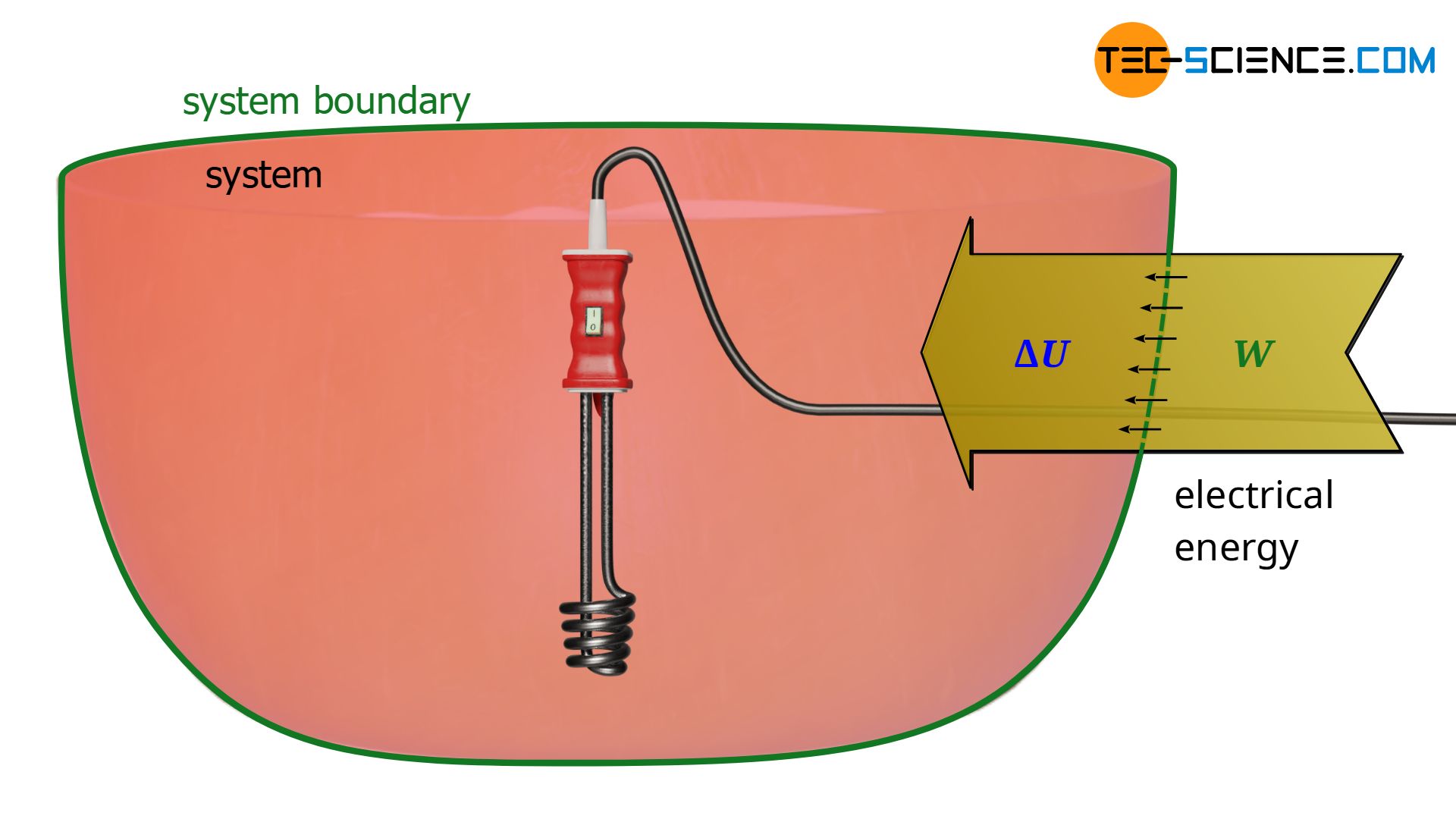
In this case, electrical energy crosses the system boundary. Whether this energy is used to operate a heating coil or a stirrer is no longer important after the energy has flowed across the system boundary. If, on the other hand, the heating coils were installed outside the system, then we would be talking about heat that is supplied to the system (energy transfer across the boundary due to a temperature difference). In the present case, however, the electrical energy is only transformed into thermal energy inside the system and dissipated into internal energy.