The pressure-volume work (displacement work) is the work don on the gas or by the gas due to the acting gas pressure during a change in volume.
Heat engines and heat pumps
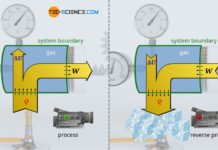
Gases play an important role in thermodynamics. In internal combustion engines, for example, they convert heat into work. The temperature of the gaseous fuel-air mixture rises due to heat released during the combustion of the fuel. This leads to an increase in pressure in the cylinder, which pushes the piston down and drives the crankshaft. From the point of view of the gas, therefore, heat is supplied to the gas on the one hand, while on the other hand work is done by the gas. The gas thus converts heat into work. For this reason, internal combustion engines are also generally referred to as heat engines.

The reverse energy conversion, i.e. the conversion of work into heat for heating purposes, on the other hand, takes place in so-called heat pumps. The principle of a heat pump can be illustrated using an air pump. If the outlet valve is closed during pumping, not only does the pressure rise very sharply, but an increase in temperature can also be observed due to the work done on the gas during compression. From the point of view of the gas, therefore, work is done on to the gas on the one hand, while the gas in turn releases heat. The gas therefore converts work into heat.

Thus, gases play a central role in both heat engines and heat pumps. Therefore, the release or absorption of work during the change of state of a gas will be discussed in more detail in this article. This ultimately leads to the concept of pressure-volume work.
Changes of state in volume-pressure diagrams
In the following, we will consider a horizontally standing cylinder which is closed by a movable piston. The piston slides friction-free inside the cylinder. With the piston rod, which is designed as a rack, a weight is lifted via a gear wheel and a lever. Consequently, it is a closed thermodynamic system with the cylinder walls and the piston surface as the system boundary.

To be able to lift the weight, the pressure in the cylinder must be increased. This is done by heating the gas with a Bunsen burner, which increases the temperature of the gas and thus raises the pressure. When the pressure is finally high enough, the gas begins to push out the piston with a certain force.
Let us now look at the process from the point of view of the gas. On the one hand, heat is supplied to the gas and, on the other hand, work ist done by the gas in order to lift the weight. During the lifting of the weight, the gas obviously passes through different thermodynamic states characterized by different volumes, pressures and temperatures. In order to illustrate such thermodynamic changes of state of the gas, they are often represented in a volume-pressure diagram.
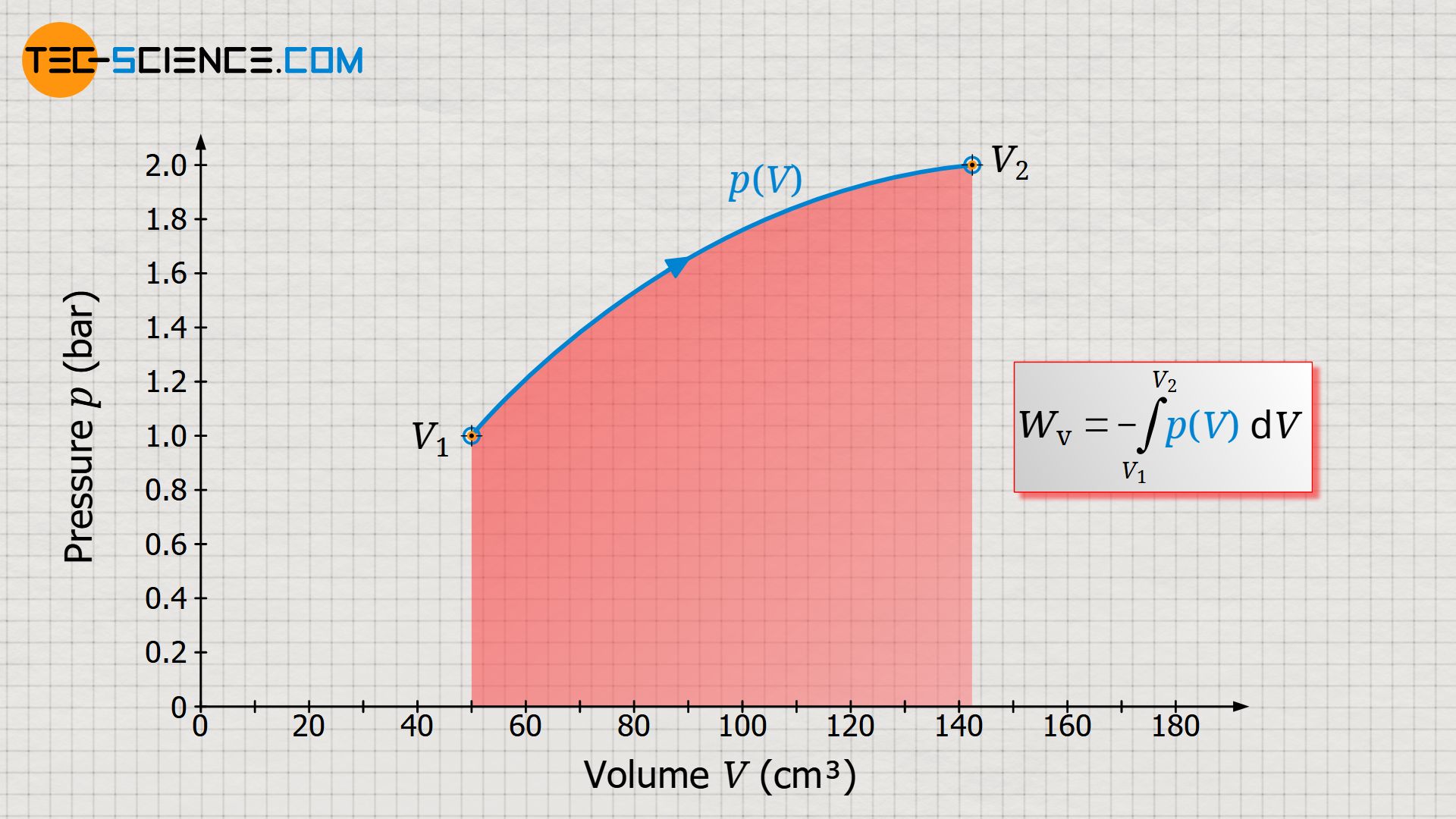
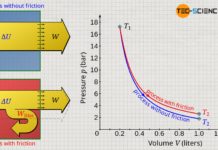
To explain the pressure curve: At the beginning of the process, the gas pressure is in equilibrium with the ambient air pressure of 1 bar, so that the gas in the cylinder also has a pressure of 1 bar. In this initial state, the gas has a volume of 50 ml, and the temperature is 20 °C. The gas is now heated. Due to the absorbed heat and the associated temperature increase, the pressure now increases. At the same time, this causes the piston to move and the weight to be lifted. The gas volume increases as a result. Due to the increasing leverage ratio during lifting, the gas must subsequently apply more and more force on the piston surface in order to lift the weight further. The gas pressure must therefore increase steadily as the volume continues to increase. Finally, the weight is completely lifted at a gas volume of 142.5 ml. The pressure in this final state is around 2 bar at a gas temperature of 1413 °C.
In a volume-pressure diagram not only the different thermodynamic stats of the process can be shown, but it also offers the ability to determine the work done by the gas clearly. This work results from the area under the curve! This is also shown by a short comparison of the units which are plotted on the axes and which have to be multiplied with each other when calculating the area:
\begin{align}
&\text{[Fläche]} = [p] \cdot [V] = \frac{\text{N}}{\text{m²}} \cdot \text{m³} = \text{N} \cdot \text{m} = \text{J} = \text{[Arbeit]} \\[5px]
\end{align}
Of course, an area under the curve as the work done by the gas (or on the gas!) only result if the gas volume changes during the thermodynamic process. For this reason, the work done by the gas or on the gas is also referred to as pressure-volume work Wv (also called displacement work). Mathematically, this pressure-volume work can be determined as the integral of the pressure function p(V) within the boundaries between initial volume V1 and final volume V2 (a detailed derivation of the following formula can be found in the article Derivation of the pressure-volume work (displacement work)):
\begin{align}
\boxed{W_\text{v} = – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V} ~~~\text{pressure-volume work (displacement work)} \\[5px]
\end{align}
Note that the pressure-volume work in an expansion (volume increase) is done by the gas, i.e. the gas transfers work across the system boundary to the surroundings. Whereas in the case of compression (volume reduction), the pressure-volume work is done on the gas, i.e. the surroundings transfer work across the system boundary to the gas.
The pressure-volume work (displacement work) is the work don on the gas or by the gas due to the acting gas pressure during a change in volume.
Pressure-volume work as a path-dependent quantity
If the initial and final state of a gas in a thermodynamic process are known, it is imperative to know the exact course of the state curve in the volume-pressure diagram in order to determine the pressure-volume work. This is because, depending on the path, there are different areas under the curves and thus different pressure-volume work.
In comparison to the process described above, two further thermodynamic processes are shown in the p(V)-diagram. Although initial and final states are obviously identical, however, different areas under the curves and thus different pressure-volume work result. Compared to process (1), the pressure-volume work is higher for process (2) and lower for process (3). Thus, the weight cannot be raised as much in process (2) as in the first process. In process (3), on the other hand, the weight can be raised higher due to the greater pressure-volume work.
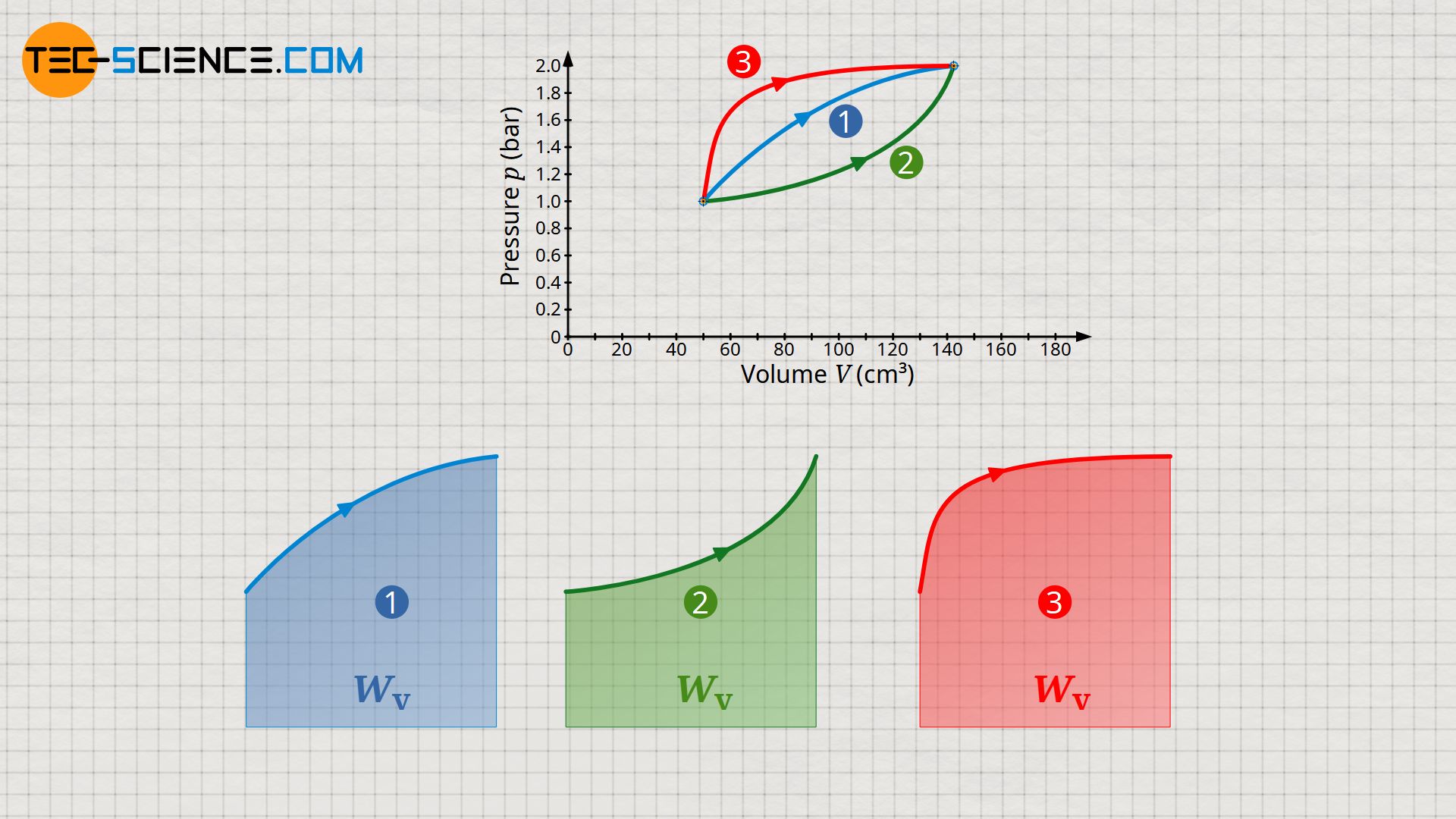
The pressure-volume work thus depends to a decisive extent on how the process proceeds exactly between the initial and final state. The pressure-volume work as a path-dependent quantity is a typical process variable. Further information can be found in the article The process quantities: Heat and work.
The pressure-volume work is a process quantity and results in a volume-pressure diagram from the area under the state curve (path-dependent)!
Pressure-volume work ≠ useful work
One could prematurely think that the pressure-volume work corresponds to the work which the system effectively performs on the weight in order to lift it. In general, however, this is not the case for two reasons!
On the one hand, it must be kept in mind that the gas must not only push the piston due to the attached load (gravitational potential energy of the weight), but also displace the piston against the ambient air pressure outside the cylinder, which acts on the piston from the opposite side. The work performed on the weight corresponds to the benefit intended by the entire apparatus and is therefore also called useful work, while the displacement of the piston against the (static) ambient air pressure is called flow work.
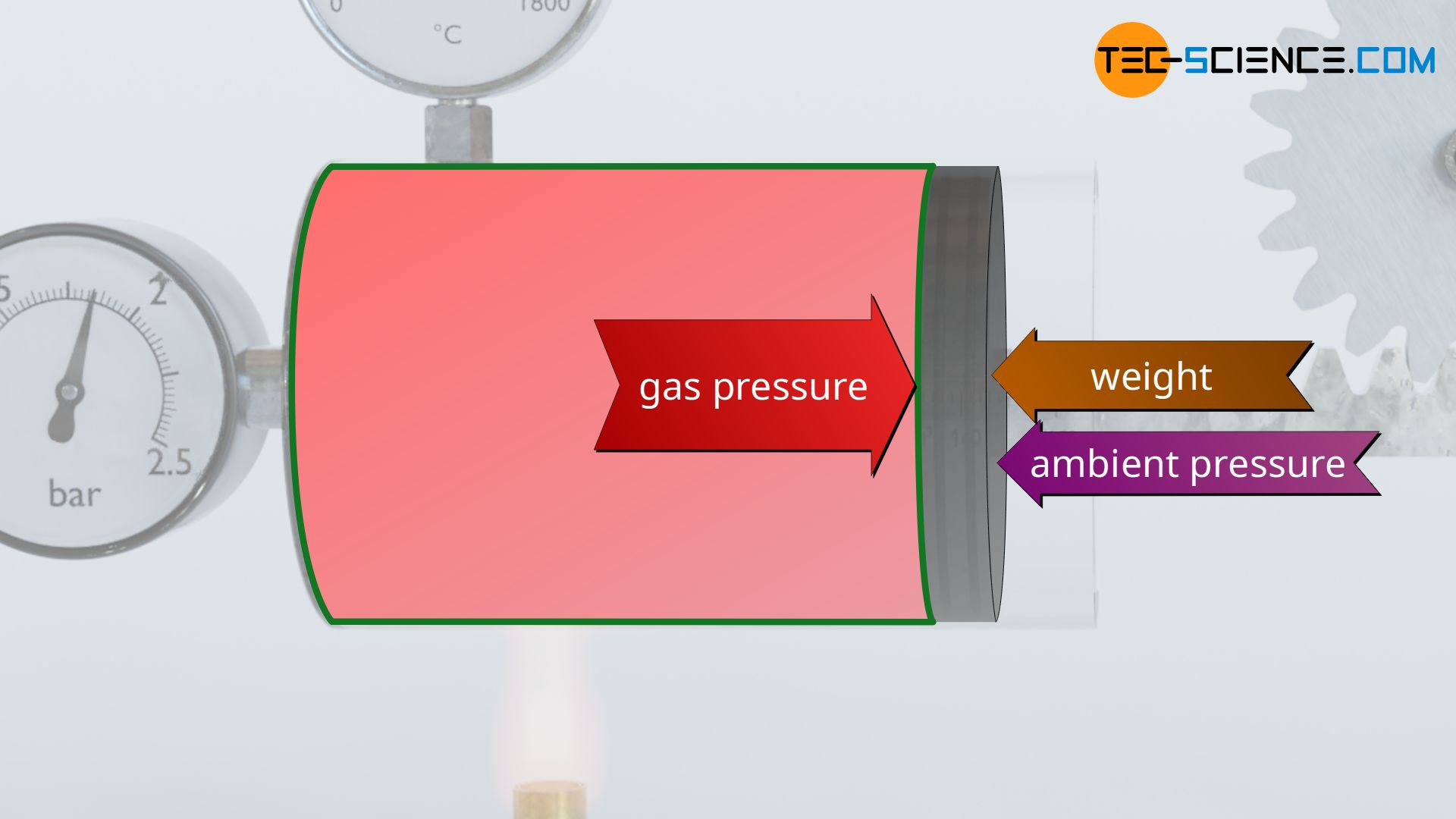
On the other hand, it must be kept in mind that processes do not run without friction in reality. In the present case, friction occur between the piston and the cylinder wall. The gas must therefore also push the piston against the acting friction. The gas must therefore perform additional work to compensate for friction (dissipation of energy). The dissipation of energy will be discussed in more detail in a separate article.
The pressure-volume work Wv, which is done by the gas to increase its volume (area under the p(V)-curve!), is therefore generally the sum of useful work Wu, static-pressure work Ws and friction work Wf:
\begin{align}
\boxed{W_\text{v} = W_\text{u} + W_\text{s} + W_\text{f} } \\[5px]
\end{align}
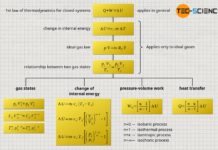
First law of thermodynamics
During the conversion of energy described above, does the gas convert all the absorbed heat Q to into mechanical work W?
To answer this question, let us consider the situation immediately after the load has been fully lifted. It becomes clear that the gas is obviously only able to hold the weight in position if the gas pressure is high to generate the necessary force. The required pressure is achieved by a strong increase in temperature. The temperature of the gas must therefore necessarily be higher after the weight has been lifted than at the beginning. However, this in turn means a change in the internal energy of the gas, which for an ideal gas is directly linked to the temperature change. In this specific case, an increase in the internal energy.
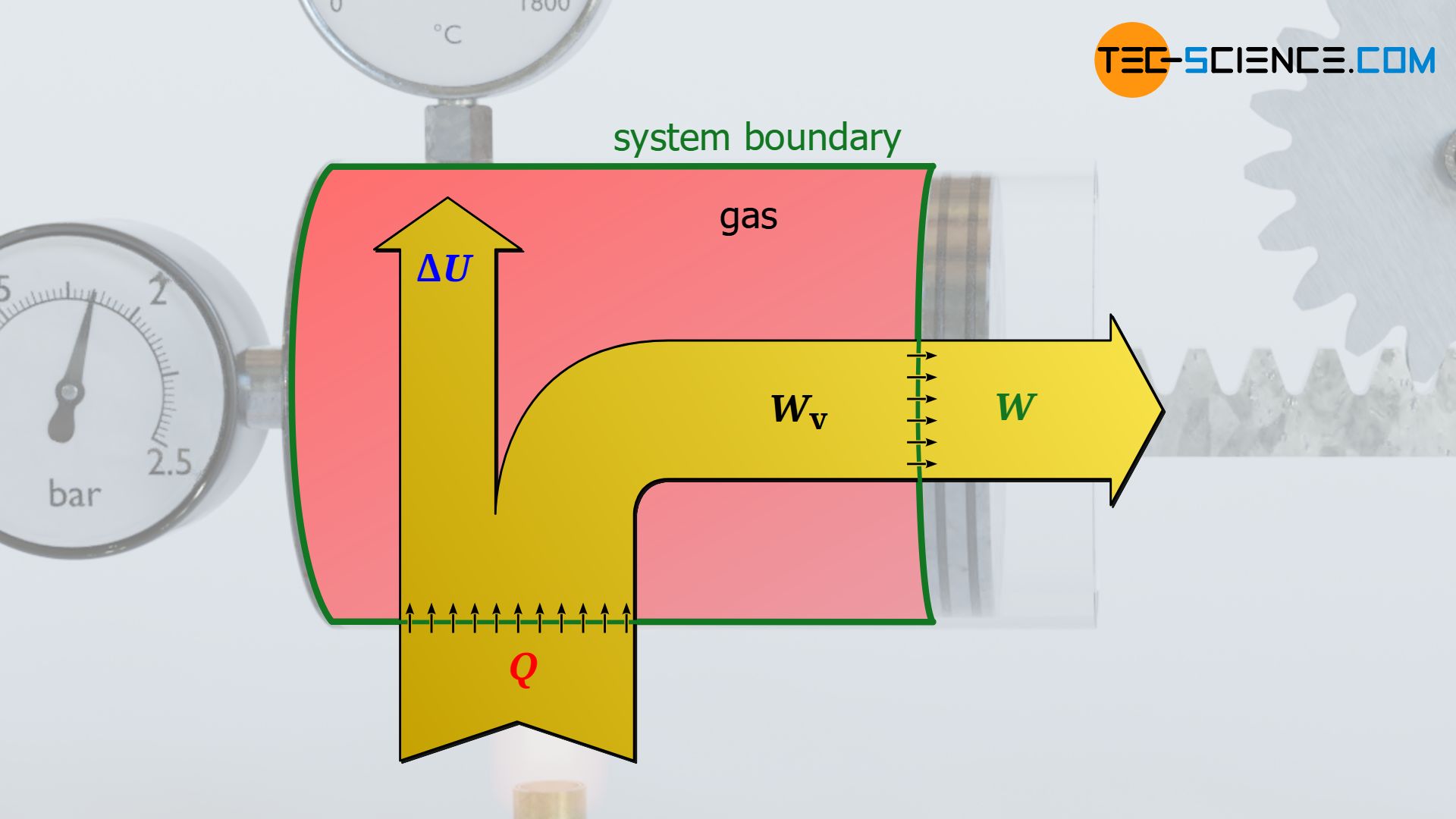
The absorbed heat Q>0 by the gas is therefore not completely converted into work W<0 and released by the gas. A certain part of the supplied heat remains as internal energy ΔU>0 in the system and provides for the necessary temperature increase (for the convention of the positive and negative signs see article Internal energy & first law of thermodynamics)! The relationship between these energies is described by the first law of thermodynamics:
\begin{align}
\label{wg}
&\boxed{W + Q = \Delta U} ~~~\text{first law of thermodynamics for a closed system}\\[5px]
\end{align}
Note that the heat Q and work W given in the first law of thermodynamics are always to be understood as energy transferred across the system boundary (process variables!). These transferred energies cause a change in the internal energy ΔU of the system (state variable!). The work transferred across the system boundary is also called boundary work. Only for a frictionless case, i.e. without dissipation of energy, the boundary work W corresponds to the pressure-volume work Wv of the gas.