In this article, learn more about the calculation of pressure, volume, work and heat in an isothermal process in a closed system.
A change of state of a gas in which the temperature does not change is also called an isothermal process. This means that the same temperature applies to all the states through which the gas passes between the initial and final state.
How to achieve an isothermal process
An isothermal process in a closed system takes place, for example, when any temperature changes are immediately compensated by absorbing or releasing heat. If an air pump is compressed while the outlet valve is kept closed, the gas inside is compressed. This is normally associated with an increase in temperature. However, if the gas is cooled at the same time, the temperature can be kept constant during compression. Conversely, in an isothermal expansion, heat must be supplied to the gas to counteract the temperature decrease that would otherwise occur.

An isothermal process can approximately be realized by allowing the expansion or compression of the gas to proceed so slowly that any temperature changes that would otherwise occur are very quickly compensated for by the surroundings (through releasing heat by the gas or through absorbing heat by the gas). Just imagine compressing the air of an air pump not within a few seconds, but over several minutes or hours. In this case, there will be no noticeable increase in temperature during compression and the process can be considered quasi-isothermal.
Illustration in the volume-pressure diagram
If a gas is isothermally compressed at a temperature T, the gas volume will decrease from V1 to V2. This is associated with an increase in pressure from p1 to p2. According to the ideal gas law, pressure and volume behave inversely proportional in an isothermal process. The exact relationship between pressure p and volume V is obtained by solving the ideal gas law with respect to the pressure p:
\begin{align}
\label{eq:6942}
&p~V = R_\text{s} \cdot m \cdot T ~~~\text{ideal gas law}\\[5px]
\label{pv}
&\boxed{p ={ \underbrace{R_\text{s}~m~T}_{=\text{constant}} \cdot {1 \over V}}} ~\Rightarrow~ p \sim {1 \over V}
\end{align}
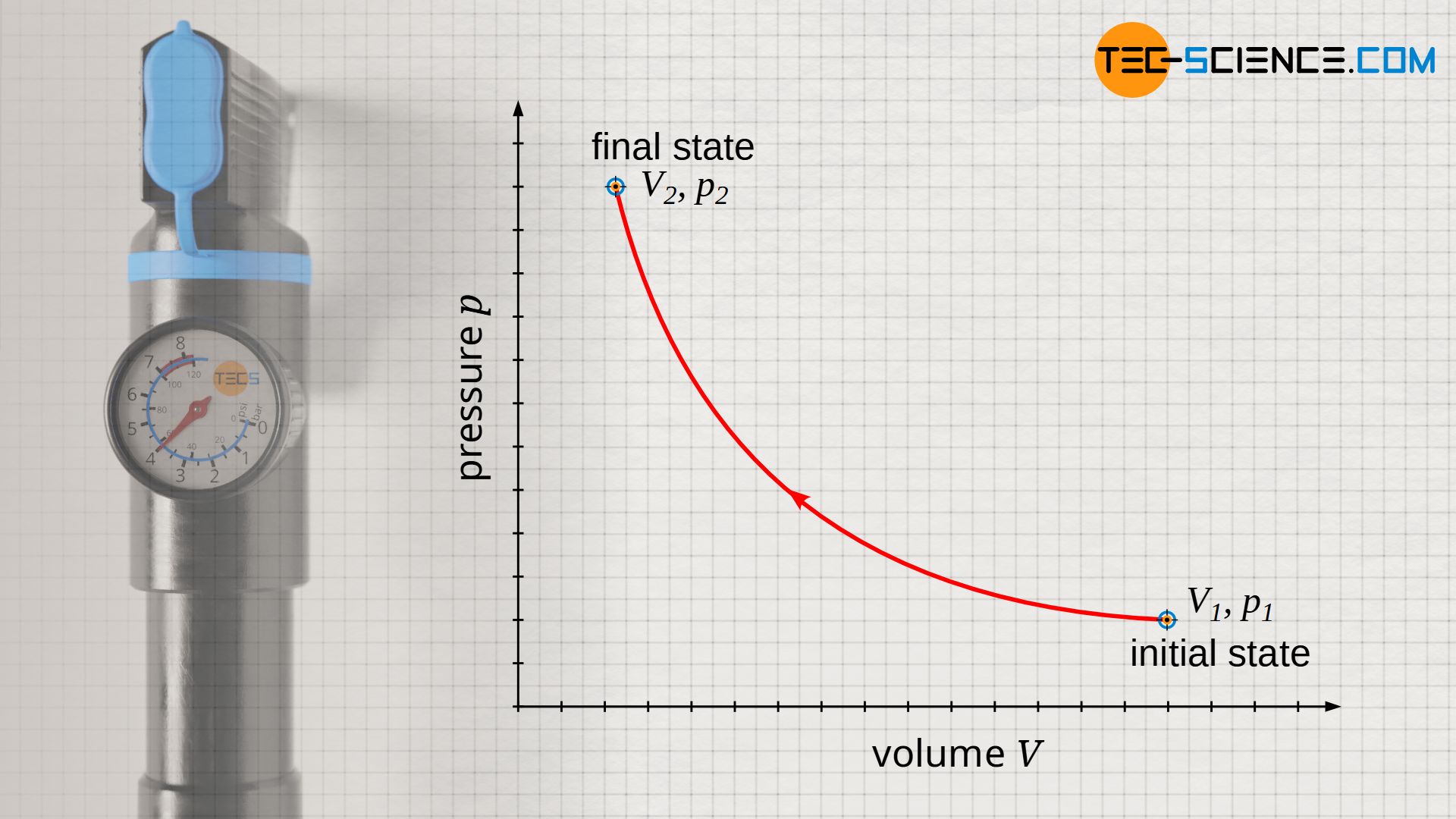
Note that besides the specific gas constant Rs and the mass m (closed system), now also the temperature T is constant. Thus, of course, the product of all three quantities is also constant (Rs⋅m⋅T = constant). Therefore, the isothermal process is represented as a hyperbola in the p(V) diagram.
Relationship between pressure and volume (law of Boyle-Mariotte)
In an isothermal process, the pressure decreases inversely proportionally with increasing volume. A doubling of the volume (expansion) thus means a halving of the gas pressure. Conversely, a halving of the volume (compression) means a doubling of the pressure. This inverse proportionality is equivalent to statement that the product of volume and pressure is always constant in an isothermal process. This phenomenon is also known as law of Boyle-Mariotte:
\begin{align}
p \sim {1 \over V} ~\Rightarrow~ {p \cdot V} = \text{constant}
\end{align}
Any two states within an isothermal process are consequently linked by the constant product of pressure and volume:
\begin{equation}
\label{3}
\boxed{ {p_1 \cdot V_1} = {p_2 \cdot V_2} } ~\text{law of Boyle-Mariotte}
\end{equation}
Calculation of the change in internal energy
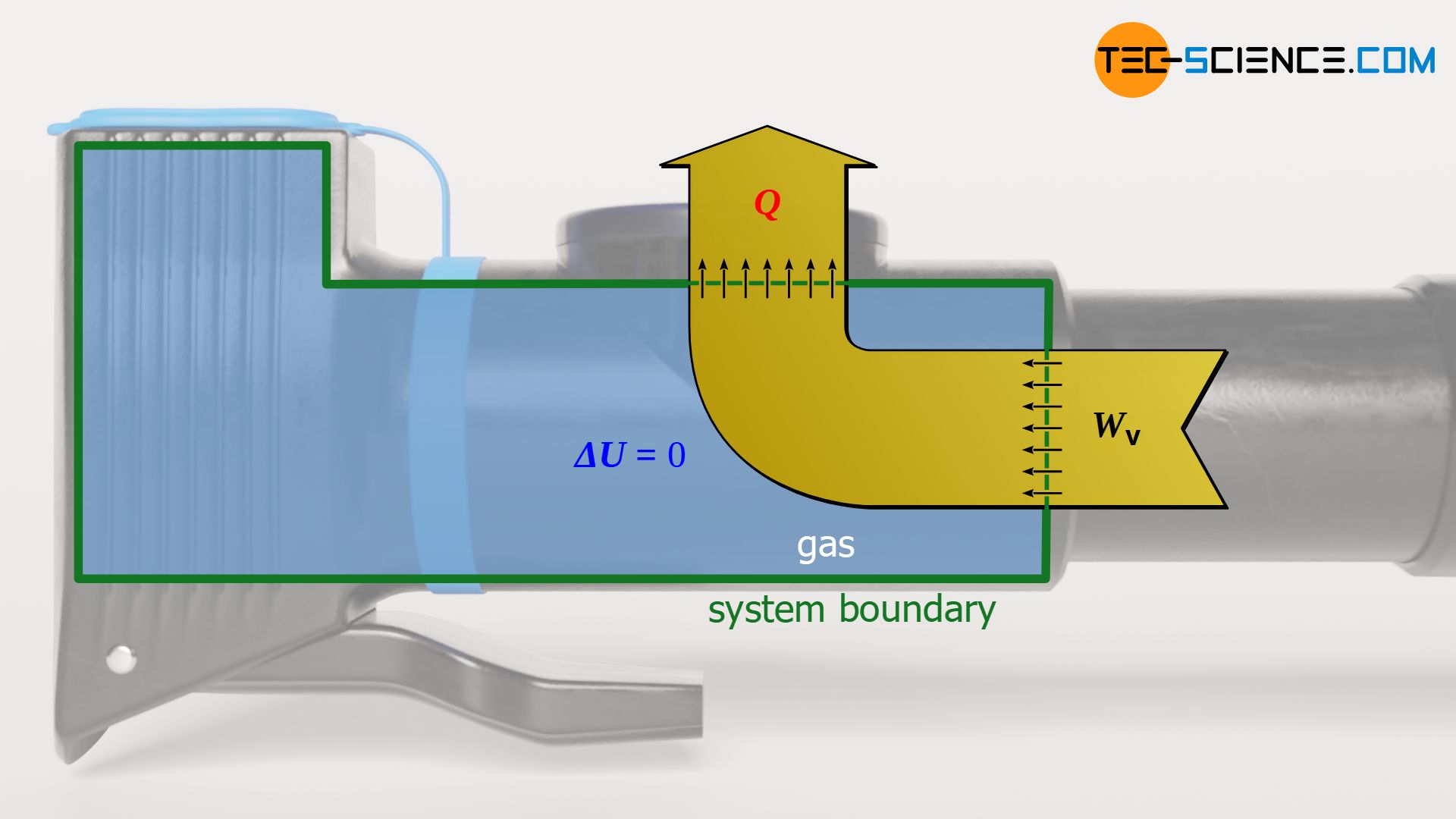
The change of the internal energy ΔU of the gas is directly linked to the temperature change ΔT=T2-T1. However, since the temperature does not change in an isothermal process (T1=T2), the internal energy does not change either. This is also already evident from the physical interpretation of temperature as a measure of the mean kinetic energy of a gas molecule. Because if the temperature does not change, then the speeds of the gas molecules do not change either and the internal energy of the gas remains constant.
\begin{equation}
\boxed{ \Delta U = 0}
\label{eq:1203}
\end{equation}
Calculation of the pressure-volume work
The (pressure-volume) work done by the gas during an isothermal compression can no longer be determined by the product of pressure p and volume change ΔV, as was the case with an isobaric process. This is because as the volume decreases, the pressure increases sharply. This means that as compression progresses, an ever greater force and thus more and more work has to be done on the gas to achieve a further reduction in volume. This can also be seen from the p(V) diagram. In this diagram, the area under the curve corresponds to the pressure-volume work done on the gas to change the volume. The area under the curve increases more and more as the volume becomes smaller.
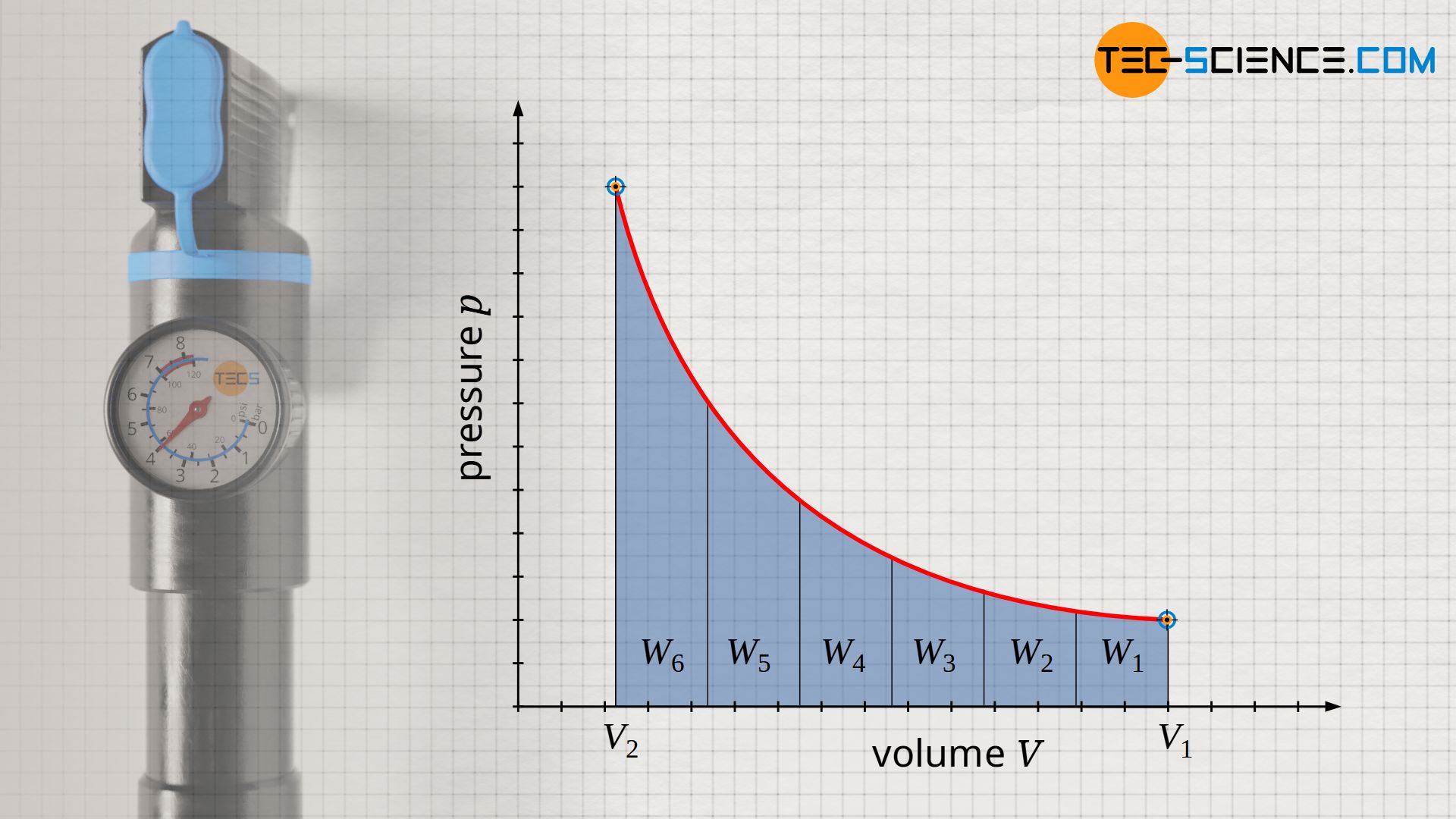
For an isothermal process, the pressure-volume work Wv must be determined as the area under the curve using the integral -∫p(V) dV. For the course of the pressure the function p(V) according to equation (\ref{pv}) has to be used:
\begin{align}
\label{eq:5671}
W_\text{v} &= – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V ~~~~~ \text{ where } ~~~~~ p(V) = R_\text{s}~m~T \cdot {1 \over V} ~~~~~ \text{ : } \\[5px]
&= – \int\limits_{V_1}^{V_2} \underbrace{R_\text{s}~m~T}_{=\text{constant}} \cdot {1 \over V} ~ \text{d}V \\[5px]
&= – R_\text{s}~m~T~ \int\limits_{V_1}^{V_2} {1 \over V} ~ \text{d}V \\[5px] &= – R_\text{s}~m~T~ \left[~\ln(V)~\right]^{V_1}_{V_2} \\[5px]
&= – R_\text{s}~m~T~ \left[ \ln(V_2) – \ln(V_1) \right] \\[5px]
&= R_\text{s}~m~T~ \left[ \ln(V_1) – \ln(V_2) \right] ~\text{ where }~ \underline{\ln(V_1) – \ln(V_2) = \ln \left(V_1 \over V_2 \right)} ~\text{ : } \\[5px]
\end{align}
\begin{equation}
\boxed{W_\text{v} = R_\text{s}~m~T \cdot \ln \left(V_1 \over V_2 \right)} = R_\text{s}~m~T \cdot \ln \left(p_2 \over p_1 \right)
\label{eq:4387}
\end{equation}
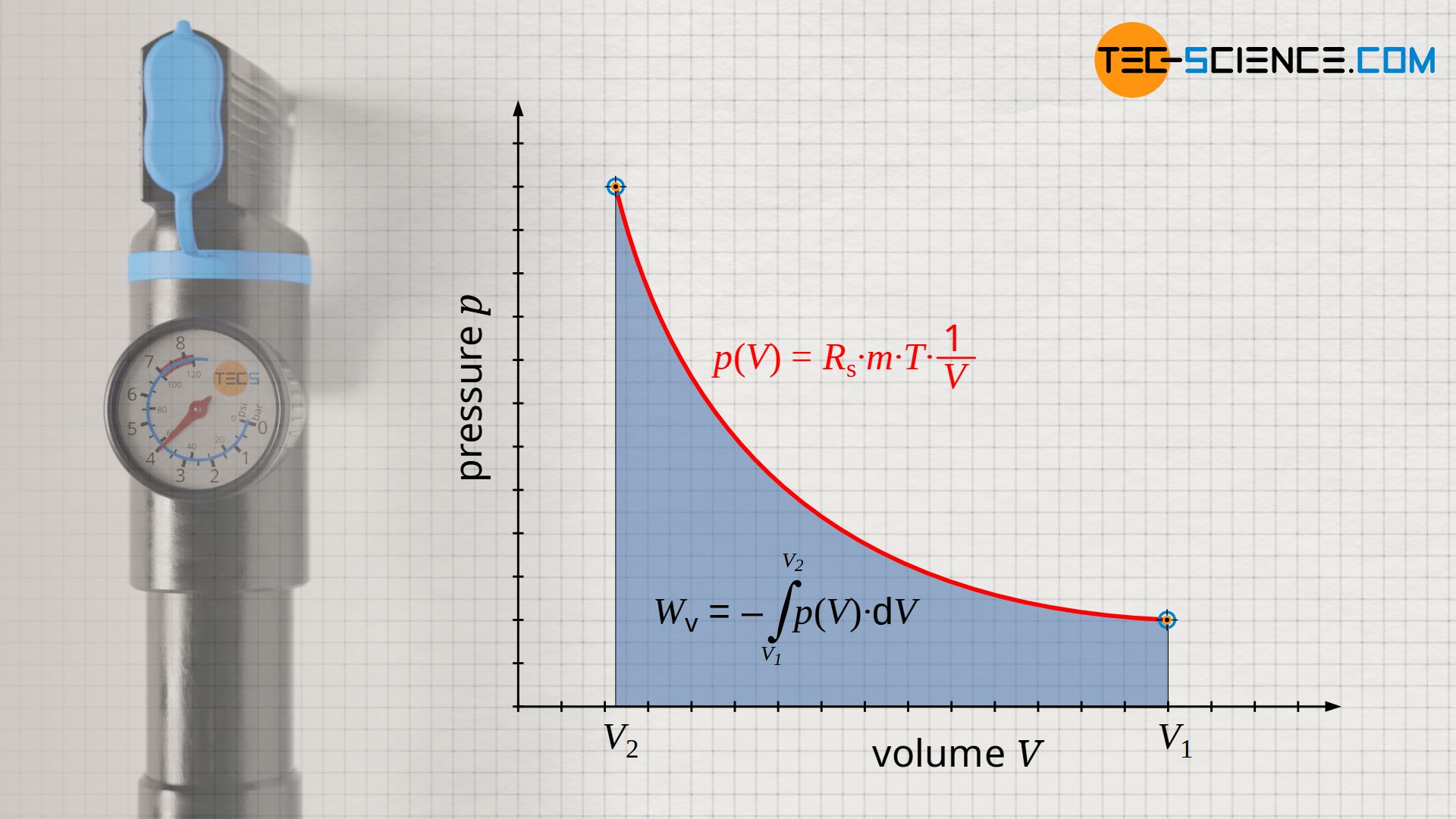
Note that the pressure-volume work can also be calculated by the quotient of final and initial pressure, since according to equation (\ref{3}) the ratio of volumes (V1/V2) is equal to the inverse ratio of pressures (p2/p1=V1/V2).
Calculation of the transferred heat
The pressure-volume work Wv done on the gas or by the gas obviously does not result in a change of the internal energy due to the isothermal process. Of course, this is only possible if the transferred work is compensated to the same extent by releasing or absorbing heat. Work Wv and heat Q are thus equal in amount, but carry opposite signs. This is also evident from the first law of thermodynamics with the condition ΔU=0:
\begin{align}
&W_\text{v} + Q = \overbrace{\Delta U}^{=0} ~~~~~\text{first law of thermodynamics} \\[5px]
&\boxed{Q = – W_\text{v}}
\end{align}