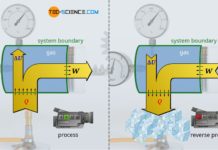
The law of Boyle-Mariotte describes the relationship between a decrease in volume and the resulting increase in pressure at constant temperature (isothermal process).
Isothermal process
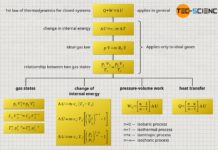
If a thermodynamic process takes place at constant temperature, it is called an isothermal process. For example, the slow compression of air inside an air pump when the outlet valve is closed is such a (quasi-)isothermal change of state.

The compression of the air inside the pump should be done slowly, so that heating can be compensated quickly by the housing and no temperature change occurs. However, if one compresses the air relatively quickly and repeats this often (as is usually the case when using an air pump), then one notices a significant warming of the pump. This must be avoided if the process is to be isothermal.
When compressing the air, one notices an increase in pressure with decreasing volume. The exact mathematical relationship between gas pressure and gas volume for an isothermal process in a closed system is explained in more detail in this article.
Experimental investigation
Experimental setup
A glass cylinder closed with a piston is used to investigate the relationship between volume and pressure. A pressure gauge is connected to the glass cylinder. The gas used is air, which can approximately be regarded as an ideal gas. The gas volume can be varied by the position of the piston. The exact value of the volume can be read off the scale. The pressure resulting from the adjusted volume is read off the barometer (absolut pressure!). In this way the dependence of the pressure on the volume at constant temperature can be investigated.

While moving the piston to set different volumes, make sure that the change of state is slow so that the air inside the cylinder does not heat up. In principle, a slight warming during the change of state cannot be avoided. Therefore, always wait a sufficiently long time after changing the position of the piston before measuring the pressure. In this way, temperature changes can be compensated and the change of state can still be considered isothermal.
Evaluation
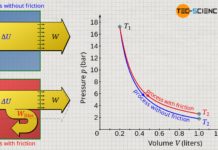
Already during the experiment one notices that the smaller the volume, the greater the pressure. A more precise analysis shows that halving the volume results in a doubling of the pressure. If the volume is only a third of the original value, the pressure has even tripled. If the volume is a quarter, the pressure has already increased fourfold. One also says that volume and pressure are inversely proportional to each other:
\begin{align}
&\boxed{p \sim \frac{1}{V}} ~~~\text{isothermal process of a closed system} \\[5px]
\end{align}
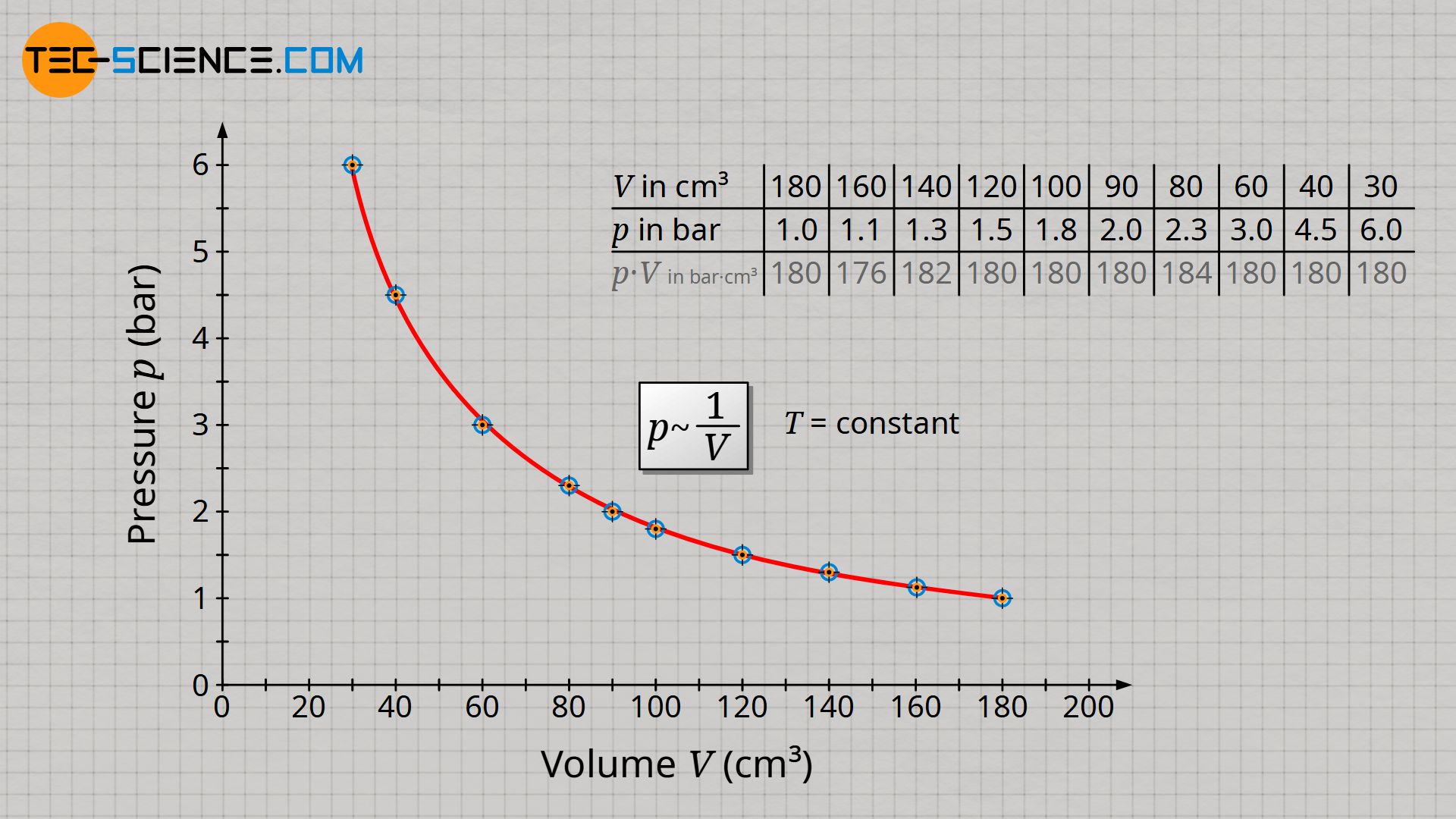
If the series of measurements is illustrated in a volume-pressure diagram, then in this case a so-called hyperbola results as a mathematical relationship between volume and pressure.
Conclusion
If, in the case of an inversely proportional relationship between two quantities, one quantity increases to the same extent as the other quantity decreases, then the product of both quantities is in any case constant. This statement can be verified using the values obtained from the experiment (deviations are caused by uncertainties in the pressure measurement). For an isothermal process, the product of pressure and volume is therefore always constant in any state of the gas:
| Volume V (cm³) | 180 | 160 | 140 | 120 | 100 | 90 | 80 | 60 | 40 | 30 |
| Pressure p (bar) | 1.0 | 1.1 | 1.3 | 1.5 | 1.8 | 2.0 | 2.3 | 3.0 | 4.5 | 6.0 |
| p⋅V (bar⋅cm³) | 180 | 176 | 182 | 180 | 180 | 180 | 184 | 180 | 180 | 180 |
\begin{align}
&\boxed{p \cdot V = \text{constant}}~~~~~\text{law of Boyle-Mariotte} \\[5px]
\end{align}
The constancy of the product of pressure and volume of an isothermal process was experimentally investigated by physicists Robert Boyle and Edme Mariotte. Therefore, this law is also known as Boyle-Mariotte’s law.
Boyle-Mariotte’s law states that for an isothermal process of a closed system, the product of pressure and volume is constant!
Linking two states of a gas
For an isothermal process, the product of pressure and volume therefore has the same constant value in all states of the gas. Therefore it is especially true that the product of pressure and volume in any initial state 1 also corresponds to the product of pressure and volume in any other final state 2:
\begin{align}
&p_1 \cdot V_1 = \text{constant}= p_2 \cdot V_2 \\[5px]
&\boxed{p_1 \cdot V_1 = p_2 \cdot V_2} \\[5px]
\end{align}

For an isothermal process of a closed system, two states of an ideal gas are linked by the product of pressure and volume!
Connection to the ideal gas law
The relationship between two gas states shown above also results from the ideal gas law for the special case of a change of state at constant temperature (T1=T2):
\begin{align}
\require{cancel}
&\frac{p_1 \cdot V_1}{\cancel{T_1}} = \frac{p_2 \cdot V_2}{\cancel{T_2}} \\[5px]
&\boxed{p_1 \cdot V_1 = p_2 \cdot V_2 } \\[5px]
\end{align}
The constancy of the product of pressure and volume can also be derived directly from the ideal gas law. In the case that the temperature does not change (T=constant) and the system is closed (m=constant) the following statement applies:
\begin{align}
&p \cdot V = \underbrace{R_\text{s} \cdot m \cdot T}_{=\text{constant}} ~~~~~\text{ideal gas law}\\[5px]
&\boxed{p \cdot V =\text{constant}} \\[5px]
\end{align}