An isentropic process is a reversible process of an adiabatic system.
Definition
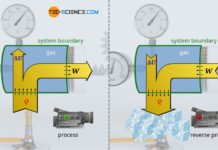
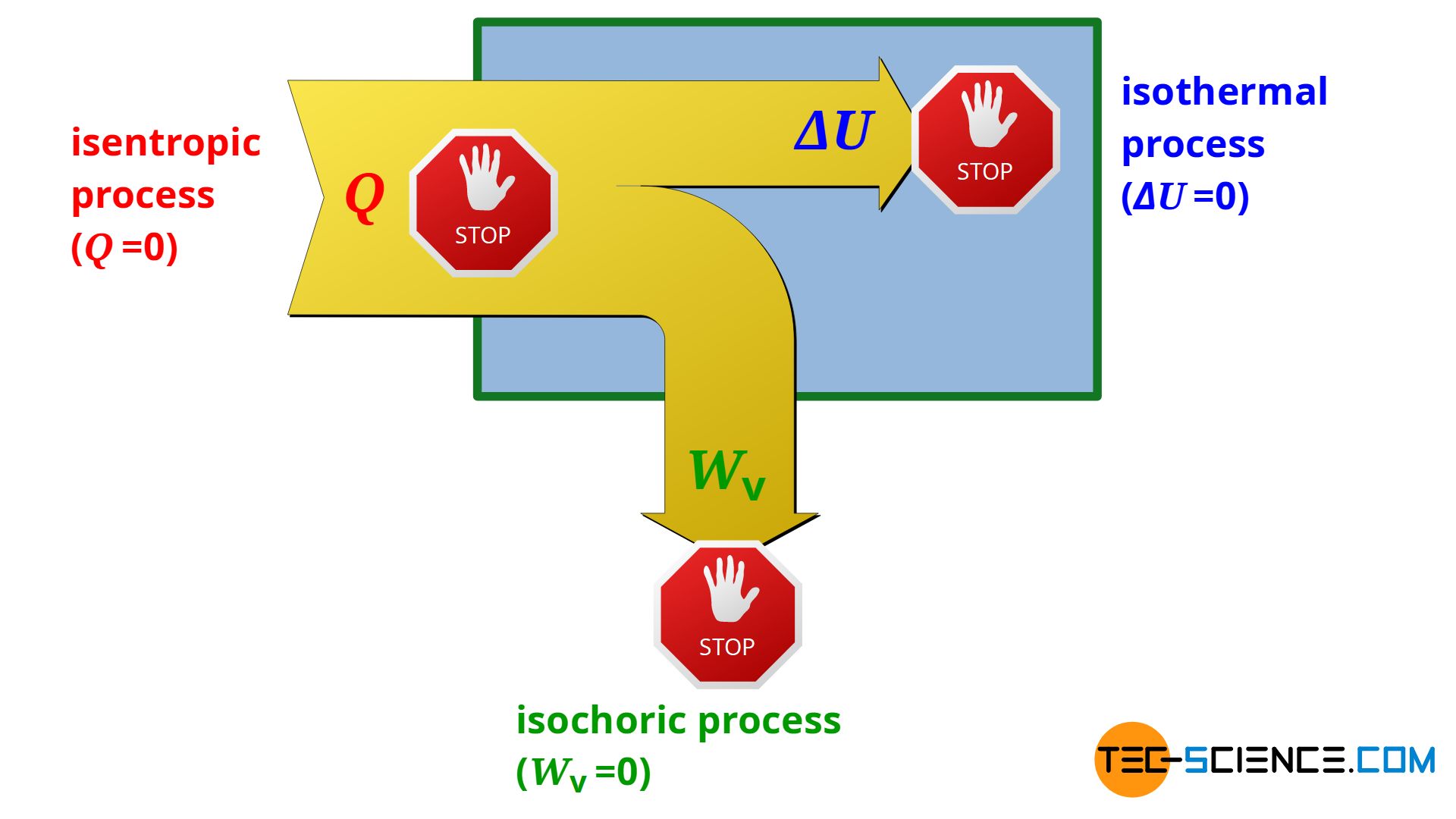
Whereas in an isochoric process no pressure-volume work is done by the system or on the system (Wv=0) and in an isothermal process no change in internal energy takes place (ΔU=0), in a so-called isentropic process, by definition, no heat is transferred across the system boundary (Q=0). Thus, an isentropic process only takes place in an adiabatic system! For this reason, the isentropic process is also referred to as an adiabatic process.
How to achieve an approximately isentropic process
Basically, no system is perfectly thermally insulated, so that an isentropic process can only be approximated. But even if systems are not particularly well thermally insulated, thermodynamic processes can still be regarded as approximately isentropic under certain conditions. This is the case, for example, when thermodynamic processes occur so rapidly that the system has no time to transfer heat across the system boundary. For this reason, the compression and expansion of the fuel-air mixture in internal combustion engines, for example, which take place within a few milliseconds, are often considered isentropic.
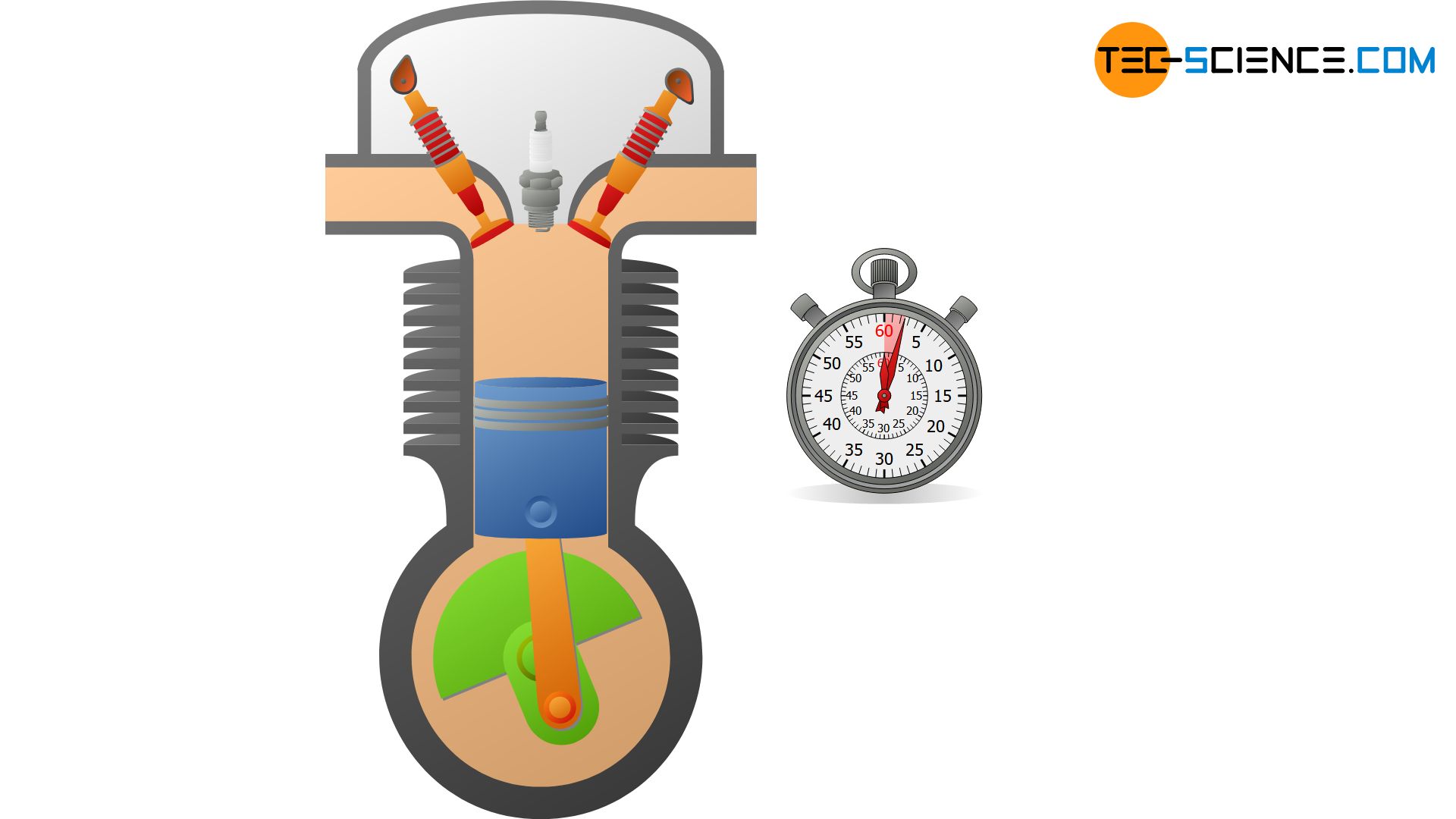
A closed adiabatic system can be realized approximately with a gas-filled cylinder, which is closed with a piston. If the gas is now compressed very quickly, heat transfer to the surroundings can be neglected and an approximate adiabatic system is obtained for the time the compression takes place. Ideally, the walls of the cylinder are still made of a heat-insulating or poorly heat-conducting material.
In practice, the rapid compression of air in an air pump is also approximately an isentropic process when the outlet valve is closed. After compression, however, a drop in pressure is quickly observed, since heat is then transferred from the enclosed air to the inner walls of the air pump. The temperature and thus the pressure drop. The air pump then no longer represents an adiabatic system.

Illustration in the volume-pressure diagram
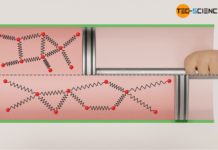
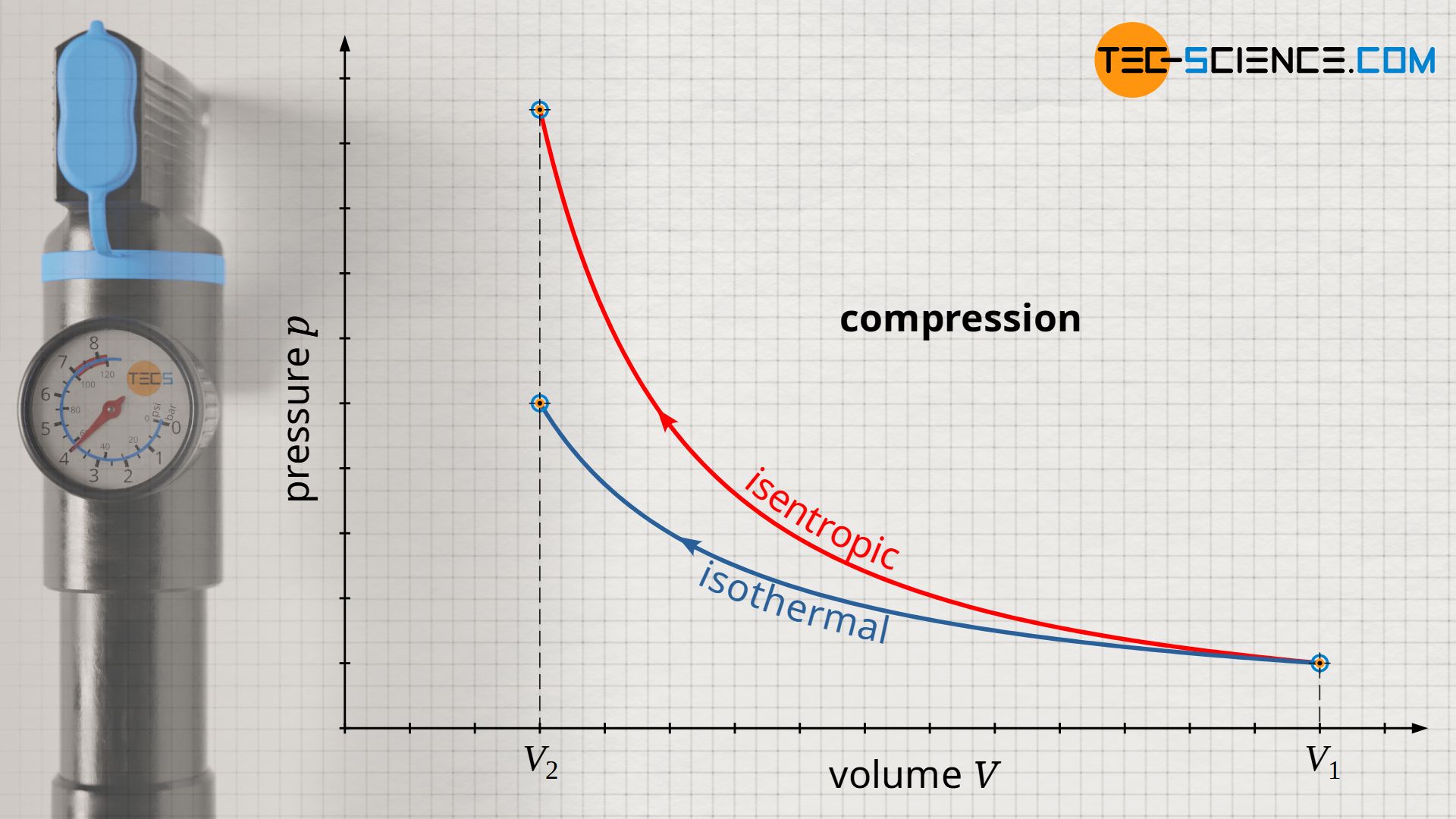
If a gas is compressed abruptly in an adiabatic system, there is an increase in pressure due to the reduction in volume. However, this is also associated with an increase in temperature. This can be explained by the increased momentum (increased speed) of the gas molecules due to the collisions between the rapidly moving piston and the molecules (see also the article Why do pressure and temperature increase during the compression of a gas?) In diesel engines, the temperature increase during compression, which is considered to be isentropic, is deliberately desired, as this causes the ignition temperature of the diesel fuel to be exceeded and the fuel to ignite (self-ignition).
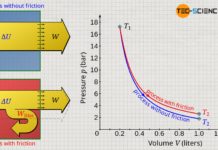
While in the case of isothermal compression a temperature increase is compensated by heat dissipation, in the case of isentropic compression there is, by definition, no heat transfer. Therefore, the increase in pressure is greater for an isentropic process than for an isothermal process. This is because while in isothermal compression the pressure increase results only from the reduction in volume (the temperature remains constant), in isentropic compression there is an temperature increase. This temperature increase further increases the pressure.
Conversely, the pressure drops to a lower value in an isentropic expansion compared to an isothermal expansion. This is because in order to keep the temperature constant during an isothermal expansion, heat must be supplied to the gas. The molecules obviously maintain their kinetic energy due to the constant temperature (constant internal energy). In an isentropic expansion, on the other hand, no heat is transferred to the gas to keep the temperature constant. Therefore, the temperature decreases as the volume increases. Thus, in isentropic expansion, the decrease in pressure results not only from the increase in volume, but also from the decrease in temperature.
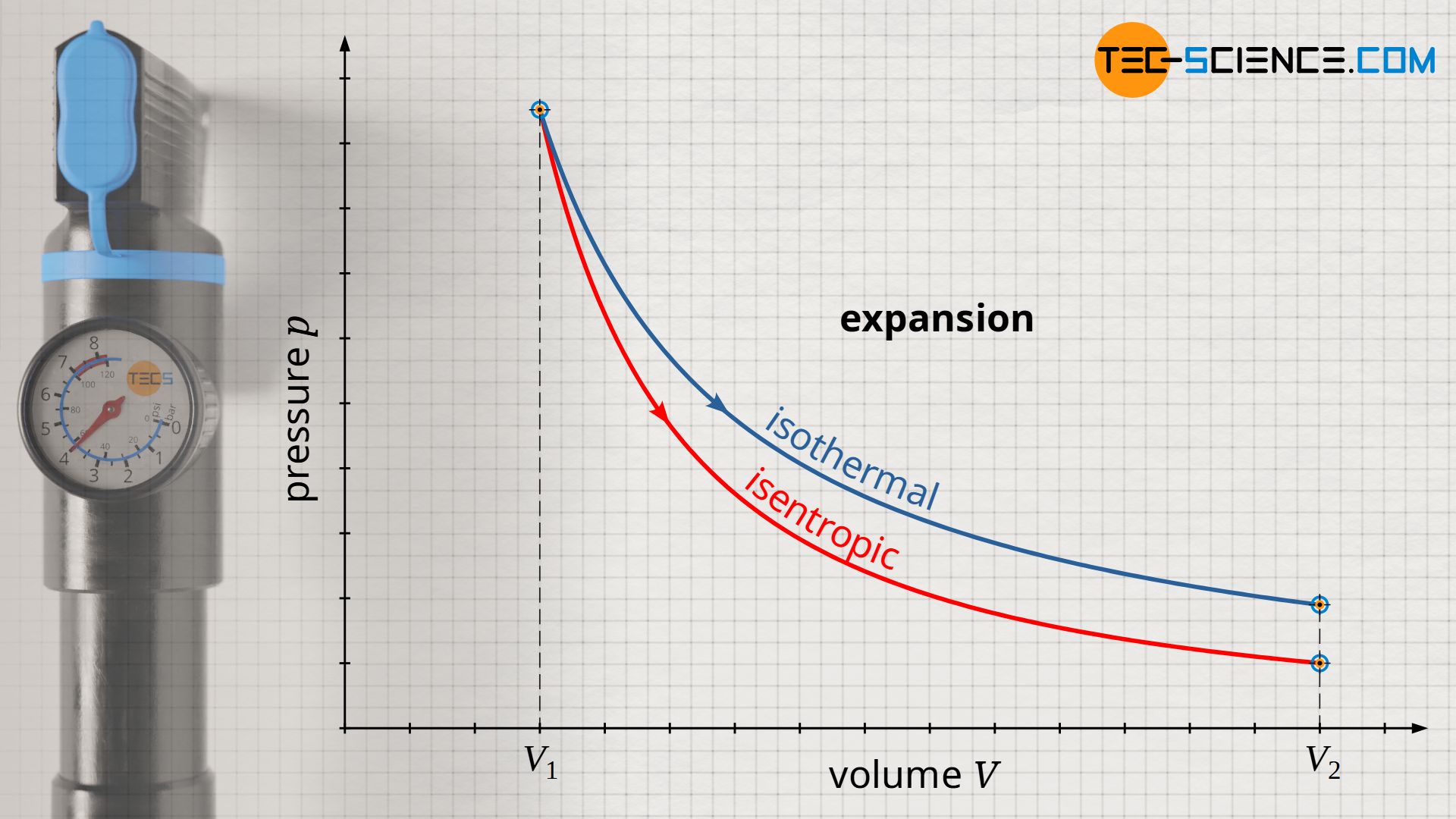
The pressure curve of an isentropic process is steeper in the volume-pressure diagram compared to an isothermal process!
Relationship between volume, pressure and temperature
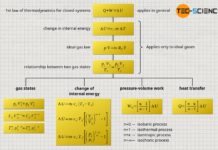
As long as the gas is considered to be an ideal gas, the ideal gas law still applies, regardless of the exact thermodynamic process. Therefore, for an isentropic process in a closed system, two gas states are related by the following equation:
\begin{align}
&\boxed{p \cdot V = R_\text{s} \cdot m \cdot T} ~~~\text{ideal gas law} \\[5px]
&{p \cdot V \over T}=R_\text{s} \cdot m = \text{constant} \\[5px]
\label{kurz}
\Rightarrow~ &\boxed{{p_1~V_1 \over T_1}={p_2~V_2 \over T_2} }\\[5px]
\end{align}
While at this point for an isobaric process the constant pressure, for an isochoric process the constant volume and for an isothermal process the constant temperature can be cancelled from the equation (\ref{kurz}), now for an isentropic process no constant quantities can be found. However, clear relationships between two quantities can be derived if the ideal gas law and the first law of thermodynamics are taken into account with the restriction that now no heat is transferred (see article Derivation of the formulas of the isentropic “adiabatic” process). This results in the following relationships:
\begin{alignat}{3}
\label{2}
&p \cdot V^\kappa = \text{konstant}& &\Rightarrow&~ &\boxed{ p_1~V_1^\kappa = p_2~V_2^\kappa} \\[5px]
\label{3}
&T \cdot V^{\kappa-1} = \text{konstant}& &\Rightarrow&~ &\boxed{ T_1~V_1^{\kappa-1} = T_2~V_2^{\kappa-1}} \\[5px]
\label{4}
&T^\kappa \cdot p^{1-\kappa} = \text{konstant}& &\Rightarrow&~ &\boxed{ T_1^\kappa~p_1^{1-\kappa} = T_2^\kappa~p_2^{1-\kappa}} \\[5px]
\label{1}
&&&&&\text{ mit } \boxed{\kappa = {c_\text{p} \over c_\text{v}}}>1 \\[5px]
\end{alignat}
Since the ratio of the specific heat capacities cp and cv occurs very frequently when deriving these equations, this quotent is conveniently combined to form the so-called heat capacity ratio κ, also known as adiabatic index or Laplace’s coefficient. This ratio is unitless and always greater than 1, since the specific heat capacity cp is always greater than cv (see also the article Specific heat capacity of gases).
If we consider the relationship between pressure and volume according to equation (\ref{2}), it is now also mathematically clear that the pressure curve in the volume-pressure diagram is steeper for an isentropic process than for an isothermal process:
\begin{align}
&p \cdot V^\kappa = \text{konstant} \\[5px]
&\boxed{p \sim {1 \over V^\kappa}} ~~~\text{isentropic process}\\[5px]
&\boxed{p \sim {1 \over V}} ~~~\text{isothermal process}\\[5px]
\end{align}
For an isothermal process, the pressure decreases with increasing volume according to the law p~1/V. For an isentropic process, on the other hand, the pressure decreases according to the law p~1/Vκ. Since the adiabatic index κ is always greater than 1, the pressure obviously decreases more rapidly with an isentropic increase in volume than with the isothermal process.
Calculation of the change in internal energy
For ideal gases, the change in internal energy ΔU results independent of the thermodynamic process only on the basis of the temperature change ΔT=T2-T1:
\begin{align}
\label{a}
&\boxed{ \Delta U = c_\text{v}~m~\left(T_2-T_1 \right)} \\[5px]
\end{align}
If this equation is solved for the temperature ratio T2/T1, the change in internal energy at a given initial temperature T1 can also be determined by the volume ratio or the pressure ratio by linking with equation (\ref{3}) or equation (\ref{4}):
\begin{align}
& \Delta U = c_\text{v}~m~\left(T_2-T_1 \right) \\[5px]
& \Delta U = c_\text{v}~m~T_1~\left[{T_2 \over T_1}-1 \right] \\[5px]
& \boxed{\Delta U = c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{\kappa-1}}-1 \right]} \\[5px]
\label{c}
& \boxed{\Delta U = c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-\kappa} \over \kappa}}-1 \right]} \\[5px]
\end{align}
Calculation of the pressure-volume work
As in any (reversible) thermodynamic process, the pressure-volume work of the gas is given by the area under the curve in the volume-pressure diagram. This area can basically be determined by integrating the pressure function p(V). However, a closer look at the first law of thermodynamics shows that under the constraint Q=0 the pressure-volume work just corresponds to the change of the internal energy:
\begin{align}
&\boxed{W_\text{v} + Q = \Delta U} ~~~\text{First Law of Thermodynamics}\\[5px]
&\boxed{W_\text{v} = \Delta U} \\[5px]
\end{align}
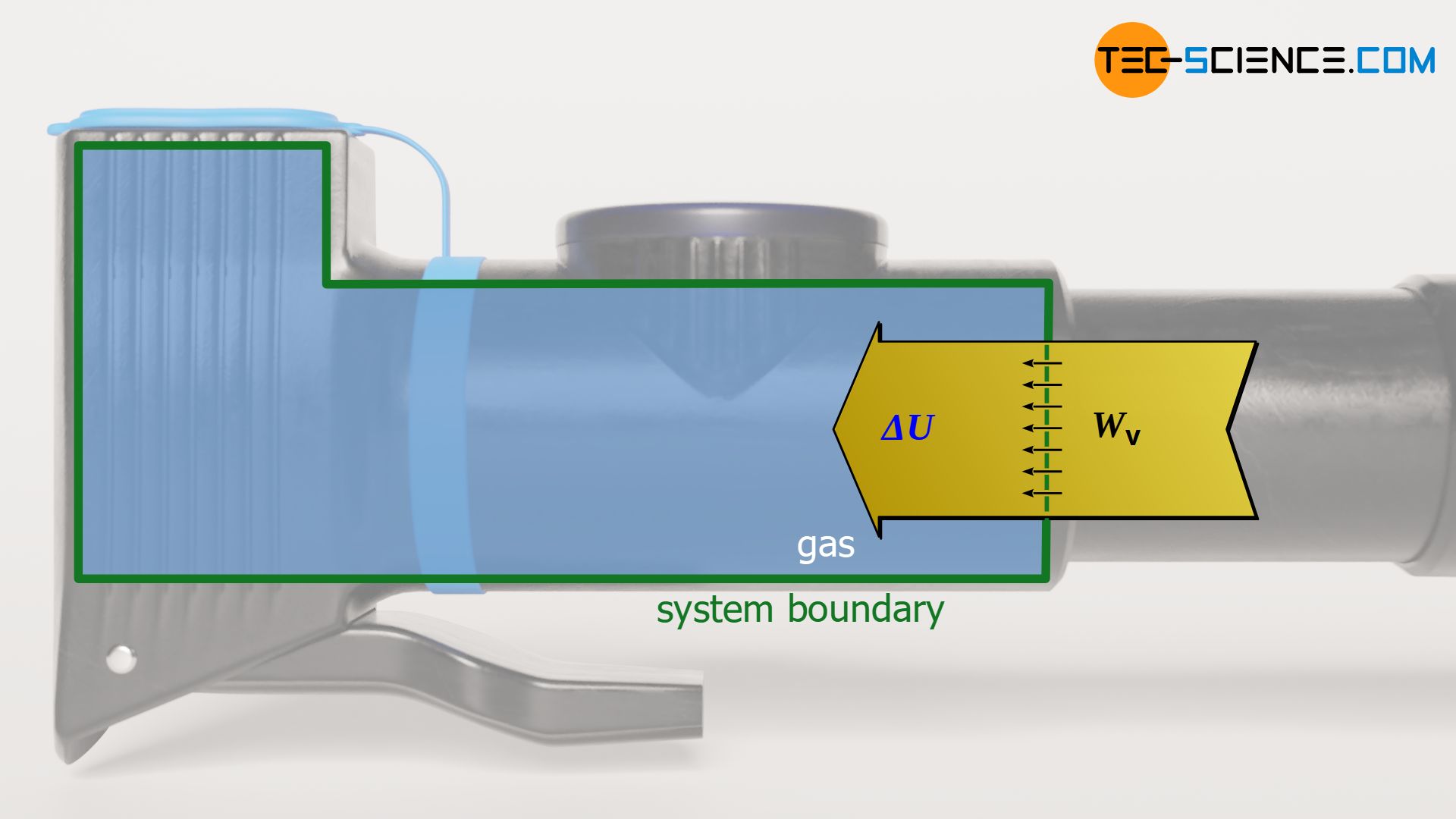
The fact that the change of the internal energy just corresponds to the pressure-volume work also becomes clear very quickly. Due to the lack of transferred heat, the pressure-volume work done on the gas by compression must completely benefit the internal energy. Conversely, a pressure-volume work done by the gas is carried out completely at the expense of the internal energy, since it obviously cannot originate from a heat transfer. To calculate the pressure-volume work Wv during an isentropic process, the equations (\ref{a}) to (\ref{c}) can be used:
\begin{align}
& W_\text{v} = c_\text{v}~m~\left(T_2-T_1 \right) \\[5px]
&W_\text{v} = c_\text{v}~m~T_1~\left[{\left(V_1 \over V_2 \right)^{\kappa-1}}-1 \right] \\[5px]
&W_\text{v} = c_\text{v}~m~T_1~\left[{\left(p_1 \over p_2 \right)^{{1-\kappa} \over \kappa}}-1 \right] \\[5px]
\end{align}
Important note
Attention: Not all thermodynamic processes that take place in an adiabatic system must necessarily obey the equations explained in this article! Therefore, the term adiabatic process is somewhat misleading. The strict definition of the isentropic process is as follows:
An isentropic process is a reversible change of state of an adiabatic system!
At this point the term reversible is crucial! More information, especially about this topic, can also be found in the article Free expansion of an ideal gas in a vacuum.