Learn more about calculating the internal energy for ideal gases in this article.
First law of thermodynamics
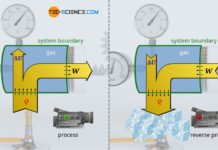
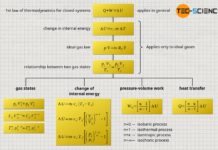
In the article Internal energy of ideal gases it was explained in detail that in ideal gases only the kinetic energy of the gas molecules exists as internal energy (thermal energy). According to the first law of thermodynamics, this internal energy can be changed by transferring energy as work W or as heat Q:
\begin{align}
&\boxed{\Delta U = W + Q } ~~~~~\text{change in internal energy} \\[5px]
\end{align}

According to the Maxwell-Boltzmann distribution, the kinetic energy of the molecules is in turn directly related to the gas temperature. Thus, a change of the internal energy (change of the kinetic energy) inevitably means a change of temperature. This raises the question how a change in internal energy ΔU is related to a change in temperature ΔT.
Preliminary considerations for determining the change in internal energy
As already mentioned, the kinetic theory of gases shows a direct relationship between the mean kinetic energy of the molecules in a gas and its temperature. So if you know the temperature of a gas (and the number of particles), then a certain internal energy is directly connected with it. This is independent of the pressure or volume of the gas. Therefore the change of the internal energy is only dependent on the change of the temperature.
The change of internal energy during a thermodynamic process is thus clearly determined in ideal gases, if the initial temperature (and thus the initial energy) and the final temperature (and thus the final energy) are known. Whether it is an isobaric, isochoric, isentropic or any other process is therefore irrelevant for the change of the internal energy. Only the change of temperature determines the change of the internal energy!
The fact that the internal energy is only dependent on the state of the gas (in terms of temperature) and not on the type of process, makes the internal energy a state variable. In contrast to this, heat and work depend on the thermodynamic process (whether isochoric, isothermal, isobaric or isentropic) and therefore are considered process quantities.
So, if one wants to investigate the relationship between a change of internal energy and a temperature change, this can be done in principle with any thermodynamic process. The results obtained from this process is then also valid for any other thermodynamic process, i.e. in general for ideal gases. At this point, the isochoric process is particularly suitable for investigating the relationship, since no work is done on the gas or by the gas with such a process. A heat input therefore increases the internal energy by the same amount and is therefore relatively easy to investigate. This will be discussed in more detail in the next section.
Derivation of the relationship using the example of an isochoric process
To determine the relationship between a change in internal energy and the change in temperature the following experiment is performed. A gas of mass m is confined to a vessel of constant volume. By transferring heat, the temperature of the gas increases and with it the internal energy.

Since the volume of the gas cannot change during such an isochoric process, energy cannot be transferred as work by expansion or compression (W=0). According to the first law of thermodynamics, the heat Q transferred to the gas thus completely increases the internal energy ΔU:
\begin{align}
& \Delta U = \underbrace{W}_{=0}+Q= Q \\[5px]
\label{u}
& \underline{\Delta U = Q} \\[5px]
\end{align}

Thus, in order to determine the relationship between a change in internal energy and the change in temperature, it is not necessary to carry out elaborate investigations of the kinetic energy of the individual molecules. According to equation (\ref{u}) only the relationship between a heat input Q of an isochoric process (which then directly corresponds to the change in internal energy ΔU) and the resulting temperature increase ΔT has to be investigated. By using an electric heater, the supplied energy can be determined relatively easily (“heat = electrical power x time”).
The experiment shows that the temperature change ΔT is proportional to the transferred heat Q, i.e. a temperature change twice as large requires twice as much heat:
\begin{align}
\label{q}
& Q \sim \Delta T \\[5px]
\end{align}
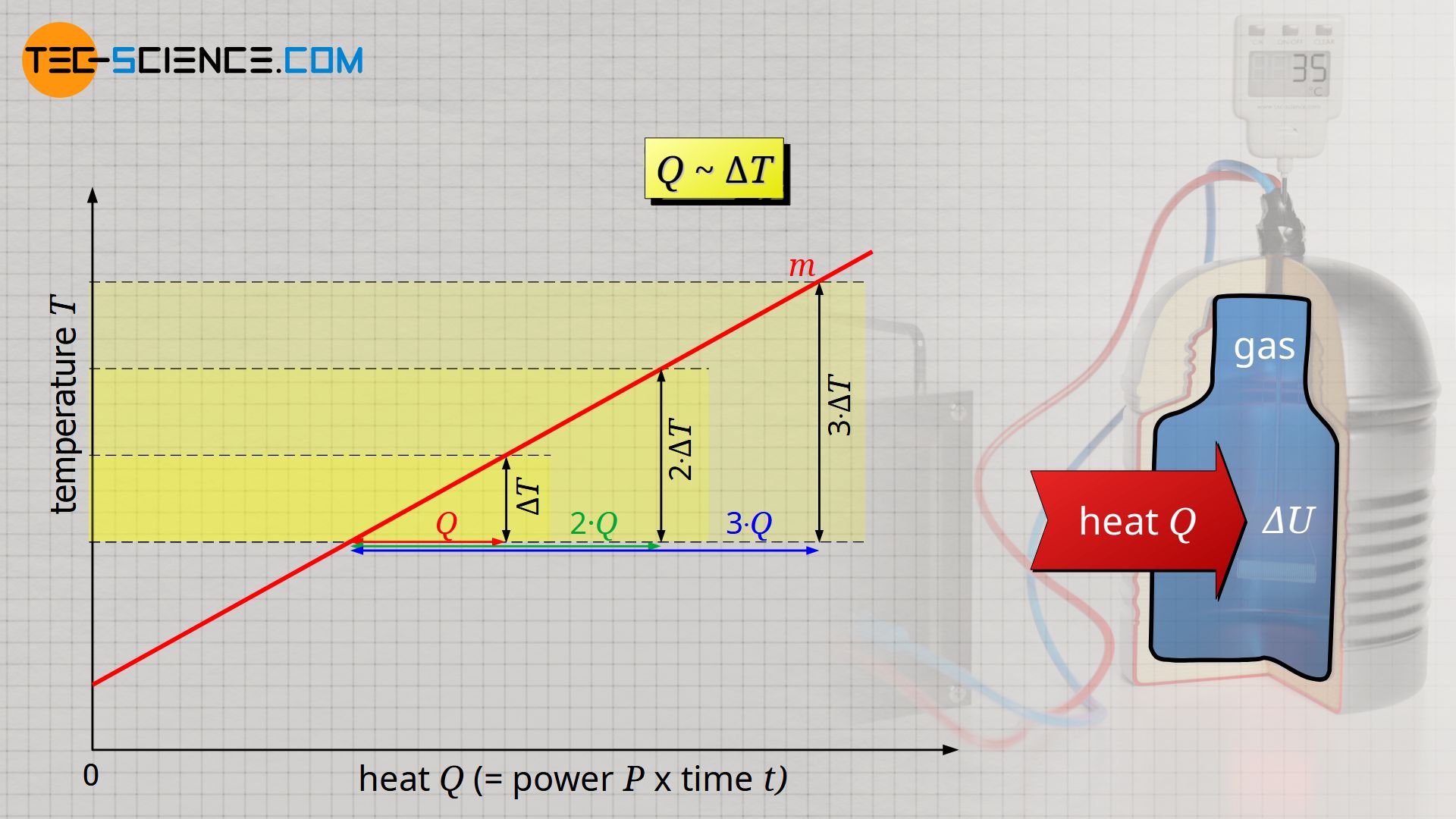
It is also observed that the more heat is required, the greater the mass of gas to be heated. For a mass twice as large, twice as much heat Q is required to heat the gas. Heat Q and mass m are therefore also proportional to each other:
\begin{align}
\label{m}
& Q \sim m \\[5px]
\end{align}
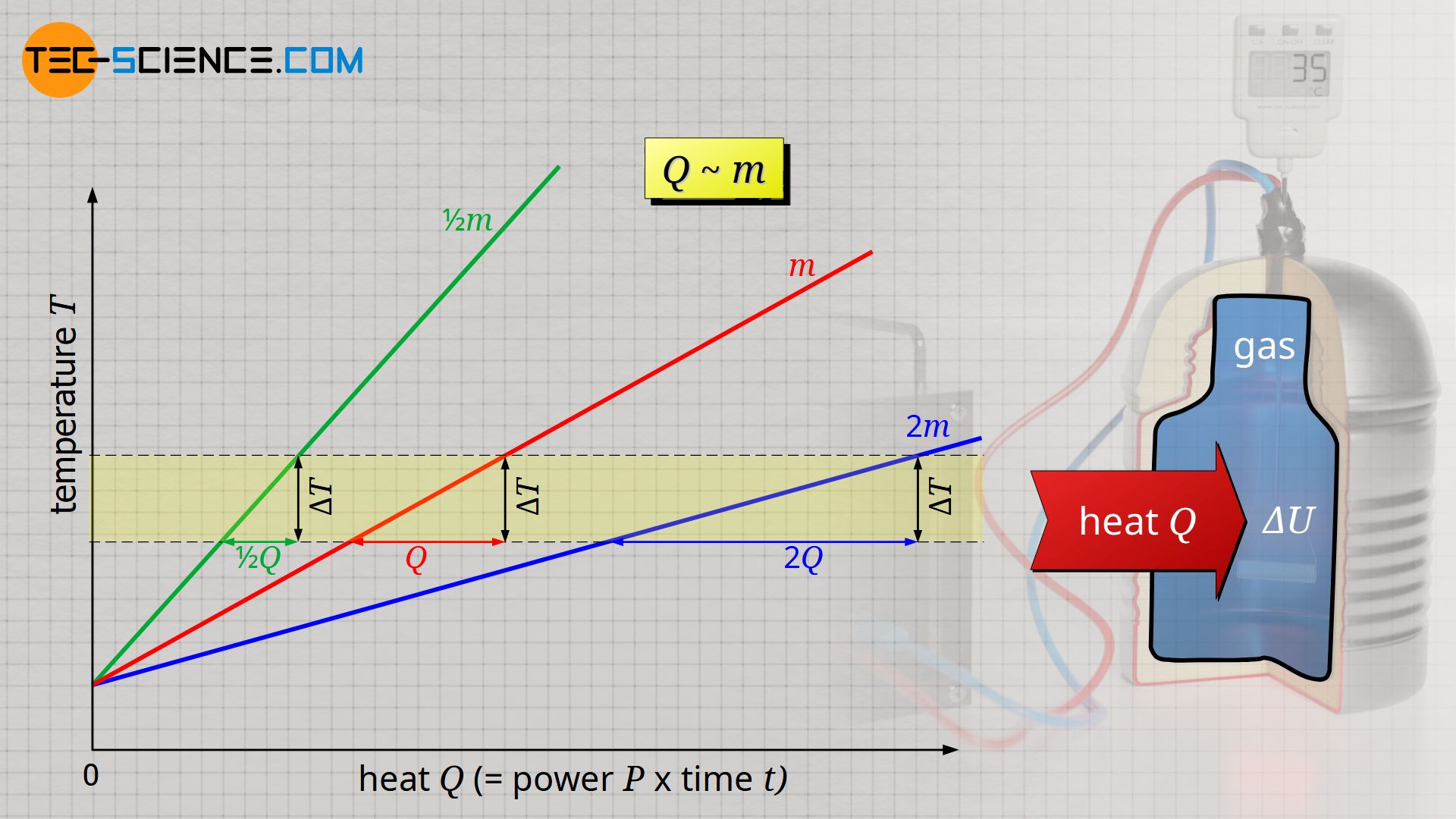
All in all, the transferred heat Q is proportional to the mass m and the temperature change ΔT of the gas. The proportionality constant between these quantities is called the specific isochoric heat capacity cv and is only dependent on the type of gas:
\begin{align}\;\;\;\;\;
& Q \sim m \cdot \Delta T \\[5px]
\label{c}
& \underline {Q = c_\text{v} \cdot m \cdot \Delta T} ~~~~~ [c_\text{v}]=\frac{\text{J}}{\text{kg} \cdot \text{K}} ~~~\text{specific isochoric heat capacity} \\[5px]
\end{align}
The specific heat capacity indicates how much energy is required to change the temperature of a substance of mass 1 kg by 1 K. Or in this case: by how much the internal energy changes per unit mass when the temperature changes by 1 K. According to the equation (\ref{u}), the sought-after relationship between the change in internal energy ΔU and the temperature change ΔT for an ideal gas has now been found:
\begin{align}\;\;\;\;\;
\label{d}
& \boxed{ \Delta U = c_\text{v} \cdot m \cdot \Delta T} ~~~\text{where } \Delta T = T_2-T_1~~~\text{applies in general to ideal gases!} \\[5px]
\end{align}
Remark on the formula
At this point, one should not be misled by the term “specific isochoric heat capacity” cv, which appears in formula (\ref{d}). In context with the change of internal energy, the quantity cv should only be considered as a proportionality constant between the change of internal energy and the change of temperature.
This proportionality constant is called specific isochoric heat capacity only because for the isochoric process (and only for the isochoric process!) this quantity describes the transferred heat – see equation (\ref{c}). But when it comes to the change of internal energy, equation (\ref{d}) applies to any thermodynamic process of ideal gases – see section “Preliminary considerations for determining the change in internal energy”!
Internal energy of ideal gases
Even though in thermodynamics often only the change of internal energy ΔU is relevant, for ideal gases the absolute internal energy U can also be determined. To do this, imagine a gas confined to a cylinder with constant volume that is cooled down to absolute zero. In this state, all molecules are at rest and the gas therefore has no internal energy. Now heat Q is transferred at constant volume to the gas until it reaches a temperature T. All the heat that was necessary to heat the gas is finally present as internal energy U. Thus, at a temperature T the gas has the following internal energy U:
\begin{align}
\label{t}
& \boxed{ U = c_v \cdot m \cdot T} ~~~\text{applies in general to perfect gases!} \\[5px]
\end{align}
Note: Strictly speaking, the specific isochoric heat capacity cv for ideal gases may also be temperature dependent. Namely, when degrees of freedom are frozen with decreasing temperature due to quantum mechanical effects. Equations (\ref{d}) and (\ref{t}) are then no longer valid without restrictions. However, if one assumes that such a temperature dependence does not exist, one often speaks of perfect gases and equations (\ref{d}) and (\ref{t}) still apply without restriction.
Analogy between internal energy and gravitational potential energy
Internal energy of ideal gases can very clearly be compared in analogy to gravitational potential energy of an object. While the gravitational potential energy represents the energetic (gravitational) state of an object at a given height h, the internal energy represents the energetic (kinetic) state of an ideal gas at a given temperature T.
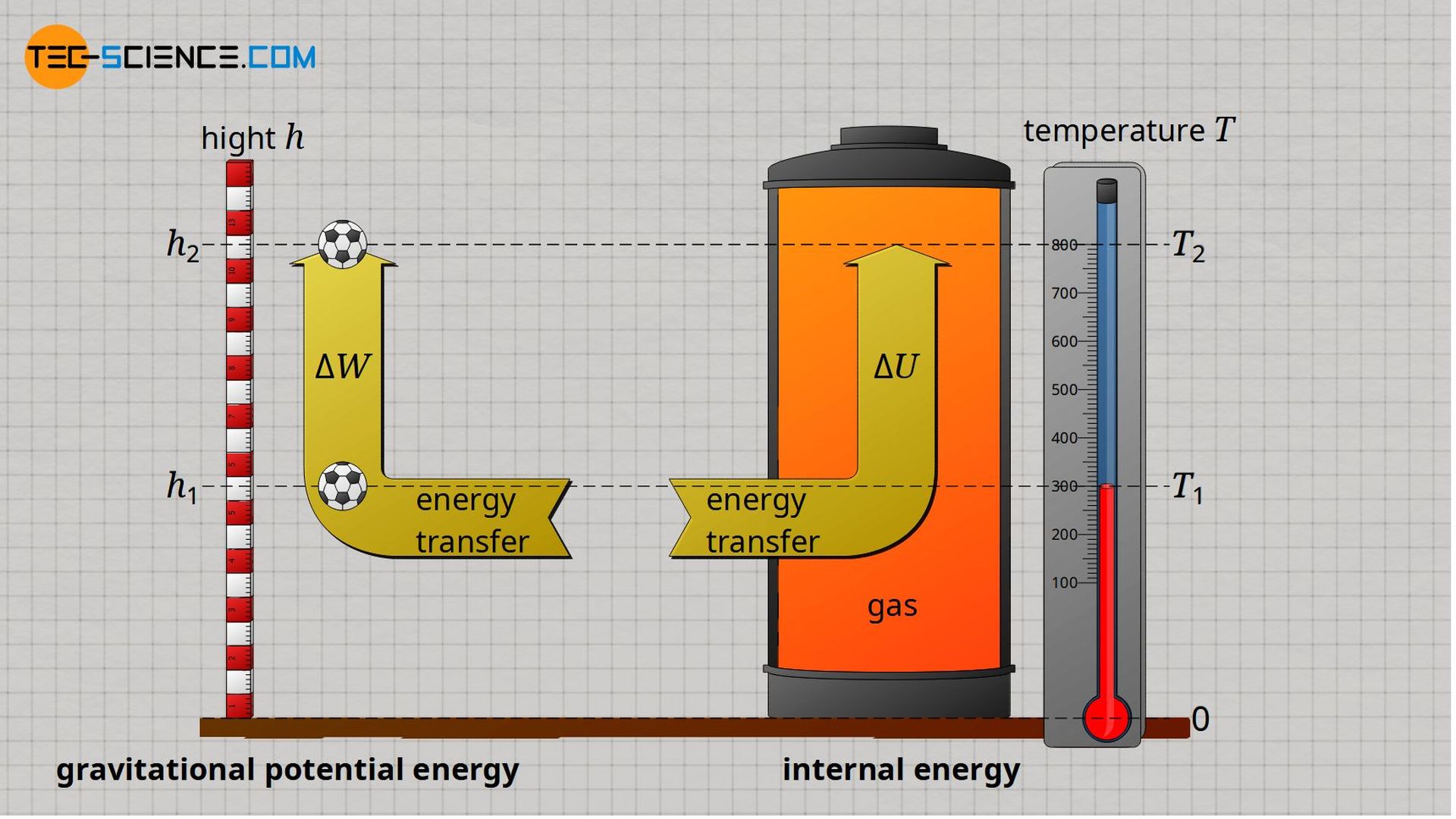
A given height h can be assigned a certain potential energy via the mass m of the object. In the same way, a certain internal energy can be assigned to a given temperature T via the mass m of the gas. The exact relationship between the potential energy and the height h is established by the gravitational acceleration g (dependent on the position!). In the case of internal energy, the relationship between internal energy U and temperature T is established by the specific isochoric heat capacity cv (dependent on the type of gas!).
| Gravitational potential energy | Internal energy |
|---|---|
| height h | temperature T |
| mass of the object m | mass of the gas m |
| gravitational acceleration g | specific isochoric heat capacity cv |
| gravitational potential energy W = m⋅g⋅h | internal energy U = m⋅cv⋅T |
| change of potential energy ΔW = m⋅g⋅Δh | change of internal energy ΔU = m⋅cv⋅ΔT |
The energetic state of the object located at a height h can be changed by transferring energy – it can be brought to a higher height. In the same way, the energetic state of a gas at a temperature T can be changed by transferring energy – it can be brought to a higher temperature.
The energy required to lift an object from a height h1 to a height h2 depends only on the difference in height Δh = h2 – h1 and is independent of the path! In the same way, the energy required to increase the temperature of an ideal gas from T1 to T2 depends only on the temperature difference ΔT = T2 – T1 and not on the thermodynamic process.