Erfahre in diesem Artikel mehr über die spezifische Wärmekapazität von Stoffen und die Auswirkungen auf das zeitliche Temperaturverhalten bei Wärmezufuhr oder Wärmeabfuhr.
Definition der spezifischen Wärmekapazität
Die spezifische Wärmekapazität gibt anschaulich an, wie viel Wärmeenergie nötig ist, um 1 Kilogramm eines Stoffes um 1 K (1 °C) zu erwärmen. Je größer die spezifische Wärmekapazität c eines Stoffes also ist, desto mehr Wärme Q ist nötig, um eine bestimmte Temperaturänderung ΔT hervorzurufen (gleiche Masse m vorausgesetzt):
\begin{align}
\label{q}
& \boxed{Q = c \cdot m \cdot \Delta T} ~~~~[c] = \frac{\text{kJ}}{\text{kg}\cdot \text{K}} \\[5px]
\end{align}

Die spezifische Wärmekapazität gibt nicht nur für eine Erwärmung den Zusammenhang zwischen Wärmezufuhr und Temperaturerhöhung wieder; auch für eine Abkühlung gilt diese Stoffgröße gleichermaßen. In diesem Fall stellt die spezifische Wärmekapazität den Zusammenhang zwischen einer Wärmeabfuhr und der resultierenden Temperaturerniedrigung her.
Zeitlicher Verlauf der Temperatur bei Erwärmung
Stoffe mit großen Wärmekapazitäten ändern ihre Temperatur bei Wärmezufuhr oder Wärmeabfuhr also nicht so stark wie Stoffe mit geringen Wärmekapazitäten. Dies wird nach Umstellen von Gleichung (\ref{q}) nach der Temperaturänderung auch direkt ersichtlich:
\begin{align}
& \boxed{\Delta T = \frac{Q}{c \cdot m}} \\[5px]
\end{align}
Führt man einem Stoff nicht einmalig Wärme zu, sondern kontinuierlich, dann wird sich auch die Temperatur permanent erhöhen (sofern keine Aggregatzustandsänderung eintritt). Wie schnell die Temperatur dabei ansteigt, hängt von der spezifischen Wärmekapazität ab. Bei Stoffen mit geringen Wärmekapazitäten steigt die Temperatur relativ schnell an, da relativ wenig Wärme benötigt wird, um eine bestimmte Temperaturänderung zu erzielen. Im Gegensatz hierzu nimmt bei Stoffen mit großen Wärmekapazitäten die Temperatur nur relativ langsam zu, da insgesamt mehr Wärme benötigt wird, bis eine bestimmte Temperaturänderung erreicht ist.
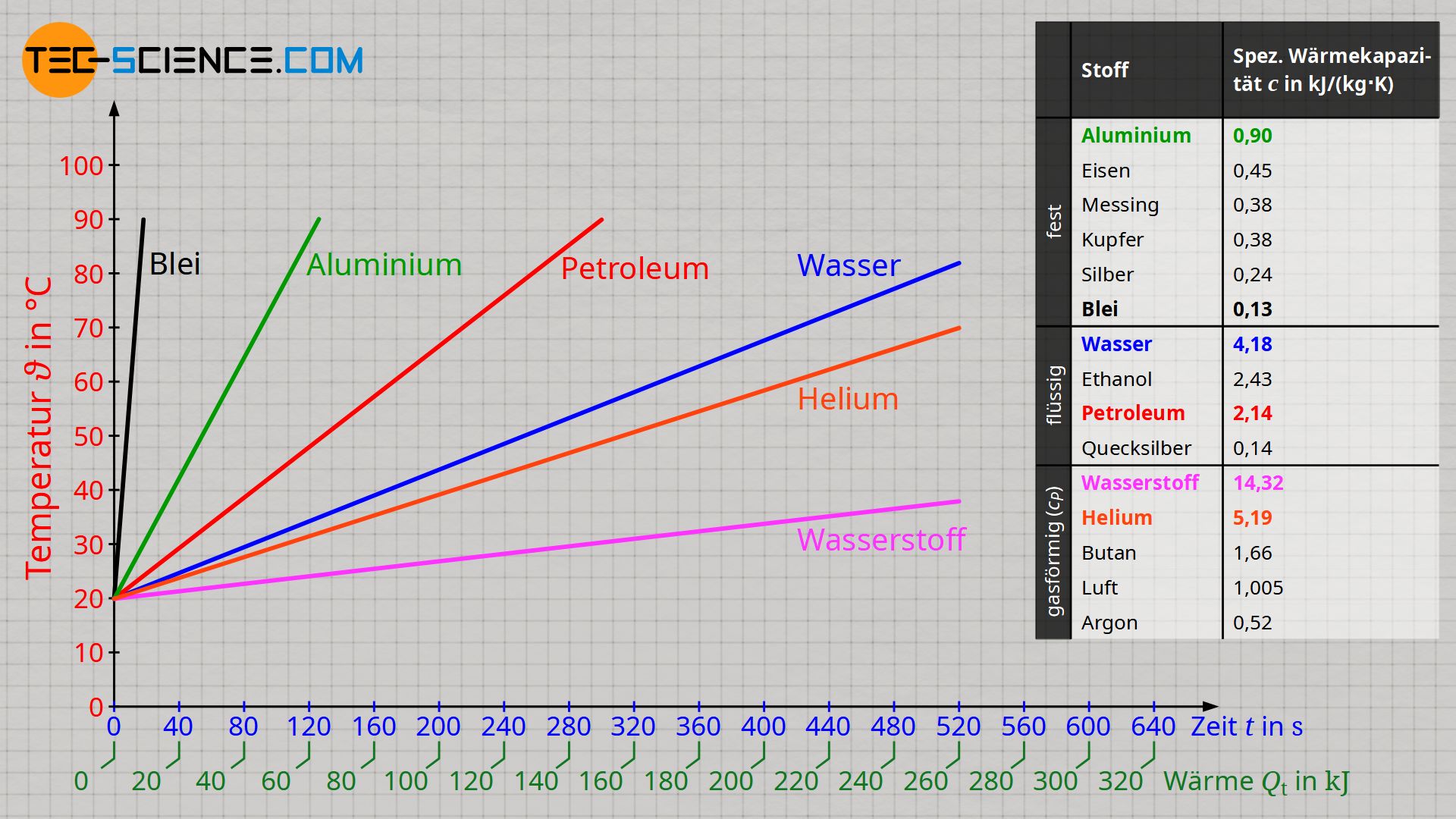
Die obere Abbildung zeigt bei einer Wärmezufuhr von 500 Joule pro Sekunde (= Heizleistung 500 W) die Zeit-Temperatur-Kurven ausgewählter Stoffe mit jeweils einer Masse von 1 Kilogramm. Sofern von einer temperaturunabhängigen spezifischen Wärmekapazität ausgegangen werden kann, handelt es sich bei den Temperaturverläufen um Geraden.
Je höher die spezifische Wärmekapazität eines Stoffes, desto flacher verläuft die Erwärmungskurve bei konstanter Heizleistung (gleiche Massen vorausgesetzt)!
Spezifische Wärmekapazität ausgewählter Stoffe
In der Tabelle unten sind die spezifischen Wärmekapazitäten ausgewählter Stoffe aufgeführt.
| Stoff | Spezifische Wärmekapazität c in kJ/(kg⋅K) bei 20 °C |
|---|---|
| Feststoffe | |
| Aluminium | 0,90 |
| Eisen | 0,45 |
| Messing | 0,38 |
| Kupfer | 0,38 |
| Silber | 0,24 |
| Blei | 0,13 |
| Flüssigkeiten | |
| Wasser | 4,18 |
| Ethanol | 2,43 |
| Petroleum | 2,14 |
| Quecksilber | 0,14 |
| Gase cp (cv) | |
| Wasserstoff | 14,3 (10,1) |
| Helium | 5,19 (3,11) |
| Butan | 1,66 (1,52) |
| Luft | 1,01 (0,72) |
| Argon | 0,52 (0,31) |
Bei Betrachtung der oberen Tabelle, fällt vor allem die große spezifische Wärmekapazität von Wasserstoff von 14,3 kJ/(kg⋅K) auf. Aufgrund dieses hohen Wertes wird Wasserstoff auch zur Kühlung eingesetzt, da es seine Temperatur trotz Wärmezufuhr nur in geringem Maße ändert – es bleibt also sehr lange kalt! Auch Helium besitzt eine solche Eigenschaft. In diesem Zusammenhang wird ein Stoff, der zur Kühlung eingesetzt wird, auch ganz allgemein als Kryogen bezeichnet.
Als Kryogen bezeichnet man Stoffe, die zur Kühlung eingesetzt werden und die vorzugsweise sehr hohe spezifische Wärmekapazitäten aufweisen!
Zwar haben die gasförmigen Stoffe Helium und Wasserstoff eine höhere spezifische Wärmekapazität im Vergleich zu Wasser, dabei darf allerdings nicht vergessen werden, dass diese unter Normalbedingungen und bei gleicher Masse jedoch ein wesentlich größeres Volumen einnehmen! Die untere Abbildung zeigt maßstabsgetreu die entsprechenden Volumina der verschiedenen Stoffe unter Normalbedingungen, d.h. bei einem Druck von 1 bar und einer Temperatur von 0°C.
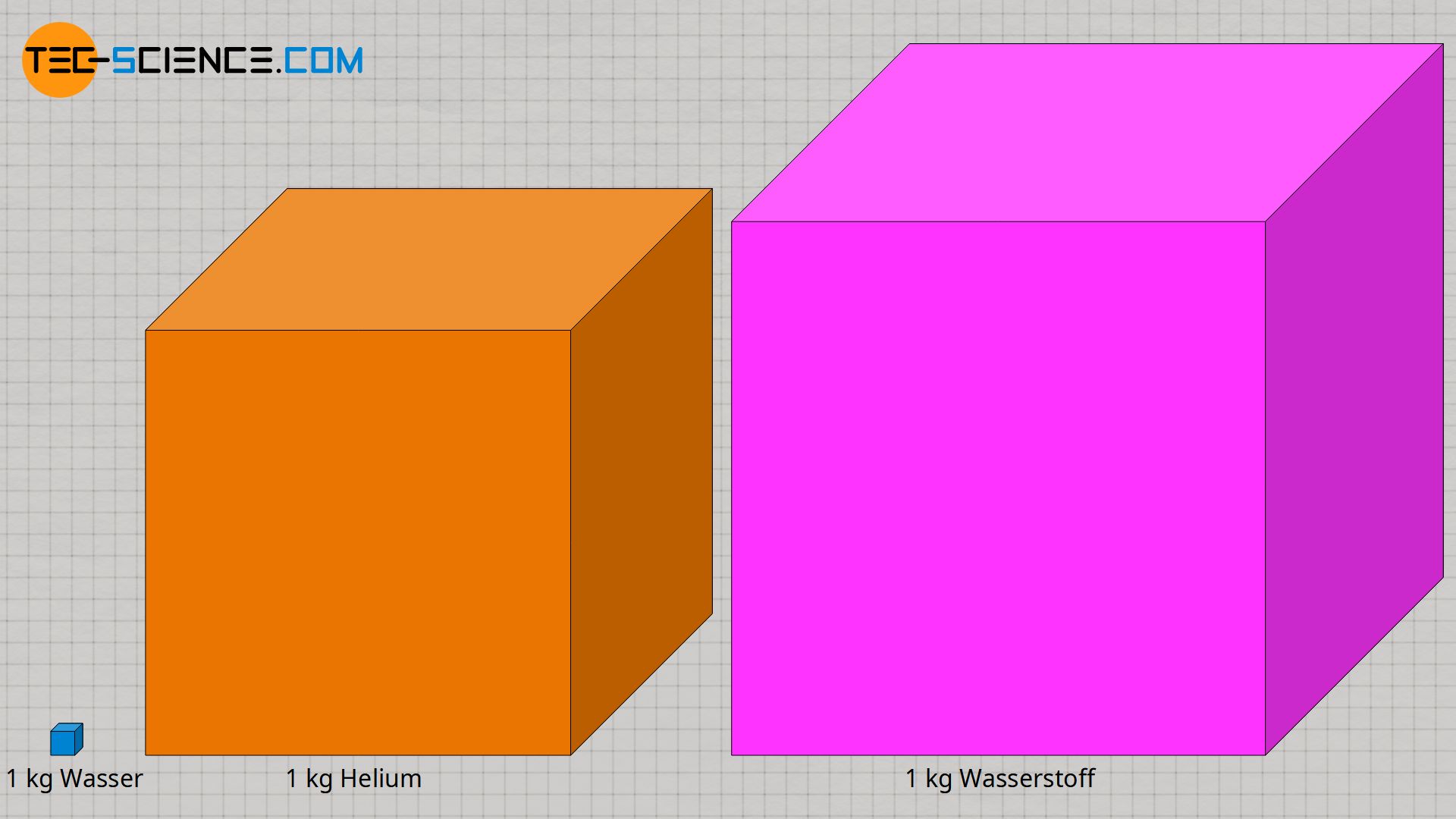
Wasser hat nach Helium und Wasserstoff die größte spezifische Wärmekapazität aller gängigen Stoffe und eignet sich aufgrund der hohen Verfügbarkeit, Handhabbarkeit und aufgrund des geringen Volumens in besonderem Maße für Kühl- oder Heizzwecke im Alltag und in der Technik! Mehr Informationen, speziell zur spezifischen Wärmekapazität von Wasser, finden sich im verlinkten Artikel.
Zu Nutze macht man sich die hohe spezifische Wärmekapazität des Wassers bspw. in Zentralheizungen. So senkt sich die Temperatur des im Heizkörpersystem befindlichen Wassers trotz Wärmeabgabe an die Umgebung nur in geringem Maße – die Heizwirkung hält relativ lange an und erwärmt die umgebende Luft. Die Luft erwärmt sich aufgrund ihrer relativ geringen spezifischen Wärmekapazität von 1 kJ/(kg⋅K) wesentlich stärker. Die Temperatur der Luft nimmt also stärker zu als die Temperatur des Wassers dabei abnimmt (gleiche Masse vorausgesetzt)!
Auch beim Baden in der Badewanne zeigt sich der große Vorteil der hohen spezifischen Wärmekapazität des Wassers, da es somit für relativ lange Zeit warm bleibt. Ebenfalls wird die besondere Eigenschaft des Wassers mit seiner hohen spezifischen Wärmekapazität für Wasserkühlungen genutzt – das kalte Wasser erwärmt sich trotz Wärmezufuhr nicht so stark und behält somit für relativ lange Zeit seine Kühlwirkung.
Spezifische Wärmekapazität von Gasen
Im Gegensatz zu den inkompressiblen Stoffen wie Festkörper und Flüssigkeiten, muss bei kompressiblen Stoffen wie Gasen unterschieden werden, ob Wärme bei konstantem Druck (isobarer Prozess, Index „p“) oder konstantem Volumen (isochorer Prozess, Index „v“) zugeführt wird. Bei einem isobaren Prozess muss grundsätzlich mehr Wärme zugeführt werden, um eine bestimmte Temperaturänderung zur erzielen. Grund hierfür ist, dass die zugeführte Wärmeenergie nicht vollständig für die Temperaturerhöhung genutzt wird, sondern ein Teil für die Verrichtung von Arbeit aufgrund der Volumenausdehnung des Gases aufgebracht werden muss.
Aus diesem Grund ist die spezifische Wärmekapazität bei einem isobaren Wärmeumsatz (cv-Wert) stets größer als bei einem isochoren Wärmeumsatz (cv-Wert). Die Werte für die spezifischen Wärmekapazitäten der isochoren Prozesse sind in der oberen Tabelle in Klammer angegeben. Beachte, dass die Unterscheidung zwischen einer isobaren oder isochoren Wärmezufuhr in der Praxis meist nur für kompressible Stoffe wie Gase vorgenommen werden muss. Mehr Informationen hierzu finden sich im Artikel Spezifische Wärmekapazität von Gasen (bei konstantem Druck bzw. Volumen).