The rate of heat flow refers to the heat energy transferred per unit of time (heat output). The drive for the heat flow is a temperature difference.
Direction of the heat flow
If two objects with different temperatures are in contact with each other, they are tempted to equalize their temperatures over time. The driving force behind this is the striving for thermodynamic equilibrium. Put simply, this means an even distribution of the kinetic energies of the molecules contained in the objects. Since the kinetic energy is ultimately a measure of temperature, this even distribution ultimately corresponds to the establishing of a common mixing temperature. Such an equalization of the kinetic energies (temperatures) can be explained by collisions of the molecules. For more detailed information on this see article Heat and thermodynamic equilibrium.
From the thermodynamic understanding of the concept of heat, it is clear that heat can only ever be transferred from a hotter object (“higher energy”) to a cooler object (“lower energy”). This is because the faster molecules of the hotter substance give off part of their energy to the slower molecules of the cooler substance and not the other way round. That is why in everyday life one will never see a cool body reducing its temperature while warming up a warmer body. Rather, the warmer of the two bodies will always cool down and the colder will warm up.

Heat always flows from points of higher temperature to points of lower temperature!
In simple terms, the heat flow is always directed from warm to cold. For example, the statement “in winter you should close the windows, otherwise cold comes in” should correctly be “in winter you should close the windows, otherwise heat will be released to the outside“!
Definition of the heat flow rate
The heat energy Q transferred per time Δt is called rate of heat flow Q*. The heat flow rate is also referred to as heat output (“energy per unit of time”) and is therefore expressed in the unit Watt (W):
\begin{align}
& \boxed{\dot Q = \frac{Q}{\Delta t}} ~~~[Q]=\frac{\text{J}}{\text{s}}=\text{W} \\[5px]
\end{align}
For a heat flow to occur, a temperature difference must be present. Practice shows that the greater the temperature difference, the greater the rate of heat flow. The temperature difference can thus be regarded as a measure of the driving force of the heat flow (see also the article Thermal conductivity).
The temperature difference is a measure for the driving force of the heat flow!
Heat flow & particle model
The fact that the greater the temperature difference, the greater the heat flow between two objects can be clearly understood with the particle model of matter. This is because the greater the temperature difference between two substances, the greater the difference in the kinetic energies of the respective molecules. Thus, a great amount of energy can be transferred from the “faster” to the “slower” molecules, which ultimately means a great deal of heat transfer. Just imagine a fast bowling ball crashing into a very slow one instead of a relatively slow bowling ball colliding with a slightly slower one. In the first case significantly more energy (“heat”) is transferred.
This also explains why the equalization of the temperatures of two bodies in contact is faster at the beginning than at the end. The temperature difference between the bodies is relatively high at the beginning. This results in a large rate of heat flow. This initially causes a large amount of energy to be transferred from the hotter object to the cooler object per unit time. The temperature of the cooler body rises correspondingly fast and that of the hotter body drops rapidly.
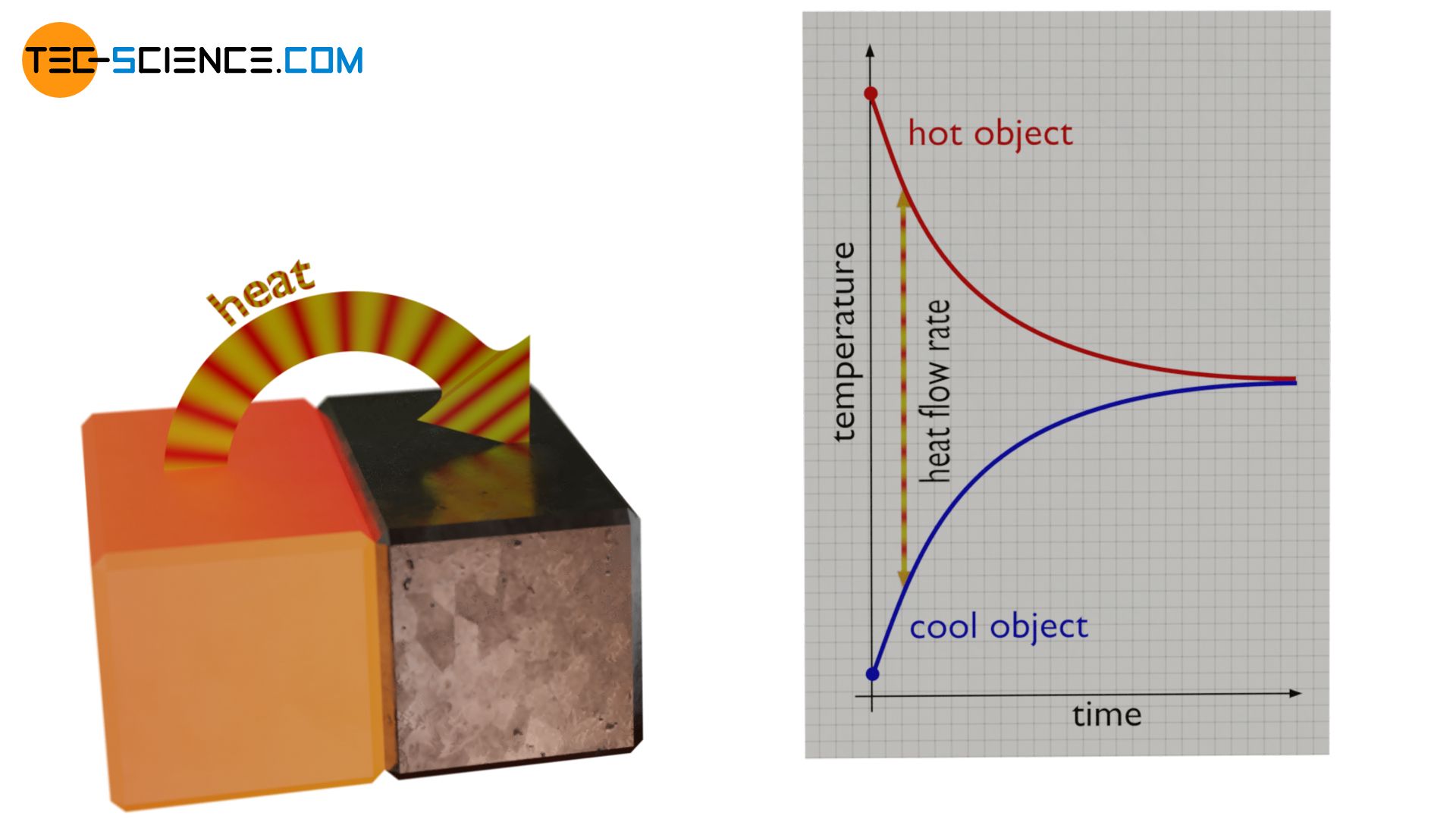
In the further course of time the temperatures become more and more similar. This reduces the temperature difference and the associated rate of heat flow. As a result, less and less energy is transferred per unit time. Therefore, the temperatures do no longer rise or fall as quickly. The process of temperature equalization therefore slows down more and more as time goes by. As soon as the temperatures have equalized, the driving force for the heat flow also comes to a standstill. No more energy is effectively being transferred. The heat transfer is thus completed and thermodynamic equilibrium is reached.
Cooling of a hotplate
The diagram below shows in fast motion the cooling process of a hotplate in air as recorded by a thermal imaging camera. It becomes clear that the temperature drops rapidly immediately after the stove is switched off. However, this cooling process then slows down more and more. Finally, after the initial significant drop in temperature, a lot of time will pass before you can touch the hotplate again.
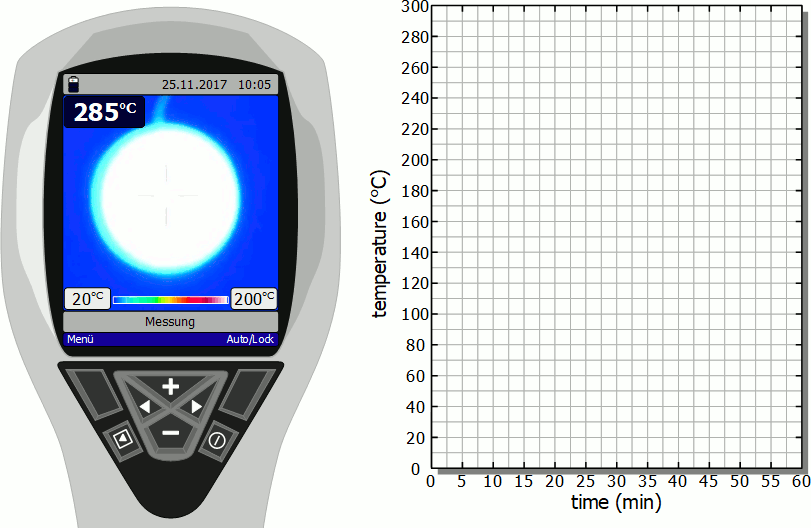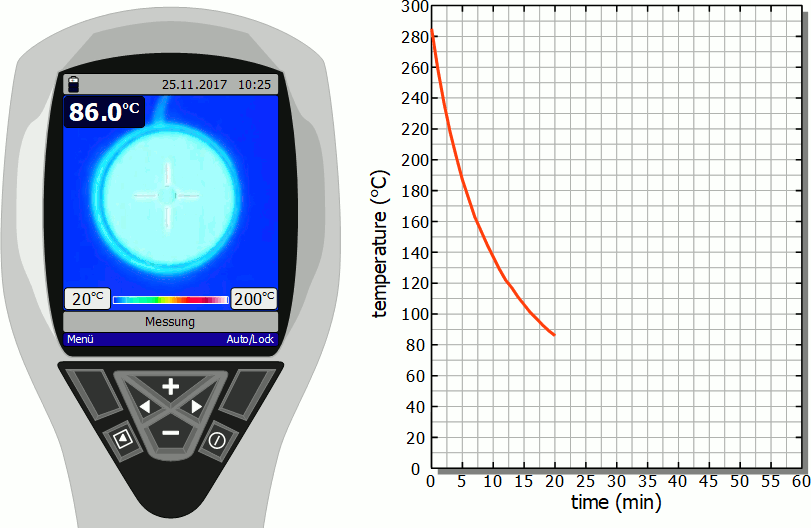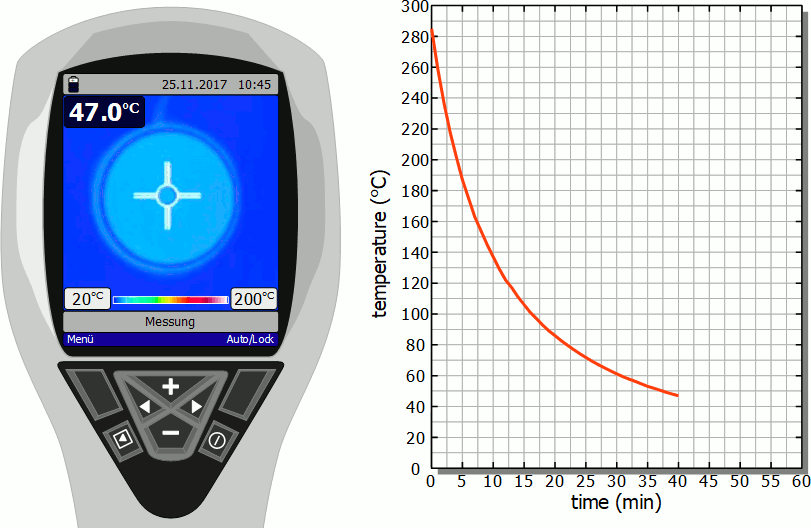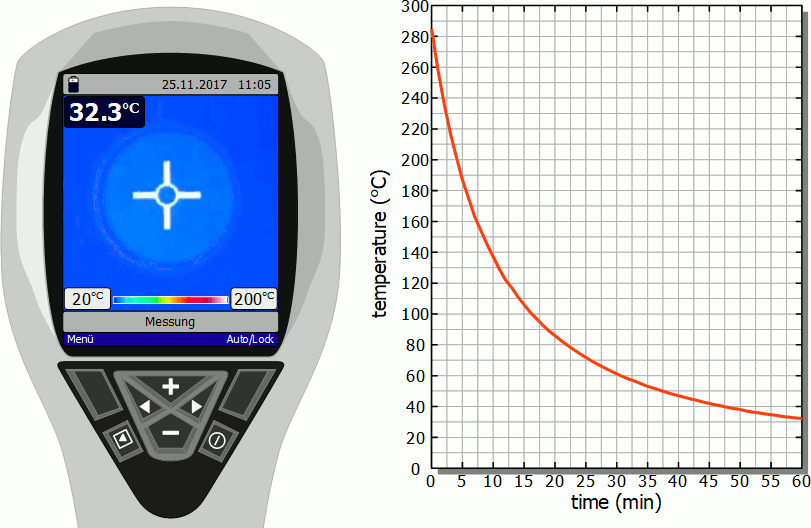
As already mentioned, the slower cooling is due to the decreasing rate of heat flow. As the temperature decreases, the temperature difference to the surroundings also decreases and with it the heat flow rate. The cooling thus gradually slows down.
Note that this process is also an equalization of temperatures. While the temperature of the hotplate drops, theoretically the air temperature of the surroundings rises. However, the latter is usually not observable, as the air temperature increases only minimally due to the large environment. You should therefore not try to heat your home with a hotplate or an oven! This only leads to overheating of the electrical circuits and possibly fatal fires! It is also energetically inefficient.






